文法圧縮入門 #アルゴリズム

この記事は，「文字列アルゴリズム Advent Calendar 2017」12日目の記事です．

はじめに

今日は文字列を圧縮してみます．

P e t e r _ p i p e r _ p i c k e d _ a _ p e c k _ o f _ p i c k l e d _ p e p p e r s . _ A _ p e c k _ o f _ p i c k l e d _ p e p p e r s _ P e t e r _ P i p e r _ p i c k e d . _ I f _ P e t e r _ P i p e r _ p i c k e d _ a _ p e c k _ o f _ p i c k l e d _ p e p p e r s , _ W h e r e ' s _ t h e _ p e c k _ o f _ p i c k l e d _ p e p p e r s _ P e t e r _ P i p e r _ p i c k e d ?

この記事を最後のほうまで読むと，上記の早口言葉（196文字¹）が

P e t r _ p i c k d a o f l s . A I , W h ' ? | 04 05 01 03 07 08 24 06 01 09 24 01 05 25 27 26 04 00 01 02 11 12 26 04 13 28 29 05 30 14 31 28 33 25 34 31 29 35 36 37 30 39 42 41 43 38 45 46 32 06 32 40 48 44 49 50 15 04 04 10 47 51 53 47 | 00 40 27 44 55 52 16 54 52 17 12 51 55 18 04 19 20 25 01 21 04 02 20 01 54 22

のように圧縮されて短くなり（115文字²），さらに早く言えるようになります．

圧縮の技術は，まず 可逆圧縮 と 非可逆圧縮 に大別されます．
可逆圧縮とは，圧縮したものを展開（復元）すると，完全にデータが元通りになるような圧縮方法です．
一方非可逆圧縮では，圧縮したものを展開してもデータは完全に元通りにはなりません．この方法は，圧縮の際にいくらか情報を捨てることで，代わりに高い圧縮率を達成することができるもので，画像や音声の圧縮によく使われます．情報がいくらか失われても（≒画質や音質がいくらか劣化しても）人間が知覚する上で大した影響はないから，それよりも圧縮率を優先しよう，ということですね．

今回紹介するような文字列データ圧縮では，ふつう可逆圧縮を考えます（展開して得られたメッセージの文字がところどころ抜けていたりしたらキレそうになります）．以降，圧縮と言ったらすべて可逆圧縮ということにします．この記事では，文字列データ圧縮の中でも特に有名で，近年盛んに研究されている「文法圧縮³」という技術に入門してみたいと思います．

文法圧縮

データ圧縮の概説

さっそく圧縮していきたいところですが，まずはデータ圧縮についてもう少し知る必要があります．
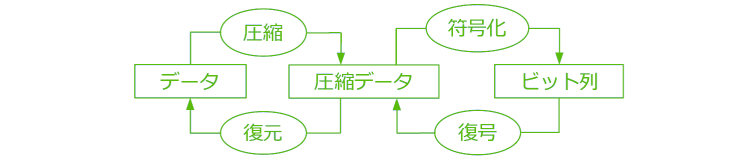
一般的なデータ圧縮・展開の仕組みを下図に示します．

圧縮と展開は以下のようにして行います．

圧縮
1. 元データ（文字列）を，圧縮データと呼ばれるものに変換します（圧縮）．圧縮と言ったとき，この操作だけを指すこともあります．
2. 圧縮データをビット列に変換します（符号化）．得られたビット列のサイズが元データを表現しているビット列のサイズより小さくなっていれば，圧縮成功です．
展開
1. ビット列から圧縮データを取り出します（復号）．
2. 圧縮データから元データを取り出します（復元）．

圧縮データとしてどのようなモデルを用いるか，というところに，その圧縮方法の最大の特徴があります．文法圧縮は，圧縮データとして 文脈自由文法 を構築する圧縮方法です．

今回は入門というタイトルなので，圧縮データの符号化・復号の部分は詳しく扱いません．しかし予想として，圧縮データを表す文字数が少なければ少ないほど，符号化したときのビット列のサイズも小さくなっていそうです⁴．つまり圧縮率を高めたいと思ったら，できるだけ少ない文字数で表せるような圧縮データ（すなわち文脈自由文法）の構築について考えることになりそうです．

文脈自由文法

$V$ を変数の有限集合， $\Sigma$ を終端記号の有限集合，$R$ を規則と呼ばれる $V$ から $(V \cup \Sigma)^{*}$ への関係の集合，$s$ を開始記号と呼ばれる特別な変数としたとき，$G = \{V,~\Sigma,~s,~R\}$ を文脈自由文法と言います．

【例】
$G = \{V,~\Sigma,~s,~R\}$，
$V = \{s,~x,~y,~z\}$，$\Sigma = \{{\rm a},~{\rm b},~{\rm c}\}$，
$R = \{s \rightarrow x~y,~x \rightarrow {\rm a}~z,~y \rightarrow {\rm a}~y~{\rm b},~y \rightarrow {\rm c},~z \rightarrow {\rm a~b} \}$．

文脈自由文法では，開始記号からはじめて順次規則を適用していくと，文脈自由言語という形式言語クラスに属する言語（≒文字列）が生成されます．実際に上の例から生成してみると，

まず，$s \rightarrow x~y$ より，$x~y$ が生成される．
$x$ と $y$ は共に変数だが，ひとまず $x$ の規則を考えてみると， $x \rightarrow {\rm a}~z$ より ${\rm a}~z~y$ が生成される．
$z \rightarrow {\rm a~b}$ より，${\rm a~a~b}~y$ となる．
残る変数は $y$ だが，$y$ については $y \rightarrow {\rm a}~y~{\rm b}$ と $y \rightarrow {\rm c}$ の2つの規則がある．前者は何度でも適用でき，後者が適用されるとそこで終わることから， ${\rm a}^n~{\rm c~b}^n ~~(n \in \mathbb{N})$ ⁵と得られる．したがって全体として，${\rm a~a~b~a}^n~{\rm c~b}^n$ が生成される．

となります．

文法圧縮では圧縮データとして「元データの文字列を生成するような文脈自由文法」を構築します．しかし上記のままの定義を採用すると，多少不都合（上の例で見たように，生成される文字列に $n$ のような変数が発生すると文字列が一意に定まらなくなり，元データを復元できません）があるため，もう少し制約を強めた定義を用います．すなわち，文法圧縮で使う文脈自由文法では，$\Sigma$ を元データの文字列に含まれるすべての文字（記号）から成る有限集合， $V$ を変数の有限全順序集合，$s$ を $V$ の最大元，規則の形を

$v \rightarrow a~~(v \in V, a \in \Sigma)$
$v_i \rightarrow v_{j_1}~v_{j_2} \cdots ~v_{j_n} ~~(v \in V,~i,j,n \in \mathbb{N},~v_i > v_j)$

のいずれか，かつある変数についてそれを左辺に持つ規則は $R$ 中にただ1つであるように限定します．
何やら難しそうですが，要は「ループしないような変数のおきかえルール集」だと思ってもらえれば大丈夫です．

文法サイズ

圧縮ではデータサイズを小さくしたいので，圧縮データは小さければ小さいほど良さそうです⁶．文法圧縮における圧縮データのサイズとは，構築された文脈自由文法のサイズ（文法サイズ）です．一般に文法サイズは，

規則の右辺（矢印の行き先）の終端記号および変数の個数の総和

で数えます⁷．その理由は，明示的に文字列として保持しておく情報がだいたいそれくらいで十分だからです．いま $V$ は全順序集合なので，左辺の変数が $V$ 中で $i$ 番目であるような規則の右辺を，配列の $i$ 番目に格納しておけばいいわけです．

【例】
文字列 ${\rm a~g~c~t~g~t~c~c~a~g~c~t~g~g~c~t~g~a~g~c~t~a~g~c~t}$ を生成する文脈自由文法として，

$G = \{V,~\Sigma,~s,~R\}$，
$V = \{0,~1,~2,~3,~4,~5,~6,~7,~8,~9,~10\}$，$\Sigma = \{{\rm a},~{\rm g},~{\rm c},~{\rm t}\}$，$s = 10$，
$R = \{$$0 \rightarrow {\rm a},$ $1 \rightarrow {\rm g},$ $2 \rightarrow {\rm c},$ $3 \rightarrow {\rm t},$ $4 \rightarrow 1~2~3,$ $5 \rightarrow 2~2,$ $6 \rightarrow 0~4~1,$ $7 \rightarrow 0~4,$ $8 \rightarrow 6~4~1~7,$ $9 \rightarrow 7~3~5,$ $10 \rightarrow 9~8~7$ $\}$

なる $G$ が考えられます（元の文字列，導出できましたか？）．これは，
$$[~{\rm a},~{\rm g},~{\rm c},~{\rm t},~1~2~3,~2~2,~0~4~1,~0~4,~6~4~1~7,~7~3~5,~9~8~7~]$$

のように配列に格納しておけば復元することができます（いま，変数は $V$ 中での順位に対応しており，変数 $v$ を左辺とする規則の右辺が配列の $v$ 番目に入っている）．この文法サイズは24です．

上の例の文字列に関して，これよりもサイズの小さい文脈自由文法を作ることはできるでしょうか？　答えはYESです（やってみてください）．文法圧縮のアルゴリズムは，文字列を入力として，その文字列を生成するようなできるだけサイズの小さい文脈自由文法を出力します．なぜサイズ最小を攻めないのかと不審に思われるかもしれませんが，そのような問題（入力文字列に対しそれを生成するようなサイズ最小の文脈自由文法を構築する問題）は 最小文法問題 と呼ばれ，決定問題がNP完全であることが知られています⁸．

RePair

せっかくなので，文法圧縮のアルゴリズムをひとつ紹介したいと思います．RePair⁹ はわかりやすくて圧縮率も高い文法圧縮アルゴリズムです．代償として，他の手法と比べると必要な作業領域や時間計算量が大きいという欠点があります．

アルゴリズムの概要

文字列中の（distinctな）隣り合う2文字の組をbigramと言います．たとえば文字列 abracadabra では，ab, br, ra, ac, ca, ad, da がbigramです．
RePairでは最初に各文字（終端記号）を変数に置換したあと，文字列中で最も出現頻度の高いbigramを変数に置換し，その変換を規則に追加します．いまbigramが変数に置換されてできた新たな文字列に対して，また同様に最も出現頻度の高いbigramを変数に置換，規則に追加します．これを繰り返していき，すべてのbigramの出現頻度が1になったらその文字列自身を変数に置換，規則に追加して終了します¹⁰．

【例】

簡単ですね．ここでは，頻度が同じbigramが複数あった場合，最初の出現がより先頭に近いほうを優先して置換しています．
ところで，さきほどは文法を文字列の配列として保持していましたが，RePairで構築した文法はもっと単純に，ひとつの文字列として保存することができます．RePairでは，作った $G=\{V,~\Sigma,~s,~R\}$ の規則 $R$ は，

はじめの $|\Sigma|$ 個が $v\rightarrow a~~(v \in V,~a \in \Sigma)$，
残りのうち $|R|-1$ 個目までが $v_i\rightarrow v_{j_1}~v_{j_2}~~(v \in V,~i,j\in \mathbb{N})$，
最後のものが $s\rightarrow v_{i_1}~v_{i_2} \cdots ~v_{i_n}~~(v \in V,~i,n\in \mathbb{N})$

というように，3つの区間でそれぞれどのような形であるかがわかっています．したがって，これらの区間の境界に区切りの記号を挟んでおけば，あとは並んだ $a \in \Sigma$ と $v \in V$ の列（すなわち文字列）から，各規則を知ることができます．
たとえば上の例（図）で構築した文法の配列は

$$[~{\rm a},~{\rm g},~{\rm c},~{\rm t},~1~2,~4~3,~0~5,~6~1,~7~3~2~2~7~5~1~6~6~]\\
\text{↓}\\
{\rm a}~{\rm g}~{\rm c}~{\rm t}~|~1~2~4~3~0~5~6~1~|~7~3~2~2~7~5~1~6~6$$

のように文字列で表現できます．元の文字列25文字に比べ，圧縮後は文法サイズが21，圧縮データを表す文字列は23文字となり，無事圧縮されました．
もうお気づきかもしれませんが，この記事の冒頭にあった茶番では，早口言葉をRePairで圧縮しています．これでめでたく，早口言葉をさらに早く言えるようになりました．

線形時間RePair（予告）

RePairの時間計算量はどれくらいでしょうか．
愚直に行うと，入力文字列の長さ $n$ に対し，そのときのすべてのbigramの出現頻度を数えあげるのに $O(n)$ 時間，最頻出のものを変数に置き換えるのに $O(n)$ 時間（これら合わせて $O(n)$ 時間），それらが実行されるステップ数（$=O(n)$）回あるので，全体で $O(n^2)$ 時間という見積もりになりそうです．
$O(n^2)$ 時間というと（少なくとも筆者の知る文字列の界隈では）あまりいい顔をされないのが実情です．しかしながら，RePairは巧緻な工夫を凝らすことによって $O(n)$ 時間計算量を達成することができます¹¹．さっそく紹介していきたいところですが，この内容は入門の域を甚だ逸脱するので（記事の分量も多くなってきましたし），次々回「文字列アルゴリズム Advent Calendar 2017」14日目の記事として書くことにしたいと思います（書きました）．

おわりに

今日は文法圧縮に入門しました．
この記事の要点は以下の通りです．

文法圧縮という文字列データの可逆圧縮の技術が存在する．
文法圧縮は，圧縮データとして「元の文字列を生成するようなサイズの小さい文脈自由文法」を構築する圧縮方法である．
RePairは最頻出のbigramを置換していく文法圧縮アルゴリズムである．

お疲れさまでした．
誤字・脱字，内容の間違いなどありましたらご指摘いただけると幸いです．

文字の境界を強調するため，文字と文字の区切りに空白を入れています（空白は文字数に入っていません）．直後の圧縮後の文字列に関しても同様です．以降でも必要に応じて文字の区切りに空白を入れています． ↩
2桁の整数で書かれているものは一文字として数えています．これは，実際にはこれらの整数は変数として，ひとつの文字と同等に扱われるためです． ↩
John C. Kieffer and En-hui Yang, “Grammar-based codes: A new class of universal lossless source codes”, IEEE Transactions on Information Theory, 46(3):737–754, 2000. ↩
各文字すべてに同じ長さのビット列を割り当てるような符号化では，この予想はほぼ正しいです．ですがより効率よく（≒より短く）符号化しようとした場合には，出現する文字の種類数や頻度なども考慮するため，一概に文字数だけに比例するとは言い切れません．しかしいずれにせよ，圧縮データが元データより少ない文字数で表せるのであれば，符号化したときに元データを表すビット列よりもサイズが大きくなってしまうようなことはまずありません．文字列の符号化の話，誰か書いてくれないかな……． ↩
$x$ を文字列，$i$ を自然数としたとき，$x^i$ は $x$ を $i$ 回繰り返した文字列を表します． ↩
実際には，単純に圧縮率さえ良ければ正義，というわけにはいかないようです．圧縮・展開に必要な作業領域や時間計算量，圧縮された状態のデータに対して行える各種の操作（検索や部分展開など）といった諸々も含めて，その圧縮技術への評価が決まります． ↩
文脈自由文法の規則数を文法サイズとする定義もあります．これは，任意の文脈自由文法が等価なチョムスキー標準形に変換可能であり，その際文法サイズは規則数に対して定数個しか変化しないことに由来します． ↩
Moses Charikar, Eric Lehman, Ding Liu, Rina Panigrahy, Manoj Prabhakaran, Amit Sahai, and abhi shelat, "The smallest grammar problem", IEEE Transactions on Information Theory, 51(7):2554-2576, 2005. ↩
N.Jesper Larsson and Alistair Moffat, "Off-line dictionary-based compression", Proceedings of the IEEE, 88(11):1722-1732, 2000. ↩
最後の文字列自身の変数への置換は，論文中には明記されていません．しかし説明の整合性の観点から，ここでは置換するものとしています．この操作はしてもしなくても，圧縮データを表現する文字列（配列）は結局同じものになります． ↩
それでも，他の文法圧縮に比べて（実験的な）実行時間は遅いようです……． ↩