機械学習に必要な高校数学やり直しアドベントカレンダー Advent Calendar 2016の11日目の記事です。10日目はyajuさんで線形回帰で二乗和を2で割る理由についてでした。
はじめに
難しいとよく言われる微分ですが、そんなに難しい概念ではないですし、とても便利な武器になるんですよ!という記事です。
変化率
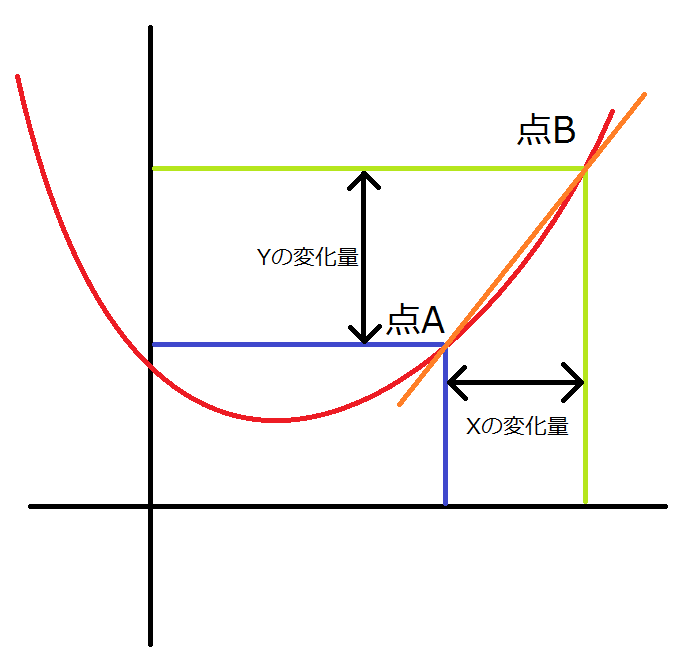
まず、最初に変化率という概念について考えてみます。点aから点bへ変化するとき変化率は (yの変化量)/(xの変化量) 、すなわち
$$ \frac{By-Ay}{Bx-Ax} $$
と表せます。このように2点間でxの変化量に対するyの変化量の割合を変化率と呼び、点A,Bを通る直線を引いたときの傾きと等しい値となります。
1点の変化率
2点間の距離を小さくしていくことを考えていきます。点Bを点Aに近づけていくことで1点での変化率に近づけていくことができます。この1点での変化率、これこそが微分で求めているものです。この値はこの1点のみを通る線(接線)の傾きと等しい値です。
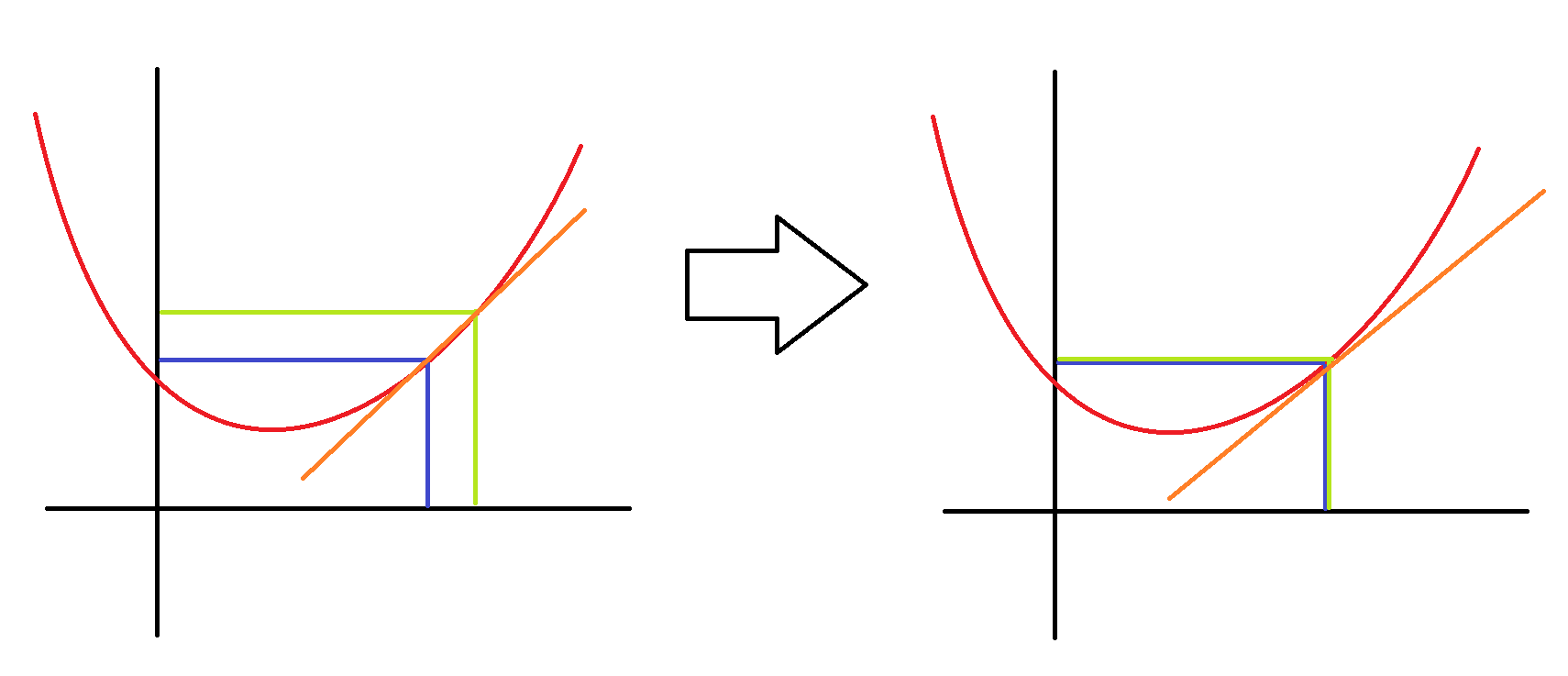
この距離を0に近づけていくことを数学では極限を用いて、以下の式で記述することができます。
$$ \lim_{x \to 0} \frac{f(x+h)-f(x)}{h} $$
三角関数、逆関数、合成関数などの微分のような複雑な数式であってもやっていることは同じで、変化率を求めているだけです!
微分でわかること
微分が何を表しているのかわかったところで微分が何の役に立つのか見ていきます。
極大・極小
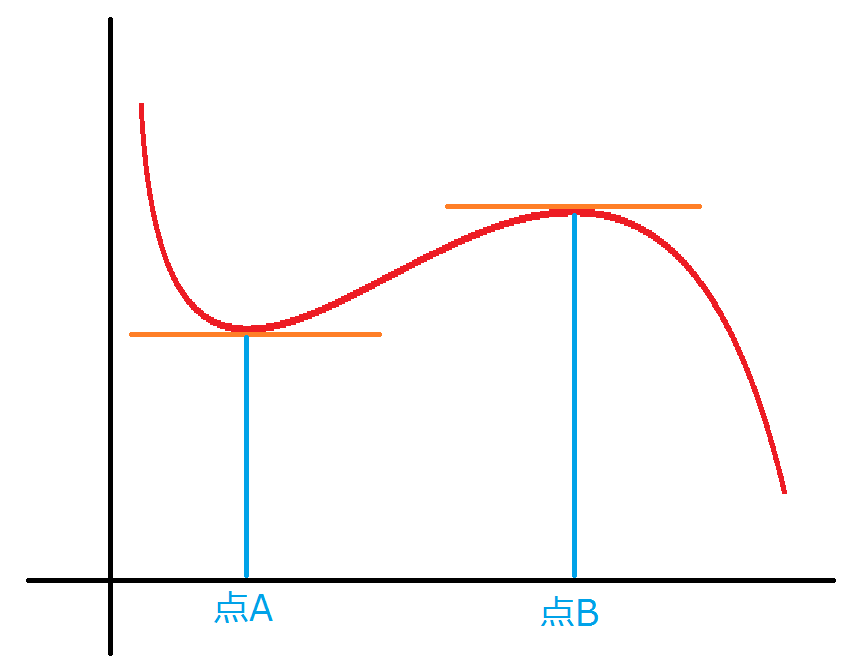
微分した値が0になる点について考えてみます。変化率が0となる点は以下のグラフのように接線がx軸と平行になる点です。この点では局地的に最も大きい値(点B, 極大値)、もしくは最も小さい値(点A, 極小値)となります。微分を行うことでグラフ内の極大値、極小値を求めることができます!
勾配降下法
機械学習では関数(二乗誤差関数、交差エントロピーなど)の最小化を考えることがあります。その際に微分で極小値を求める方法を応用した方法を用います。それが勾配降下法です。
関数$ E(w) $の最小値について考えます。以下の式を繰り返し適用することで$ E(w) $がもっとも小さくなる$w$を求める事ができます。
$$ w^{t+1} = w^t - \epsilon\frac{dE}{dw}$$
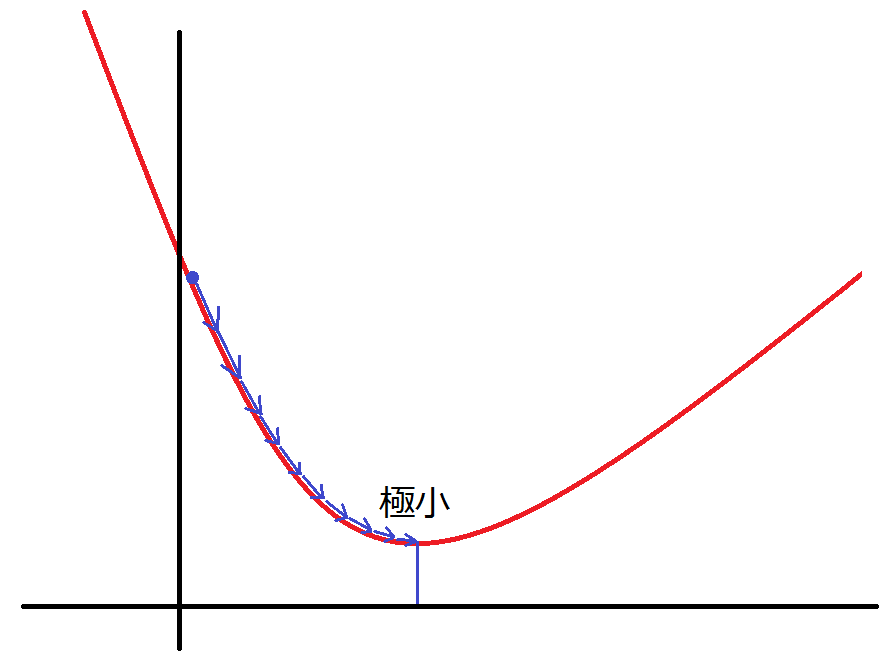
$\frac{dE}{dw}$は微分を表す記号で関数$E(w)$の傾きを表します。この式をグラフで表すと、極小となる点の方向に$w$が移動します。極小となる点に近づくにしたがって微分した値(傾き)は小さくなっているので、移動する量は徐々に少なくなっていきます。微分した値(傾き)が0となる点(極小)で移動は終わり極小となる点$w$を求めることができます。
おわりに
このように微分は非常に便利で役に立つ武器となります。
明日は機械学習に必要な高校数学やり直しアドベントカレンダー Advent Calendar 2016の12日目、clown0082さんの記事です!