グラフィカルな探索的データ解析
高度な統計的推論を行う前に、まずデータをプロットし、簡単な要約統計を計算することで、データを探索する必要があります。
探索的データ解析(EDA : Exploratory Data Analysis)と呼ばれるこのプロセスは、データの統計的分析の重要な第一歩です。
"You can observe a lot by watching."
-- Yogi Berra
"Exploratory data analysis can never be the whole story, but nothing else can serve as the foundation stone."
-- A book entitled Exploratory Data Analysis in 1977 by John Tukey
経験的累積分布関数(eCDF)
累積分布関数とは「確率変数Xがある値x以下(X <= x)の値となる確率」を表す関数です。

累積分布関数とはから引用
経験的累積分布関数(eCDF : empirical Cumulative Distribution Function)とは、
未知の確率分布に従って生成されたn個のデータ(標本)を用いて、この未知の確率分布の累積分布関数を推定したものです。
n個のデータポイントのそれぞれで1/nずつジャンプアップするステップ関数です。
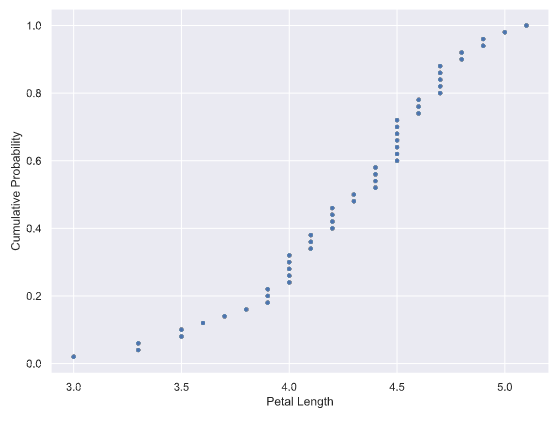
上の図の横軸は花ぴらの長さ(標本データ)、縦軸が累積分布になります。
花ぴらの長さの標本データは下記とします。
array([4.7, 4.5, 4.9, 4. , 4.6, 4.5, 4.7, 3.3, 4.6, 3.9, 3.5, 4.2, 4. ,
4.7, 3.6, 4.4, 4.5, 4.1, 4.5, 3.9, 4.8, 4. , 4.9, 4.7, 4.3, 4.4,
4.8, 5. , 4.5, 3.5, 3.8, 3.7, 3.9, 5.1, 4.5, 4.5, 4.7, 4.4, 4.1,
4. , 4.4, 4.6, 4. , 3.3, 4.2, 4.2, 4.2, 4.3, 3. , 4.1])
ecdf関数を作成します。
def ecdf(data):
# Number of data points: n
n = len(data)
# x-data for the ECDF: x
x = np.sort(data)
# y-data for the ECDF: y
y = np.arange(1, n+1) / n
return x, y
ecdf関数を用いて標本データを処理します。
x, y = ecdf(petal_length)
処理結果のx, yは下記になります。
# x
array([3. , 3.3, 3.3, 3.5, 3.5, 3.6, 3.7, 3.8, 3.9, 3.9, 3.9, 4. , 4. ,
4. , 4. , 4. , 4.1, 4.1, 4.1, 4.2, 4.2, 4.2, 4.2, 4.3, 4.3, 4.4,
4.4, 4.4, 4.4, 4.5, 4.5, 4.5, 4.5, 4.5, 4.5, 4.5, 4.6, 4.6, 4.6,
4.7, 4.7, 4.7, 4.7, 4.7, 4.8, 4.8, 4.9, 4.9, 5. , 5.1])
# y
array([0.02, 0.04, 0.06, 0.08, 0.1 , 0.12, 0.14, 0.16, 0.18, 0.2 , 0.22,
0.24, 0.26, 0.28, 0.3 , 0.32, 0.34, 0.36, 0.38, 0.4 , 0.42, 0.44,
0.46, 0.48, 0.5 , 0.52, 0.54, 0.56, 0.58, 0.6 , 0.62, 0.64, 0.66,
0.68, 0.7 , 0.72, 0.74, 0.76, 0.78, 0.8 , 0.82, 0.84, 0.86, 0.88,
0.9 , 0.92, 0.94, 0.96, 0.98, 1. ])
x, yをプロットします。
plt.plot(x, y, marker='.', linestyle='none')
plt.xlabel('Petal Length')
plt.ylabel('Cumulative Probability')
plt.show()
定量的な探索的データ解析
データセットの顕著な特徴をいくつかの数値で簡潔に表すことができる、有用な要約統計量を計算します。
平均値と中央値
平均値は簡単に計算できる要約統計量ですが、外れ値による影響が大きい。
np.mean(petal_length)
# 4.26
中央値は、データをソートし中央にあるデータを選択します。外れ値による影響がない。
np.median(petal_length)
# 4.35
パーセンタイル値と外れ値
パーセンタイル(Percentile)は、データを小さい順にソートしたとき、初めから数えて全体のx%に位置する値をxパーセンタイルといいます。
25パーセンタイルであれば、最小値から数えて25%に位置する値を指します。
中央値は、50パーセンタイルの別名です。
percentiles = np.array([2.5, 25, 50, 75, 97.5])
np.percentile(petal_length, percentiles)
# [3.3 4. 4.35 4.6 4.9775]
外れ値(Outlier)は、他の値から大きく外れた値のことです。
ここで重要なのは、外れ値は必ずしも誤ったデータポイントではないということです。
何らかの理由がない限り、外れ値が誤っていると決めつけてはいけません。
箱ひげ図を用いて、最大値最小値に加えて、「四分位数」(25パーセンタイル、50パーセンタイル、75パーセンタイル)の確認が可能です。
分散と標準偏差
分散(variance)は、分布の広がりを表す統計量で、各データと平均値の差を2乗したものの平均です。
標準偏差の2乗に等しい。
# 各データと平均値の差
differences = petal_length - np.mean(petal_length)
# 2乗して
diff_sq = np.square(differences)
# 平均
variance = np.mean(diff_sq)
# variance : 0.21640000000000004
# またはnp.varで計算
variance = np.var(petal_length)
# variance : 0.21640000000000004
標準偏差(Standard Deviation)は分散の平方根です。
# 分散の平方根
np.sqrt(variance)
# 0.4651881339845203
# np.stdで計算
np.std(petal_length)
# 0.4651881339845203
共分散とピアソン相関係数
共分散(Covariance)は、2つの変数の関係性を見るための指標で、2組の変数の偏差の積の平均です。
共分散はnumpyのcov関数で求められます。
np.cov(x, y)
結果として共分散マトリックスが出力されます。
[[0.22081633 0.07310204]
[0.07310204 0.03910612]]
共分散マトリックスの見方
- xとyの共分散:(1,2)と(2,1)の要素です。上記の例の0.07310204です。
- xの分散:(1,1)の要素です。
- yの分散:(2,2)の要素です。
共分散の定義式から、各変数のスケールや単位に依存してしまいます。
スケールの影響を受けずに、2つの変数の関係を数値化するのがピアソン相関係数(Pearson Correlation Coefficient)です。
相関係数は、-1から1までの値を取り、1に近ければ近いほど正の相関があるといい、-1に近ければ近いほど負の相関があるといいます。
0に近い場合は、無相関であるといいます。
相関係数はnumpyのcorrcoef関数で求められます。
np.corrcoef(x, y)
結果として相関係数マトリックスが出力されます。
[[1. 0.78666809]
[0.78666809 1. ]]
相関係数マトリックスの見方
- xとyの相関係数:(1,2)と(2,1)の要素です。上記の例の0.07310204です。
- x自分自身の相関係数:(1,1)の要素です。(1固定)
- y自分自身の相関係数:(2,2)の要素です。(1固定)
確率的思考-離散変数
統計的な推論は確率に基づいて行われます。
データから絶対的な確信を持って意味のあることを言えることはほとんどないので、
データに関する定量的な記述には確率的な言葉を使います。
離散的な量、つまり整数のように特定の値しか取れない量について、確率的に考えます。
確率論理と統計的推論
確率論理(Probabilistic Logic)は、確率論と演繹論理を組み合わせて不確実性を取り扱う学問です。
統計的推論(Statistical Inference)は、実験や調査によって得られたデータを用いて、
そのデータの背後に想定される母集団の特性について推論することです。
統計的推論の目的は、
- 同じデータをもう一度集めたらどうなるか、確率的な結論を出すこと
- データから実用的な結論を出すこと
- 比較的少ないデータや観察結果から、より一般的な結論を導き出すこと
乱数生成器とハッカー統計
ハッカー統計(Hacker Statistics)は、データを何度も繰り返して取得する代わりに、
Pythonの乱数生成器などを使用し、繰り返される測定をシミュレーションすることです。
二項分布
結果が2つしかない試行をベルヌーイ試行といいます。(コインを投げたときに表が出るか裏が出るか)
ベルヌーイ試行をn回行って、成功する回数が従う確率分布を二項分布(Binomial Distribution)といいます。
二項分布はnumpyのrandom.binomialで計算できます。
binomialに渡すパラメータは、試行回数(n)、成功する確率(p)、サンプル数です。
# 確率1/2で表が出るコインを1000回投げて、表が出る回数を求める。5回繰り返してサンプル取得する。
np.random.binomial(1000, 0.5, 5)
# [495 500 482 505 510]
ポアソン分布
ポアソン分布(Poisson Distribution)は、ある期間に平均λ回起こる現象が、ある期間にX回起きる確率の分布です。
稀な事象が起きる確率のときに使用します。例えば、単位面積当たりの雨粒の数や、1平米当たりの木の数などがポアソン分布に従います。
ポアソン分布はnumpyのrandom.poissonで計算できます。
# 単位面積当たりの雨粒の平均が7の場合、単位面積当たりの雨粒の数を求める。5回繰り返してサンプル取得する。
np.random.poisson(7, 5)
# [10 5 12 4 4]
確率的思考-連続変数
任意の分数値を取ることができるような連続変数は、離散変数の原理の多くは同じですが、
いくつか違いがあります。
確率密度関数
確率密度関数(PDF : Probability Density Function)は、連続変数のある値を観測する確率を表します。
確率密度関数は、確率質量関数(PMF : Probability Mass Function)の連続的なアナログです。
正規分布
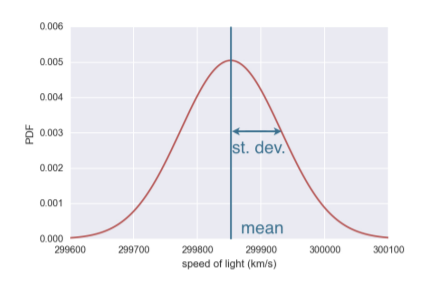
正規分布(Normal Distribution)はガウス分布ともいわれ、代表的な連続型の確率分布です。
正規分布のPDFは対称で、ピークが1つだけあります。
正規分布はnumpyのrandom.normalで計算できます。
normalに渡すパラメータは、平均値、標準偏差、サンプル数です。
# 平均値が5, 標準偏差が10の場合、取り得る数を求める。5回繰り返してサンプル取得する。
np.random.normal(5, 10, 5)
# [-6.70904325 12.66075469 3.29902045 -5.30994418 6.23031126]
サンプルデータから推測したい場合は以下で行えます。
mean = np.mean(sample_data)
std = np.std(sample_data)
np.random.normal(mean, std, size=10000)
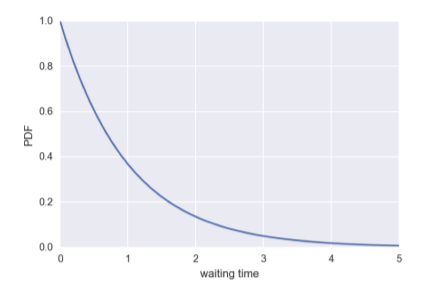
指数分布
指数分布(Exponential Distribution)は、連続型確率分布の一つで、機械が故障してから次に故障するまでの期間や、災害が起こってから次に起こるまでの期間のように、次に何かが起こるまでの期間が従う分布です。
指数分布はnumpyのrandom.exponentialで計算できます。
mean = np.mean(sample_times)
np.random.exponential(mean, size=10000)
最適化によるパラメータ推定
統計的推論を行う際には、確率という言葉を使用します。データを記述する確率分布にはパラメータがあります。
統計的推論の主な目的は、これらのパラメータ値を推定することです。
これにより、データを簡潔かつ明確に記述し、そこから結論を導き出すことができます。
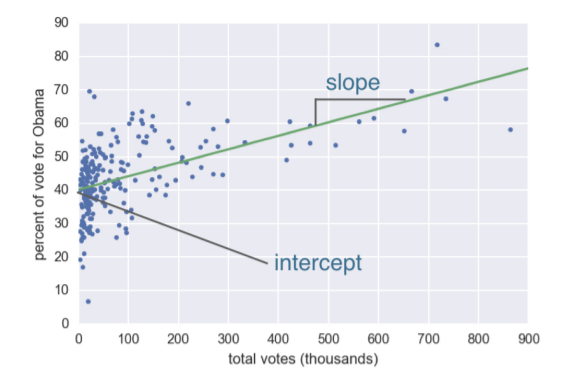
最小二乗法
データポイントと線との距離を残差(Residual)といいます。
最小二乗法(Least Squares)は、残差の二乗和が最小となるようなパラメータを見つけることです。
最小二乗法はnumpyのpolyfit関数で求められます。
slope, intercept = np.polyfit(data_x, data_y, 1)
パラメータの3つ目は1次式を指定しています。
1次式指定の戻り値は、傾きと切片になります。
2次式なども行えます。Numpy.polyfit を使ったカーブフィッティングを参考してください。
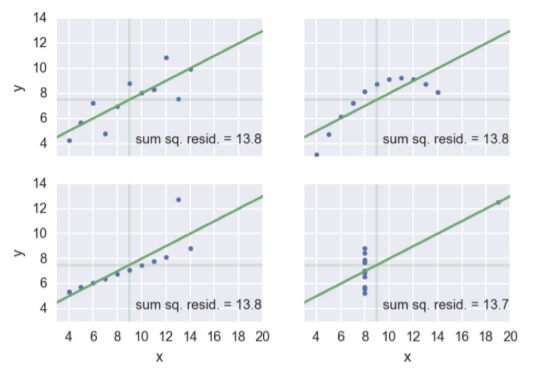
アンスコムの数値例
アンスコムの数値例(Anscombe's quartet)とは、回帰分析において、散布図はそれぞれ異なるのに回帰直線やその他の統計量が同じになってしまう現象です。
回帰分析をする前に散布図を確認し傾向を把握することの重要性を示します。
ブートストラップ法と信頼区間
"pull oneself up by your bootstraps "とは、困難な課題を誰の助けも借りずに自力で達成することを意味する古典的な慣用句です。
統計的推論では、データ取得を無限回繰り返したらどうなるかを知りたいと思います。
これは不可能なことですが、実際にあるデータだけを使って、無限回の実験と同じ結果に近づけることができるでしょうか?
答えは「YES」です。そのための技術がブートストラップ法(Bootstrap)です。
リサンプリングはnumpyのrandom.choiceで求められます。
sample = np.random.choice([1,2,3,4,5], size=5)
# [5, 3, 5, 5, 2])
測定を何度も繰り返した場合、観測された値のp%がp%信頼区間内に収まります。
信頼区間は以下のように計算できます。
np.percentile(replicates, [2.7, 97.5])
# [ 299837., 299868.]
仮説検定
モデルのパラメータを定義し、推定する方法がわかりました。
しかし、モデルが真である場合、データを観察することはどのくらい妥当なのかという疑問が残ります。
この疑問を解決するのが仮説検定です。
P値
統計的仮説検定において、帰無仮説の下(もと)での検定統計量を求め,その値よりも極端な値をとる確率のこと。
帰無仮説が正しいと仮定した場合,P値が小さいほど、検定統計量がそのような極端な値をとることはあまり起こりえないことを意味します。そこで,帰無仮説を否定した対立仮説の方が正しいのではないかと判断します。(P値が大きい場合は,帰無仮説の下ではそのようなことはよく起きることなので,帰無仮説を受け入れます)。
一般的にP値が5%または1%以下の場合に帰無仮説を偽として棄却し、対立仮説を採択します。
A/Bテスト
ABテストとは2つのものを比較するテストです。 「AパターンとBパターンではどちらがよいか」を比べます。
インターネットマーケティングでよく行われる手法で、サイトや広告のアクセス数や成約率などのデータを比較し、成果が出ているほうを採用します。