$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
\def\ketround#1{\mathinner{\left|{,#1,}\right)}}
$$
2018年は主に量子アニーリングについて調べ、シミュレータを使いながら学習を進めていました。2019年は量子ゲートについても勉強してみようと決心し、Qiitaの記事を読んでみたりシミュレータを動かし始めたりしています。
2019.02.11 制御トフォリゲートの量子回路図に誤りがあったため訂正しました。
はじめに
量子ゲートはユニタリ演算子で表現することができます。例えばNOTゲート($X$)やアダマールゲート($H$)は1量子ビットに作用します。また、量子もつれ状態を作る場合には2量子ビットに作用する制御NOTゲート($CNOT$)が必要になります。さらに、トフォリゲート($CCNOT$)1やフレドキンゲート2などの3量子ビットに作用するゲートもあります。
多量子ビットに作用するゲートは、制御ビットの値に応じて標的ビットへの作用が変わります。制御NOTゲートの場合、制御ビットが1の場合のみ標的ビットを反転します。3量子ビットに作用するトフォリゲートの場合には、2つの制御ビットがともに1の場合のみ、標的ビットを反転します。
複数のゲートを組み合わせて何らかの機能を実現しようとした場合に、機能に対応するゲート$U$を制御ゲートにしたいことがあります。例えば、ショアのアルゴリズムを実装する場合には、加算器としての機能を持つ制御ユニタリゲートが必要になります。このような回路を構成するにはどのように量子ゲートを組み合わせればよいのでしょうか?本記事ではトフォリゲートを例として、制御ゲートの構成方法について解説していきたいと思います。
準備
制御トフォリゲートを構成するために必要となる要素について解説します。
多量子ビット状態の表現
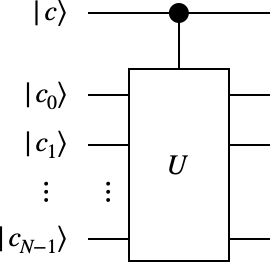
1量子ビット状態と多量子ビット状態を区別するために、1量子ビット状態を$\ket{*}$で、多量子ビット状態を$\left| * \right)$で表すことにします。すなわち、
\left| k \right) \equiv \ket{c_{0}} \otimes \ket{c_{1}} \otimes \cdots \otimes \ket{c_{N-1}}
, \quad k = 2^{0}c_{0} + 2^{1} c_{1} + \cdots + 2^{N-1}c_{N-1}
, \quad c_{i} \in \left\{ 0, 1 \right\}
です。
制御ゲート
制御ゲートは、制御ビットとが1のときのみ標的ビットに演算を施すゲートです。具体例として制御NOTゲートの作用を見てみましょう。
CNOT: \,\, \ket{x} \ket{y} \mapsto \ket{x} \ket{y \oplus x}.
$\ket{x}$が制御ビット、$\ket{y}$が標的ビットに対応しています。2量子ビットに対する演算なので、CNOTゲートは4×4行列で表現することができます。
CNOT = \left(
\begin{matrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
\end{matrix}
\right) = \left(
\begin{matrix}
I & O \\
O & X
\end{matrix}
\right).
ただし、$I$は2×2の恒等行列(単位行列)を、$X$はNOTゲートを表すものとします。$X$の部分を任意の1量子ビットに対するゲート、すなわち2×2ユニタリ行列で置き換えると、これは制御ユニタリ行列$CU$となります。
CU: \,\, \ket{x} \ket{y} \mapsto \left\{
\begin{matrix}
\ket{x} \ket{y}, &\quad x=0 \\
\ket{x} \left( U\ket{y} \right), &\quad x=1
\end{matrix}
\right. , \quad
CU = \left(
\begin{matrix}
I & O \\
O & U
\end{matrix}
\right).
標的が1ビットの場合、制御ユニタリゲートは任意のユニタリ行列を回転ゲートと位相ゲートの積で表現できることを利用し、制御NOTゲートと組み合わせることで実現できます3。一方で、先に例を挙げたショアのアルゴリズムを実装しようすると、制御加算器ゲートを用意する必要があり多量子ビットに作用する制御ゲートを構成しなければなりません。加算器は構成が少々複雑であるため、ここでは制御トフォリゲート(CCCNOTゲート)を実現する量子回路を作成します。
トフォリゲートは3量子ビットに作用し、2つの制御ビットがともに1のときに標的ビットを反転するゲートです。したがって、
CCNOT: \,\, \ket{x} \ket{y} \ket{z} \mapsto \ket{x} \ket{y} \ket{z \oplus xy}
です。これをさらに制御ゲート化するので、CCCNOTゲートは4量子ビット状態に対するゲートになります。すなわち、
CCCNOT: \,\, \ket{w} \ket{x} \ket{y} \ket{z} \mapsto \ket{w} \ket{x} \ket{y} \ket{z \oplus wxy}
を実現するゲートです。
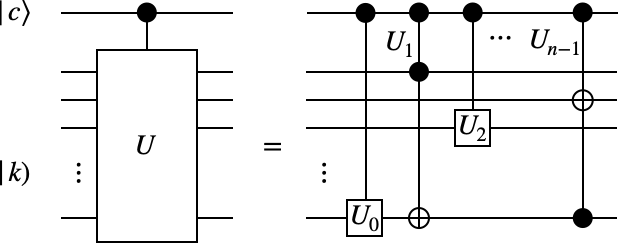
ゲートの分解
一般に、多量子ビットに作用するゲート$U$は、1量子ビットゲートと制御NOTゲートの組み合わせによって表現することができます4。$U_{i}$は1量子ビットゲートまたは制御NOTゲートを表すものとします。下図は$U_{1}$と$U_{n-1}$として制御NOTゲートを選択した場合の例です。
U = U_{n-1} U_{n-2} \cdots U_{2} U_{1} U_{0}.
任意のゲート演算を実現するために必要なゲートセットをユニバーサルゲートセットと呼びます。詳しくはユニバーサル量子コンピュータの「ユニバーサル」について解説で丁寧に解説されています。
さて、多量子ビットゲート$U$を制御ゲート化するためにはどうすればよいでしょうか。単純に考えればよく、$U$を複数のゲートに分解できることを利用し、分解後のゲートをそれぞれ制御ゲートで置き換えればよいことが分かります。標的ビット$\ket{c}$が1の場合のみ$U_{0}, U_{1}, \cdots , U_{n-1}$が$\left| k \right)$に作用するため、制御ゲートになっています。したがって、$U$を構成する各ゲート(すなわちユニバーサルゲートセット)に対応する制御ゲートを構成できれば、任意のゲートに対応する制御ゲートを構成することができます。
制御トフォリゲート
制御トフォリゲートを構成していきます。
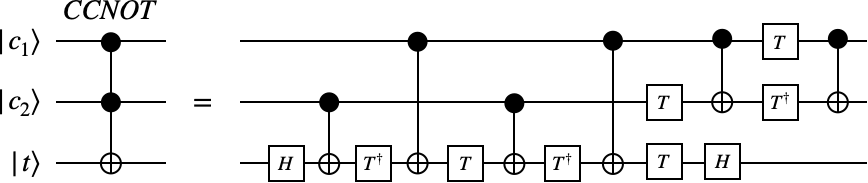
トフォリゲート
天下りになりますが、トフォリゲートは
- アダマールゲート
- 位相ゲート
- 制御NOTゲート
によって構成することができます。ただし、位相ゲート$P_{\phi}$は以下で定義されます。
P _{\phi} = \left(
\begin{matrix}
1 & 0 \\
0 & e^{i\phi}
\end{matrix}
\right).
実際には、
T=P_{\frac{\pi}{4}}, \quad
T^{\dagger} = P_{-\frac{\pi}{4}}
のみを使用します。上記ゲートを組み合わせて、トフォリゲートは以下のような回路で表現できます。
Blueqatで確認してみます。トフォリゲートをccx5で実行できるようにしました。引数control1およびcontrol2には制御ビットに対応する量子ビット番号を、targetには標的ビットに対応する量子ビット番号を渡します。
from blueqat import Circuit
import numpy as np
# The number of qubits
N=3
# Toffoli gate
def ccx(circuit, control1, control2, target):
circuit.h[target]
circuit.cx[control2,target]
circuit.rz(-np.pi/4)[target]
circuit.cx[control1,target]
circuit.rz(np.pi/4)[target]
circuit.cx[control2,target]
circuit.rz(-np.pi/4)[target]
circuit.cx[control1,target]
circuit.rz(np.pi/4)[control2]
circuit.rz(np.pi/4)[target]
circuit.cx[control1,control2]
circuit.h[target]
circuit.rz(np.pi/4)[control1]
circuit.rz(-np.pi/4)[control2]
circuit.cx[control1,control2]
return circuit
# Test
for k in range(2**N):
c=Circuit(N)
# bit
tmp = []
for shift in range(N-1, -1, -1):
tmp.append((k>>shift) & 0x01)
# X gate
for i, bit in enumerate(tmp):
if bit == 1:
c.x[i]
ret=ccx(c, 0, 1, 2).m[:].run(shots=100)
print("{}->{}".format(tmp, ret))
上記スクリプトを実行すると以下の結果を得ました。$c_{1} = c_{2} = 1$の場合のみ$\ket{t}$(左から3番目のビット)が反転していることが分かります。正しく動作しているようです。
[0, 0, 0]->Counter({'000': 100})
[0, 0, 1]->Counter({'001': 100})
[0, 1, 0]->Counter({'010': 100})
[0, 1, 1]->Counter({'011': 100})
[1, 0, 0]->Counter({'100': 100})
[1, 0, 1]->Counter({'101': 100})
[1, 1, 0]->Counter({'111': 100})
[1, 1, 1]->Counter({'110': 100})
トフォリゲートが$H$、$CNOT$、$T$および$T^{\dagger}$の組み合わせで実現できることが分かりました。したがって、制御トフォリゲートを記述するためには、以下を準備する必要があります。次節以降は、下記ゲートを構成する方法について記載します。
制御制御NOTゲート
制御$CNOT$ゲートは、定義から明らかなようにトフォリゲートです。
制御位相ゲート
こちらも天下りですが、以下のようにすれば制御位相ゲートを構成できます3。
制御アダマールゲート
アダマールゲートは、Xゲートと$y$軸回りの回転ゲートの積で表現できます。
H = XR_{y} (\pi /2) =
\left(
\begin{matrix}
0 & 1 \\
1 & 0
\end{matrix}
\right)
\left(
\begin{matrix}
\cos (\pi/4) & -\sin (\pi/4) \\
\sin (\pi/4) & \cos (\pi/4)
\end{matrix}
\right)
=
\frac{1}{\sqrt{2}}
\left(
\begin{matrix}
1 & 1 \\
1 & -1
\end{matrix}
\right)
と書けます。$y$軸周りの回転ゲートは制御ゲートを構成する際に必要になりますので、定義を確認しておきましょう。
y軸周りの回転ゲート
回転ゲートはパウリ行列を使って表現できます。$y$軸周りの場合には、$Y$ゲートを使って
R_{y} (2\theta) = e^{-i\theta Y}, \quad Y = \left(
\begin{matrix}
0 & -i \\
i & 0
\end{matrix}
\right)
と書けます。$Z$の固有状態を考えているため$Y$は対角行列ではありません。したがって、$Y$を対角化するか、あるいは指数関数の定義に従って展開する必要があります。後者の方法を採用すると、
\begin{align}
R_{y}(2\theta ) &\equiv e^{-i\theta Y} \\
&= \sum _{k=0} ^{\infty} \frac{(-i\theta ) ^{k}}{k!} Y^{k} \\
&= \sum _{l=0} ^{\infty} \frac{(-i\theta ) ^{2l}}{(2l)!} Y^{2l} +
\sum _{l=0} ^{\infty} \frac{(-i\theta ) ^{2l+1}}{(2l+1)!} Y^{2l+1} \\
&= \sum _{l=0} ^{\infty} \frac{(-1) ^{l}\theta ^{2l}}{(2l)!} I
- i\sum _{l=0} ^{\infty} \frac{(-1) ^{l} \theta ^{2l+1}}{(2l+1)!} Y \\
&= (\cos \theta )I - (i \sin \theta ) Y
\end{align}
を得ます。ただし、$Y^{2}=I$であることを利用しています。2×2行列で表現すると以下のようになります。
R_{y} (2\theta ) = \left(
\begin{matrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{matrix}
\right).
$y$軸周りの回転ゲートは、アダマールゲートを制御ゲート化する際に重要な役割を果たします。
制御回転ゲート
$y$軸周りの回転ゲートを制御ゲート化します。1量子ビットゲート$U$が以下のように分解できることを利用します3。
U(\phi, \alpha , \beta, \gamma) = R_{y} (\alpha ) R_{z} (\beta ) R_{y} (\gamma ).
$U$は3つの行列$A$、$B$、$C$とNOTゲートを使って以下のように書くことができます。
U(\phi, \alpha , \beta, \gamma) = e^{i\phi}AXBXC, \quad ABC=I
ただし、
A = -R_{y} \left( \frac{\alpha - \gamma}{2} \right) , \quad B = R_{y} \left( \frac{-\alpha + \gamma}{2} \right) R_{z} \left( -\frac{\beta}{2} \right), \quad
C = R_{z} \left( \frac{\beta}{2} \right) R_{y} (\gamma)
です。$\alpha = \theta /2$および$\beta = \gamma = 0$および$\phi = \pi$を選んだ場合、すなわち
A = R_{y} \left( \frac{\alpha}{2} \right), \quad B = R_{y} \left( -\frac{\alpha}{2} \right), \quad C=I
とすれば、
R_{y} (\theta ) = -AXBXC = -R_{y} \left( \frac{\alpha}{2} \right) X R_{y} \left( -\frac{\alpha}{2} \right) X
を満たします。係数-1は系全体にかかる位相であるため無視します。$ABC=I$を満たすので、制御ビットが1の場合のみ$X$が標的ビットに作用すれば制御ゲートになります。これは、NOTゲートを制御NOTゲートに置き換えることで実現できます。
制御アダマールゲートの構成
制御アダマールゲートを構成する要素がすべて揃ったので、これらを組み合わせます。制御アダマールゲートは、以下の量子回路図で実現できます。制御NOTゲートと制御回転ゲート(y軸周り)によって、制御アダマールゲートが実現できました。
正しく動作するかどうか、Blueqatで確認してみましょう。ch関数が制御アダマールゲートの演算に対応します。
from blueqat import Circuit
import numpy as np
# The number of qubits
N=2
# controlled Hadamard gate
def ch(circuit, control, target):
circuit.cx[control, target]
circuit.ry(-np.pi*0.25)[target]
circuit.cx[control, target]
circuit.ry(np.pi*0.25)[target]
circuit.cx[control, target]
return circuit
# Test
for k in range(2**N):
c=Circuit(N)
# bit
tmp = []
for shift in range(N-1, -1, -1):
tmp.append((k>>shift) & 0x01)
# X gate
for i, bit in enumerate(tmp):
if bit == 1:
c.x[i]
ret=ch(c, 0, 1).run(shots)
print("{}->{}".format(tmp, ret))
結果は以下のようになりました。制御ビットが1の場合のみ、標的ビットに対するアダマールゲートの演算が実現されていますね。
[0, 0]->[1.+0.j 0. +0.j 0.+0.j 0. +0.j]
[0, 1]->[0.+0.j 0. +0.j 1.+0.j 0. +0.j]
[1, 0]->[0.+0.j 0.70710678+0.j 0.+0.j 0.70710678+0.j]
[1, 1]->[0.+0.j 0.70710678+0.j 0.+0.j -0.70710678+0.j]
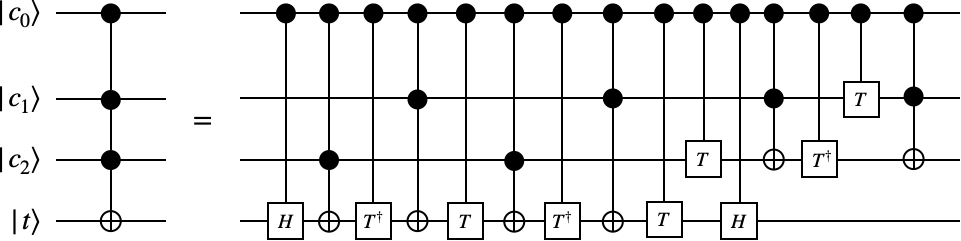
制御トフォリゲートの構成
以上で、トフォリゲートを構成するすべてのゲートに対して制御ゲートを準備することができました。制御アダマールゲート、制御位相ゲート、そしてトフォリゲート(制御CNOTゲート)により、以下の量子回路図で制御トフォリゲートを実現できます。
Blueqatで動作確認してみます。制御トフォリゲートはcccx関数で定義しました。
from blueqat import Circuit
import numpy as np
# The number of qubits
N=4
"""
Controlled phase gate
"""
def crz(circuit, phi, control, target):
circuit.rz(phi*0.5)[target]
circuit.cx[control, target]
circuit.rz(-phi*0.5)[target]
circuit.cx[control, target]
circuit.rz(phi*0.5)[control]
return circuit
"""
Controlled Hadamard gate
"""
def ch(circuit, control, target):
circuit.cx[control, target]
circuit.ry(-np.pi*0.25)[target]
circuit.cx[control, target]
circuit.ry(np.pi*0.25)[target]
circuit.cx[control, target]
return circuit
"""
Toffoli (Controlled controlled not: CCNOT) gate
"""
def ccx(circuit, control1, control2, target):
circuit.h[target]
circuit.cx[control2,target]
circuit.rz(-np.pi/4)[target]
circuit.cx[control1,target]
circuit.rz(np.pi/4)[target]
circuit.cx[control2,target]
circuit.rz(-np.pi/4)[target]
circuit.cx[control1,target]
circuit.rz(np.pi/4)[control2]
circuit.rz(np.pi/4)[target]
circuit.cx[control1,control2]
circuit.h[target]
circuit.rz(np.pi/4)[control1]
circuit.rz(-np.pi/4)[control2]
circuit.cx[control1,control2]
return circuit
"""
Controlled Toffoli gate
"""
def cccx(circuit, control, control1, control2, target):
# circuit.h[target]
ch(circuit, control, target)
ret=circuit.run()
# circuit.cx[control2,target]
ccx(circuit, control, control2, target)
# circuit.rz(-np.pi/4)[target]
crz(circuit, -np.pi*0.25, control, target)
# circuit.cx[control1,target]
ccx(circuit, control, control1, target)
# circuit.rz(np.pi/4)[target]
crz(circuit, np.pi*0.25, control, target)
# circuit.cx[control2,target]
ccx(circuit, control, control2, target)
# circuit.rz(-np.pi/4)[target]
crz(circuit, -np.pi*0.25, control, target)
# circuit.cx[control1,target]
ccx(circuit, control, control1, target)
# circuit.rz(np.pi/4)[control2]
crz(circuit, np.pi*0.25, control, control2)
# circuit.rz(np.pi/4)[target]
crz(circuit, np.pi*0.25, control, target)
# circuit.cx[control1,control2]
ccx(circuit, control, control1, control2)
# circuit.h[target]
ch(circuit, control, target)
# circuit.rz(np.pi/4)[control1]
crz(circuit, np.pi*0.25, control, control1)
# circuit.rz(-np.pi/4)[control2]
crz(circuit, -np.pi*0.25, control, control2)
# circuit.cx[control1,control2]
ccx(circuit, control, control1, control2)
return circuit
# test
for k in range(2**N):
c=Circuit(N)
# bit
tmp = []
for shift in range(N-1, -1, -1):
tmp.append((k>>shift) & 0x01)
# X gate
for index, bit in enumerate(tmp):
if bit == 1:
c.x[index]
ret=cccx(c, 0, 1, 2, 3).m[:].run(shots=100)
print("{}->{}".format(tmp, ret))
結果は以下のようになりました。3つの制御ビット(左から順に3個のビット)がすべて1のときのみ、標的ビット(右端のビット)が反転しています。正しく動作していますね。
[0, 0, 0, 0]->Counter({'0000': 100})
[0, 0, 0, 1]->Counter({'0001': 100})
[0, 0, 1, 0]->Counter({'0010': 100})
[0, 0, 1, 1]->Counter({'0011': 100})
[0, 1, 0, 0]->Counter({'0100': 100})
[0, 1, 0, 1]->Counter({'0101': 100})
[0, 1, 1, 0]->Counter({'0110': 100})
[0, 1, 1, 1]->Counter({'0111': 100})
[1, 0, 0, 0]->Counter({'1000': 100})
[1, 0, 0, 1]->Counter({'1001': 100})
[1, 0, 1, 0]->Counter({'1010': 100})
[1, 0, 1, 1]->Counter({'1011': 100})
[1, 1, 0, 0]->Counter({'1100': 100})
[1, 1, 0, 1]->Counter({'1101': 100})
[1, 1, 1, 0]->Counter({'1111': 100})
[1, 1, 1, 1]->Counter({'1110': 100})
おわりに
トフォリゲートを例に、制御ゲートの構成方法について解説しました。ユニバーサルゲートセットについて触れた際にも述べましたが、1量子ビットゲートとCNOTゲートを用意すれば、任意のユニタリ演算を近似することができます。この記事では、位相ゲート、アダマールゲートおよび制御NOTゲートの制御ゲート版について説明したので、ほとんどのユニタリ演算の制御ゲートが作れることになります。
シミュレータを動かして動作確認していますが、計算の怪しい箇所があるかもしれません。何かお気づきの方は、お手数ですがコメントをいただければと思います。