LoginSignup
10
6

More than 5 years have passed since last update.

Hot Soup ProcessorAdvent Calendar 2016Day 5
@exrd

HSPで8パズルを高速に解くまで

Last updated at Posted at 2016-12-05

ﾜﾀｼﾓ・・猫ｶﾜｲｲ・・ｼﾀｲ・・。
こんばんは、えく－です。

この記事は

HSPのAdventCalendar、略さず言うと Hot Soup Processor Advent Calendar 2016 の5日目の記事です。

この記事で書くこと

今年初め、HSP掲示板の”HSPでの、幅優先探索のプログラムの作り方”っていうスレッドがありました。
HSP掲示板で時々たまたま稀に出現するアルゴリ系の話題ですね、地味にレアリティが高いです。

私自身、そういえばHSPでこういうアルゴリ系の何かを実装したことってほとんどなかったので、改めてHSPってどういうことが出来たっけって思いながら手探りで色々試行錯誤してました。
結果、久方振りに触ってみて改めて分かった（思い出した、とも言う）ことなど出てきたので、折角の機会ですしまとめておこうと思いました。

ということで

この記事ではHSPで8パズルをを題材としてHSPでの（主に幅優先）探索について書いていきます。
また、実際に8パズルを解くコードの解説、更により高速に解くには、といった点についても触れていきます。

より具体的に触れる内容については下記。

  1. 盤面の表現、探索の基本
    • ある盤面から1手で得られる盤面の列挙
  2. HSPで幅優先探索
    • 列挙した盤面を配列に保存する
    • 既に列挙した盤面（重複盤面）のスキップする
  3. 一般的な高速化
    • 盤面表現の圧縮
      • ビットを詰める
    • 重複盤面チェックの高速化
      • 二分探索
    • 探索の改良
      • 双方向探索

2.までが初級者向けで、HSPで幅優先探索の概念を理解するだけならここまでで十分（予定）です。
それ以降は中級者向けのトピックで、こういった探索問題に一般的に適用可能な手法を導入してみます。

8パズル is 何

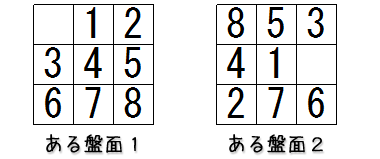
8パズルはスライドパズルの一種で、3 x 3の盤面に 1 から 8 までの数値が書かれた 8 つ駒が置かれており、駒が置かれていない一箇所の空白を使って数値が書かれた駒を特定の順に並び替える遊びです。
15パズルの簡易版で、もっと詳細な説明を求む方は普通にWikipedia先生（Wikipedia:15パズル）が詳しいのでそちらをどうぞ。

盤面をプログラムでどう表現しよう

盤面というのは、例えば次の画像のようなその時点での駒の並びのことを指します。

puzzle8_boardSample.png

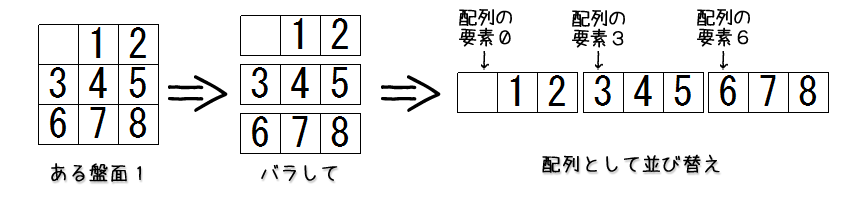
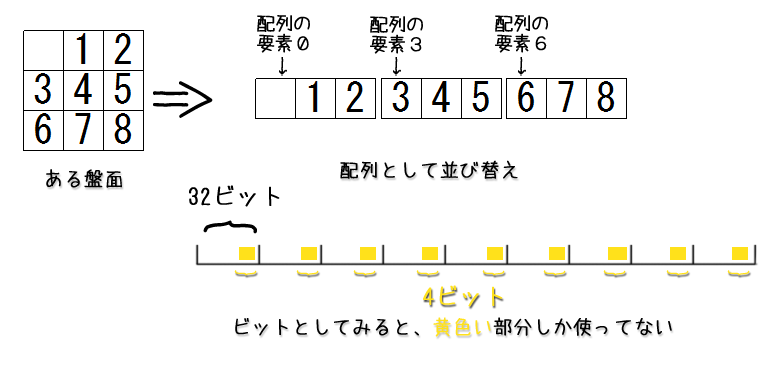
これをプログラムで参照、記録するためには、最も簡単には配列を使い、左上から右下に向かって順番に駒の値を記録していくことで実現できそうです。（というか実際できます）
駒とプログラム側での数値の対応関係は、空白の場合は0として、数値の駒の場合はその数値を入れておくことにしましょう。

puzzle8_boardArraySample.png

つまり、最初に示した盤面は、プログラム上は次のような配列になります。

ある盤面の配列による表現
// ある盤面１
board = 0, 1, 2, 3, 4, 5, 6, 7, 8

// ある盤面２
board = 8, 5, 3, 4, 1, 0, 2, 7, 6

盤面の描画

ついでなので、先に示した盤面をプログラムから描画できるコードも書いておきましょう。
プログラムのバグを見つけるのは何はともあれ可視化から。
printfデバッグも立派な可視化の一手段ですし、可視化して悪いことはデバッグ時のパフォーマンスぐらいなので、こういうのはさっさと書いておくと後々便利です。

puzzle8_boardProgramDraw.png

盤面の描画モジュール
#module
// 盤面の描画
// 起点X, 起点Y, 盤面配列, 描画サイズ
#deffunc drawBoard int cx, int cy, array board, int size
    bsz = size*3

    // 背景（下地）のクリア
    color 255, 255, 255 : boxf cx, cy, cx+bsz, cy+bsz

    // 枠線
    color 0, 0, 0
    repeat 4
        ofs = cnt*size
        line cx, cy+ofs, cx+bsz, cy+ofs
        line cx+ofs, cy, cx+ofs, cy+bsz
    loop
    // 駒
    font msgothic, size
    repeat 9
        cntXP3S = cx + cnt\3 * size
        cntXD3S = cy + cnt/3 * size
        color 0, 0, 0 : pos cntXP3S+size/4, cntXD3S
        if ( board(cnt) != 0 ) {// 空白じゃないなら
            mes ""+board(cnt)
        }
    loop
return
#global

// ある盤面１
board = 0, 1, 2, 3, 4, 5, 6, 7, 8
drawBoard 10, 10, board, 40

// ある盤面２
board = 8, 5, 3, 4, 1, 0, 2, 7, 6
drawBoard 150, 10, board, 40

探索の基本のキ

さてさて、それでは本題の8パズル解く話に入っていきます。

問題の整理

入力として最初の盤面と最後の盤面（目的の盤面）が与えられるので、最初の盤面からスライドパズルの要領で空白に駒を動かす操作をし、最後の盤面に辿り着く最小手数を求める問題とします。
求めるのは最後の盤面に辿り着くまでの最小手数だけで、最小手数の中身がどういう手なのかは一旦置いておきましょう、最初からそれをやるとかなり煩雑になるので。

コードで書くとこんな感じです。

最も基本的な処理の流れ
// 最初の盤面
start = 0, 1, 2, 3, 4, 5, 6, 7, 8
// 最後の盤面（目的の盤面）
goal = 0, 1, 2, 3, 4, 5, 6, 7, 8

// 最小手数を保存しておく変数
minStep = -1

// なにかして最小手数を求める

mes "最小手数は"+minStep+"です"

はい、見事に何もありません。
”なにかして最小手数を求める”ところをこれから考えていきましょう。

問題を解くための動作指針

と言っても、一回もこういった問題を解いたことがない場合、どう解けばいいかの指針すら分からないものです。
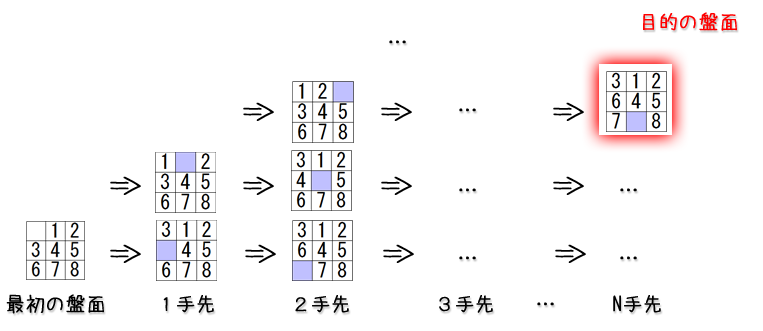
大体こういう問題はプログラムは単純な動作が高速なことを利用して、愚直には以下のような手順で解くのが基本です。

  1. 最初の盤面から1手で得られる盤面を列挙する
  2. 列挙した盤面の中に最後の盤面（目的の盤面）がないかチェックする、あったら終了、なかったら手順3.へ
  3. 列挙した盤面から更に1手で得られる盤面を列挙する
  4. 手順2.へ

つまり、およそ人の手では考えたくもない数の盤面を列挙し、列挙した盤面の一つ一つがそれぞれ目的の盤面であるかをチェックするわけです。
こう聞くとかなり力技であることが分かりますね。

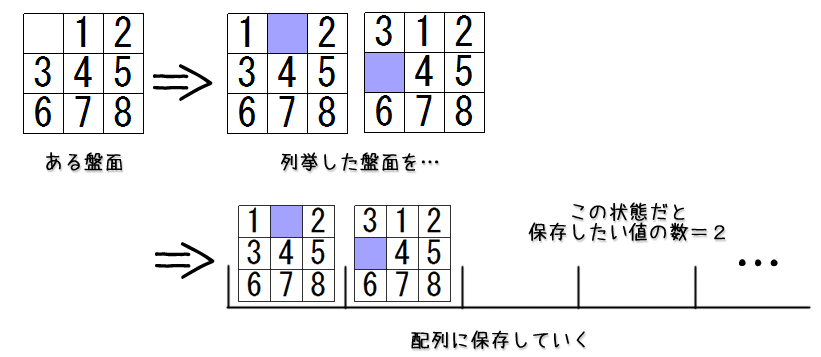
ある盤面から1手で得られる盤面を列挙する

さて、動作指針を示したところで、まずはその核となる動作の「ある盤面から1手で得られる盤面を列挙する」ところを考えてみましょう。

と言ってもまだ難しいところはなく、空白の位置を求めて、空白とその上下左右の駒を交換した盤面が1手で得られる盤面です。
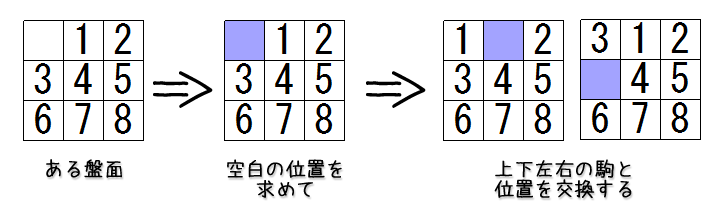
puzzle8_boardEnumeration_oneStep.png

上図では左上が空白だった場合を過程したので列挙できたのは2つの盤面だけですが、空白が真ん中にあった場合は最大で4つの盤面が列挙できることに注意してください。

手順は分かった、あとはプログラムを書くだけだ。

盤面の配列表現と実際の盤面上での位置関係

その前に一つ確認しておきます、上下左右の入れ替えは元の盤面上で行われます。
しかし、盤面の表現という意味でプログラム上では盤面は配列で表現されています。

ということで、ややこしいですが私達が頭の中で考えている盤面の駒の位置と、プログラム上の配列での位置は若干の変換が必要です。
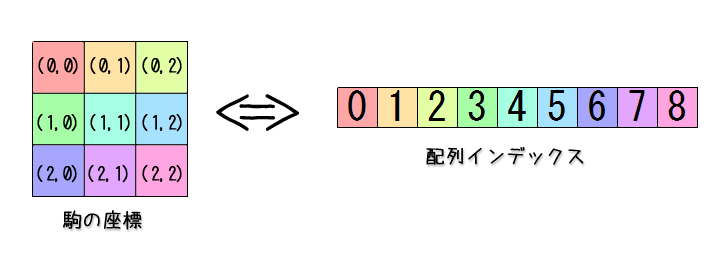
今回は実際の盤面は左上を$(0, 0)$、右下を$(2, 2)$とした二次元座標として考えます。
こう考えた時、盤面の座標$(x, y)$と配列インデックス$i$との間には次のような関係が成立します。

i = x + y*3

配列インデックス$i$から$(x, y)$を求める場合は、次のように求まります。

\begin{align}
x &= i \mod 3 \\
y &= i / 3
\end{align}

HGPだとmod（剰余）は「￥」演算子ですね。
なおこの変換、今後結構頻繁にでてきますので、ご注意ください。

puzzle8_boardArray2Grid.png

ある盤面から1手で得られる盤面を列挙する（再）

先述の駒の座標と、配列インデックスとの関係を踏まえた上で、次のような感じになります。

ある盤面から1手で得られる盤面をとりあえず列挙する
#module
// 盤面の中で空白のインデックスを返す
#defcfunc searchEmpty array board, local res
    res = -1
    repeat 9
        if ( board(cnt) == 0 ) {
            res = cnt
            break
        }
    loop
return res

// 盤面の中の2つの要素位置を交換する
#deffunc swapPiece array board, int piece1, int piece2, local t
    t = board(piece1)
    board(piece1) = board(piece2)
    board(piece2) = t
return
#global

//----------------------モジュールここまで

// ある盤面から…
board = 0, 1, 2, 3, 4, 5, 6, 7, 8
drawBoard 10, 10, board, 40

// 空白の配列インデックスを取得
emptyIdx = searchEmpty( board )

// 盤面中の空白のx位置、y位置　：左上を(0,0)、右下を(2.2)とする
emptyX = emptyIdx \3
emptyY = emptyIdx /3

// 上下左右の駒と交換できるなら交換した盤面を列挙する
repeat 4
    // 列挙する盤面
    dim newBoard, 9
    // とりあえず元のをコピー
    repeat 9 : newBoard(cnt) = board(cnt) : loop
    // 上下左右、どこに移動するか
    dx = 0 : dy = 0 : label=""
    switch( cnt )
        case 0 : dx =  0 : dy = -1 : label="上" : swbreak// 上
        case 1 : dx =  0 : dy =  1 : label="下" : swbreak// 下
        case 2 : dx =  1 : dy =  0 : label="右" : swbreak// 右
        case 3 : dx = -1 : dy =  0 : label="左" : swbreak// 左
    swend
    // 交換する駒のx位置、y位置
    swapX = emptyX + dx
    swapY = emptyY + dy
    // 交換する駒の位置が範囲外なら何もしない
    if ( swapX<0 || swapX>=3 || swapY<0 || swapY>=3 ) {
        continue
    }
    // 交換する駒の位置の配列インデックス
    swapIdx = swapX + swapY *3
    // 駒の交換
    swapPiece newBoard, emptyIdx, swapIdx
    // 描画
    drawBoard 10+140*cnt, 150, newBoard, 40
    pos 60+140*cnt, 280 : color 0, 0, 0 : mes ""+label
loop

プログラムも長くなってきましたね…。
今までと重複している箇所は削っていきますので、その辺はよろしくお願いします。

これを実行すると、board変数に入っていた盤面から1手で得られる盤面が列挙されます。
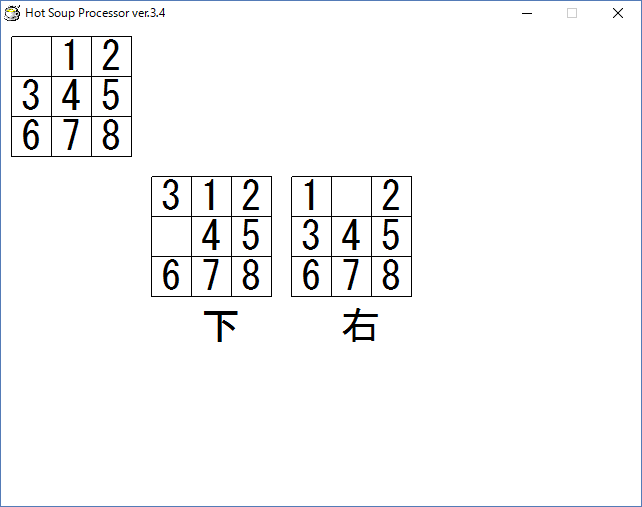
puzzle8_boardEnumeraton_oneStepSample.png

最初にboardに真ん中が空白の盤面を与えると、次のように4つの盤面が得られるのが確認できます。
puzzle8_boardEnumeraton_oneStepSample2.png

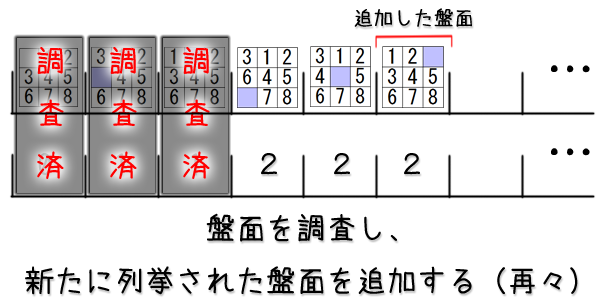
列挙した盤面から更に盤面を列挙する

盤面の列挙ができました、もうここで終わりたい気分ですが、大体HSPで8パズルを解く道のりの半分くらいにしか至ってないのでまだまだ続きます。1

さて本節では、列挙した盤面から更に1手で得られる盤面を列挙する動作についてです。
ある盤面から1手で得られる盤面の列挙については前節で述べましたし、そこまでは平ったくスクリプトを書き下すことで実現できます。
一方で、列挙した盤面から更に列挙を行うなど”いつまで続くか分からない”系の動作はちょっと工夫が必要になります。

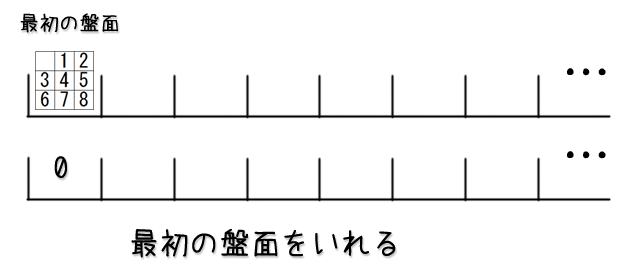
列挙した盤面を保存する・取り出す

いつまで列挙が続くか分からない系ですが、要は列挙したものを後でとってこれればまたそこから続けて1手で得られる盤面が列挙ができます。
ということで、列挙した盤面を保存しておくこと、そして保存しておいた盤面を後からとってこれる仕組みを考えていきましょう。

配列を使う

”沢山の盤面を保存する”ですが、盤面を一つの値として見てみたらどうでしょうか？
”沢山の値を保存する”という観点で見ると、HSPでは沢山の値を取り扱う仕組みとして配列がありますね。

HSPの配列は可変長ではないため可変長っぽい配列を扱いたい場合は、予め十分な数の要素が収められる配列を作っておき、いくつ保存されているかは別の変数で管理するのがよくやる奴です。

puzzle8_boardPushAndPopAsArray.png

とりあえず、前節までで説明した”ある盤面から1手で得られる盤面の列挙”した後、列挙した盤面を保存するコード。

列挙した盤面の保存
// 盤面保存のための配列
dim storedBoards, 100, 9// 適当に100個
storedBoardNum = 0// いくつ保存しているか

//---------------------ここから前回と同じ
// ある盤面から…

// ～～省略～～

    // 駒の交換
    swapPiece newBoard, emptyIdx, swapIdx
    //------------ここまでは前回と一緒

    // 列挙した盤面の保存
    repeat 9
        storedBoards(storedBoardNum, cnt) = newBoard(cnt)
    loop
    storedBoardNum++// 一個盤面保存したので足しとく
loop

//---------------------保存した盤面を取り出して描画
// 保存した盤面を後から描画
repeat storedBoardNum
    // 保存した盤面を取り出す
    peekBoardIdx = cnt
    dim board, 9
    repeat 9 : board(cnt) = storedBoards(peekBoardIdx, cnt) : loop
    // 描画
    drawBoard 10+140*peekBoardIdx, 150, board, 40
loop

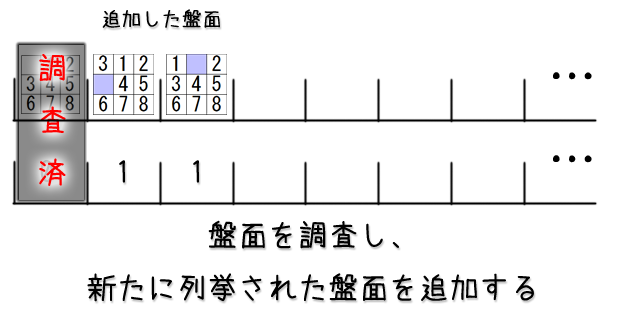
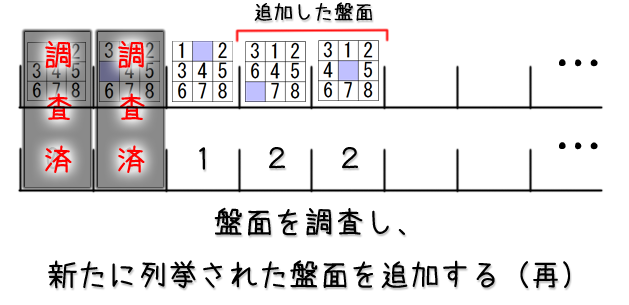
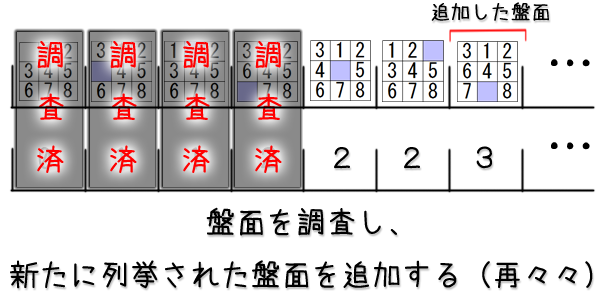
保存した盤面を取り出して更に列挙を続ける

さて、盤面を保存することができしたし、保存した盤面全部を描画するコードも前節で説明してしまいました。
結構ゴールが近づいてきていますが、盤面の保存と列挙を同時に行うにはもう少しだけ工夫が必要です。

実際に列挙を続けていくと、保存した盤面はどんどん増えていく訳ですが保存した盤面の中でどこまでは既に列挙を終えているかも覚えておかないと、同じ盤面が生成され続けていってしまいます。
ということで、盤面を保存する配列変数と、いくつ盤面を保存したか覚えておく変数の他に、保存した盤面の中で列挙を既に終えた数を覚えておく変数も別に必要になります。

これも踏まえてコードを書いてみましょう。

の前に

”最初の盤面から列挙した盤面”から更に列挙をしていくコードな訳ですが、よくよく考えるとこの”更に列挙していく”部分と、”最初の盤面から列挙する”部分はコード的に同じです。
そして、考え方を少し変えて”最初の盤面は誰かによって列挙された盤面”と捉えると、”最初の盤面”と”ある盤面から列挙された盤面”は等しく扱うことができる事に気付きます。

ここからは、最初の盤面は”誰かに列挙されたもの”として、盤面保存用の配列に追加しておくことにしましょう。
実際にコードを見てもらわないと分からないと思いますが、こうすることでそれなりにコードがシンプルになってきます。

盤面を次々に列挙していく
// 盤面保存のための配列
dim storedBoards, 100, 9// 適当に100個
storedBoardNum = 0// いくつ保存しているか
popedBoardNum = 0// 保存した盤面のうち、いくつ既に調べたか（更に列挙したか）

// 最初の盤面を、”誰かから列挙された”として追加
board = 0, 1, 2, 3, 4, 5, 6, 7, 8
drawBoard 10, 10, board, 40

repeat 9
    storedBoards(storedBoardNum, cnt) = board(cnt)
loop
storedBoardNum++

// 保存した盤面の中で、まだ更に列挙してないものがあったら更に列挙する
repeat
    // もう調べるものはないか？
    if ( popedBoardNum >= storedBoardNum ) : break

    // 調べる盤面として一個取り出す
    dim board, 9
    repeat 9 : board(cnt) = storedBoards(popedBoardnum, cnt) : loop
    popedBoardnum++

    // 空白の配列インデックスを取得
    emptyIdx = searchEmpty( board )

    // 盤面中の空白のx位置、y位置　：左上を(0,0)、右下を(2.2)とする
    emptyX = emptyIdx \3
    emptyY = emptyIdx /3

    // 上下左右の駒と交換できるなら交換した盤面を列挙する
    repeat 4
        // 列挙する盤面
        dim newBoard, 9
        // とりあえず元のをコピー
        repeat 9 : newBoard(cnt) = board(cnt) : loop
        // 上下左右、どこに移動するか
        dx = 0 : dy = 0 : label=""
        switch( cnt )
            case 0 : dx =  0 : dy = -1 : label="上" : swbreak// 上
            case 1 : dx =  0 : dy =  1 : label="下" : swbreak// 下
            case 2 : dx =  1 : dy =  0 : label="右" : swbreak// 右
            case 3 : dx = -1 : dy =  0 : label="左" : swbreak// 左
        swend
        // 交換する駒のx位置、y位置
        swapX = emptyX + dx
        swapY = emptyY + dy
        // 交換する駒の位置が範囲外なら何もしない
        if ( swapX<0 || swapX>=3 || swapY<0 || swapY>=3 ) {
            continue
        }
        // 交換する駒の位置の配列インデックス
        swapIdx = swapX + swapY *3
        // 駒の交換
        swapPiece newBoard, emptyIdx, swapIdx
        // 列挙した盤面の保存、もう保存できなかったら何もしない
        if ( storedBoardNum < length( storedBoards ) ) {
            repeat 9
                storedBoards(storedBoardNum, cnt) = newBoard(cnt)
            loop
            storedBoardNum++
        }
    loop
loop

// 保存した盤面を後から描画
repeat storedBoardNum
    // 保存した盤面を取り出す
    peekBoardIdx = cnt
    dim board, 9
    repeat 9 : board(cnt) = storedBoards(peekBoardIdx, cnt) : loop
    // 描画
    drawBoard 10+45*(peekBoardIdx\15), 150+45*(peekBoardIdx/15), board, 12
loop

一応、一回ここでモジュール部分の除いたコードは全て省略せず載せておきました。
盤面保存用の配列はとりあえず100個分しか保存できないので、エラー落ちとかしないように保存できなそうだったら保存スキップしてます。
ここまでで、最初の盤面から1手で得られる盤面を連続して列挙できるようになりました。
puzzle8_boardEnumeration_max100.png

目的の盤面判定と、かかった手数の計算

次々列挙が出来るようになったので、あとは目的の盤面になったかの判定を追加すればよさそうです。
それ自体は簡単で、ループ内で列挙のため一つの盤面を取り出していますが、その取り出した盤面が目的の盤面だったら探索を終えれば良い、というコードを書くだけです。

目的の盤面かチェック
// ～～省略～～
// 最初の盤面を、”誰かから列挙された”として追加
board = 0, 1, 2, 3, 4, 5, 6, 7, 8
drawBoard 10, 10, board, 40

repeat 9
    storedBoards(storedBoardNum, cnt) = board(cnt)
loop
storedBoardNum++

// 目的の盤面
objectiveBoard = 3, 1, 2, 4, 7, 5, 6, 0, 8
drawBoard 180, 10, objectiveBoard, 40

// 保存した盤面の中で、まだ更に列挙してないものがあったら更に列挙する
repeat
    // もう調べるものはないか？
    if ( popedBoardNum >= storedBoardNum ) : break

    // 調べる盤面として一個取り出す
    dim board, 9
    repeat 9 : board(cnt) = storedBoards(popedBoardnum, cnt) : loop
    popedBoardnum++

    // 目的の盤面かチェック
    isObjectiveBoard = 1
    repeat 9
        if ( board(cnt) != objectiveBoard(cnt) ) {
            isObjectiveBoard = 0
            break
        }
    loop
    if ( isObjectiveBoard ) {
        dialog "見つかった！！"
        break
    }

    // ～～省略～～

そして、何手かかったかを覚えておくには、ですがこちらは保存しておく盤面と同じ長さの配列をもう一個用意しておいて、そっちに最初の盤面から何手目で辿り着いた盤面かを記録しておけば大丈夫そうです。
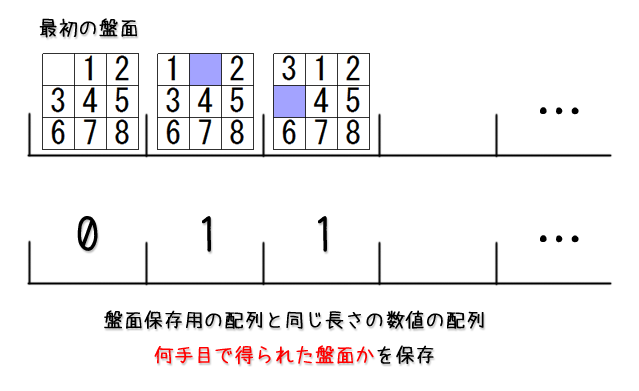
puzzle8_boardEnumeration_searchObjectiveStep.png

また、列挙の際は、新しく列挙する盤面は元の盤面から1手で得られるものなので、元の盤面＋１手で得られる盤面とすればよさそうです。

以上を整理して、コードを少し弄ります。

何手目で盤面が得られるかも保存しながら列挙
// ～～省略～～
// 最初の盤面を、”誰かから列挙された”として追加
board = 0, 1, 2, 3, 4, 5, 6, 7, 8
drawBoard 10, 10, board, 40

repeat 9
    storedBoards(storedBoardNum, cnt) = board(cnt)
loop
storedBoardSteps(storedBoardNum) = 0// 最初の盤面は、0手で辿り着いた、とする
storedBoardNum++

// ～～省略～～
    // 調べる盤面として一個取り出す
    dim board, 9
    repeat 9 : board(cnt) = storedBoards(popedBoardnum, cnt) : loop
    boardRequiredStepNum = storedBoardSteps(popedBoardnum)// 何手目でこの盤面は得られるか
    popedBoardnum++

// ～～省略～～
        // 列挙した盤面の保存、もう保存できなかったら何もしない
        if ( storedBoardNum < length( storedBoards ) ) {
            repeat 9
                storedBoards(storedBoardNum, cnt) = newBoard(cnt)
            loop
            storedBoardSteps(storedBoardNum) = boardRequiredStepNum+1// 自分の盤面＋１
            storedBoardNum++
        }

これで探索を行わせると、無事何手でたどり着くかも分かるようになりました。
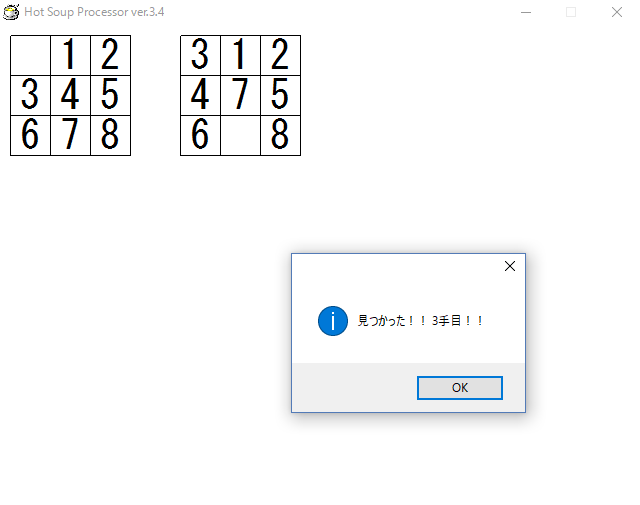
puzzle8_boardEnumeration_searchObjectiveAndGoal.png

ちなみに上記画像の目的の盤面（右側）は、最初の盤面（左側）から

  1. 空白と３を交換
  2. 空白と４を交換
  3. 空白と７を交換

とすると得られます、つまり合ってる！
勝ったッ！　第3部完！

盤面の重複をなくす

さて、列挙までできたし、ゴールに辿り着いた判定までできたので、一応の完成が…と思うでしょうが、よくよく列挙内容を見てください。
実は同じ盤面列挙しちゃってたりしますよね？

過去に列挙したものは盤面保存配列に全て保存されているので、既に列挙したものは追加で保存しないようにしましょう。

考えられる盤面数の最大

重複をなくした後、後は今まで適当に決めていた盤面保存用の配列サイズについてもちゃんと考えておきましょう。
8パズルで考えられる盤面の数は、左上から9種類の駒（正確には8個の駒と空白）を並べる操作になるので$9!$となりそうですが、盤面は空白をスライドして得られるという制約から実はこの半分の$9!/2$で得られることが知られています。
つまり$9!/2 = 181440$個ですね、最大数はこれにしておきましょう。

これで本当に完成ですので、モジュール含めコードを全部書きます。

ナイーブに8パズルを解く
#module
// 盤面の描画
// 起点X, 起点Y, 盤面配列, 描画サイズ
#deffunc drawBoard int cx, int cy, array board, int size
    bsz = size*3

    // 背景（下地）のクリア
    color 255, 255, 255 : boxf cx, cy, cx+bsz, cy+bsz

    // 枠線
    color 0, 0, 0
    repeat 4
        ofs = cnt*size
        line cx, cy+ofs, cx+bsz, cy+ofs
        line cx+ofs, cy, cx+ofs, cy+bsz
    loop
    // 駒
    font msgothic, size
    repeat 9
        cntXP3S = cx + cnt\3 * size
        cntXD3S = cy + cnt/3 * size
        color 0, 0, 0 : pos cntXP3S+size/4, cntXD3S
        if ( board(cnt) != 0 ) {// 空白じゃないなら
            mes ""+board(cnt)
        }
    loop
return

// 盤面の中で空白のインデックスを返す
#defcfunc searchEmpty array board, local res
    res = -1
    repeat 9
        if ( board(cnt) == 0 ) {
            res = cnt
            break
        }
    loop
return res

// 盤面の中の2つの要素位置を交換する
#deffunc swapPiece array board, int piece1, int piece2, local t
    t = board(piece1)
    board(piece1) = board(piece2)
    board(piece2) = t
return
#global

// 盤面保存のための配列
dim storedBoards, 181440, 9// 9!/2
dim storedBoardSteps, 181440// 何手目で辿り着いたか
storedBoardNum = 0// いくつ保存しているか
popedBoardNum = 0// 保存した盤面のうち、いくつ既に調べたか（更に列挙したか）

// 最初の盤面を、”誰かから列挙された”として追加
board = 0, 1, 2, 3, 4, 5, 6, 7, 8
drawBoard 10, 10, board, 40

repeat 9
    storedBoards(storedBoardNum, cnt) = board(cnt)
loop
storedBoardSteps(storedBoardNum) = 0// 最初の盤面は、0手で辿り着いた、とする
storedBoardNum++

// 目的の盤面
objectiveBoard = 3, 1, 2, 4, 7, 5, 6, 0, 8
drawBoard 180, 10, objectiveBoard, 40

// 保存した盤面の中で、まだ更に列挙してないものがあったら更に列挙する
repeat
    // もう調べるものはないか？
    if ( popedBoardNum >= storedBoardNum ) : break

    // 調べる盤面として一個取り出す
    dim board, 9
    repeat 9 : board(cnt) = storedBoards(popedBoardnum, cnt) : loop
    boardRequiredStepNum = storedBoardSteps(popedBoardnum)// 何手目でこの盤面は得られるか
    popedBoardnum++

    // 目的の盤面かチェック
    isObjectiveBoard = 1
    repeat 9
        if ( board(cnt) != objectiveBoard(cnt) ) {
            isObjectiveBoard = 0
            break
        }
    loop
    if ( isObjectiveBoard ) {
        dialog "見つかった！！ "+boardRequiredStepNum+"手目！！"
        break
    }

    // 空白の配列インデックスを取得
    emptyIdx = searchEmpty( board )

    // 盤面中の空白のx位置、y位置　：左上を(0,0)、右下を(2.2)とする
    emptyX = emptyIdx \3
    emptyY = emptyIdx /3

    // 上下左右の駒と交換できるなら交換した盤面を列挙する
    repeat 4
        // 列挙する盤面
        dim newBoard, 9
        // とりあえず元のをコピー
        repeat 9 : newBoard(cnt) = board(cnt) : loop
        // 上下左右、どこに移動するか
        dx = 0 : dy = 0 : label=""
        switch( cnt )
            case 0 : dx =  0 : dy = -1 : label="上" : swbreak// 上
            case 1 : dx =  0 : dy =  1 : label="下" : swbreak// 下
            case 2 : dx =  1 : dy =  0 : label="右" : swbreak// 右
            case 3 : dx = -1 : dy =  0 : label="左" : swbreak// 左
        swend
        // 交換する駒のx位置、y位置
        swapX = emptyX + dx
        swapY = emptyY + dy
        // 交換する駒の位置が範囲外なら何もしない
        if ( swapX<0 || swapX>=3 || swapY<0 || swapY>=3 ) {
            continue
        }
        // 交換する駒の位置の配列インデックス
        swapIdx = swapX + swapY *3
        // 駒の交換
        swapPiece newBoard, emptyIdx, swapIdx

        // 既に保存した盤面か調べる
        isAlreadySearched = 0
        repeat storedBoardNum
            peekBoardIdx = cnt
            isSame = 1
            repeat 9
                if ( storedBoards(peekBoardIdx, cnt) != newBoard(cnt) ) {
                    isSame = 0
                    break
                }
            loop
            if ( isSame ) {
                isAlreadySearched = 1
                break
            }
        loop

        // 既に保存した盤面だったら何もしないで次へ
        if ( isAlreadySearched ) : continue

        // 列挙した盤面の保存、もう保存できなかったら何もしない
        if ( storedBoardNum < length( storedBoards ) ) {
            repeat 9
                storedBoards(storedBoardNum, cnt) = newBoard(cnt)
            loop
            storedBoardSteps(storedBoardNum) = boardRequiredStepNum+1// 自分の盤面＋１
            storedBoardNum++
        }
    loop
loop

いやー、ホントに長い戦いだった、お疲れ様です。2

最短であることの証明と、幅優先探索と

ここまででざっくり説明してきた訳ですが、説明してきたことと言えば

  1. ある盤面から1手で得られる盤面を列挙する
  2. 盤面の保存と、列挙を組み合わせた処理
  3. 列挙の時に何手で得られたかを保存しておく

だけで、実は得られた解が本当に最小手数なのかの保証ってしてなかったんですよね、ウッカリ。
それに、冒頭で説明した幅優先探索についても触れてないし、この筆者の頭沸いてるのでは…と思った方、素晴らしい、慧眼ですね。
ということで、ここからは今までのコードで大丈夫なことを処理を可視化することによって説明するのと、幅優先探索との絡みを説明したいと思います。

処理フローを考え直してみる

書いたコードの動作を少しだけ追っていきましょう。

  1. まず、最初の盤面を盤面保存配列に入れます
    puzzle8_searchVis_step0.png

  2. まだ調べていない、盤面保存用配列に入っている盤面を調べ、新しく列挙されたものを追加する
    puzzle8_searchVis_step1.png

  3. 2.をもう一回
    puzzle8_searchVis_step2.png

  4. 2.をもう一回
    puzzle8_searchVis_step3.png

  5. 2.をもう一回
    puzzle8_searchVis_step4.png

…もうそろそろ見えてきたかもしれません。

下段の「最初の盤面から何手で辿り着くか」を表す数値に注目していただきたいのですが、この処理をしていると最初の盤面から少ない手数で辿り着く盤面が先に列挙されることが分かります。
つまり、この手順で目的の盤面が見つかった場合、その時保存していた手数が最小であることが保証されるわけです。

…という、全く証明にも何もなってなかったりするんですが、そんな感じ。

幅優先探索

幅優先探索との絡みですが、元々幅優先探索とはグラフやツリー上のノードをどのように調べていくのか（探索するのか）、その処理順を表す用語です、
そして、幅優先探索は探索順としては、グラフやツリー上で距離が近いものから順に探索されるという性質を持ちます。
そう、上記で述べたものと同じですね。

実はこれまで述べた盤面の列挙の仕方は、ちょうど盤面をグラフ上の1ノード、ノード間の距離を遷移に必要な最小手数として定義した時の幅優先探索と一致します。

って言われてもワカランよ、図で示してよ

ここは余裕があったら後で書く、スマンナ。（しんだ魚の目）

結び

ここまでで8パズルを解くことが出来るようになりました、ﾔｯﾀｰ！

めでたしめでたし…

高速化の一手

…とすべきかは個人によると思いますが、実行してみると分かる通り解を求めるのがとても遅いです。
とても実用（？）に耐えるものではありません。
最小手数が30を超えるものはサクッと何秒後に、みたいな気軽さで求まりません。

ここからはどうすれば探索を高速化できるのか、一般的な手法についての導入と簡単な解説をつけて説明していきます。
冒頭でも説明しましたが、ここからはHSP中級者以上が対象で、内容についても少しばかり重いものになっています。

現状確認

とりあえず、現状でどの手数でどれくらい時間を使うのか、調べておきましょう。
テストケースつきで、かつ時間計測もついているコードが次。

手数数と時間計測
#include "winmm.as"

#module
// 盤面の描画
// 起点X, 起点Y, 盤面配列, 描画サイズ
#deffunc drawBoard int cx, int cy, array board, int size
    bsz = size*3

    // 背景（下地）のクリア
    color 255, 255, 255 : boxf cx, cy, cx+bsz, cy+bsz

    // 枠線
    color 0, 0, 0
    repeat 4
        ofs = cnt*size
        line cx, cy+ofs, cx+bsz, cy+ofs
        line cx+ofs, cy, cx+ofs, cy+bsz
    loop
    // 駒
    font msgothic, size
    repeat 9
        cntXP3S = cx + cnt\3 * size
        cntXD3S = cy + cnt/3 * size
        color 0, 0, 0 : pos cntXP3S+size/4, cntXD3S
        if ( board(cnt) != 0 ) {// 空白じゃないなら
            mes ""+board(cnt)
        }
    loop
return

// 盤面の中で空白のインデックスを返す
#defcfunc searchEmpty array board, local res
    res = -1
    repeat 9
        if ( board(cnt) == 0 ) {
            res = cnt
            break
        }
    loop
return res

// 盤面の中の2つの要素位置を交換する
#deffunc swapPiece array board, int piece1, int piece2, local t
    t = board(piece1)
    board(piece1) = board(piece2)
    board(piece2) = t
return
#global

// 盤面保存のための配列
dim storedBoards, 181440, 9// 9!/2
dim storedBoardSteps, 181440// 何手目で辿り着いたか
storedBoardNum = 0// いくつ保存しているか
popedBoardNum = 0// 保存した盤面のうち、いくつ既に調べたか（更に列挙したか）

// 最初の盤面を、”誰かから列挙された”として追加
board = 0, 1, 2, 3, 4, 5, 6, 7, 8
drawBoard 10, 10, board, 40

repeat 9
    storedBoards(storedBoardNum, cnt) = board(cnt)
loop
storedBoardSteps(storedBoardNum) = 0// 最初の盤面は、0手で辿り着いた、とする
storedBoardNum++

// 目的の盤面
objectiveBoard = 3, 1, 2, 4, 7, 5, 6, 0, 8// 3手
//objectiveBoard = 3, 1, 2, 4, 7, 0, 6, 8, 5// 5手
//objectiveBoard = 0, 1, 5, 3, 2, 8, 6, 4, 7// 8手
//objectiveBoard = 3, 1, 5, 2, 4, 8, 6, 0, 7// 11手
//objectiveBoard = 3, 1, 0, 2, 7, 5, 6, 8, 4// 12手
//objectiveBoard = 3, 0, 1, 2, 7, 5, 6, 8, 4// 13手
//objectiveBoard = 0, 1, 2, 4, 7, 5, 6, 3, 8// 14手
//objectiveBoard = 7, 6, 2, 1, 5, 0, 3, 4, 8// 15手
//objectiveBoard = 4, 2, 8, 1, 0, 5, 6, 7, 3// 16手
//objectiveBoard = 4, 0, 5, 1, 8, 2, 6, 7, 3// 17手
drawBoard 180, 10, objectiveBoard, 40

// 開始時間
timeGetTime : st = stat

// 保存した盤面の中で、まだ更に列挙してないものがあったら更に列挙する
repeat
    // もう調べるものはないか？
    if ( popedBoardNum >= storedBoardNum ) : break

    // 調べる盤面として一個取り出す
    dim board, 9
    repeat 9 : board(cnt) = storedBoards(popedBoardnum, cnt) : loop
    boardRequiredStepNum = storedBoardSteps(popedBoardnum)// 何手目でこの盤面は得られるか
    popedBoardnum++

    // 目的の盤面かチェック
    isObjectiveBoard = 1
    repeat 9
        if ( board(cnt) != objectiveBoard(cnt) ) {
            isObjectiveBoard = 0
            break
        }
    loop
    if ( isObjectiveBoard ) {
        break
    }

    // 空白の配列インデックスを取得
    emptyIdx = searchEmpty( board )

    // 盤面中の空白のx位置、y位置　：左上を(0,0)、右下を(2.2)とする
    emptyX = emptyIdx \3
    emptyY = emptyIdx /3

    // 上下左右の駒と交換できるなら交換した盤面を列挙する
    repeat 4
        // 列挙する盤面
        dim newBoard, 9
        // とりあえず元のをコピー
        repeat 9 : newBoard(cnt) = board(cnt) : loop
        // 上下左右、どこに移動するか
        dx = 0 : dy = 0 : label=""
        switch( cnt )
            case 0 : dx =  0 : dy = -1 : label="上" : swbreak// 上
            case 1 : dx =  0 : dy =  1 : label="下" : swbreak// 下
            case 2 : dx =  1 : dy =  0 : label="右" : swbreak// 右
            case 3 : dx = -1 : dy =  0 : label="左" : swbreak// 左
        swend
        // 交換する駒のx位置、y位置
        swapX = emptyX + dx
        swapY = emptyY + dy
        // 交換する駒の位置が範囲外なら何もしない
        if ( swapX<0 || swapX>=3 || swapY<0 || swapY>=3 ) {
            continue
        }
        // 交換する駒の位置の配列インデックス
        swapIdx = swapX + swapY *3
        // 駒の交換
        swapPiece newBoard, emptyIdx, swapIdx

        // 既に保存した盤面か調べる
        isAlreadySearched = 0
        repeat storedBoardNum
            peekBoardIdx = cnt
            isSame = 1
            repeat 9
                if ( storedBoards(peekBoardIdx, cnt) != newBoard(cnt) ) {
                    isSame = 0
                    break
                }
            loop
            if ( isSame ) {
                isAlreadySearched = 1
                break
            }
        loop

        // 既に保存した盤面だったら何もしないで次へ
        if ( isAlreadySearched ) : continue

        // 列挙した盤面の保存、もう保存できなかったら何もしない
        if ( storedBoardNum < length( storedBoards ) ) {
            repeat 9
                storedBoards(storedBoardNum, cnt) = newBoard(cnt)
            loop
            storedBoardSteps(storedBoardNum) = boardRequiredStepNum+1// 自分の盤面＋１
            storedBoardNum++
        }
    loop

    // 適当にwaitをいれる
    if ( (popedBoardnum\500) == 0 ) {
        title "調べた盤面数　：　"+popedBoardnum
        await 0
    }
loop

// かかった時間
timeGetTime : ed = stat
delta = ed -st

color 0, 0, 0 : pos 10, 200 : font msgothic, 20
mes "手数　：　"+boardRequiredStepNum
mes "かかった時間　＝　"+(delta)+"ミリ秒"
mes "列挙した盤面数　＝　"+(storedBoardNum)
mes "調べた盤面数　＝　"+(popedBoardnum)

目的盤面（objectiveBoard）にコメントアウトで、必要な最小手数と一緒にテストケースを追加しておきました。
現状のコードでの必要時間をテーブル化しておくと次のような感じ。

手数 時間（ミリ秒） 列挙した盤面数 調べた盤面数
3 0 19 10
5 2 63 38
8 40 394 252
11 671 1737 1043
12 1744 2791 1791
13 4584 4613 2792
14 7209 5706 3575
15 18602 8934 5678
16 58894 15887 10544
17 144159 25207 16317

筆者の環境での計測結果です、計測環境によって結果が変わるのはご容赦ください。
18手目以上はスゴイ時間かかるので、やめました。
8パズルは最長手数が31手なので、そこまでやろうとすると何日か、何週間か、あるいはもっとかかりそうですね。

盤面表現の圧縮

これまでは盤面の表現に配列を用いてきました。
それぞれの駒を表すのに配列の要素 1 つを消費していた形ですね。

もし盤面を表すのにより少ない要素数の配列で表すことが出来たら、盤面の重複をチェックする過程で要素の比較をするループが減るので、高速化できると考えられます。
ということで、この盤面の表現をどうにか圧縮することを考えます。

ところで、駒の種類は空白も含めて僅か 9 種類しかありません。
1 つの駒を表すのに本質的に必要なのは僅か 4 ビットです。（2 の 3 乗は 8 で、ギリギリ 3 ビットに収まらない）
つまりある盤面を表現するのに必要なのは 4 x9 で 36 ビットです。（なお、補足しておくと話を簡単にするためにこう書いてますが、本質的に必要なビット数はもっと少ないです）

HSPで配列は 1 要素につき 32 ビットなので、盤面を表すのに32 x 9 で 282 ビットも使っていたことになります。
こうやって数値で計算すると結構大食いしてたことが分かりますね。

puzzle8_boardExpression_shrink.png

それでは要らないビットを捨て、32 ビットに 4 ビットずつ駒を格納していくと、配列としてはなんと 2 要素に収めることができます。
今までは特定の盤面を表すのに 9 要素使っていたので、9 ⇒ 2 と圧縮できました、スゴイ！！

で満足するのはまだ早くて…

9 ⇒ 2 の圧縮でも凄いことではあるのですが、やっぱりちょっと悔しいですよね、2要素目は 1要素目に収まりきらなかった 4 ビットしかないので、やっぱり無駄にしているところがまだあります。

ところで、よくよく考えると駒は 9 種類で決まっているので、8 つの駒の位置と種類が分かれば、残り 1 つは計算で求めることが可能ですよね。
この点に気づくと最後の 4 ビットは実は盤面の表現・保存という意味では必要ないことが分かります。

今回は単純に盤面をビットで圧縮＋1駒削減して 32 ビットの盤面表現を得ましたが、これは見方によっては盤面の（完全）ハッシュ化ともとれます。

コード上では

データ構造が変わるので、盤面を使った計算の随所をガラリと変える必要があります。
今まではarrayで受け取っていた盤面がintになります。
盤面の比較はint型の比較一回で済みます。

色々コードが改変されていますが、全コードは次。
先述の時間計測機能つきのものをベースにしました。

盤面表現を圧縮して8パズルを解く
#include "winmm.as"

#module
// 盤面の描画
// 起点X, 起点Y, 盤面配列, 描画サイズ
#deffunc drawBoard int cx, int cy, int board, int size
    bsz = size*3

    // 背景（下地）のクリア
    color 255, 255, 255 : boxf cx, cy, cx+bsz, cy+bsz

    // 枠線
    color 0, 0, 0
    repeat 4
        ofs = cnt*size
        line cx, cy+ofs, cx+bsz, cy+ofs
        line cx+ofs, cy, cx+ofs, cy+bsz
    loop
    // 駒
    font msgothic, size
    repeat 9
        cntXP3S = cx + cnt\3 * size
        cntXD3S = cy + cnt/3 * size
        color 0, 0, 0 : pos cntXP3S+size/4, cntXD3S
        if ( nth(board, cnt) != 0 ) {// 空白じゃないなら
            mes ""+nth(board, cnt)
        }
    loop
return

// 盤面のインデックスからその駒を返す
#defcfunc nth int board, int idx
    if ( idx >= 8 ) {
        sum = 0
        repeat 8
            sum += nth(board, cnt)
        loop
        return 36 - sum
    }
return ( board >> (idx*4) ) & 0x0f

// 駒とインデックスから盤面のint表現での値を返す
#defcfunc toNth int value, int idx
    if ( idx >= 8 ) : return 0
return ( value & 0x0f ) << (idx*4)

// 9つの駒を受け取って盤面を返す
#defcfunc makeBoard int p1, int p2, int p3, int p4, int p5, int p6, int p7, int p8, int p9
return toNth(p1,0)+toNth(p2,1)+toNth(p3,2)+toNth(p4,3)+toNth(p5,4)+toNth(p6,5)+toNth(p7,6)+toNth(p8,7)// p9は使わない

// 盤面の中で空白のインデックスを返す
#defcfunc searchEmpty int board, local res
    res = -1
    repeat 9
        if ( nth(board, cnt) ) : continue
        res = cnt
        break
    loop
return res

// 盤面の中の2つの要素位置を交換し、その盤面を返す
#defcfunc swapPiece int board, int piece1, int piece2, local t
    n1 = nth(board, piece1) : n2 = nth(board, piece2)
return board - toNth(n1, piece1) - toNth(n2, piece2) + toNth(n1, piece2) + toNth(n2, piece1)
#global

// 盤面保存のための配列
dim storedBoards, 181440// 9!/2
dim storedBoardSteps, 181440// 何手目で辿り着いたか
storedBoardNum = 0// いくつ保存しているか
popedBoardNum = 0// 保存した盤面のうち、いくつ既に調べたか（更に列挙したか）

// 最初の盤面を、”誰かから列挙された”として追加
board = makeBoard( 0, 1, 2, 3, 4, 5, 6, 7, 8 )
drawBoard 10, 10, board, 40

storedBoards(storedBoardNum) = board
storedBoardSteps(storedBoardNum) = 0// 最初の盤面は、0手で辿り着いた、とする
storedBoardNum++

// 目的の盤面
objectiveBoard = makeBoard( 3, 1, 2, 4, 7, 5, 6, 0, 8 )// 3手
//objectiveBoard = makeBoard( 3, 1, 2, 4, 7, 0, 6, 8, 5 )// 5手
//objectiveBoard = makeBoard( 0, 1, 5, 3, 2, 8, 6, 4, 7 )// 8手
//objectiveBoard = makeBoard( 3, 1, 5, 2, 4, 8, 6, 0, 7 )// 11手
//objectiveBoard = makeBoard( 3, 1, 0, 2, 7, 5, 6, 8, 4 )// 12手
//objectiveBoard = makeBoard( 3, 0, 1, 2, 7, 5, 6, 8, 4 )// 13手
//objectiveBoard = makeBoard( 0, 1, 2, 4, 7, 5, 6, 3, 8 )// 14手
//objectiveBoard = makeBoard( 7, 6, 2, 1, 5, 0, 3, 4, 8 )// 15手
//objectiveBoard = makeBoard( 4, 2, 8, 1, 0, 5, 6, 7, 3 )// 16手
//objectiveBoard = makeBoard( 4, 0, 5, 1, 8, 2, 6, 7, 3 )// 17手
drawBoard 180, 10, objectiveBoard, 40

// 開始時間
timeGetTime : st = stat

// 保存した盤面の中で、まだ更に列挙してないものがあったら更に列挙する
repeat
    // もう調べるものはないか？
    if ( popedBoardNum >= storedBoardNum ) : break

    // 調べる盤面として一個取り出す
    board = storedBoards(popedBoardnum)
    boardRequiredStepNum = storedBoardSteps(popedBoardnum)// 何手目でこの盤面は得られるか
    popedBoardnum++

    // 目的の盤面かチェック
    isObjectiveBoard = ( board == objectiveBoard )
    if ( isObjectiveBoard ) {
        break
    }

    // 空白の配列インデックスを取得
    emptyIdx = searchEmpty( board )

    // 盤面中の空白のx位置、y位置　：左上を(0,0)、右下を(2.2)とする
    emptyX = emptyIdx \3
    emptyY = emptyIdx /3

    // 上下左右の駒と交換できるなら交換した盤面を列挙する
    repeat 4
        // 列挙する盤面
        // とりあえず元のをコピー
        newBoard = board
        // 上下左右、どこに移動するか
        dx = 0 : dy = 0 : label=""
        switch( cnt )
            case 0 : dx =  0 : dy = -1 : label="上" : swbreak// 上
            case 1 : dx =  0 : dy =  1 : label="下" : swbreak// 下
            case 2 : dx =  1 : dy =  0 : label="右" : swbreak// 右
            case 3 : dx = -1 : dy =  0 : label="左" : swbreak// 左
        swend
        // 交換する駒のx位置、y位置
        swapX = emptyX + dx
        swapY = emptyY + dy
        // 交換する駒の位置が範囲外なら何もしない
        if ( swapX<0 || swapX>=3 || swapY<0 || swapY>=3 ) {
            continue
        }
        // 交換する駒の位置の配列インデックス
        swapIdx = swapX + swapY *3
        // 駒の交換
        newBoard = swapPiece( newBoard, emptyIdx, swapIdx )

        // 既に保存した盤面か調べる
        isAlreadySearched = 0
        repeat storedBoardNum
            peekBoardIdx = cnt
            isSame = ( storedBoards(peekBoardIdx) == newBoard )
            if ( isSame ) {
                isAlreadySearched = 1
                break
            }
        loop

        // 既に保存した盤面だったら何もしないで次へ
        if ( isAlreadySearched ) : continue

        // 列挙した盤面の保存、もう保存できなかったら何もしない
        if ( storedBoardNum < length( storedBoards ) ) {
            storedBoards(storedBoardNum) = newBoard
            storedBoardSteps(storedBoardNum) = boardRequiredStepNum+1// 自分の盤面＋１
            storedBoardNum++
        }
    loop

    // 適当にwaitをいれる
    if ( (popedBoardnum\500) == 0 ) {
        title "調べた盤面数　：　"+popedBoardnum
        await 0
    }
loop

// かかった時間
timeGetTime : ed = stat
delta = ed -st

color 0, 0, 0 : pos 10, 200 : font msgothic, 20
mes "手数　：　"+boardRequiredStepNum
mes "かかった時間　＝　"+(delta)+"ミリ秒"
mes "列挙した盤面数　＝　"+(storedBoardNum)
mes "調べた盤面数　＝　"+(popedBoardnum)

時間計測結果は次。

手数 時間（ミリ秒） 参考：元の時間（ミリ秒） 列挙した盤面数 調べた盤面数
3 0 0 19 10
5 1 2 63 38
8 21 40 394 252
11 329 671 1737 1043
12 849 1744 2791 1791
13 2278 4584 4613 2792
14 3571 7209 5706 3575
15 8744 18602 8934 5678
16 29104 58894 15887 10544
17 72138 144159 25207 16317

大体2倍くらい早くなった感じでしょうか、やっといてなんですが微妙ですね；；
圧縮したので比較と保存は早くなったけど、駒の交換などで計算が増えた箇所もあったのでそこまで劇的な高速化には至らなかったようです。
ただ、盤面が完全に一つの数値になったことで適用しやすくなったアルゴリズムは多いので、実は思った以上の恩恵があるんですよねコレ。

以降はこの圧縮した盤面表現を使っていきます。

重複盤面チェックの高速化

これまでのプログラムを実行してみて気づいた方おられるかもしれませんが、盤面の列挙をしていると最初は調査した盤面数はかなり早く増えるのに対し、既に調査した盤面数が多くなればなるほど調査が遅くなってきます。
それもそのはず、新たに盤面を列挙する際その盤面が過去に既に列挙されたかを調べるので、後に列挙する盤面の方が照合する盤面数が多いため、チェックに時間がかかってきてしまうのです。

聞いた事がある人居るかもしれませんが、大体プログラム中で重いところってのはループの中のループで、今回の例で言うとちょうど盤面調査のループの中の、過去の盤面との照合ループだったりします。
ここを何とか高速化すれば列挙した盤面数が増えても列挙の速度をそこまで下がらなくなり、結果として全体の高速化が望めそうです。

そして盤面の重複チェックですが、前節の盤面表現の圧縮により盤面が配列ではなく値になったため、要するにある値が配列中にあるかないかを高速に判定することど同じです。
ここで”そういえば聞いたことがある…”ってなる人が中級者の方には多そうですが、今回のケースではそのものズバリ二分探索が適用可能です。

二分探索ではソート済みの配列が必要になってくるので、今回の8パズルに適用するに当たって、盤面保存用の配列はそのままに、ソート済みの盤面保存用配列を別に作っておきます。
これは盤面重複チェック高速化のためだけのもので、それだけのためにメモリを使うのも忍びない気もしますが、今は高速化のために心を鬼にします。

さてこの盤面重複チェック用の配列ですが、列挙の度に要素が追加されるという状況の中、常にソートされた状態を維持する必要があります。
追加してソート、という手もあるのですが流石にそれは早くならないと思われるので、今回は二分挿入ソートという手法を使います。
二分探索で重複チェックし、かつその位置に挿入を行うという感じですね、無駄がなさそう。

二分探索を使った盤面重複高速化
#include "winmm.as"

#module
// 盤面の描画
// 起点X, 起点Y, 盤面配列, 描画サイズ
#deffunc drawBoard int cx, int cy, int board, int size
    bsz = size*3

    // 背景（下地）のクリア
    color 255, 255, 255 : boxf cx, cy, cx+bsz, cy+bsz

    // 枠線
    color 0, 0, 0
    repeat 4
        ofs = cnt*size
        line cx, cy+ofs, cx+bsz, cy+ofs
        line cx+ofs, cy, cx+ofs, cy+bsz
    loop
    // 駒
    font msgothic, size
    repeat 9
        cntXP3S = cx + cnt\3 * size
        cntXD3S = cy + cnt/3 * size
        color 0, 0, 0 : pos cntXP3S+size/4, cntXD3S
        if ( nth(board, cnt) != 0 ) {// 空白じゃないなら
            mes ""+nth(board, cnt)
        }
    loop
return

// 盤面のインデックスからその駒を返す
#defcfunc nth int board, int idx
    if ( idx >= 8 ) {
        sum = 0
        repeat 8
            sum += nth(board, cnt)
        loop
        return 36 - sum
    }
return ( board >> (idx*4) ) & 0x0f

// 駒とインデックスから盤面のint表現での値を返す
#defcfunc toNth int value, int idx
    if ( idx >= 8 ) : return 0
return ( value & 0x0f ) << (idx*4)

// 9つの駒を受け取って盤面を返す
#defcfunc makeBoard int p1, int p2, int p3, int p4, int p5, int p6, int p7, int p8, int p9
return toNth(p1,0)+toNth(p2,1)+toNth(p3,2)+toNth(p4,3)+toNth(p5,4)+toNth(p6,5)+toNth(p7,6)+toNth(p8,7)// p9は使わない

// 盤面の中で空白のインデックスを返す
#defcfunc searchEmpty int board, local res
    res = -1
    repeat 9
        if ( nth(board, cnt) ) : continue
        res = cnt
        break
    loop
return res

// 盤面の中の2つの要素位置を交換し、その盤面を返す
#defcfunc swapPiece int board, int piece1, int piece2, local t
    n1 = nth(board, piece1) : n2 = nth(board, piece2)
return board - toNth(n1, piece1) - toNth(n2, piece2) + toNth(n1, piece2) + toNth(n2, piece1)
#global

// 盤面保存のための配列
dim storedBoards, 181440// 9!/2
dim storedBoardSteps, 181440// 何手目で辿り着いたか
dim sortedBoards, 181440// ソート済み盤面保存配列
storedBoardNum = 0// いくつ保存しているか
popedBoardNum = 0// 保存した盤面のうち、いくつ既に調べたか（更に列挙したか）

// 最初の盤面を、”誰かから列挙された”として追加
board = makeBoard( 0, 1, 2, 3, 4, 5, 6, 7, 8 )
drawBoard 10, 10, board, 40

storedBoards(storedBoardNum) = board
storedBoardSteps(storedBoardNum) = 0// 最初の盤面は、0手で辿り着いた、とする
sortedBoards(storedBoardNum) = board
storedBoardNum++

// 目的の盤面
objectiveBoard = makeBoard( 3, 1, 2, 4, 7, 5, 6, 0, 8 )// 3手
//objectiveBoard = makeBoard( 3, 1, 2, 4, 7, 0, 6, 8, 5 )// 5手
//objectiveBoard = makeBoard( 0, 1, 5, 3, 2, 8, 6, 4, 7 )// 8手
//objectiveBoard = makeBoard( 3, 1, 5, 2, 4, 8, 6, 0, 7 )// 11手
//objectiveBoard = makeBoard( 3, 1, 0, 2, 7, 5, 6, 8, 4 )// 12手
//objectiveBoard = makeBoard( 3, 0, 1, 2, 7, 5, 6, 8, 4 )// 13手
//objectiveBoard = makeBoard( 0, 1, 2, 4, 7, 5, 6, 3, 8 )// 14手
//objectiveBoard = makeBoard( 7, 6, 2, 1, 5, 0, 3, 4, 8 )// 15手
//objectiveBoard = makeBoard( 4, 2, 8, 1, 0, 5, 6, 7, 3 )// 16手
//objectiveBoard = makeBoard( 4, 0, 5, 1, 8, 2, 6, 7, 3 )// 17手
//objectiveBoard = makeBoard( 1, 8, 5, 2, 6, 4, 3, 7, 0 )// 18手
//objectiveBoard = makeBoard( 1, 5, 6, 2, 8, 0, 3, 7, 4 )// 19手
//objectiveBoard = makeBoard( 1, 5, 6, 2, 8, 4, 3, 7, 0 )// 20手
//objectiveBoard = makeBoard( 2, 1, 5, 3, 4, 6, 8, 0, 7 )// 21手
//objectiveBoard = makeBoard( 2, 1, 5, 3, 0, 6, 8, 4, 7 )// 22手
//objectiveBoard = makeBoard( 2, 3, 7, 5, 1, 4, 6, 0, 8 )// 23手
//objectiveBoard = makeBoard( 8, 4, 1, 5, 7, 6, 0, 3, 2 )// 24手
//objectiveBoard = makeBoard( 8, 5, 1, 4, 6, 0, 7, 3, 2 )// 25手
//objectiveBoard = makeBoard( 8, 2, 3, 6, 7, 4, 1, 5, 0 )// 26手
//objectiveBoard = makeBoard( 0, 5, 3, 6, 1, 7, 2, 8, 4 )// 27手
//objectiveBoard = makeBoard( 8, 5, 1, 2, 6, 0, 7, 4, 3 )// 28手
//objectiveBoard = makeBoard( 8, 5, 6, 3, 1, 4, 2, 0, 7 )// 29手
//objectiveBoard = makeBoard( 6, 7, 8, 3, 1, 4, 2, 5, 0 )// 30手
//objectiveBoard = makeBoard( 8, 7, 6, 0, 4, 1, 2, 5, 3 )// 31手（最大）
//objectiveBoard = makeBoard( 8, 0, 6, 5, 4, 7, 2, 3, 1 )// 31手（最大）
drawBoard 180, 10, objectiveBoard, 40

// 開始時間
timeGetTime : st = stat

// 保存した盤面の中で、まだ更に列挙してないものがあったら更に列挙する
repeat
    // もう調べるものはないか？
    if ( popedBoardNum >= storedBoardNum ) : break

    // 調べる盤面として一個取り出す
    board = storedBoards(popedBoardnum)
    boardRequiredStepNum = storedBoardSteps(popedBoardnum)// 何手目でこの盤面は得られるか
    popedBoardnum++

    // 目的の盤面かチェック
    isObjectiveBoard = ( board == objectiveBoard )
    if ( isObjectiveBoard ) {
        break
    }

    // 空白の配列インデックスを取得
    emptyIdx = searchEmpty( board )

    // 盤面中の空白のx位置、y位置　：左上を(0,0)、右下を(2.2)とする
    emptyX = emptyIdx \3
    emptyY = emptyIdx /3

    // 上下左右の駒と交換できるなら交換した盤面を列挙する
    repeat 4
        // 列挙する盤面
        // とりあえず元のをコピー
        newBoard = board
        // 上下左右、どこに移動するか
        dx = 0 : dy = 0 : label=""
        switch( cnt )
            case 0 : dx =  0 : dy = -1 : label="上" : swbreak// 上
            case 1 : dx =  0 : dy =  1 : label="下" : swbreak// 下
            case 2 : dx =  1 : dy =  0 : label="右" : swbreak// 右
            case 3 : dx = -1 : dy =  0 : label="左" : swbreak// 左
        swend
        // 交換する駒のx位置、y位置
        swapX = emptyX + dx
        swapY = emptyY + dy
        // 交換する駒の位置が範囲外なら何もしない
        if ( swapX<0 || swapX>=3 || swapY<0 || swapY>=3 ) {
            continue
        }
        // 交換する駒の位置の配列インデックス
        swapIdx = swapX + swapY *3
        // 駒の交換
        newBoard = swapPiece( newBoard, emptyIdx, swapIdx )

        // 既に保存した盤面か調べる、二分探索
        searchLeft = 0 : searchRight = storedBoardNum
        repeat 32// この回数は適当、2^32の数（uintで表現可能な範囲）まで対応可能なので、大丈夫なハズ
            if ( searchLeft >= searchRight ) : break
            peekBoardIdx = (searchLeft + searchRight) /2
            if ( sortedBoards(peekBoardIdx) <= newBoard ) {
                searchLeft = peekBoardIdx +1
            } else {
                searchRight = peekBoardIdx
            }
        loop

        if ( searchLeft <= 0 ) {
            isAlreadySearched = 0
        } else {
            isAlreadySearched = ( sortedBoards(searchLeft -1) == newBoard )
        }

        // 既に保存した盤面だったら何もしないで次へ
        if ( isAlreadySearched ) : continue

        // 列挙した盤面の保存、もう保存できなかったら何もしない
        if ( storedBoardNum < length( storedBoards ) ) {
            storedBoards(storedBoardNum) = newBoard
            storedBoardSteps(storedBoardNum) = boardRequiredStepNum+1// 自分の盤面＋１
            // ソート挿入、1要素後ろにずらす
            memcpy sortedBoards, sortedBoards, (storedBoardNum -searchLeft) *4, (searchLeft+1) *4, (searchLeft) *4
            sortedBoards(searchLeft) = newBoard
            storedBoardNum++
        }
    loop

    // 適当にwaitをいれる
    if ( (popedBoardnum\500) == 0 ) {
        title "調べた盤面数　：　"+popedBoardnum
        await 0
    }
loop

// かかった時間
timeGetTime : ed = stat
delta = ed -st

color 0, 0, 0 : pos 10, 200 : font msgothic, 20
mes "手数　：　"+boardRequiredStepNum
mes "かかった時間　＝　"+(delta)+"ミリ秒"
mes "列挙した盤面数　＝　"+(storedBoardNum)
mes "調べた盤面数　＝　"+(popedBoardnum)

そして結果。

手数 時間（ミリ秒） 参考：元の時間（ミリ秒） 列挙した盤面数 調べた盤面数
3 0 0 19 10
5 1 2 63 38
8 5 40 394 252
11 28 671 1737 1043
12 44 1744 2791 1791
13 69 4584 4613 2792
14 94 7209 5706 3575
15 135 18602 8934 5678
16 289 58894 15887 10544
17 445 144159 25207 16317
18 663 --- 34494 23944
19 794 --- 39933 28205
20 1210 --- 57107 39935
21 2172 --- 88259 66076
22 3060 --- 110116 88260
23 4261 --- 138967 115001
24 4843 --- 150221 130921
25 5700 --- 165778 150176
26 6138 --- 171237 157464
27 6467 --- 176437 169824
28 6815 --- 180451 176534
29 6924 --- 181341 180773
30 6922 --- 181440 181333
31 6924 --- 181440 181440

劇的に早くなりました、もうこれでいい気がしてきちゃいますね。
早くなったのでテストケースも増やしておきました、ここに載せた分で最長手数が解けており、しかもまだ現実的な時間に収まっています。3
表を見るとわかりますが、後半は調査盤面数が順調に増える一方、列挙盤面数は頭打ちに近づいています。

探索の改良

前節までで列挙した盤面数が増えてもそこまで速度低下せずに列挙が続けられるようになりました。
ただ、結果の表を見たところ、列挙盤面数は頭打ちにまできていますが最小手数の増加に伴って列挙した盤面及び調査した盤面が膨大な数になっていっているのが確認できます。
二分探索自体数に対してかなり強い手法なので、現状でこの処理速度は最早列挙してる盤面数が多すぎることが原因だと考えるのが妥当です。
まぁ、最大ケースが$181440$個で、それが10秒もかからず求まっているのだからこのままでいいじゃん、という気持ちもありつつ、本節では列挙する盤面数を少なくする方法を考えていきましょう。

手数による盤面数の爆発

既に何度も述べましたが、今までは最初の盤面から、1手で得られる盤面を列挙するという方法で目的の盤面まで辿り着くかを見ていました。
この1手で得られる盤面を列挙する、ですが、よくよく考えると特定の盤面から1手で得られる盤面は4つ、そしてその盤面から更に得られる盤面は4つなので全部で16、そしてその盤面から得られる盤面は…と、爆発的に増えていくことが分かります。（実際は重複分を避けるし、列挙できるのは2だけだったりとかもあるので、こんなことにはならないんですが）
$N$手先の盤面の数は、過大評価して高々見積もると$4^N$になります。

最初の盤面からの列挙、最後の盤面からの列挙

でも、この数字は$N$手先と、手数に依存しています。
ならば、この手数を少なくすれば数は減ります、当たり前ですよね？

ここで偉い人は考えました。

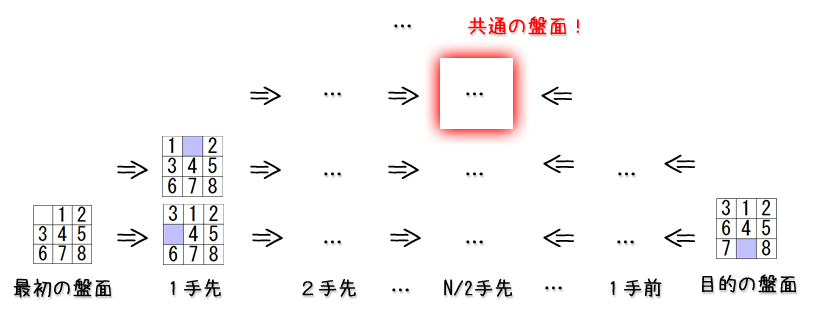
最初の盤面と最後の盤面から同時に列挙を行ったらどうだろう。

辿り着くかどうかの判定は、列挙された盤面が”最初の盤面から”なのか、”最後の盤面から”なのかを覚えておき、それが異なった盤面からだったら辿り着くとする、というものです。
こうすると、”最初の盤面”から”最後の盤面”までの最小手数が$N$だった場合、”最初の盤面”からの列挙と”最後の盤面”からの列挙が$N/2$手先まで列挙してしまえば共通の盤面が見つかりそうです。
つまり、今までは”最初の盤面”からの列挙のみで$4^N$必要だったのが、”最初の盤面”と”最後の盤面”からの$N/2$手先なので$2*4^{N/2}$で済むことになりそうです。

偉い人、スゴイ。

図で描くと

こうではなく
puzzle8_forwardSearchSolution.png

こうじゃ
puzzle8_bidirectionalSolution.png

コードに落とす

方針は決まったので後はやるだけなんですが、HSP中級者の方はもうどういうコード書くべきか見えていると思いますので説明は端折ます。
いくつかやり方あると思いますが、個人で解けているならもうそれでいいと思います。4

私は、”盤面が最初の盤面と最後の盤面どちらから列挙されたか”の配列と、”ソート済み盤面配列の要素から、元の盤面保存用の配列でのインデックスを保持する”配列の2つを使って実装しました。
この双方向探索の実装、微妙に難易度高かったので腕に覚えがある人にはオススメ！！

双方向探索と二分探索重複チェックの高速化を施した8パズル解く君
#include "winmm.as"

#module
// 盤面の描画
// 起点X, 起点Y, 盤面配列, 描画サイズ
#deffunc drawBoard int cx, int cy, int board, int size
    bsz = size*3

    // 背景（下地）のクリア
    color 255, 255, 255 : boxf cx, cy, cx+bsz, cy+bsz

    // 枠線
    color 0, 0, 0
    repeat 4
        ofs = cnt*size
        line cx, cy+ofs, cx+bsz, cy+ofs
        line cx+ofs, cy, cx+ofs, cy+bsz
    loop
    // 駒
    font msgothic, size
    repeat 9
        cntXP3S = cx + cnt\3 * size
        cntXD3S = cy + cnt/3 * size
        color 0, 0, 0 : pos cntXP3S+size/4, cntXD3S
        if ( nth(board, cnt) != 0 ) {// 空白じゃないなら
            mes ""+nth(board, cnt)
        }
    loop
return

// 盤面のインデックスからその駒を返す
#defcfunc nth int board, int idx
    if ( idx >= 8 ) {
        sum = 0
        repeat 8
            sum += nth(board, cnt)
        loop
        return 36 - sum
    }
return ( board >> (idx*4) ) & 0x0f

// 駒とインデックスから盤面のint表現での値を返す
#defcfunc toNth int value, int idx
    if ( idx >= 8 ) : return 0
return ( value & 0x0f ) << (idx*4)

// 9つの駒を受け取って盤面を返す
#defcfunc makeBoard int p1, int p2, int p3, int p4, int p5, int p6, int p7, int p8, int p9
return toNth(p1,0)+toNth(p2,1)+toNth(p3,2)+toNth(p4,3)+toNth(p5,4)+toNth(p6,5)+toNth(p7,6)+toNth(p8,7)// p9は使わない

// 盤面の中で空白のインデックスを返す
#defcfunc searchEmpty int board, local res
    res = -1
    repeat 9
        if ( nth(board, cnt) ) : continue
        res = cnt
        break
    loop
return res

// 盤面の中の2つの要素位置を交換し、その盤面を返す
#defcfunc swapPiece int board, int piece1, int piece2, local t
    n1 = nth(board, piece1) : n2 = nth(board, piece2)
return board - toNth(n1, piece1) - toNth(n2, piece2) + toNth(n1, piece2) + toNth(n2, piece1)
#global

// 盤面保存のための配列
dim storedBoards, 181440// 9!/2
dim storedBoardSteps, 181440// 何手目で辿り着いたか
dim storedBoardFrom, 181440// 最後の盤面から生成されたら1、そうでないなら0
dim sortedBoards, 181440// ソート済み盤面保存配列
dim sortedBoardIdx, 181440// ソート済み、storedBoardsのインデックスを保持
storedBoardNum = 0// いくつ保存しているか
popedBoardNum = 0// 保存した盤面のうち、いくつ既に調べたか（更に列挙したか）

// 最初の盤面を、”誰かから列挙された”として追加
board = makeBoard( 0, 1, 2, 3, 4, 5, 6, 7, 8 )
drawBoard 10, 10, board, 40

storedBoards(storedBoardNum) = board
storedBoardSteps(storedBoardNum) = 0// 最初の盤面は、0手で辿り着いた、とする
storedBoardFrom(storedBoardNum) = 0
sortedBoards(storedBoardNum) = board
sortedBoardIdx(storedBoardNum) = storedBoardNum
storedBoardNum++

// 目的の盤面も、”誰かから列挙された”として追加
objectiveBoard = makeBoard( 3, 1, 2, 4, 7, 5, 6, 0, 8 )// 3手
//objectiveBoard = makeBoard( 3, 1, 2, 4, 7, 0, 6, 8, 5 )// 5手
//objectiveBoard = makeBoard( 0, 1, 5, 3, 2, 8, 6, 4, 7 )// 8手
//objectiveBoard = makeBoard( 3, 1, 5, 2, 4, 8, 6, 0, 7 )// 11手
//objectiveBoard = makeBoard( 3, 1, 0, 2, 7, 5, 6, 8, 4 )// 12手
//objectiveBoard = makeBoard( 3, 0, 1, 2, 7, 5, 6, 8, 4 )// 13手
//objectiveBoard = makeBoard( 0, 1, 2, 4, 7, 5, 6, 3, 8 )// 14手
//objectiveBoard = makeBoard( 7, 6, 2, 1, 5, 0, 3, 4, 8 )// 15手
//objectiveBoard = makeBoard( 4, 2, 8, 1, 0, 5, 6, 7, 3 )// 16手
//objectiveBoard = makeBoard( 4, 0, 5, 1, 8, 2, 6, 7, 3 )// 17手
//objectiveBoard = makeBoard( 1, 8, 5, 2, 6, 4, 3, 7, 0 )// 18手
//objectiveBoard = makeBoard( 1, 5, 6, 2, 8, 0, 3, 7, 4 )// 19手
//objectiveBoard = makeBoard( 1, 5, 6, 2, 8, 4, 3, 7, 0 )// 20手
//objectiveBoard = makeBoard( 2, 1, 5, 3, 4, 6, 8, 0, 7 )// 21手
//objectiveBoard = makeBoard( 2, 1, 5, 3, 0, 6, 8, 4, 7 )// 22手
//objectiveBoard = makeBoard( 2, 3, 7, 5, 1, 4, 6, 0, 8 )// 23手
//objectiveBoard = makeBoard( 8, 4, 1, 5, 7, 6, 0, 3, 2 )// 24手
//objectiveBoard = makeBoard( 8, 5, 1, 4, 6, 0, 7, 3, 2 )// 25手
//objectiveBoard = makeBoard( 8, 2, 3, 6, 7, 4, 1, 5, 0 )// 26手
//objectiveBoard = makeBoard( 0, 5, 3, 6, 1, 7, 2, 8, 4 )// 27手
//objectiveBoard = makeBoard( 8, 5, 1, 2, 6, 0, 7, 4, 3 )// 28手
//objectiveBoard = makeBoard( 8, 5, 6, 3, 1, 4, 2, 0, 7 )// 29手
//objectiveBoard = makeBoard( 6, 7, 8, 3, 1, 4, 2, 5, 0 )// 30手
//objectiveBoard = makeBoard( 8, 7, 6, 0, 4, 1, 2, 5, 3 )// 31手（最大）
//objectiveBoard = makeBoard( 8, 0, 6, 5, 4, 7, 2, 3, 1 )// 31手（最大）
drawBoard 180, 10, objectiveBoard, 40

storedBoards(storedBoardNum) = objectiveBoard
storedBoardSteps(storedBoardNum) = 0// 最後の盤面も、0手で辿り着いた、とする
storedBoardFrom(storedBoardNum) = 1
if ( board < objectiveBoard ) {
    sortedBoards(storedBoardNum) = objectiveBoard
    sortedBoardIdx(storedBoardNum) = storedBoardNum
} else {
    sortedBoards(storedBoardNum -1) = objectiveBoard
    sortedBoards(storedBoardNum) = board
    sortedBoardIdx(storedBoardNum -1) = storedBoardNum
    sortedBoardIdx(storedBoardNum) = storedBoardNum -1
}
storedBoardNum++

// 開始時間
timeGetTime : st = stat

// 最小手数
minStepNum = -1

// 保存した盤面の中で、まだ更に列挙してないものがあったら更に列挙する
repeat
    // もう調べるものはないか？
    if ( popedBoardNum >= storedBoardNum ) : break

    // 調べる盤面として一個取り出す
    board = storedBoards(popedBoardNum)
    boardRequiredStepNum = storedBoardSteps(popedBoardNum)// 何手目でこの盤面は得られるか
    isBoardFromObjective = storedBoardFrom(popedBoardNum)
    popedBoardNum++

    // 空白の配列インデックスを取得
    emptyIdx = searchEmpty( board )

    // 盤面中の空白のx位置、y位置　：左上を(0,0)、右下を(2.2)とする
    emptyX = emptyIdx \3
    emptyY = emptyIdx /3

    // 上下左右の駒と交換できるなら交換した盤面を列挙する
    repeat 4
        // 列挙する盤面
        // とりあえず元のをコピー
        newBoard = board
        // 上下左右、どこに移動するか
        dx = 0 : dy = 0 : label=""
        switch( cnt )
            case 0 : dx =  0 : dy = -1 : label="上" : swbreak// 上
            case 1 : dx =  0 : dy =  1 : label="下" : swbreak// 下
            case 2 : dx =  1 : dy =  0 : label="右" : swbreak// 右
            case 3 : dx = -1 : dy =  0 : label="左" : swbreak// 左
        swend
        // 交換する駒のx位置、y位置
        swapX = emptyX + dx
        swapY = emptyY + dy
        // 交換する駒の位置が範囲外なら何もしない
        if ( swapX<0 || swapX>=3 || swapY<0 || swapY>=3 ) {
            continue
        }
        // 交換する駒の位置の配列インデックス
        swapIdx = swapX + swapY *3
        // 駒の交換
        newBoard = swapPiece( newBoard, emptyIdx, swapIdx )

        // 既に保存した盤面か調べる、二分探索
        searchLeft = 0 : searchRight = storedBoardNum
        repeat 32// この回数は適当、2^32の数（uintで表現可能な範囲）まで対応可能なので、大丈夫なハズ
            if ( searchLeft >= searchRight ) : break
            peekBoardIdx = (searchLeft + searchRight) /2
            if ( sortedBoards(peekBoardIdx) <= newBoard ) {
                searchLeft = peekBoardIdx +1
            } else {
                searchRight = peekBoardIdx
            }
        loop

        if ( searchLeft <= 0 ) {
            isAlreadySearched = 0
        } else {
            isAlreadySearched = ( sortedBoards(searchLeft -1) == newBoard )
        }

        // 既に保存した盤面だったら
        if ( isAlreadySearched ) {
            pastBoardIdx = sortedBoardIdx(searchLeft -1)
            if ( isBoardFromObjective != storedBoardFrom(pastBoardIdx) ) {
                // 見つかった盤面の出自が違うなら、共通盤面が見つかったことになるのでここで探索終了
                minStepNum = boardRequiredStepNum + storedBoardSteps(pastBoardIdx) +1
                break
            }

            // 何もしないで次へ
            continue
        }

        // 列挙した盤面の保存、もう保存できなかったら何もしない
        if ( storedBoardNum < length( storedBoards ) ) {
            storedBoards(storedBoardNum) = newBoard
            storedBoardSteps(storedBoardNum) = boardRequiredStepNum+1// 自分の盤面＋１
            storedBoardFrom(storedBoardNum) = isBoardFromObjective// 出自は一緒
            // ソート挿入、1要素後ろにずらす
            memcpy sortedBoards, sortedBoards, (storedBoardNum -searchLeft) *4, (searchLeft+1) *4, (searchLeft) *4
            sortedBoards(searchLeft) = newBoard
            memcpy sortedBoardIdx, sortedBoardIdx, (storedBoardNum -searchLeft) *4, (searchLeft+1) *4, (searchLeft) *4
            sortedBoardIdx(searchLeft) = storedBoardNum
            storedBoardNum++
        }
    loop

    // もう見つかった
    if ( minStepNum >= 0 ) : break

    // 適当にwaitをいれる
    if ( (popedBoardnum\500) == 0 ) {
        title "調べた盤面数　：　"+popedBoardnum
        await 0
    }
loop

// かかった時間
timeGetTime : ed = stat
delta = ed -st

color 0, 0, 0 : pos 10, 200 : font msgothic, 20
mes "手数　：　"+minStepNum
mes "かかった時間　＝　"+(delta)+"ミリ秒"
mes "列挙した盤面数　＝　"+(storedBoardNum)
mes "調べた盤面数　＝　"+(popedBoardnum)

そして結果。

手数 時間（ミリ秒） 列挙した盤面数 調べた盤面数 参考：元の時間（ミリ秒） 参考：元の列挙した盤面数 参考：元の調べた盤面数
3 0 8 3 0 19 10
5 0 18 9 2 63 38
8 1 54 27 40 394 252
11 1 143 81 671 1737 1043
12 2 145 85 1744 2791 1791
13 3 250 147 4584 4613 2792
14 3 279 165 7209 5706 3575
15 4 376 215 18602 8934 5678
16 6 549 323 58894 15887 10544
17 9 678 430 144159 25207 16317
18 10 774 489 --- 34494 23944
19 18 943 577 --- 39933 28205
20 21 1265 763 --- 57107 39935
21 29 1711 1083 --- 88259 66076
22 35 2252 1419 --- 110116 88260
23 46 3085 1843 --- 138967 115001
24 54 3490 2094 --- 150221 130921
25 68 4361 2752 --- 165778 150176
26 85 5345 3398 --- 171237 157464
27 78 4864 3048 --- 176437 169824
28 129 8130 4893 --- 180451 176534
29 172 10137 6391 --- 181341 180773
30 221 12107 7689 --- 181440 181333
31 274 15880 10021 --- 181440 181440

また劇的に早くなりました。
列挙した盤面数と、調査した盤面数がそもそもかなり少なくなっているのも確認できますね、狙い通りです。
これでもう”8パズル解いて、ちょっぱやで！”とか言われても何とかなりそうですね。5

おわりに

以上、HSPで8パズルを題材にした（主に幅優先）探索の話でした。
AdventCalendarですが軽いお菓子ばっかりではなく、たまには消化に時間がかかるお菓子でも良いのではと思って投稿しました、読み切った方いらっしゃったらお疲れ様です。
この手のアルゴリが使えるとなんやかんや出来るようになる訳ですが、私の経験則だとHSP触ってる時って実際こういうなんやかんやって必要なケース少ない気がするんですよね。

…私がそういうのをあんまり作ってなかっただけかも。

それでも、こういった話はプログラム書いてる限りはどこかで付きまとわれる話なので、そういった人の助けにでもなれば幸いです。

なんやかんや補足とか

今回試してないけど他のトピックとしてはA*（とか双方向A*）とか、そもそも幅優先じゃなくて深さ優先探索（＋反復深化）とか、枝刈りちゃんとしようねとか、二分探索じゃなくてN分木（駒の種類が9種類なので、9分木）使った方が$O(log_9 N)$まで落とせるとか、色々あります。6
アルゴリズムの話の外も見ればマルチスレッドとかも見えてきますね。
そして盤面の圧縮だと今回は4ビット単位に詰め込んだけど、よくよく考えたら9進法使うとか、最小完全ハッシュ使ってもよかったんじゃないか、と振り返って思いました、書いてる時は案外気付かないんだよね。

そういうの突っ込み始めるとこの記事がどこに向かっているのか分からなくなるのでやりませんでしたが、それらの話自体は難しくはありません。
こんな記事だけじゃ満足できない！とかそういうのがやりたかったんだよ俺は！という猛者の方はチャレンジしてみると面白いのではないでしょうか。
確かA*は既に手垢ついてた記憶あるので、亜種の双方向A*とかHSPでは未踏の地だから誰かそういうのを！（無茶振り）

それでは！

  1. 読んでる方も大変なんでしょうが、書いてる方って基本思われている以上に大変なのよね、それが世の常。 ↩

  2. ちなみにここまで書くのに筆者がかかった時間およそ6時間、筆者がヒーヒー言い始める時間。 ↩

  3. ちなみにちなみにここまで書くのに筆者がかかった時間およそ10時間、筆者がハヒーハヒー言ってる時間。これぐらい時間かけたら31手も解けてるのかな…。 ↩

  4. ちなみにちなみにちなみにここまで書くのに筆者がかかった時間およそ13時間、筆者のテンションが下がって投げやりになってきている頃。 ↩

  5. ちなみにちなみにちなみにちなみになんですが、ここまで書くのに筆者がかかった時間およそ15時間、かなり疲れた。 ↩

  6. A*も盤面の列挙数を抑える方向の手法なので、実は双方向探索と同じような効果な気がしてます。使用するヒューリスティックによって結果は変わるだろうけど、基本的にA*のが賢いのでより良い結果がでるでしょうね。でもA*、プライオリティーキューが必要な気がして、HSPでの実装はかなり重めだよな…。 ↩

10
6
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
10
6