マンデルブロ集合の３次元への拡張が見たい！

##はじめに
マンデルブロ集合は、２次元で画像表現したときに拡大しても同じパターンが現れる（フラクタル）図形として有名です。
数学者ブノワ・マンデルブロの名前を取って数学者エイドリアン・ドゥアディが命名しました。

How to use the OpenCV parallel_for_ to parallelize your codeより画像を引用。白い縁取りの内側にある黒い領域がマンデルブロ集合に該当する領域。

とても美しい図形だと筆者は思います。
マンデルブロ集合に興味を持たれた方は@ryunryunryunさんの愛おしすぎるMandelbrot集合をProcessingで描くをご覧ください。わかりやすい解説とコードがあります。描画方法を理解した上で画像を見るとマンデルブロ集合の魅力が増加すると思います。
本記事は上記@ryunryunryunさんの記事とコード、およびOpenCVのparallel_for_()関数のチュートリアルを要約した拙作OpenCV(C++)チュートリアル：parallel_for_でコードを並列化する（マンデルブロ集合）をもとにして執筆しています。

###本記事の概要
本記事のテーマは、通常２次元画像として表現されるマンデルブロ集合を、3次元の立体として表現できないかということです。
後述のようにマンデルブロ集合は複素数を用いて定義され、実軸と虚軸をx, y座標にマッピングすることで２次元画像の表現を得ます。

３次元(３軸)で定義可能なマンデルブロ集合は複素数による定義にならないと予想されるため、おそらくもうマンデルブロ集合とは呼べませんが、３次元立体としてマンデルブロ集合っぽいもので、かつ数学的にも納得いくような表現を見たい！というのが筆者のモチベーションです。

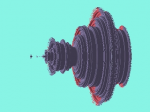
こんなかんじかな？

当然ですが、先行研究が存在します。
中でも著しいのはDaniel Whiteらによるマンデルバルブと呼ばれるもので、１０年ほど前に発表されています。
先行研究については後述します。

##マンデルブロ集合の定義

定義式をwikipediaの記事から引用すると

次の漸化式

\left\{
\begin{array}{ll}
Z_{n+1} = Z_n^2 + c \\
Z_0 = 0
\end{array}
\right.

で定義される複素数列{$Z_n$} $n\in N \cup$ {$0$}が $n\rightarrow \infty$の極限で無限大に発散しないという条件を満たす複素数 $c$ 全体が作る集合がマンデルブロ集合である。

となります。
つまり、はじめに複素数cを選び、それとは別の複素数$z_0=0$から開始して、上記の漸化式の計算を繰り返し、どんなにnが大きくなっても$z_n$の絶対値が発散しなければ、その複素数cはマンデルブロ集合に含まれる、というものです。
この漸化式は後で式(*)として使います。

###定義の使い方
上記のどんなにnが大きくなっても$z_n$の絶対値が発散しなければという条件は、次の式で表現されます。

\limsup_{n\to\infty} |z_{n+1}| \leq 2 \tag{1}

左辺の$|\cdot|$は絶対値で、一般に複素数$z=a+bi$の絶対値は

|z|=\sqrt{a^2+b^2} \tag{2}

で定義されます。

マンデルブロ集合を定義する漸化式

\left\{
\begin{array}{ll}
Z_{n+1} = Z_n^2 + c \\
Z_0 = 0
\end{array}
\right.
\tag{*}

において、cは複素数ですので実部と虚部の２要素を持ちます。つまり

c=x+yi \tag{3}

と表せます。
このxとyには適切なスケールに変換された画像の座標が入ります。

####漸化式()の展開
式()において、n=0の時$Z_0$=0ですので、

\begin{align}
Z_{0+1} &= 0^2 + c \\
&=c \\
&=x+yi
\end{align}

となります。
１行目から２行目へは式(3)$c=x+yi$を使いました。
次のn=1では、

\begin{align}
Z_{1+1} &= (x+yi)^2 + c \\
&= x^2 + 2xyi - y^2 + c \\
&=x^2 + x - y^2 + 2xyi + yi　\\
&=x^2 + x - y^2 + (2xy + y)i \tag{4}
\end{align}

となります。
この時、右辺の実部は$x^2 + x - y^2$, 虚部は$2xy + y$です。この値を式(2)に代入して、計算に使用した複素数$c$がマンデルブロ集合に属するかどうかを式(1)で判断します。

実用的にはn=無限大まで計算せずに、適当な大きい整数を上限に計算し、上限まで式(1)を満たし続けたピクセルc(x,y)はマンデルブロ集合に属するものとします。escape time algorithmと呼ばれるマンデルブロ集合の判定方法です。

##３次元への拡張
次のように考えました。

• 従来の定義では複素数がx軸、y軸と対応付けられる。
• 描画対象の空間に３番目の軸としてz軸(高さ方向)を付け加える
• 実部、虚部、？部の３つ組で一つの数を表す数を用意して、同様の計算をすれば良い

従来のアルゴリズムから変更の必要がある箇所は次の通りです。

1. 画像はx,yの２次元なので、高さ方向の変数を作ってイテレートする
2. 式(1)の判定で３軸目の項を考慮する
3. 式(4)が示すように、変数の更新時に３軸目の項を考慮する（例えば虚数は２乗すると実数として計算できるが、３軸目の数でも類似の処理が必要かもしれない。）

以降では説明のために３軸目の数をzとして、**式(*)の複素数$Z_n$に対応するものを$W_n$**と呼びます。Wは実部、虚部、？部を持つ数です。つまり,

W=x+yi+zj

です。
ただし$j$は３軸目の要素であることを表します。

###四元数
複素数の拡張として**四元数quaternion（クォターニオン）**が知られています。
四元数は1843年にハミルトンにより劇的な発見をされたことで有名です。興味がある方はwikipediaの記事や、書籍¹等をご覧ください。カッコいいです。

四元数は次のように表されます。wikipediaの記事から引用します。

a + bi + cj + dk

ここで、 a, b, c, d は実数であり、i, j, k は基本的な「四元数の単位」である。

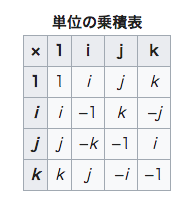
四元数の単位i, j, k については次式が成り立ちます。

```math
i^2=j^2=k^2=ijk=-1

単位i, j, k同士の積は下表のように定義されます。
wikipediaの記事から引用します。

これらは掛ける順番が異なると結果が変わり、例えば$ij=k$ですが、順番を逆にした場合$ji=-k$となります。

###試したこと
改変が必要な箇所を再掲します。

1. 画像はx,yの２次元なので、高さ方向の変数を作ってイテレートする

1. 式(1)の判定で３軸目の項を考慮する
2. 式(4)が示すように、変数の更新時に３軸目の項を考慮する（例えば虚数は２乗すると実数として計算できるが、３軸目の数でも類似の処理が必要かもしれない。）

1は簡単です。forで回すだけです。

2については、複素数の絶対値が2を超えないことがマンデルブロ集合の判定式でした。
判定式(1)を再掲すると、

\limsup_{n\to\infty} |z_{n+1}| \leq 2 \tag{1}

です。
なぜ2なのでしょうか？まだ調べていませんが、今回使用した数$W=x+yi+zj$は絶対値が$|W|=\sqrt{x^2 + y^2 + z^2}$となるよう定義することにしました。したがって、z=0の時、つまり高さがない平面上では従来のマンデルブロ集合と同様の図形が描かれます。

3については、四元数の単位i, j, k同士の積の定義を利用しました。
式(*)を再掲すると、

\left\{
\begin{array}{ll}
Z_{n+1} = Z_n^2 + c \\
Z_0 = 0 \tag{*}
\end{array}
\right.

であり、従来のアルゴリズムでは複素数$Z_n$の２乗を計算する必要があります。拡張アルゴリズムでは数$W_n$の２乗を計算することにします。この計算は四元数の単位同士の積の定義を用いて、

\begin{align}
W_n^2 &=(x+yi+zj)^2 \\
 &=x^2 + y^2ii +z^2jj + 2xyi + 2yzij + 2zxj \\
 &=x^2 - y^2 -z^2 + 2xyi + 2yzk + 2zxj
\end{align}

と展開できます。
最右辺の６個の項を分類すると、

実数　: $x^2 - y^2 -z^2$
虚数(i): $2xyi$
?数(j) : $2zxj$
四元数でkに対応する数: $2yzk$

となります。ただし、最後の四元数でkに対応する数は使用しません。理由は３次元空間には第４の軸がないからです。
漸化式の更新は今計算した$W_n^2$(従来は$Z_n^2$)に数$c$(複素数$c$)を足すことで完了します。つまり拡張された$c$を$c=a+bi+dj$とすると、式(*)より、更新された$W_{n+1}$は

実部: $x^2 - y^2 -z^2 +a$
虚部(i): $2xyi +bi$
?部(j) : $2zxj +dj$

を持つことになります。

##実装
@ryunryunryunさんの記事愛おしすぎるMandelbrot集合をProcessingで描くのコード(processing)を元に、pythonに移植実装しました。
と言っても先述の３つ以外はほぼ変更していません。

import numpy as np
import cv2

w = 800 // 2
h = 700 // 2
depth = 200 // 2 #z軸方向。これは書き出す画像の枚数になる
img = np.ones([h, w, 1]) * 255
iteration = 1000

#画像のピクセルを適切なスケールに変換する
#real
re_min = -2
re_max = 0.7
#imagi
im_min = (re_min - re_max) * h / w / 2.0
im_max = -im_min
#quart 
q_min = int(im_min * 1.6)
q_max = int(im_max * 1.6)

print(im_min, im_max)

#マンデルブロ集合に属するか判定する
def is_in_mandelbrot(a, b, d):
  x = 0
  y = 0
  z = 0
  prev_x = x
  prev_y = y
  prev_z = z
  
  for i in range(iteration):
    cond = x ** 2 + y ** 2 + z ** 2
    if cond >= 4:
      return -i
    
    else:
      prev_x = x
      prev_y = y
      prev_z = z
      x = next_x(prev_x, prev_y, prev_z, a)
      y = next_y(prev_x, prev_y, prev_z, b)
      z = next_z(prev_x, prev_y, prev_z, d)
      
  return 1

#数Wの更新用
def next_x(x, y, z, a):
  ret = x ** 2 - y ** 2 - z ** 2  + a
  return ret

def next_y(x, y, z, b):
  ret = 2 * x * y + b
  return ret 

def next_z(x, y, z, d):
  ret = 2 * z * x  + d 
  return ret

#範囲を変換する関数
def _map(a,b,c,d,e): # map a from b-c to d-e
  b_c = abs(b - c)
  d_e = abs(d - e)
  prop = a / b_c
  x = prop * d_e + d
  
  return x
  
#描画開始
for z in range(depth):
  for i in range(h):
    for j in range(w):
      a = _map(j, 0, w, re_min, re_max)
      b = _map(i, 0, h, im_min, im_max)
      d = _map(z, 0, depth, q_min, q_max)
      ret = is_in_mandelbrot(a, b, d)
      if ret == 1:
          color = 0
      else:
        color = _map(-ret, 0, iteration * 0.1, 255, 0)
      img[i, j] = color
      
  font = cv2.FONT_HERSHEY_SIMPLEX
  cv2.putText(img, str(d), (w-100, h-20), font, 0.75, (150, 150, 150), 1, cv2.LINE_AA)
  name = "{0:04d}".format(z)
  cv2.imwrite("out/{}.png".format(name), img)

###実行
google colab(python3)で実行しました。
実行する前に出力先ディレクトリを作ります。
!mkdir out

実行するとout以下に0000.pngのような画像がたくさんできます。これらの画像は３次元の集合を高さ方向でスライスした断面画像となります。
番号が若いほうが３次元空間の下側です。

##結果

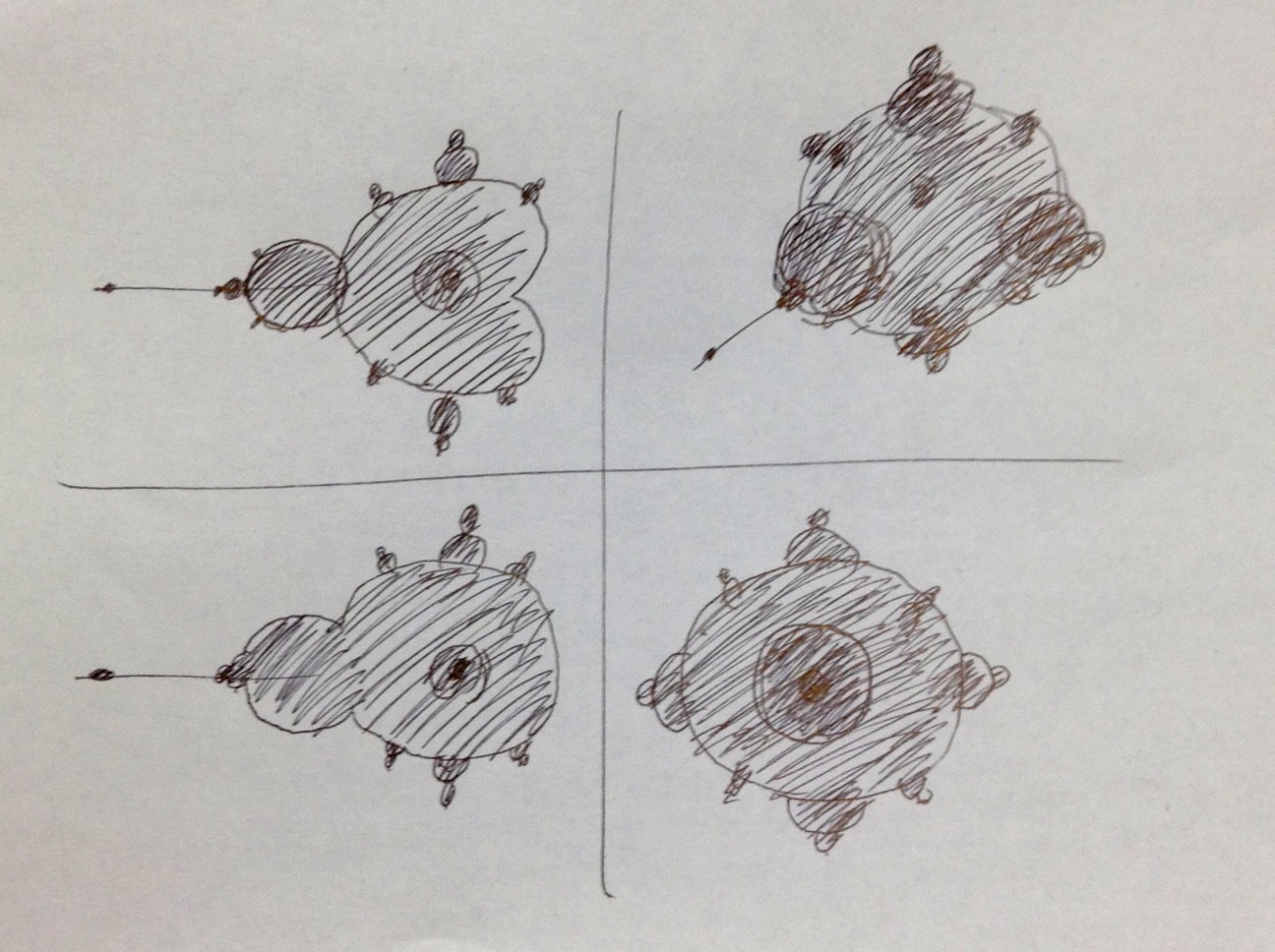
右下の数値は空間内の高さ(コードではforの変数d)を示し、スライスは３次元空間の下から上方向に上昇しています。
ちょうど真ん中の画像(高さ=0に対応する)が、見慣れたマンデルブロ集合になっています。

いかがでしょうか。割とそれっぽいオブジェクトになっている気がします。
しかし、筆者の想像(はじめの方にあるスケッチ参照)と異なるのは、周囲の小さい突起たちが高さの変化と共になめらかにスライドしていくところです。なめらかに収縮ではなく、なめらかにスライドするということは、中心部分の大きな円（球）に沿って同じ形が高さ方向に続いているということです。例えるならばなるとです。中心の球体の周囲に、高さ方向に長い、小突起型の断面をしたなると状の物体が巻き付いているようなイメージとなります。もっとボツボツとくっついているものだと想像していました。
もう一つ気になるのが、集合の周囲に見える微細な黒点（本体と連結していない）です。特に右下の数値近くの黒点はだいたいどの高さの画像でも示されています。高さ=0でも。これはおかしいので、どこかにミスがあるかもしれません。
拡大したときにフラクタル構造を持っているかなど、確認しなければならないことがたくさんありそうです。

##先行研究
おそらく３次元のマンデルブロ集合として最も有力なのは、マンデルバルブと呼ばれるものだと思います。
The Mandelbulb: first 'true' 3D image of famous fractalによると、イギリスのアマチュアフラクタル画像作家**Daniel White**により2007年に発表されました。彼とFractal Forumsは研究を続け、その後2009年にメンバーの一人Paul Nylanderにより改良版が示されています。

マンデルバルブ(改良版：次数8) Paul Nylanderによる。Daniel WhiteのウェブサイトSkytopia内、[The Unravelling of the Real 3D Mandelbulb](http://www.skytopia.com/project/fractal/mandelbulb.html)より引用。

マンデルバルブのギャラリーで詳細な画像が見られます。

マンデルブロ集合を３次元に拡張する試みはこれ以前から行われており、Daniel WhiteによりThe Mystery of the REAL, 3D Mandelbrot Fractalにまとめられています。これによると、彼以前の多くの(全ての)先行研究は次の４タイプに分類できます。

タイプ１： 回転体
タイプ２： 頂上が２次元である山
タイプ３： フーセンガムっぽいホイップクリーム
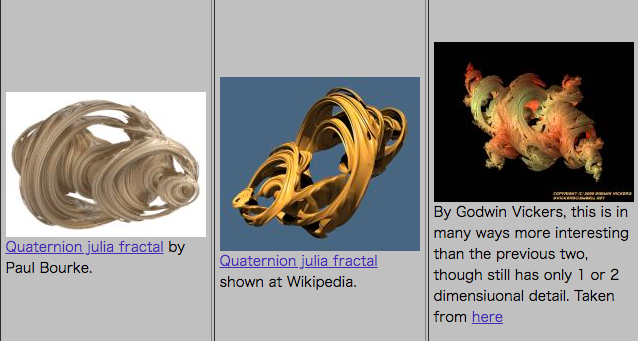
タイプ４： ジャングルジムの狂気

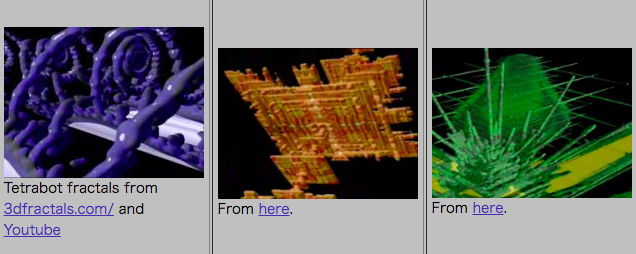本記事のコードで描画できる図形は、おそらくタイプ1:回転体です。このタイプは四元数の利用を含む複数の方法で描画できるそうです。表の１行目左端にある画像を引用します。

Jules Ruisによる３次元マンデルブロ集合

###技術的なこと
Daniel Whiteのウェブサイト内の、Further exploration of the 3D Mandelbulbに示されています。

####マンデルバルブの定義
従来のマンデルブロ集合同様、次式で定義されます。

Z_{t+1} = Z_{t}^n +c

ただし、Zとcはデカルト座標系のx, y, zを表すことができる**hypercomplex ('triplex') numbers（超複素数、多元数）**です。超複素数は複素数や四元数等の一般化です。
この超複素数のべき乗は次のように定義されます：

(x,y,z)^n = r^n \bigl( \sin(\theta n) 
 \cos(\phi n) , \sin(\theta n) 
 \sin(\phi n) , \cos(\theta n) \bigr)

ただし、

\begin{align}
r &= \sqrt{x^2 + y^2 + z^2} \\
\theta &= \mathrm{atan2}( \sqrt{x^2+y^2}, z ) \\
\phi &= \mathrm{atan2}(y,x)
\end{align}

超複素数同士の和($Z_n +c $)は複素数と同様、各部同士で加算を行います。
それ以外は従来のマンデルブロ集合と同様のアルゴリズムです。
nは3Dマンデルバルブの次数で、求めているものに最も近いのはn=8のときとされています。

マンデルバルブ(左)とマンデルブロ集合(右)の比較

マンデルバルブの見た目からマンデルブロ集合を連想しづらいかもしれませんが、比較すると似ている事がわかります。

###まだ先があるかも
先述のThe Mandelbulb: first 'true' 3D image of famous fractalの中で、Daniel Whiteはマンデルバルブが完全に本物の３Dマンデルブロ集合ではないとして、次のように述べています。

“There are still ‘whipped cream’ sections, where there isn’t detail,”
“If the real thing does exist – and I’m not saying 100 per cent that it does – one would expect even more variety than we are currently seeing.”

「まだ詳細にならない”ホイップクリーム状の”場所があるんだ。」
「もし本物が存在するなら、 ―１００％あるとは言わないけど、― 今見ているものよりもっとバラエティに富んでいるはずだよ。」

##まとめ

• マンデルブロ集合の定義をおさらいし、従来２次元画像として表現される同集合を３次元空間に拡張できるのではないかという仮説を立てた
• 四元数の定義と積を利用してマンデルブロ集合の定義式を拡張した
• 拡張した集合の、高さ方向のスライス画像を生成するスクリプトをpythonで書いた
• マンデルバルブ

これを端緒に、数学に対する理解を深めていきたい。

##マンデルバルブも描画(2019/3/31追記)
折角なのでマンデルバルブのスライスも描画しました。
スライスの移動方向は前掲のコードと同様で判定条件と座標範囲を変更しています。
突起状の部分がスライドではなく収縮して出没するので、回転体ではないことがわかります。
中身が中空になったりはしないようです。

マンデルバルブ描画のコード

#実行時間を計測するマジックコマンド。jupyter環境でのみ有効。
%%time

import numpy as np
import cv2
import math

w = 800 // 2
h = 700 // 2
depth = 200 // 2 #z軸方向。これは書き出す画像の枚数になる
img = np.ones([h, w, 1]) * 255
iteration = 1000
_N = 8 #マンデルバルブの次数

#画像のピクセルを適切なスケールに変換する
#real
re_min = -1.35
re_max = -re_min
#imagi
im_min = (re_min - re_max) * h / w / 2.0
im_max = -im_min
#quart
q_min = im_min * 1
q_max = im_max * 1
print(im_min, im_max)

#範囲を変換する関数
def _map(a,b,c,d,e): # map a from b-c to d-e
  b_c = abs(b - c)
  d_e = abs(d - e)
  prop = a / b_c
  x = prop * d_e + d
  return x

#マンデルバルブに属するか判定する
def is_in_mandelbulb(a, b, d):
  x = 0
  y = 0
  z = 0
  prev_x = x
  prev_y = y
  prev_z = z
  for i in range(iteration):
    cond = x ** 2 + y ** 2 + z ** 2    
    if cond >= 4:
      return -i
    else:
      r = math.sqrt(x ** 2 + y ** 2 + z ** 2)
      r_n = pow(r, _N)
      theta = math.atan2(math.sqrt(x ** 2 + y ** 2), z)
      phi = math.atan2(y, x)
      
      
      prev_x = x
      prev_y = y
      prev_z = z
      
      x = next_x(r_n, theta, phi, a)
      y = next_y(r_n, theta, phi, b)
      z = next_z(r_n, theta, phi, d)
  return 1

#漸化式の更新用
def next_x(r_n, theta, phi, a):  
  ret = r_n * math.sin(theta * _N) * math.cos(phi * _N) + a
  return ret

def next_y(r_n, theta, phi, b):  
  ret = r_n * math.sin(theta * _N) * math.sin(phi * _N) + b
  return ret

def next_z(r_n, theta, phi, d):
  ret = r_n * math.cos(theta * _N) + d
  return ret


font = cv2.FONT_HERSHEY_SIMPLEX
#描画開始
for z in range(depth):
  for i in range(h):
    for j in range(w):
      a = _map(j, 0, w, re_min, re_max)
      b = _map(i, 0, h, im_min, im_max)
      d = _map(z, 0, depth, q_min, q_max)
      ret = is_in_mandelbulb(a, b, d)
      if ret == 1:
        color = 0
      else:
        color = _map(-ret, 0, iteration * 0.1, 255, 0)
        
      img[i, j] = color
  
  cv2.putText(img, str(d), (w-100, h-20), font, 0.75, (150, 150, 150), 1, cv2.LINE_AA)
  name = "{0:04d}".format(z)
  cv2.imwrite("out/{}.png".format(name), img)
  

1. 数学をつくった人びと〈2〉 (ハヤカワ文庫NF―数理を愉しむシリーズ), pp299-300. ＊ハミルトン以前にはガウスによる発見(1817)があり、それ以前にも四元数に関する研究は存在したものとされている。 ↩