はじめに
この記事は明治大学総合数理 Advent Calender 2017の22日目の記事です。本Advent Calender 7回目の出演です。よろしくお願いします。
目標
Mandelbrot集合をProcessingで描こう。
Mandelbrot集合とは
Mandelbrot(マンデルブロ)集合とは綺麗な図形です。私の一番好きな図形です。こんなネクタイを持ってるくらいです。
数学関連のイベントには欠かせません。かっこいいです。
愛でているだけでは良くないので、ちゃんと数学的な定義をしておきます。
複素数$c$に対して、$$z_0 = 0, \ z_{n + 1} = z_n^2 + c$$により得られる複素数列$z_0, z_1, z_2, \cdots$を考える。Mandelbrot集合とは$$\lim_{n \to \infty}z_n < \infty$$となる$c$全体である。
要するに何回も何回も$z_{n + 1} = z_n^2 + c$をしても無限へと発散しないような行儀の良い複素数$c$を取ってこようという話です。
コンピュータで描くために
さて、Processingで実装しよう、となりますが、Processing及びJavaには複素数クラスがありません。もちろん複素数クラスを実装してもいいですが、そうじゃない方法で攻めます。
複素数は実部と虚部にわけられることを思い出して、$c = a + bi$としましょう。一言ことわりをいれておくと、$a$も$b$も実数で、$i$は虚数単位です。$i = \sqrt[]{-1}$です。また、$z_n = x_n + iy_n$としましょう。これも同様に$x_n$と$y_n$は実数です。
では、上に出てきた漸化式に代入しましょう。代入すると、
\begin{eqnarray}
x_{n + 1} + iy_{n + 1} & = & (x_{n} + iy_n)^2 + (a + bi) \\
& = & (x_n^2 - y_n^2 + a) \ + \ (2x_ny_n + b)i
\end{eqnarray}
となります。$x_{n+1}$と$y_{n+1}$も両方実数なので、実部と虚部に関する2つの漸化式ができあがります。
\begin{eqnarray}
x_0 = 0, & \quad & x_{n + 1} = x_n^2 - y_n^2 + a \\
y_0 = 0, & \quad & y_{n + 1} = 2x_ny_n + b
\end{eqnarray}
あとはこれを実装して$x_n$や$y_n$が無限へと発散しないような$a$と$b$を見つけてあげればよいだけです。
無限へと発散しないとはどういうこと
Mandelbrot集合に関する数列$z_0, z_1, \cdots$が無限へと発散するときはどういうときか、ということについて次のことがわかっています。
ある$n$について$|z_n| \ge 2$となると、その数列は無限へと発散する。
なので、$z_n$をずっと追っていって、その絶対値すなわち$\sqrt[]{x_n^2 + y_n^2}$が2以上になったら、その時点でもう考えていた$c$はMandelbrot集合の一員ではないことが確定するということです。
もっと言うと、Mandelbrot集合の点たちは全て半径2の円の中に入っていることがわかります。
描くためのアイディア
後はどうやって描くかだけです。まずはMandelbrot集合を描きたい範囲を考えましょう。ここでは実軸も虚軸も-2から2までとしましょう。一つ上の節から分かる通り、こうしておけばMandelbrot集合の全容が見られます。
次に描く範囲を格子状に分割しましょう。例えば、縦横600分割してみましょう。
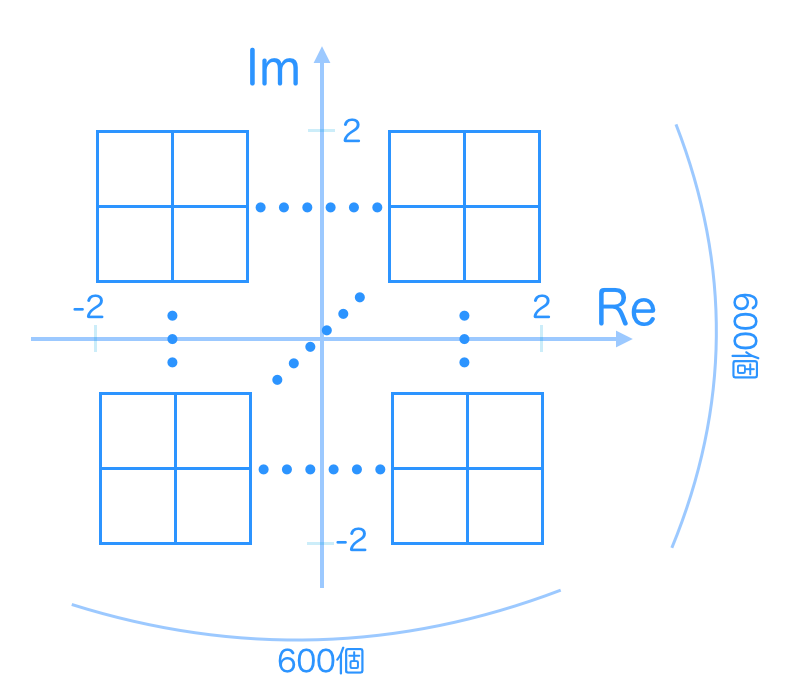
そうしたら、それぞれの格子を代表する点を選びましょう。今回はそれぞれの正方形の四つ角の内左上を代表にします。
最後に全ての格子でMandelbrot集合の漸化式を計算しましょう。この例なら600×600=360000個分の格子で計算して、発散したかどうかを記憶しておきます。予め計算回数を決めておいて、$\sqrt[]{x_n^2 + y_n^2}$がその計算回数までずっと2未満だったらその$c$はMandelbrot集合の要素です。
プログラム
きれいに見えるように色々工夫した。ちなみにProcessingは3系です。
// # of grids
int w = 800;
int h = 700;
// grid information
int[][] m = new int[h][w];
// iteration limit
int iteration = 1000;
// canvas size
float reMin = -2.0;
float reMax = 0.70;
float imMin = (reMin - reMax) * h / (float)w / 2.0;
float imMax = -imMin;
void settings() {
size(w, h);
}
void setup () {
background(255);
float a, b;
// iterate Mandelbrot!!!!
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
a = map((float)j, 0, (float)w, reMin, reMax);
b = map((float)i, 0, (float)h, imMin, imMax);
m[i][j] = isInMandelbrot(a, b);
}
}
drawMandelbrot(m);
}
// check whether c = a + bi is in Mandelbrot set
// 1 = yes, -iteration ~ -1 = diverging speed
int isInMandelbrot (float a, float b) {
float x = 0;
float y = 0;
float prevX = x;
float prevY = y;
for (int i = 0; i < iteration; i++) {
if (x * x + y * y >= 4.0) {
return -i;
}
else {
prevX = x;
prevY = y;
x = nextX(prevX, prevY, a);
y = nextY(prevX, prevY, b);
}
}
return 1;
}
// calculating x_{n + 1} and y_{n + 1}
float nextX (float x, float y, float a) {
return x * x - y * y + a;
}
float nextY (float x, float y, float b) {
return 2 * x * y + b;
}
// color the canvas
void drawMandelbrot(int[][] m) {
noStroke();
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
if (m[i][j] == 1) {
fill(0);
}
else {
fill(map(- m[i][j], 0, iteration * 0.1, 255, 0));
}
rect(j, i, 1.0, 1.0);
}
}
}
実行結果
実軸が大体(-0.9から-0.6)。Seahorse valley(タツノオトシゴの谷)といって、愛おしくてたまらない場所。

結論
Mandelbrot集合が描けた。
