Glow: Generative Flow with Invertible 1x1 Convolutions (Diederik P. Kingma, Prafulla Dhariwal)を読んだので、要約とメモ。
筆者の理解と疑問は青色でメモしている。
一言で言うと、高解像度画像を効率的に生成できるflow。対数尤度ベースのモデルとしてこれができるのは最初らしい。(arXiveへの投稿が2018.7)
大雑把に言うとチャネルの置換を1x1Convolutionに置き換えたRealNVP。
本文
概要
フロー(Flow)をベースにした生成モデル(Dinh et al., 2014)はlog尤度そのものを扱える、潜在変数の推定がしやすい、訓練時・生成時両方で並列化しやすい、といった嬉しい特性がある。本論文では可逆(invertible)な1x1convolutionを使ったシンプルな生成的Flowである、Glowを提案する。本手法により、標準的なベンチマークでlog尤度に大きな改善が見られたことを示す。最も重大なことは、普通のlog尤度の目的関数で最適化された生成モデルが、リアルな画像を合成可能で、大きい画像も扱えることである。ソースコードはhttps://github.com/openai/glow を参照。
 **図1**:本論文のモデルで合成された著名人たち。アーキテクチャと手法は3章。5章にも結果画像がある。
**図1**:本論文のモデルで合成された著名人たち。アーキテクチャと手法は3章。5章にも結果画像がある。
1. イントロ
機械学習の未解決問題として、次が挙げられる。
- データ効率:人間のように少ないデータから学習できること
- 一般化:タスクやその文脈に対するロバスト性
AIシステムは、学習データの分布とは異なる入力が来たときに全く動作しないことがある。生成モデルに対する期待は、これらの制限を次によって克服することである。
- 現実世界のモデルを学習し、エージェントが実際に世界と関わる前に、世界モデルで計画を立てられる可能性があること。
- ラベリングや教師がなくても、入力から意味のある特徴を学習できること。そのような特性はラベル付けされていない巨大データセットから学習でき、タスク特有である必要もないので、これらの特性に基づくソリューションはロバストで、データ効率が良いものとなる。
本論文では、生成モデルのsotaの改善を狙い、その結果として生まれる応用のためだけでなく、この究極のビジョンのために研究を行った。
生成モデリングは、結合分布で表される非常に高次元の入力中のすべての依存関係をモデリングするので、極めて難しい問題と考えられている。そのようなモデルはデータ中に現れるすべてのパターンを捉えうるので、正確な生成モデルの応用先は無限にある。スピーチ合成、テキスト解析、半教師あり学習、モデルベース制御など多様な用途が考えられる(4章参照)。
生成モデルの研究は近年大きな進歩を経験しているが、その多くが尤度に基づく手法**(Graves, 2013; Kingma and Welling, 2013, 2018; Dinh et al., 2014; van den Oord et al., 2016a)**とGAN(Goodfellow et al., 2014)である(4章)。尤度ベースのものは3カテゴリに分かれる
- 自己回帰モデル(Hochreiter and Schmidhuber, 1997; Graves, 2013; van den Oord et al., 2016a,b; Van Den Oord et al., 2016)。シンプルであるが、合成が並列化できない。(現在の処理が前の時刻の処理結果に依存するため計算を独立させられない)したがってデータの次元数に計算時間が依存する。画像や映像では問題となる。
- 変分オートエンコーダ(VAE)(Kingma and Welling, 2013, 2018)、データのlog尤度の下界を最適化する。訓練と合成の並列化でメリットがあるが、最適化が比較的難しい。(Kingma et al., 2016)
- Flowをベースにした生成モデル、NICE **(Dinh et al., 2014)**で最初に説明され、RealNVP **(Dinh et al., 2016)**で拡張された。次の章でこのクラスのキーアイデアを説明する。
今まで、研究コミュニティではflowベースの生成モデルはGANやVAEよりも注目を浴びてこなかった。このモデルの利点は
- 正確な潜在変数推定と対数尤度の評価が可能。VAEでは、データ点に対応する潜在変数の値を近似的に推定することしかできない。GANでは潜在変数を推定するエンコーダは存在しない。GANは潜在変数をランダムにサンプルしていた
可逆な生成モデルでは近似なしで正確に推定できる。これは正確な推定につながるし、下界ではなくデータの対数尤度そのものを最適化できる。 - 推定と合成が効率的。PixelCNN(van den Oord et al., 2016b)のような自己回帰モデルは、可逆だが、合成の処理を並列化しづらく、普通は並列ハードウェアで非効率である。GlowやRealNVPのようなflowベースモデルは推定と合成両方で効率的に並列化できる。推定と合成。合成は画像の生成として、推定ってなんのことだろう。学習のときに尤度関数を最適化するのを最尤推定の意味で推定というのだろうか?
- 潜在空間が別のタスクに有用。自己回帰モデルの隠れレイヤは未知の周辺分布を持っており、有効なデータ操作をするのが難しい。GANはエンコーダを持っておらず、データ分布上の完全な台を持たないと考えられるため、通常、データ点が潜在空間に直接表現されはしない**(Grover et al., 2018)**。完全な台を持たない=データセット内のデータをすべて表現できるとは限らない。という意味だと思う
これはデータ点間の補完や既存データ点の意味のある修正が可能な、可逆な生成モデルとVAEには当てはまらない。 - メモリ消費を大きく抑えられる。可逆なニューラルネットが勾配計算に要するメモリ量はモデルの深さに対して線形ではなく、定数である。 RevNet(Gomez et al., 2017)で説明されている。
本論文では新しい生成的flowであるGlowを提案する。その新しい要素は3章。従来のflowとの量的な比較を5章。高解像度データセットでの本モデルの質的な調査を6章で述べる。
2. 背景:Flowベースの生成モデル
$\boldsymbol{x}$を未知の分布に従う高次元ランダムベクトルとする。$\boldsymbol{x} \sim p^{*}(\boldsymbol{x})$。データをデータセットDからi.i.dに集め、パラメータ$\theta$を持つモデル$p_{\theta}(\boldsymbol{x})$を選ぶ。離散データ$\boldsymbol{x}$の場合、対数尤度目的関数は次を最小化することと等しい。
L(D) = \frac{1}{N} \sum_{i=1}^{N} - log p_\theta(\boldsymbol{x}^{(i)}) \tag{1}
$\boldsymbol{x}$が連続データの場合、
L(D) \simeq \frac{1}{N} \sum_{i=1}^{N} - log p_\theta(\boldsymbol{\tilde{x}}^{(i)})+c \tag{2}
$\boldsymbol{\tilde{x}^{(i)}}=\boldsymbol{x^{(i)}}+u$であり、$u \sim U(0,a)$、そして$c= -M \cdot log a$である。ここで$a$はデータの離散化レベルで決まり、$M$は$\boldsymbol{x}$の次元数。目的関数$(1),(2)$どちらも、natsまたはbitsにおける期待圧縮コストを表している**(Dinh et al., 2016)。最適化はミニバッチを使用したSGDで行われる(Kingma and Ba, 2015)**。
多くのFlowベースの生成モデル**(Dinh et al., 2014, 2016)**では生成プロセスは次のように定義される。
\begin{align}
\boldsymbol{z} \sim p_{\theta}(\boldsymbol{z}) \tag{3} \\
\boldsymbol{x} = g_{\theta}(\boldsymbol{z}) \tag{4}
\end{align}
$\boldsymbol{z}$は潜在変数。$p_{\theta}(\boldsymbol{z})$は(通常は)、球状多変量ガウス分布$p_{\theta}(\boldsymbol{z})= \mathcal{N}(\boldsymbol{z};0,\boldsymbol{I})$のような、計算可能な密度。データ点$\boldsymbol{x}$があり、潜在変数の推定が$\boldsymbol{z}=\boldsymbol{f_{\theta}(\boldsymbol{x})}=\boldsymbol{g_{\theta}}^{-1}(\boldsymbol{x})$となるように、関数$\boldsymbol{g_{\theta}}$は可逆とする。全単射とも呼ばれる。
簡潔にするため、$\boldsymbol{g_{\theta}}$と$\boldsymbol{f_{\theta}}$から$\theta$を省略する。
変形の系列で構成される関数$\boldsymbol{f}$($\boldsymbol{g}$も同様)に焦点を当てる。つまり$\boldsymbol{f}=\boldsymbol{f_1} \circ \boldsymbol{f_2} \circ \cdot \cdot \cdot \circ \boldsymbol{f_k}$であり、$\boldsymbol{x}$と$\boldsymbol{z}$の関係は次のように書ける
\boldsymbol{x}
\overset{f_1}{\longleftrightarrow} \boldsymbol{h_1} \overset{f_2}{\longleftrightarrow} \boldsymbol{h_2} \cdot \cdot \cdot \overset{f_k}{\longleftrightarrow} \boldsymbol{z} \tag{5}
このような可逆変形の系列は**(normalizing) flow (Rezende and Mohamed, 2015)**とも呼ばれる。$(4)$の変数変換のもとで、データ点を受け取ったモデルの確率密度関数(pdf)は次のように書ける
\begin{align}
logp_{\theta}(\boldsymbol{x})&=logp_{\theta}(\boldsymbol{z}) + log | det(\frac{d\boldsymbol{z}}{d\boldsymbol{x}})| \tag{6} \\
&= logp_{\theta}(\boldsymbol{z}) + \sum_{i=1}^{K} log | det(\frac{d\boldsymbol{h_i}}{d\boldsymbol{h_{i-1}}})| \tag{7}
\end{align}
ここの$\sum_{i=1}^{K}$は変換の数。時系列ではない。(後のほう読んでてわからなくなった)
簡単のため、$\boldsymbol{h_0} \triangleq \boldsymbol{x}$および$\boldsymbol{h_k} \triangleq \boldsymbol{z}$と定義した。スカラー値$log | det(\frac{d\boldsymbol{h_i}}{d\boldsymbol{h_{i-1}}})|$はヤコビ行列の行列式の絶対値の対数であり、log-determinantとも呼ばれる。この値は$h_{i-1}$から$h_{i}$へ進む時のlog密度の変化を表している。見た目はいかついが、特定の変換についてはこの値は驚くほど簡単になる**(Deco and Brauer, 1995; Dinh et al., 2014; Rezende and Mohamed, 2015; Kingma et al., 2016)**。基本的なアイデアは、ヤコビアン(日本語ではヤコビ行列)$\frac{d\boldsymbol{h_i}}{d\boldsymbol{h_{i-1}}}$が三角行列になるように変形を選ぶことである。この変形に関して、log-determinantは簡単になり、
log|det(\frac{d\boldsymbol{h_i}}{d\boldsymbol{h_{i-1}}})| = sum(log|diag(\frac{d\boldsymbol{h_i}}{d\boldsymbol{h_{i-1}}})|) \tag{8}
sum()はベクトルの全要素の和、log()は要素ごとの対数、diag()はヤコビ行列の対角を取る。ヤコビ行列の対角を要素ごとにlogしてその和を取る操作になる
3. 生成的Flowの提案
Dinh et al., 2014,2016で提案されたNICEとRealNVPをもとに、新しいflowを提案する。flowの計算ステップの系列から構成され、マルチスケールの構造に取り込んでいる(図2)。flowの各ステップはactnorm(3.1節)、可逆1x1convolution(3.2節)、カップリングレイヤ(3.3節)で構成される(詳細はDinh et al.,2016参照)。この構造の深さは$K$個のflowであり、レベルの数は$L$(図2参照)。
このflowはマルチスケール構造に結合される。
 **図2**: 生成的Flowの各ステップ(左図)は**actnorm**, **可逆1x1convolution**, **アフィン変換**で構成**(Dinh et al., 2014)**。このflowがマルチスケール構造(右)に結合される。3章と**表1**を参照。
**図2**: 生成的Flowの各ステップ(左図)は**actnorm**, **可逆1x1convolution**, **アフィン変換**で構成**(Dinh et al., 2014)**。このflowがマルチスケール構造(右)に結合される。3章と**表1**を参照。
3.1. Actnorm:データ依存な初期化を使用した「スケール&バイアス」レイヤー
Dinh et al. (2016)で、著者らは深いモデルの訓練で起こる問題の回避のためにbatch normalization (Ioffe and Szegedy, 2015)の使用を提案した。しかしノイズ付加されたbatch normalizationのactivationの分散はGPU(または他のprocessing unit(PU))ごとのミニバッチサイズに逆比例し、PUごとのミニバッチサイズが小さい場合には性能が落ちることが知られている。activationというのはbatch normとかレイヤを通したあとの値のことを言ってるはず
大きな画像ではメモリ制約のためにPUごとにミニバッチサイズ1で学習する。本論文ではactnorm(activation normalization)レイヤを提案する。これはbatch normalizationに似ており、チャネルごとのバイアスとスケールのパラメータを使用してactivationのアフィン変換を行う。これらのパラメータは最初のミニバッチが来たときに、actnormの後のactivationがチャネルごとに平均0、分散1になるように初期化される。これはデータ依存初期化の一種である**(Salimans and Kingma, 2016)**。初期化後、スケールとバイアスのパラメータはデータと独立な通常の訓練可能パラメータとして扱う。
3.2. 可逆 1x1 convolution
(Dinh et al., 2014, 2016)はチャネルの順番を逆にする置換と等価な操作を含むflowを提案した。本論文は、この固定の置換を学習された可逆1x1convolutionに置き換えることを提案する。このconvolutionは重み行列がランダムな回転行列で初期化される。入力と出力のチャネル数が等しい1x1convolutionというのは、置換操作の一般化になる。
$c \times c$の重み行列$\boldsymbol{W}$を使った、$h \times w \times c$のテンソル$\boldsymbol{h}$の、可逆1x1convolutionのlog-determinantは簡単に計算でき、
log \left| det(\frac{d conv2D(\boldsymbol{h};\boldsymbol{W})}{d\boldsymbol{h}}) \right| = h \cdot w \cdot log \left|det(\boldsymbol{W})\right| \tag{9}
右辺では左辺の入力テンソルhが消えてる。この操作は(7)式の右辺第2項のためにやってるんだと思うが、これって入力関係なく求まるのか
$det(\boldsymbol{W})$を計算・微分するコストは$\mathcal{O}(c^3)$であり、$conv2D(\boldsymbol{h};\boldsymbol{W})$のコスト$\mathcal{O}(h \cdot w \cdot c^2)$と互角であることが多い。重み$\boldsymbol{W}$はランダムな回転行列で初期化したので、log-determinantは0であり、SGDの1ステップ以降は0から離れ始める。回転行列の行列式は1であるため、logを取ると0になる。
LU分解
$det(\boldsymbol{W})$を計算するコストは、$\boldsymbol{W}$をそのLU分解で直接パラメータ表示(媒介変数表示)することで、$\mathcal{O}(c^3)$から$\mathcal{O}(c)$に減らせる。
$\boldsymbol{W}=\boldsymbol{PL}(\boldsymbol{U}+diag(\boldsymbol{s})) \tag{10}$
$\boldsymbol{P}$は置換行列、$\boldsymbol{L}$は対角に1がある下三角行列、$\boldsymbol{U}$は対角に0がある上三角行列、$\boldsymbol{s}$はベクトル。置換行列は各行、各列に一つだけ1があり、それ以外0の正方行列。sは何のベクトル?
log-determinantは簡単に次のように書ける。
log|det(\boldsymbol{W})| =sum(log|\boldsymbol{s}|) \tag{11}
実験の際に実際の経過時間で計測はしなかったが、$c$が大きい時、コストの差は非常に大きくなる。
このパラメータ表示では、最初にランダムな回転行列$\boldsymbol{W}$をサンプルすることでパラメータを初期化し、その後対応する$\boldsymbol{P}$(これは固定する)の値を計算、そして$\boldsymbol{L}$,$\boldsymbol{U}$,$\boldsymbol{s}$を計算する(これらは最適化する)。
3.3. アフィンカップリングレイヤー
**(Dinh et al., 2014,2016)**で導入された強力な可逆変形。通常方向も逆方向も、log-determinantも計算効率がよい。表1参照。加法的カップリングレイヤは$s=1$の特殊なケースで、log-determinantが0になる。
表1: 提案したflowの主要な要素について、関数、逆関数、log-determinantを示した。$\boldsymbol{x}$はレイヤの入力、$\boldsymbol{y}$は出力。$\boldsymbol{x},\boldsymbol{y}$とも、[$h \times w \times c$]のテンソル。$\boldsymbol{x},\boldsymbol{y}$内の空間的な位置を$(i,j)$で表す。関数NN()は**ResNets (He et al., 2016)やRealNVP (Dinh et al., 2016)**に見られる浅いCNNのような非線形写像。

ゼロ初期化
各アフィンカップリングレイヤが最初は恒等写像になるように、各NN()の最後の畳み込みをゼロで初期化する。この操作は非常に深いネットワークを訓練しやすくする。畳み込みがゼロだと、NN()の出力は(logs, t)でなので(1,0)。その後$s=exp(logs)$, $y_a=s\odot x_a +t$という操作に代入すれば、$y_a=x_a$になり、これが恒等写像になる。表1参照。
分割と結合
**(Dinh et al., 2014)にあるように、$split()$関数は入力テンソル$\boldsymbol{h}$をチャネル軸で2分割する。$concat()$はその逆。(Dinh et al., 2016)**では別のsplitが導入されており、チェッカーボードパターンを使って空間軸で分割する。本論文ではチャネル軸のみ使用する。
置換
上で説明した各ステップの前に、何らかの変数の置換が必要である。これはflowを十分なステップ実行した後、各次元が他のすべての次元に影響することを保証するためである。各次元が他のすべての次元に〜というのは、チャネル方向でsplit()されているから、置換なしだと特定チャネルだけ特定操作に偏る。
**(Dinh et al., 2014, 2016)**で採用されている置換は、加法的カップリングレイヤの前に、チャネル(特徴)の順番を逆にすることと等価である。代わりに、(固定の)ランダム置換を行う方法がある。本論文の可逆1x1convolutionはそのような置換の一般化である。実験では、これら3つを比較した。
4. 関連研究
**(Dinh et al., 2014)(NICE)と(Dinh et al.,2016)(RealNVP)**で提案されたflowとアイデアに基づいている。
- **(Papamakarioset al., 2017) (MAF)**は、**IAF(Kingma et al., 2016)**に基づいた生成的flowを提案しているが、これは並列化不可能であり、効率的でないので比較しなかった。
- 自己回帰モデル**(Hochreiter and Schmidhuber, 1997; Graves, 2013; van den Oord et al., 2016a,b; Van Den Oord et al., 2016)は同様に並列化できない。高次元データの生成時間はたいてい複数桁も長くなる(Kingma et al., 2016; Oord et al., 2017)**。本論文の最大のモデルを使えば256 × 256の画像をサンプルするのにわずか1秒以下しかかからない(batch size=1で1080Ti1台の場合130ms, K80なら550ms)。
- GAN (Goodfellow et al., 2014)は対数尤度モデルと対照的に、大きくリアルな画像を生成できることで知られている(Karras et al., 2017)。デメリットは潜在空間エンコーダがないこと、データに対する完全な台がないこと**(Grover et al.,2018)**、最適化が難しい、過学習と汎化を評価するのが難しい。
5. 定量的実験
**RealNVP (Dinh et al.,2016)**との比較から始める。次に標準的なデータセットでの対数尤度を既存の生成モデルと比較する。実験では、NN()は3つの畳込み層を持つとし、2つの隠れ層は512チャネルあり、ReLUを持つ。最初と最後の畳み込みは3x3、真ん中は1x1。これは真ん中の畳込み層の入力と出力は、前後の層でのそれらよりチャネル数が多いため。
可逆1x1convolutionのご利益
3章で説明したアーキテクチャを使い、チャネル変数の置換のバリエーションを3つ考える。RealNVPで説明されている「逆にする操作」、固定ランダム置換、そして本論文の可逆1x1convolutionである。アフィンカップリングのモデルと、加法的カップリングのモデルの比較だけ行う。先述の通り、全てのモデルは各レイヤのactivationを正規化するデータ依存な初期化を行う。モデルは全て$K=32, L=3$で訓練した。1x1convolutionのモデルは他より0.2%だけパラメータ数が多かったが、無視できる範囲である。
CIFAR-10(Krizhevsky,2009)で、負の対数尤度(bits per dimension)の平均を比較した。3つのランダムシードを平均して、すべての訓練の条件を一定にした。結果は図3。**加法的、アフィンどちらの場合も、他の置換方法よりも可逆1x1convの負の対数尤度は低く、収束が早いことがわかる。**また、アフィンの場合は加法的モデルよりも収束が早い。可逆1x1convで増えた計算時間はおよそ7%に過ぎなかったので、この操作も計算効率が良いと言える。
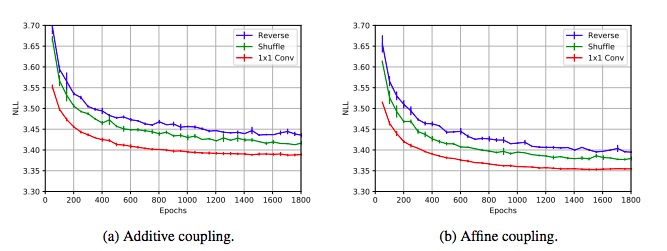
図3:加法的(左図)およびアフィン(右図)カップリングレイヤにおける3種類の置換の比較。異なるランダムシードで実験を3回行い、その平均と標準偏差をプロットした。
標準ベンチマークでのRealNVPとの比較
置換とは別に、RealNVPのアーキテクチャは空間的カップリングレイヤという別の特徴がある。本論文のアーキテクチャがRealNVPとあらゆる点で互角であることを確認するために、様々な自然な画像のデータセットで比較を行った。特にCIFAR-10, ImageNet(Russakovsky et al., 2015), LSUN (Yu et al., 2015)。(Dinh et al., 2016)に従い、Imagenetは32x32と64x64のダウンサンプル版(Oord et al., 2016)を使用。LSUNは96x96にダウンサンプルし、64x64のランダムサンプルを使用。定性的実験で使用した256x256のCelebA HQで訓練したモデルではbits/dimensionを使用する。bits/dimensionは対数尤度から変換で導出できるっぽい。定義は見つけられてない。PixelCNNとか読んだら書いてあるかも
表2からわかるように、本モデルは全てのデータセットで大幅な改善を達成している。
表2:bits/dimensionでRealNVPと比較した本モデルの性能

6.定性的実験
高解像度データセットでの質的な側面を調査する。 CelebAデータセットの画像から作成された30,000枚の高解像度画像からなる**CelebA-HQ dataset (Karras et al., 2017)**を使用し、先述したアーキテクチャと同じ、ただし画像の解像度が$256^2$、$K=32, L=6$として訓練する。見た目を改善するために、少し色の忠実度を下げて、5bit画像で訓練する。一般的な画像は8bitが3チャネル。8bitなら256段階だが、5bitだと32段階の階調しか表現できない。
この実験で、高解像度にもスケールするか、リアルな画像を作れるか、意味のある潜在空間を構築できるか、を検証したい。メモリ制約のため、この解像度ではPU(プロセッシングユニット)ごとにミニバッチサイズ1を使用し、gradient checkpointing (Salimans and
Bulatov, 2017)を使った。20%計算コストを増やすだけで10倍大きいモデルをメモリに載せられるとのこと。ちら見しただけだが、保持できる値の最大数みたいのを決めておいて、それを超えそうになったら要らない値を破棄していくみたいな手法。こちらに著者による解説がある。
将来的には、本モデルの可逆性を利用してモデルの深さと関係なく一定のメモリ消費、ということになるかもしれない(Gomez et al., 2017)
**(Parmar et al., 2018)**の尤度ベース生成モデルの先行研究と同様、reduced-temperature modelからサンプルすると品質が上がることがある。温度$T$でサンプルした時、分布$p_{\theta,T}(\boldsymbol{x}) \propto (p_{\theta}(\boldsymbol{x}) )^{T^2}$からサンプルすることになる。加法的カップリングレイヤの場合、単に$p_{\theta}(\boldsymbol{z})$の標準偏差にTをかけることでできる。
合成と補完
図4はモデルから得られたランダムなサンプル。画像は自己回帰ではない尤度ベースモデルにしては極めて高品質である。補完の性能をみるために、実写画像のペアを用意し、エンコーダーでエンコードし、画像を得るために2つの画像に対応する潜在変数の間を線形補間した。
結果は図5であるが、ジェネレータ分布の画像多様体は極めてなめらかであり、ほとんどすべての中間サンプルは本物の顔に見える。意味のある潜在空間を構築できた。

図4:モデルから得たランダムなサンプル。温度は0.7。

図5:潜在空間での2枚の実写画像の線形補間。
意味操作
画像の属性を修正すること考える。そのために、CelebAデータセットのラベルを使用する。各画像は、笑い、ブロンドヘア、若い、などの属性があるかないかを示す2値のラベルがついている。各属性について30,000個の2値ラベルがあることになる。ある属性を持つ画像については潜在変数の平均$\boldsymbol{z_{pos}}$を、持たないものは$\boldsymbol{z_{neg}}$を計算し、操作の方向として差$(\boldsymbol{z_{pos}}-\boldsymbol{z_{neg}})$を使用する。これは比較的小さい介入であり、モデルが訓練された後に行う(訓練中にラベルは使用しない)。これにより、多様な属性に対して行うことが簡単になる。結果は図6。

図6:属性の操作。各行は画像の潜在コード(潜在空間に写像された画像のベクトル)を特定の属性に対応するベクトルに沿って補完することで作成した。中間の画像がオリジナル。
温度とモデル深さの効果
図8は温度によってサンプルの品質と多様性がどのように変わるかを示した。最も高い温度ではノイズっぽい画像ができ、データ分布のエントロピーを過大に推定したためと考えられる。したがって、多様性と品質のスイートスポットとして温度0.7を選んだ。図9はモデルの深度が、長期の依存関係を学習する能力に対してどのように影響するかを示す。

図8:温度を変更した場合の影響。左から右に温度0, 0.25, 0.6, 0.7, 0.8, 0.9, 1.0のときの結果。
 **図9**:浅いモデル(左)と深いモデル(右)から得たサンプル。浅いモデルは$L=4$, 深いモデルは$L=6$
**図9**:浅いモデル(左)と深いモデル(右)から得たサンプル。浅いモデルは$L=4$, 深いモデルは$L=6$
7.結論
新しいタイプのflowであるGlowを提案し、標準モデリングベンチマークでの対数尤度に関して性能の改善を示した。さらに、高解像度の顔画像で訓練した時、本モデルはリアルな画像を生成できることを示した。本モデルは、著者らが知る限り、高解像度の自然な画像を効率的に生成できる最初の対数尤度ベースのモデルである。
本記事のまとめ
- flowをベースにした生成モデルの提案。GANやVAEとは異なる。
- 高解像度画像を効率的に生成できる。
展望
- DO DEEP GENERATIVE MODELS KNOW WHAT THEY DON’T KNOW? (Nalisnick et.al.)を読んだ時にGlowがわからなかったので本記事を書いたが、もっと基本的な仕組みはNICE(Dinh et al., 2014)とRealNVP (Dinh et al., 2016)を読む必要がありそう。