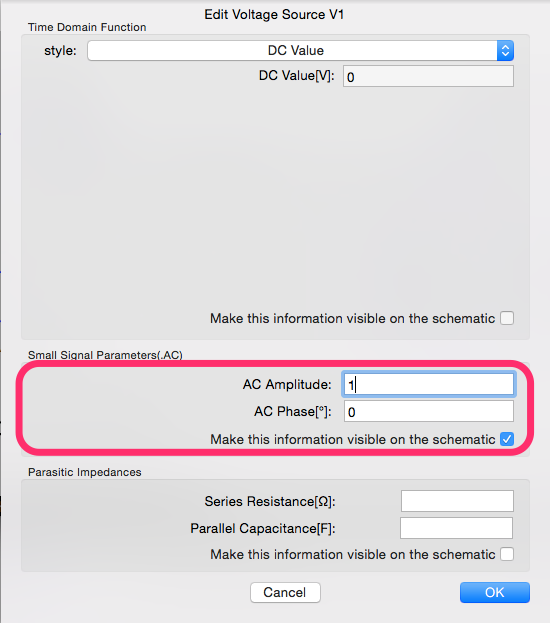
概要
シミュレーションツール LTspice で「ウィーンブリッジ発振回路」の挙動を調べる。
はじめに
LTspiceの練習のために、オペアンプを使ってサイン波を発生させて、その挙動を確認する。
オペアンプでサイン波といえば「ウィーンブリッジ発振回路」だ。
なお、LTspice については、下記も参考にしてください。
- 回路シミュレーション LTspice の使い方(2) 部品の追加
http://qiita.com/exabugs/items/5bfb3a575ce05bb6cbde - ESP8266 (ESP-WROOM-02) 回路シミュレーション・ツール LTspice (無料) の使い方 まとめ
http://qiita.com/exabugs/items/59536e2a52aa460087d5
ウィーンブリッジ発振回路
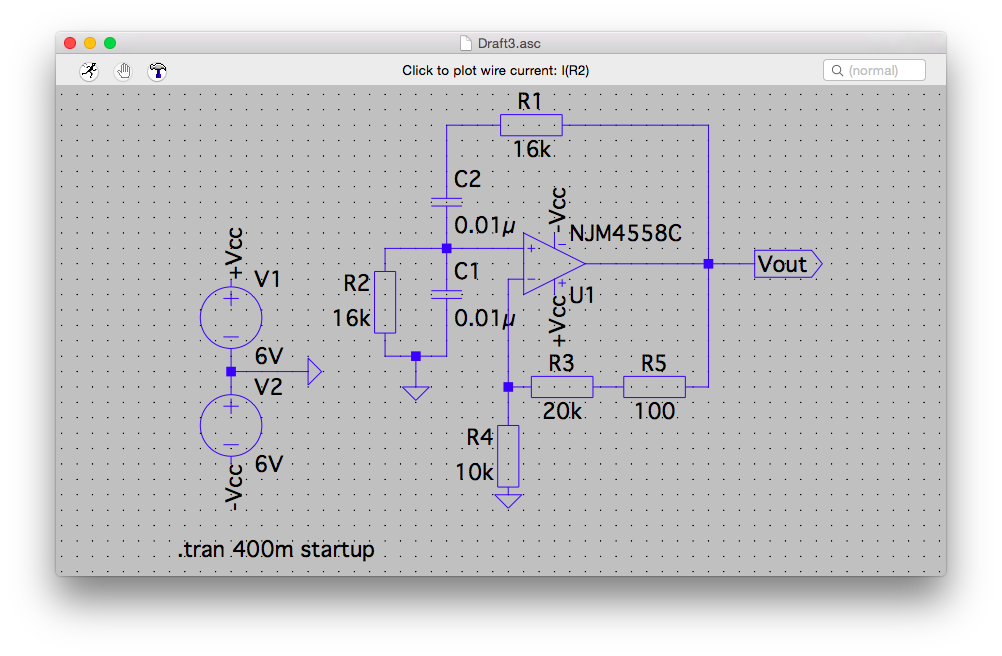
計算通り、ピッタリ増幅率が 3 (R4:10kΩ, R3:20kΩ)の場合だと、LTspiceでは発振しなかった。
そのため、R5(100Ω) を足して、増幅率を 3 より少しだけ大きくしている。
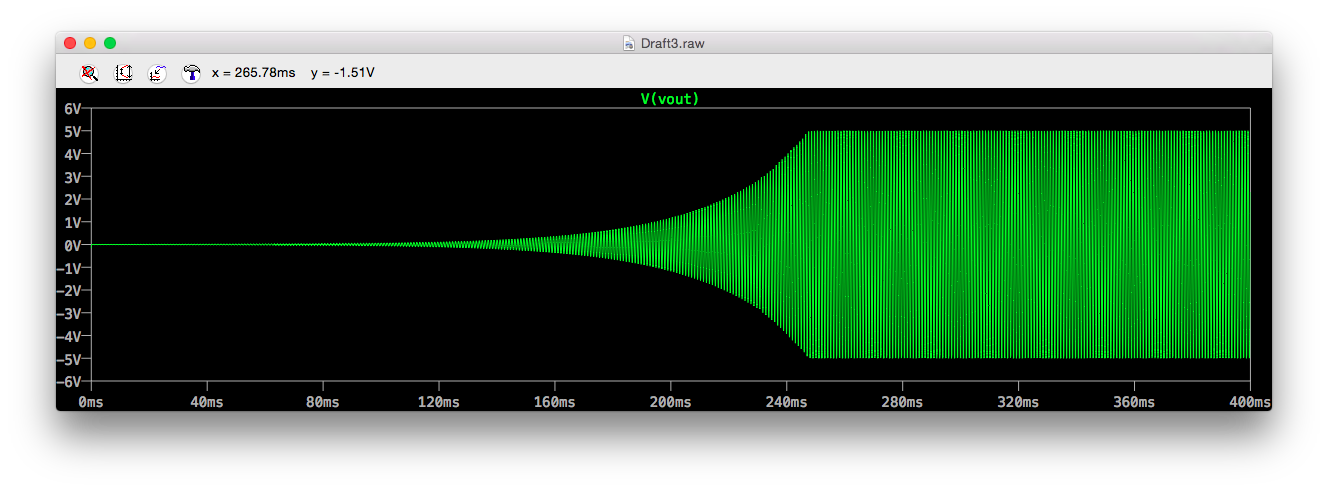
シミュレーション結果
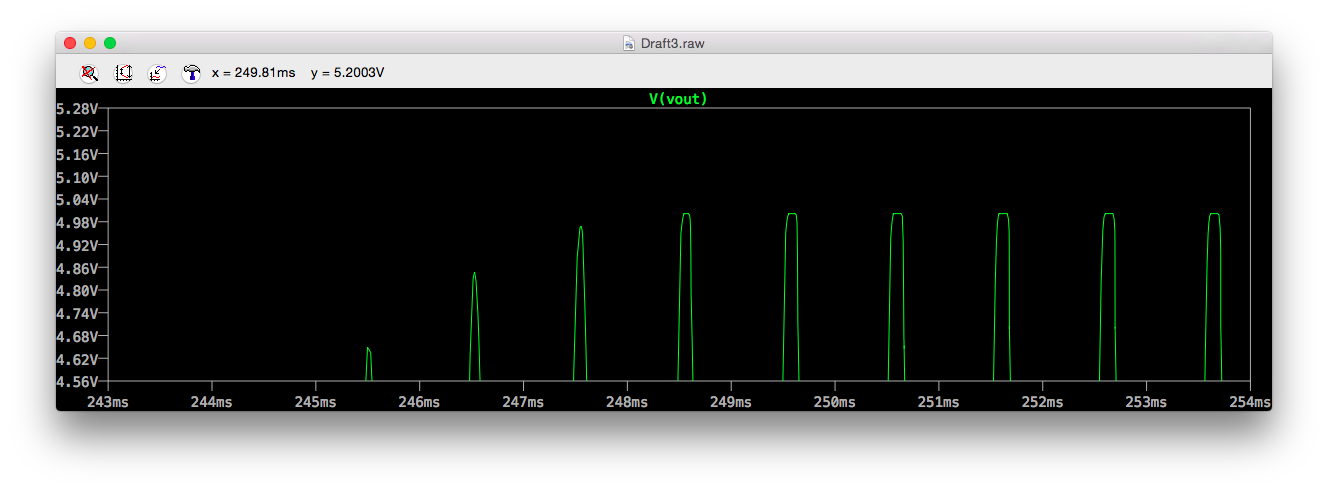
拡大図
頂点で波形が歪んでいないか確認。しかし、微妙に潰れている。。
(結果グラフ上で、拡大したい部分をマウスでドラッグすると拡大される)
ウィーンブリッジ発振回路は、全く歪まずには発振しないのではないかと思うが、どうなのだろう。
以下で「ウィーンブリッジ発振回路」を詳細に見ていく。
「ウィーンブリッジ発振回路」は、以下二つの部分から構成されている。
- 非反転増幅回路
- バンドパス・フィルター回路
つまり、特定周波数(ここでは 1KHz)だけ1/3、他は1/3以下にフィルタして、その後、増幅回路で3倍する、ということ。
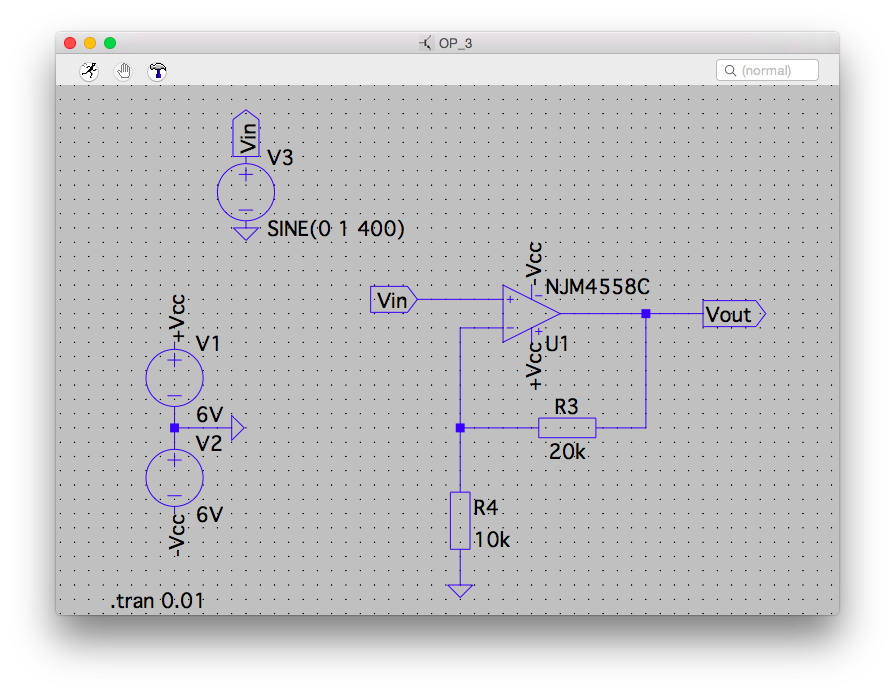
非反転増幅回路
ウィーンブリッジ回路の負帰還部分は、(全体として)非反転増幅回路を形成している。
増幅度 = (R3 + R4) / R4 = 3
検証回路
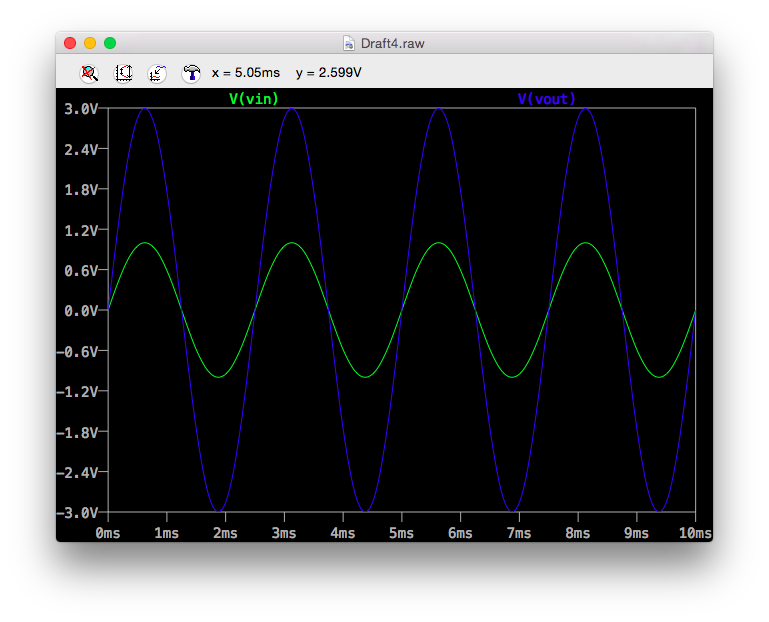
シミュレーション結果
確かに、3倍 になっている。
バンドパス・フィルター
ウィーンブリッジ回路の正帰還部分は、以下のフィルタを組み合わせた、バンドパス・フィルターを形成している。
- R1,C1 で構成されるローパス・フィルター
- C2,R2 で構成されるハイパス・フィルター
どちらも、遮断周波数（カットオフ周波数） は 994.718394324[Hz]
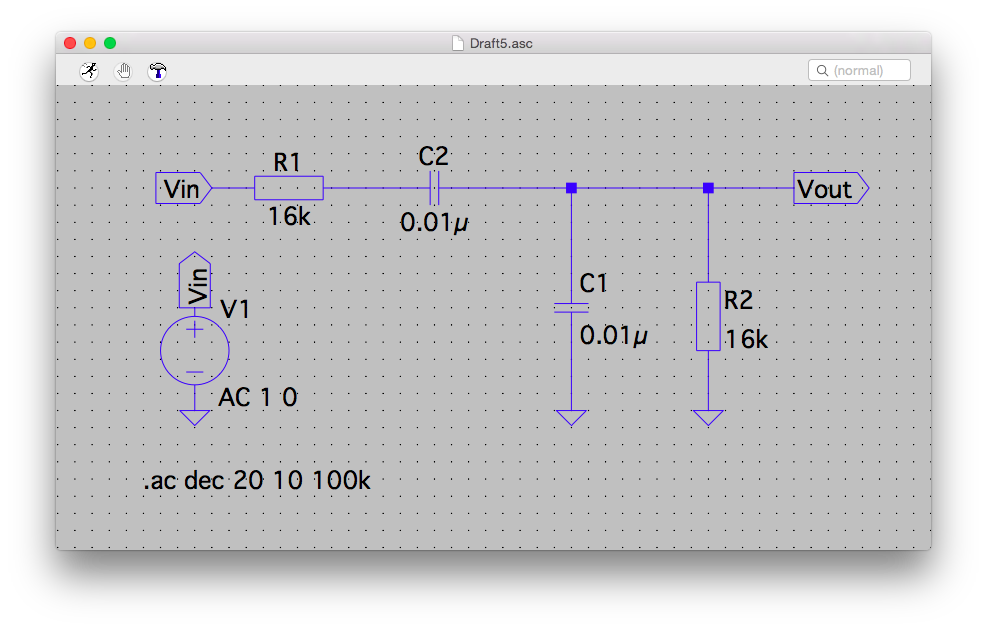
このバンドパス・フィルターの周波数特性を検証してみる。
検証回路
周波数特性をみるためには、入力信号を以下のように設定する。
また、「SPICE directive」を以下のように設定する。
上記の各値は以下の意味を持つ
| キー | 値 |
|---|---|
| Type of Sweep | Decade |
| Number of points pr decade | 20 |
| Start Frequency | 10 |
| Stop Frequency | 100k |
シミュレーション結果
1KHz付近の拡大図
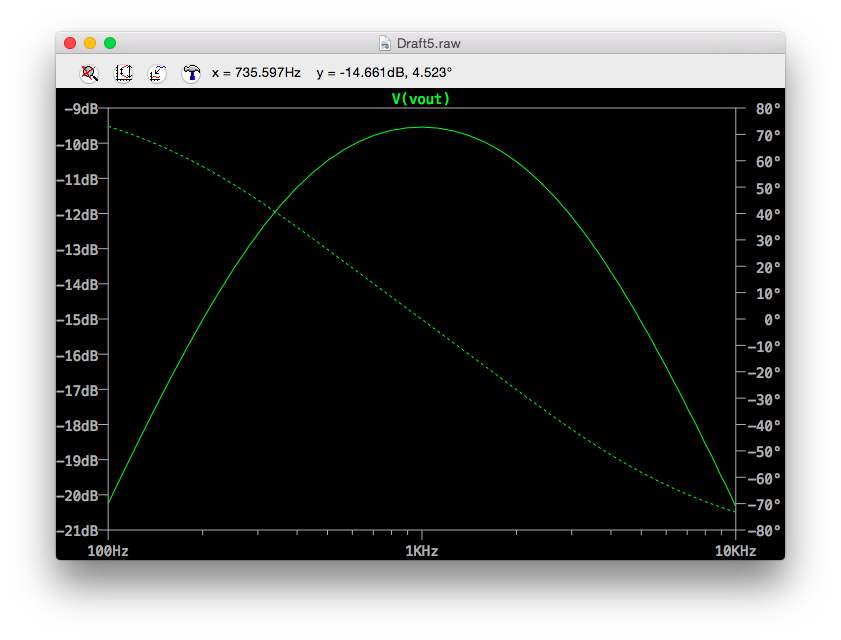
1KHz を中心に、-9dB (0.355倍) 〜 -10dB (0.316倍) 、つまり、約 1/3 倍 になっていることがわかる。
まとめ
- やっと、LTspice にも慣れてきた。
- 今後、実際の回路を作った時に、机上の計算との誤差が、気になってくる。