はじめに
2019年11月に統計検定2級を受験した後、準1級も目指してみたいと考えて学習をぼちぼち始めました。
聞くところによると準1級を取るには多変量解析を押さえておく必要があるらしい。
ということで、参考書を読んで多変量解析を学習していくのですが、理解を深めるにはやはり自分で手を動かすのが一番と考え、Pythonを使っていろんな解析手法を試してみることにします。
とはいえ、2級の勉強でなんとなく流していた、統計処理ソフト (R) の解析結果を読み取る問題ともちょっとだけ絡んできますので、タイトルは【統計検定2級・準1級】としました。
重回帰分析の回帰係数の自由度が「独立変数の数+1」だけ減るとか、「有意水準xx%で係数は0でない」といった出題がされていますが、その辺りの話は今回ご紹介する内容と関係してきます。
なお、ここでは統計ライブラリの類は使わず、numpyやpandasといったライブラリのみを使っていきます(ブラックボックスで使っていては理解の助けにならないので…)。
参考書
長谷川勝也『ゼロからはじめてよくわかる多変量解析』技術評論社 (2004) Chapter 2
題材
今回はJR東日本の「路線別ご利用状況」のデータを加工して利用させていただきます。
PDFファイルにある路線名と営業キロ、平均通過人員(2018年度)、旅客運輸収入(2018年度)のデータを整形して、以下のようなカンマ区切りデータを作成しました。
(データが不完全な「大船渡線」「気仙沼線」「山田線」は除外しています)
線名,営業キロ,平均通過人員,旅客運輸収入
山手線,20.6,1134963,111014
埼京線,5.5,752645,15032
東海道本線,169.2,367765,238493
横浜線,42.6,231706,38214
総武本線,145.4,207099,117700
京葉線,54.3,181483,38201
根岸線,22.1,177099,16618
南武線,45,163148,29946
中央本線,247.8,160328,170577
高崎線,74.7,116646,34095
武蔵野線,105.5,114847,43177
東北本線,572,84567,183688
常磐線,351,71035,100757
青梅線,37.2,63151,8989
横須賀線,23.9,62379,6107
川越線,30.6,56191,6629
外房線,93.3,34851,12038
相模線,33.3,29643,4372
五日市線,11.1,24712,1025
仙石線,49,20497,4466
内房線,119.4,20483,8544
伊東線,16.9,16907,1849
白新線,27.3,15978,1686
成田線,119.1,15183,8901
鶴見線,9.7,14133,569
篠ノ井線,66.7,12465,4717
両毛線,84.4,11346,3176
八高線,92,9338,3612
信越本線,175.3,9233,6260
仙山線,58,9046,2176
東金線,13.8,8075,373
田沢湖線,75.6,7023,4421
水戸線,50.2,7011,1255
越後線,83.8,6021,1862
日光線,40.5,5806,863
上越線,164.4,5389,3464
奥羽本線,484.5,4983,14111
左沢線,24.3,3342,244
大糸線,70.1,3140,937
弥彦線,17.4,2338,150
吾妻線,55.3,2327,615
羽越本線,271.7,2194,2731
男鹿線,26.4,1877,146
磐越西線,175.6,1745,1198
水郡線,147,1666,760
烏山線,20.4,1457,83
磐越東線,85.6,1385,371
石巻線,44.7,1255,190
鹿島線,17.4,1221,87
小海線,78.9,1194,420
久留里線,32.2,1094,96
陸羽東線,94.1,906,296
八戸線,64.9,883,269
釜石線,90.2,764,308
五能線,147.2,631,352
飯山線,96.7,598,199
大湊線,58.4,578,168
津軽線,55.8,464,112
花輪線,106.9,382,124
米坂線,90.7,379,105
陸羽西線,43,345,67
北上線,61.1,311,70
只見線,135.2,280,140
このファイルを、文字コードをUTF-8として jreast2018.csv という名前で保存しておきます。
実習
以下、Python 3.6.8で動作確認しています。
データ入力
まずはデータの取り込みをしなければいけません。
pandasを使ってCSV形式のデータを取り込みます。
import numpy as np
import pandas as pd
df = pd.read_csv("jreast2018.csv")
print(df) # 取り込んだデータの内容を確認
線名 営業キロ 平均通過人員 旅客運輸収入
0 山手線 20.6 1134963 111014
1 埼京線 5.5 752645 15032
2 東海道本線 169.2 367765 238493
3 横浜線 42.6 231706 38214
4 総武本線 145.4 207099 117700
.. ... ... ... ...
58 花輪線 106.9 382 124
59 米坂線 90.7 379 105
60 陸羽西線 43.0 345 67
61 北上線 61.1 311 70
62 只見線 135.2 280 140
回帰直線の係数を求める (2-1節)
まずは、独立変数(説明変数)$x$を「平均通過人員」、従属変数(目的変数)$y$を「旅客運輸収入」として、両者の関係をよく表す直線 $y = ax+b$ を引くことを考えます。
ある直線を引いたとき、各データ点の残差(従属変数の観測値(実現値)と理論値(予測値)との差)の二乗和を最小とするような直線を考えます。いわゆる「最小二乗法」ですね。
各データ点 $(x_1, y_1), ..., (x_n, y_n)$ について、従属変数の観測値を$y_i$、理論値を $\hat{y}_i = ax_i + b$ とすると、残差の二乗和 $L$ は
\begin{align}
L &= \sum_{i=1}^n (y_i - \hat{y}_i)^2 \\
&= \sum_{i=1}^n (y_i - ax_i - b)^2
\end{align}
となります。$L$が最小値を取るとき、$a, b$ についてそれぞれ偏微分係数は0になりますので
\begin{align}
\frac{\partial L}{\partial a} &= \sum_{i=1}^n 2(y_i - ax_i - b)(-x_i) = 0 \\
\frac{\partial L}{\partial b} &= \sum_{i=1}^n 2(y_i - ax_i - b)(-1) = 0 \\
\end{align}
これを$a, b$について整理すると
\begin{align}
\left(\sum_{i=1}^n x_i^2\right) a + \left( \sum_{i=1}^n x_i \right) b &= \sum_{i=1}^n x_i y_i \\
\left( \sum_{i=1}^n x_i \right) a + nb &= \sum_{i=1}^n y_i \\
\end{align}
$a, b$に関する連立方程式として解くと
\begin{align}
a &= \frac{n\sum_{i=1}^n x_i y_i - \sum_{i=1}^n x_i \sum_{i=1}^n y_i}{n \sum_{i=1}^n x_i^2 - \left( \sum_{i=1}^n x_i \right)^2} \\
b &= \frac{ \sum_{i=1}^n x_i^2 \sum_{i=1}^n y_i - \sum_{i=1}^n x_i \sum_{i=1}^n x_i y_i}{n \sum_{i=1}^n x_i^2 - \left( \sum_{i=1}^n x_i \right)^2} \\
\end{align}
が得られます。
この$a, b$を手計算するのは(たとえ電卓を使ったとしても)辛いですが、プログラムを使えば簡単に計算できます。
n = len(df)
X = df["平均通過人員"]
y = df["旅客運輸収入"]
a = (n * (x*y).sum() - x.sum() * y.sum()) / (n * (x**2).sum() - x.sum() ** 2)
b = ((x**2).sum() * y.sum() - x.sum() * (x*y).sum()) / (n * (x**2).sum() - x.sum() ** 2)
print(a) # Output: 0.12665116273608049
print(b) # Output: 11411.585376160469
ここから、平均通過人員が1人増えるごとに、年間旅客運輸収入が約0.127百万円(=12万7千円)増える傾向にあることがわかります。
グラフも描いてみましょう。
import matplotlib as mpl
mpl.use('Agg')
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
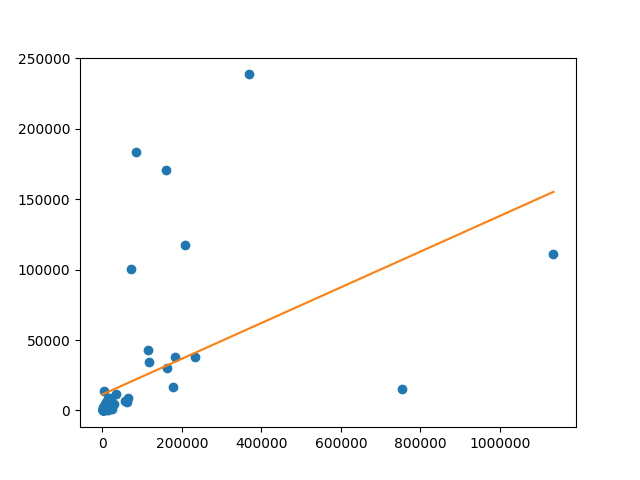
ax.scatter(x, y, color="tab:blue")
ax.plot(x, a*x + b, color="tab:orange")
fig.savefig("output.png")
うーん、あまりうまく分析できている感じがしませんね。グラフを見る限りとても直線状にはなっていないようなデータです。
右下の方にある、x軸の値が75万くらいの点は「埼京線」です。元のデータをよく見ると、平均通過人員は多いのですが、営業キロが5.5kmと短い1ために、旅客運輸収入が少ないのですね。
そういえば「平均通過人員」って何でしたっけ。(「路線別ご利用状況」より)
○ 「平均通過人員」は、ご利用されるお客さまの1日1kmあたりの人数を表し、当社が国土交通省に毎年報告する「鉄道事業実績報告書」に基づき、以下の計算により算出しています。
【平均通過人員】=【各路線の年度内の旅客輸送人キロ*A】÷【当該路線の年度内営業キロ】÷【年度内営業日数】
実際に収入に結びつくのは「旅客輸送人キロ」(利用者数×距離)なので、独立変数としては「平均通過人員×営業キロ×営業日数」(1年間を通した延べ利用距離)を使うのがより適切と考えられます。2018年度は365日間あるので、営業日数を365として計算してみましょう。
x = df["平均通過人員"] * df["営業キロ"] * 365
y = df["旅客運輸収入"]
n = len(df)
a = (n * (x*y).sum() - x.sum() * y.sum()) / (n * (x**2).sum() - x.sum() ** 2)
b = ((x**2).sum() * y.sum() - x.sum() * (x*y).sum()) / (n * (x**2).sum() - x.sum() ** 2)
print(a) # Output: 1.082862145743171e-05
print(b) # Output: 331.32038547946183
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
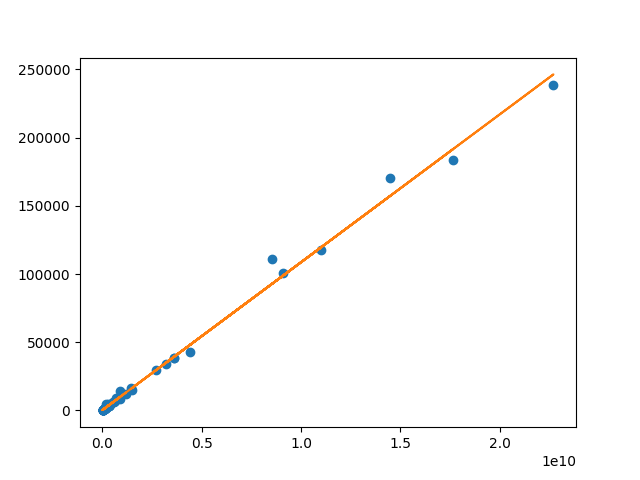
ax.scatter(x, y, color="tab:blue")
ax.plot(x, a*x + b, color="tab:orange")
fig.savefig("output.png")
いい感じですね。年間旅客輸送人キロを$x$、年間旅客運輸収入(百万円)を$y$とすると、$y$の理論値$\hat{y}$はおよそ以下で求められることになります。
\hat{y} = (1.083 \times 10^{-5}) x + 331.3
鉄道が1km利用されるたびに、収入が約10.83円増えるという計算になります。
JR(本州3社)の普通運賃の対キロ賃率(1km当たりの運賃)は16.20円(幹線内相互発着、300km以下の場合。税抜)で計算されるのですが2、定期券を買えば運賃は割引されますので、1kmの利用で得られる収入は16.20円より少なくなるでしょう。さらに、10km以下の短距離や300kmを超える長距離、利用者の少ない地方交通線など、実際には様々な運賃計算パターンがあり、データはきれいに直線に乗るものではありません。
決定係数を求める (2-2節)
さて、この回帰式がどれほどうまく当てはまっているかを確認するために、決定係数$R^2$を求めてみましょう。
観測値$y_i$が持っている変動として
- 全変動:全データ点の平均からの変動(偏差の二乗和)
- 回帰変動:回帰式で求められる理論値からの変動、つまり回帰式で説明される変動(偏差の二乗和)
- 残差変動:回帰式で説明されない変動(偏差の二乗和)
を全データ点にわたる総和で考えると、(全変動)=(回帰変動)+(残差変動)が成り立ちます。ここで、全変動に占める回帰変動の割合が決定係数$R^2$です。決定係数が大きい(1に近い)ほど、回帰式がデータによく当てはまっていると考えられます。
TSS = ((y - y.mean()) ** 2).sum() # 全変動
ESS = ((a*x+b - y.mean()) ** 2).sum() # 回帰変動
RSS = ((y - a*x+b) ** 2).sum() # 残差変動
R_2 = ESS / TSS # 決定係数
print(TSS) # 139066190955.65082
print(ESS) # 138362318781.54144
print(RSS) # 731535019.9636117
print(R_2) # 0.9949385816259694
決定係数は0.995と、よく当てはまっている様子がわかります。元々の運賃計算が距離に比例する方法をベースにしているため、そこまで変な話でもないと思います。
(全変動)=(回帰変動)+(残差変動)となるはずですが、桁数の異なるデータをごちゃごちゃに扱ったため、情報落ちによる誤差が生じているようです。
なお、ここで求めた決定係数は、実は独立変数・従属変数の相関係数の2乗に等しくなります。試しに(標本)相関係数を求めて確認してみましょう。
cov_xy = ((x - x.mean()) * (y - y.mean())).sum() / (n - 1) # 標本共分散
var_x = ((x - x.mean()) ** 2).sum() / (n - 1) # 独立変数の標本分散
var_y = ((y - y.mean()) ** 2).sum() / (n - 1) # 従属変数の標本分散
corr = cov_xy / np.sqrt(var_x * var_y) # 相関係数
print(corr ** 2) # 0.994938581625969
確かに、先ほど求めた決定係数に一致しているようです(計算誤差のため厳密にイコールにはなりません)。
長くなってしまったので
続きは次回。今度は独立変数が2個以上(多変量)の場合を考え、さらに回帰式を統計的に扱う方法を見ていきます。
次→【統計検定2級・準1級】Pythonで回帰分析実習(2) - Qiita
-
ここでの「埼京線」は旅客案内上の「埼京線」(大崎~大宮)ではなく、正式路線名が「赤羽線」の区間(池袋~赤羽)のみを指していることが、出典ページの脚注(*C)で示されています。 ↩