はじめに
先日、統計検定2級の試験を受けてきました。
【統計検定2級】2019年11月受験レポート - Qiita
その試験勉強のために、推定・仮説検定を復習していました。
大学は理系だったので共通科目として授業は受けましたが、正直今となっては記憶があいまいに…。
推定や仮説検定でよく使う、正規分布以外の「○○分布」がどうつながっているのか完全に忘れていたので、この機会に代表的なものを整理してみました。
((標本)平均・分散や、正規分布の基本的な性質などの知識を前提とします)
正規分布ファミリーの全体像
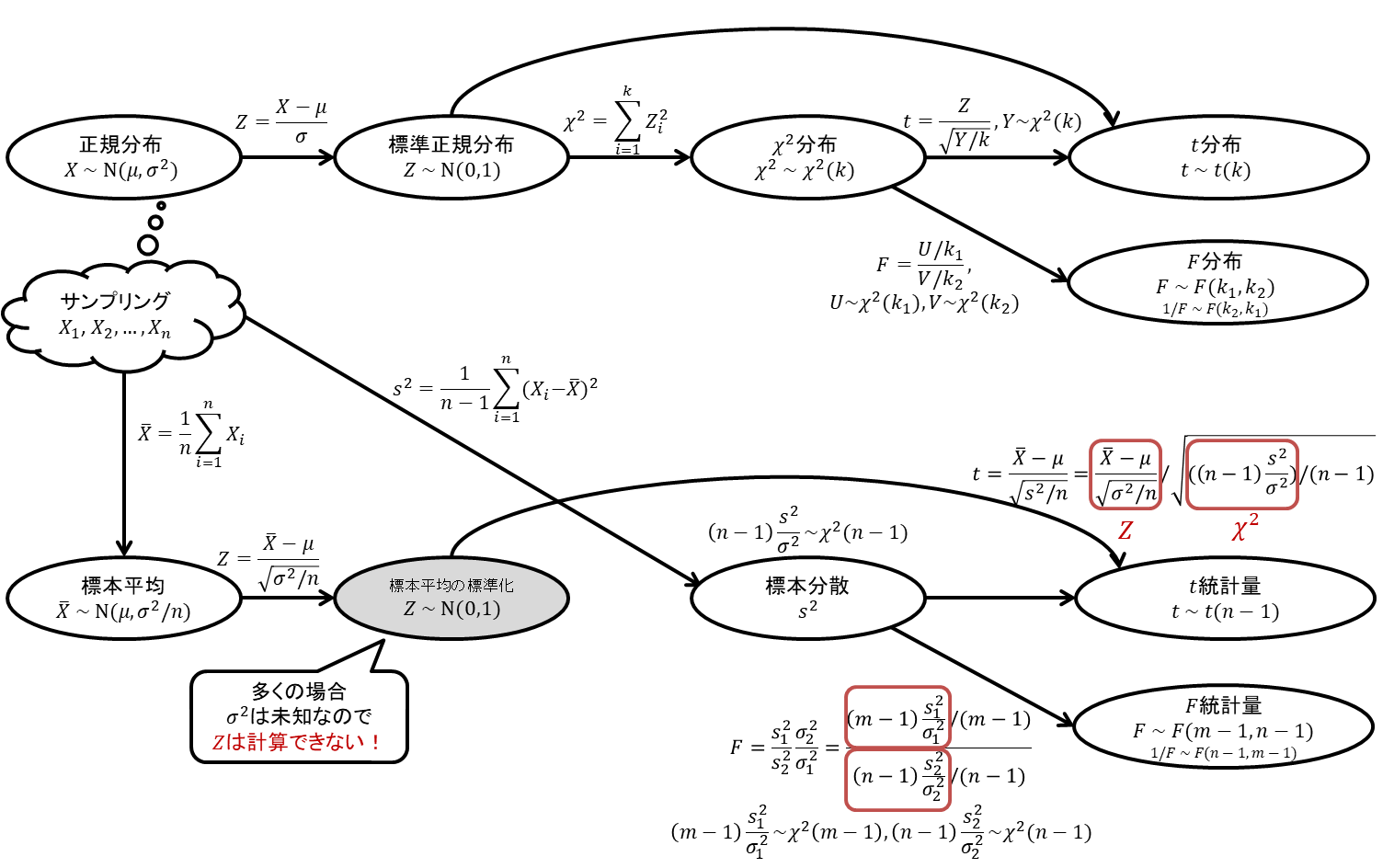
正規分布および正規母集団から派生する諸々の確率分布や統計量の相関図を、画像1枚にまとめてみました。
自分で勝手に「正規分布ファミリー」と呼んでいます。
(あまり厳密性は追求しません。感覚で理解するための概略ということで…)
画像の上の方に正規母集団から色々出てくる確率分布を、下の方に抽出(サンプリング)した標本(サンプル)から得られる統計量と分布を、それぞれまとめています。
また、関係の深い確率変数や統計量を、上下で対応させているつもりです。
2標本問題などは、基本的には1標本問題と似た話になりますし、図が煩雑になりそうですのでここでは割愛します。
これだけ頭に入っていれば、2級の範囲の大半はカバーされていると思いますし、万一本番で忘れても思い出せるんじゃないか?と思っています。
以下、図の内容を順に追っていきます。
以降の節名で (10.1) のようにカッコ書きしているのは、参考文献『統計学入門』の節番号を表しています。
まとめの都合上、必ずしも本に書かれている順番の説明ではありません。
正規分布ファミリーの確率分布
まずは登場人物を揃えましょう。どういうところに出てくるかの説明は後回しにします。
正規分布 (10.1)
ここでのすべての根源、正規分布です。
図の中では平均$\mu$, 分散$\sigma^2$の正規分布を ${\rm N} (\mu, \sigma^2)$ と表しています。
また、$X \sim {\rm N} (\mu, \sigma^2)$で「確率変数$X$が確率分布${\rm N} (\mu, \sigma^2)$に従う」ことを表しています(以降同様です)。
標準正規分布 (10.1)
平均0, 分散1の正規分布を指します。
正規分布に従う確率変数$X$から平均$\mu$を引き、標準偏差$\sigma$(分散の平方根)で割ったもの
Z = \frac{X-\mu}{\sigma} \tag{1}
は、標準正規分布になります。つまり $Z \sim {\rm N} (0, 1)$ です。
カイ二乗分布 (10.3)
「標準正規分布に従う互いに独立な$k$個の確率変数の二乗和」が従う確率分布を、自由度$k$のカイ二乗分布($\chi^2$分布)と呼びます。自由度$k$の$\chi^2$分布を $\chi^2(k)$ と表します。
t分布 (10.4)
「標準正規分布に従う確率変数$Z \sim {\rm N}(0,1)$」を「$\chi^2$分布に従う確率変数$Y \sim \chi^2(k)$を自由度$k$で割ったものの平方根」で割って得られる確率変数を考え、これが従う確率分布を、自由度$k$の(スチューデントの)$t$分布と呼び、$t(k)$ と表します。($Z$と$Y$は独立と仮定します)
t = \frac{Z}{\sqrt{Y/k}} \tag{2}
これを準備しておくことで、$t$統計量に対する理解がしやすくなります(と思います)。
F分布 (10.5)
$\chi^2$分布に従う2つの独立な確率変数 $U \sim \chi^2(k_1), V \sim \chi^2(k_2)$ を、それぞれの自由度で割ったもの同士の比$F$を考えます。
F = \frac{U/k_1}{V/k_2} \tag{3}
この$F$が従う確率分布を自由度$(k_1, k_2)$の$F$分布と呼び、$F(k_1, k_2)$と表します。対称性から $F \sim F(k_1, k_2)$ ならば $1/F \sim F(k_2, k_1)$ となります。
正規分布ファミリーの統計量
正規分布に従う母集団から、互いに独立な$n$個のサンプル$X_1, X_2, \cdots, X_n$を取ります。
これらのサンプル(と、正規母集団という情報)だけを頼りに、母集団に関する統計的性質を解き明かしていきます。…というのが、推定や検定で考えている話なのでした。
標本平均
$n$個のサンプルの算術平均(相加平均)を取ったものです。$\bar{X}$と表記します。
\bar{X} = \frac{1}{n} \sum_{i=1}^n X_i \tag{4}
そのときにたまたま取った$n$個のサンプルによって$\bar{X}$の値は毎回変わりますので、これは確率変数だといえます。その分布は $\bar{X} \sim {\rm N} (\mu, \sigma^2/n)$ です。
標本平均の標準化 (10.2)
$\bar{X}$は正規分布に従いますので、平均を引いて標準偏差で割ることで、標準正規分布を作ることができます。
Z = \frac{\bar{X}-\mu}{\sqrt{\sigma^2 / n}} \tag{5}
しかし、ここで母分散$\sigma^2$の値が分からないという問題に直面します。
推定・検定のときには、「$n$個のサンプルが与えられたときに、母平均$\mu$の取りうる値」などを考えたりするので、$\mu$が分かっている必要はありませんが、そのときに$\sigma^2$が分かっていなくてはどうにもなりません。よって、実問題でこれを使って何かをするということは、ほぼないといっていいでしょう。(問題を解くときに母分散が与えられることはあるかもしれませんが)
標本分散 (10.3)
母分散に対応して、$n$個のサンプルを使って「標本分散」を定義します。
s^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i-\bar{X})^2 \tag{6}
しつこいですが、これも取ったサンプルによって値が変わる確率変数です。ここで分母を$n-1$にすることによって、$s^2$の平均(期待値)が母分散$\sigma^2$と同じになる、という良い性質(不偏推定量)が得られます。
18-3. 推定量の性質 | 統計学の時間 | 統計WEB
この標本分散、母分散で割って$n-1$を掛けると$\chi^2$分布が姿を現します。
(n-1)\frac{s^2}{\sigma^2} = \frac{\sum_{i=1}^n (X_i-\bar{X})^2}{\sigma^2} \sim \chi^2(n-1) \tag{7}
この証明は『統計学入門』には載っていません(感覚的な理解のための説明のみ)が、以下のサイトなどで証明が解説されているので、興味があれば読んでみてください。(統計検定2級なら参考程度でも全然OKのはずです)
不偏分散と自由度n-1のカイ二乗分布 | 高校数学の美しい物語
t統計量 (10.4)
「標本平均の標準化」のところで、サンプルが与えられても$\sigma^2$が分かっていなくてはどうしようもない、と書きました。しかし、$\sigma^2$ではなく$s^2$であればサンプルだけから計算することができます。そこで、式(5)の$\sigma^2$を$s^2$に置き換えたものを考えてみます。
t = \frac{\bar{X}-\mu}{\sqrt{s^2 / n}} \tag{8}
$\sigma^2$と$s^2$は似て非なるものであり、$t$は正規分布にはなりません($\sigma^2$は定数ですが、$s^2$は確率変数です。つまり不確かさが増します)。そこで別の名前をつけ、(スチューデントの)$t$統計量と呼ぶことにします。
この右辺の式をうまく分解すると、$t$が自由度$n-1$の$t$分布に従うことが分かります。
t = \frac{\bar{X}-\mu}{\sqrt{s^2 / n}} = \frac{\bar{X}-\mu}{\sqrt{\sigma^2 / n}} \bigg/ \sqrt{\frac{(n-1)s^2/\sigma^2}{n-1}} \sim t(n-1) \tag{9}
式(5)(7)(9)を組み合わせると、式(2)の形になっていることが分かります。
あとは $Z$ と $s^2$ が独立、すなわち標本平均と標本分散が独立であればよいですね($\bar{X}$と$Z$は定数を加減乗除しただけの関係なので)。この証明は以下などで解説されています(これも統計検定2級の範囲で覚える必要はないと思います)。
[feat.]標本平均と標本分散は独立の証明[ルー大柴] - Qiita
F統計量 (10.5)
2つの正規母集団 ${\rm N}(\mu_1, \sigma_1^2), {\rm N}(\mu_2, \sigma_2^2)$ から、それぞれ$m$個のサンプル $X_1, \cdots, X_m$, $n$個のサンプル $Y_1, \cdots, Y_n$ を独立に取ります。式(4), (6)でこれらの標本平均$\bar{X}, \bar{Y}$および標本分散$s_1^2, s_2^2$を計算します。
\bar{X} = \frac{1}{m} \sum_{i=1}^m X_i \\
\bar{Y} = \frac{1}{n} \sum_{i=1}^n Y_i \\
s_1^2 = \frac{1}{m-1} \sum_{i=1}^m (X_i-\bar{X}) \\
s_2^2 = \frac{1}{n-1} \sum_{i=1}^n (Y_i-\bar{Y})
ここで式(7)より $(m-1)s_1^2/\sigma_1^2 \sim \chi^2(m-1), (n-1)s_2^2/\sigma_2^2 \sim \chi^2(n-1)$ なので、式(3)を使うと
F = \frac{s_1^2/\sigma_1^2}{s_2^2/\sigma_2^2} = \frac{s_1^2}{s_2^2}\frac{\sigma_2^2}{\sigma_1^2} \sim F(m-1, n-1) \tag{10}
となります。特に $\sigma_1^2 = \sigma_2^2$ のときは
F = \frac{s_1^2}{s_2^2} \sim F(m-1, n-1) \tag{11}
ですね。与えられたサンプルから2つの母分散が等しいことを検定するとき(2標本の標本平均の差について調べたいときに、母分散が等しいかどうかで話が変わる)には、帰無仮説として母分散を等しいとおきますので、式(11)の形が使えます。統計検定2級で使うのは式(11)のパターンが多いと思います。
例題
出題数は多くないですが、これらの分布の定義を知っているかを問われることがあります。
以上の関係性が頭に入っていると、こんな問題が解けます。
引用部分の出典はオリジナルの試験問題より。
2017年11月 問9
確率変数が従う分布の名前を答える問題です。
確率変数 $Z_1, Z_2, \cdots, Z_n$ が互いに独立に標準正規分布 ${\rm N}(0,1)$ に従うとき $W = Z_1^2 + Z_2^2+ \cdots + Z_n^2$ は自由度$n$の(ア)分布に従う。
これは「カイ二乗」分布の定義通りですね。
また、標準正規分布 ${\rm N}(0,1)$に従う確率変数$Z$が$W$と独立であれば $\frac{Z}{\sqrt{W/n}}$ は自由度$n$の(イ)分布に従う。
ここで$W$はカイ二乗分布に従いますので、式(2)の「$t$」分布の定義です。最初の画像だと右上辺りにありますね。$t$検定で計算する$t$統計量も、この$t$分布に従うのでしたね。
さらに、確率変数$W_1,W_2$が互いに独立に自由度$m_1,m_2$の(ア)分布に従うとき $\frac{W_1/m_1}{W_2/m_2}$ は自由度 $(m_1, m_2)$ の(ウ)分布に従う。
式(3)の「$F$」分布の定義ですね。
さらに続きの問題で
確率変数 $Z_1, Z_2, \cdots, Z_{30}$ が互いに独立に標準正規分布 ${\rm N}(0,1)$ に従うとする。$
Y = \frac{\sum_{i=1}^{20} Z_i^2 / 20}{\sum_{i=21}^{30} Z_i^2 / 10}$としたとき、$P(Y \leq a) = 0.05$ となる $a$ はいくらか。(選択肢は略)
$Y$の分子の $\sum_{i=1}^{20} Z_i^2$ は $\chi^2(20)$ に従い、分母の $\sum_{i=21}^{30} Z_i^2$ は $\chi^2(10)$ に従いますね。そして題意より両者は互いに独立になるので、式(3)の$F$分布の定義より、$Y \sim F(20,10)$ となります。
ところが、実際に求めるべき $a$ を付表から探そうと思っても、付表では「上側確率」が0.05, 0.025になる点しか与えられていません。$Y, a$は正としてよいので、$P(Y \leq a) = P(1/Y \geq 1/a)$ と書き換え、さらに$F$分布の定義に立ち返ると
\frac{1}{Y} = \frac{\sum_{i=21}^{30} Z_i^2 / 10}{\sum_{i=1}^{20} Z_i^2 / 20} \sim F(10,20)
とわかります。この形であれば、付表から探すことができます。
$P(1/Y \geq 1/a) = 0.05$ から $1/a = 2.348$ となるので、$a = 1/2.348$ です。
2017年6月 問10
確率変数 $X_1, X_n$ は互いに独立に標準正規分布に従うものとし、$W_n = X_1^2 + X_2^2+ \cdots + X_n^2$ とする。
〔1〕 $W_1 \geq w$ となる確率が0.05となるような $w$ の値として、次の(1)~(5)のうちから最も適切なものを一つ選べ。(選択肢は略)
$W_n$ は題意より $\chi^2(n)$ に従いますね。カイ二乗分布の定義通りです。
$n=1$ の場合を考えると、 $W_1$ は $\chi^2(1)$ に従います。付表からこの値を探すと 3.84 となります。
どうしてもカイ二乗分布を思い出せなければ、$P(W_1 \geq w) = P(X_1^2 \geq w) = P(|X_1| \geq \sqrt{w}) = 2 \times P(X_1 \geq \sqrt{w})$ と考えて、標準正規分布のパーセント点を付表から探してくるのもよいと思います。(次の〔2〕ではカイ二乗分布が分からないと詰まってしまうのですが…)