#ハノイの塔
##ハノイの塔とは
ハノイの塔は、フランスの数学者エドゥアール・リュカが1883年に発売したゲーム『ハノイの塔』がルーツである。
https://ja.wikipedia.org/wiki/%E3%83%8F%E3%83%8E%E3%82%A4%E3%81%AE%E5%A1%94#%E7%94%B1%E6%9D%A5
プログラムとは関係のないパズルの一種でハノイの塔のオモチャもあるようです。
プログラムとは関係ありませんがプログラムで解く題材としてもよく扱われる問題の一種です。
以下のようなゲームです。
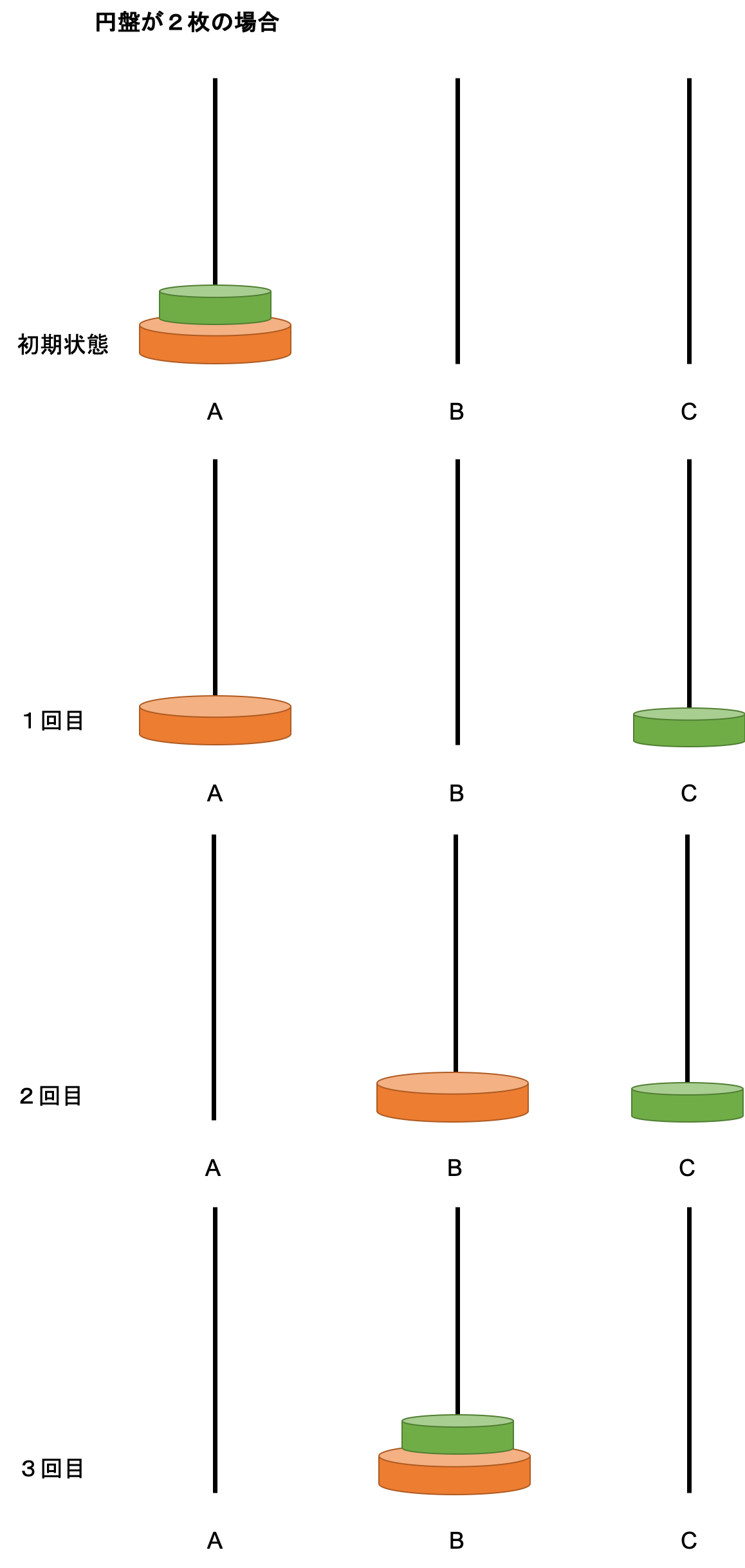
３本の棒A、B、Cがあり、棒Aに何枚かの大きさの異なる円盤が下から大きい順に棒を通して重ねられています。
これを以下のルールに従って円盤をAからBに移動させます。
- ルール
- １回に一枚の円盤しか動かせない。
- 移動途中も常に大きい方の円盤が下になるように積む。
- 棒A、B、C以外の場所に移動させてはいけない
（例）円盤が２枚の場合
##問題
以下表示例のような、ハノイの塔でN枚の円盤を移動させる手順を表示する再帰関数を作成してください。
※Nが０以下の場合は何も表示しなくてかまいません。
数字はそれぞれ円盤を表し、小さい円盤から順に1,2,3,...とします。
表示例(N=2の場合)
1の円盤をAからCに移動
2の円盤をAからBに移動
1の円盤をCからBに移動
表示例(N=3の場合)
1の円盤をAからBに移動
2の円盤をAからCに移動
1の円盤をBからCに移動
3の円盤をAからBに移動
1の円盤をCからAに移動
2の円盤をCからBに移動
1の円盤をAからBに移動
回答例はこちら
##ヒント
解き方のヒントを載せているので難しい場合は参考にしてみてください。
【注意】
回答例のページと同じページに掲載しています。
下の方に回答例が書かれているので見たくない人は注意してページをスクロールしてください。
#最後に
別の問題は以下に掲載しています。
また本記事とは別でプログラミング未経験からiOSアプリ開発が行えるようになることを目的とした記事を連載しています。
連載も以下にまとめていますのでそちらも是非もご覧ください。
http://naoyalog.com/