【プログラミング初心者】Swift練習問題~ハノイの塔~回答例

ハノイの塔

ヒント

ヒント１

プログラムを組むときは小さな例をあげてみて、法則性を探すことが重要です。
紙に書いてみるのも１つの手です。

まずハノイの塔における最小単位はN=1です。
N=1の実行は以下になるはずです。

N=1の場合

1の円盤をAからBに移動

これでは法則がわからないので１つ進めてN=2の場合を考えます。
N=2の実行例は以下になります。

N=2

1の円盤をAからCに移動
2の円盤をAからBに移動
1の円盤をCからBに移動

まだ法則が分かりづらいのでN=3も考えてみます。
N=3の実行例は以下になります。

1の円盤をAからBに移動
2の円盤をAからCに移動
1の円盤をBからCに移動
3の円盤をAからBに移動
1の円盤をCからAに移動
2の円盤をCからBに移動
1の円盤をAからBに移動

ここまできたら法則がある程度見えるようになります。

まず注目したいのが、それぞれの場合の真ん中の出力です。

-- N=1の場合 --
1の円盤をAからBに移動
-- N=2の場合 --
2の円盤をAからBに移動
-- N=3の場合 --
3の円盤をAからBに移動

必ず真ん中で一番大きな円盤を「AからBに移動」させていることがわかります。
このあたりに解決の糸口がありそうです。

N=2、N=3の場合で一番大きな円盤を「AからBに移動」させた状況を図に書いてみます。

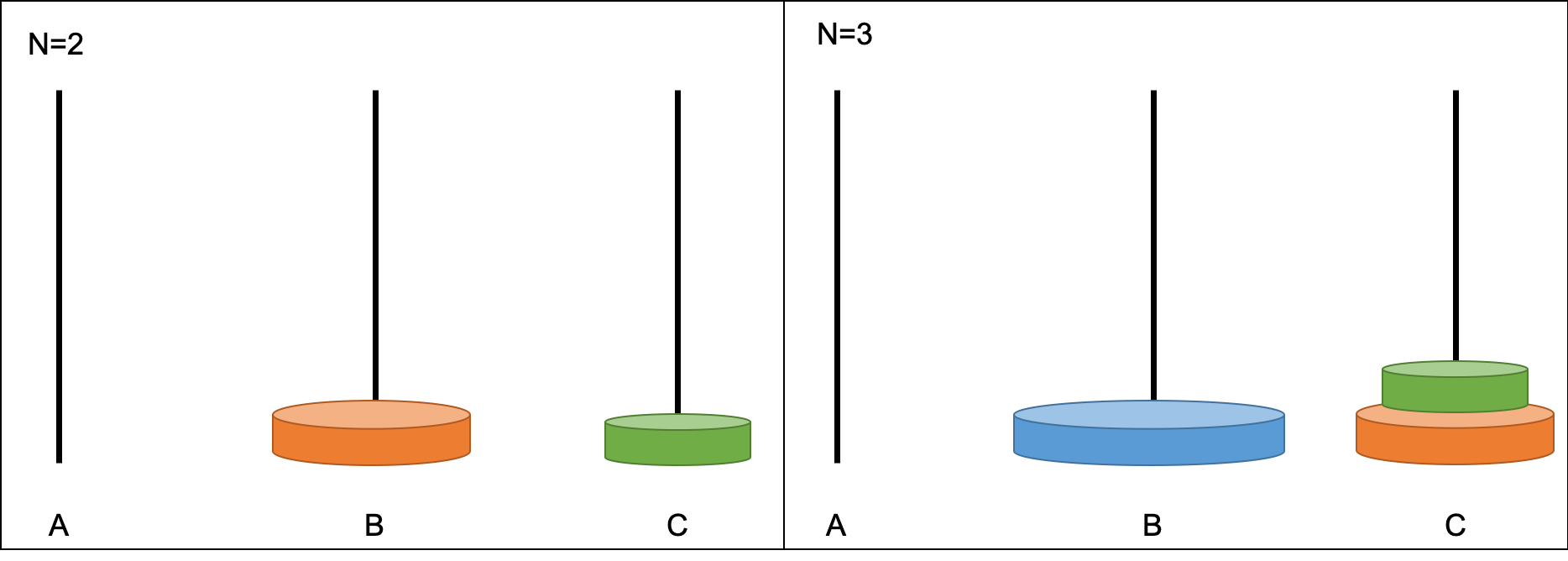
図を見るとわかるようにCにN-1個の円盤が積み重なっています。

ここまでの法則がわかったら、次はどうすれば棒CにN-1個の円盤を移動させれるか、さらにどうすれば棒Cから棒Bに移動させればいいのかを考えていきましょう。

ヒント１はここまでです。
次項からはヒント２となります。

ヒント２

まずは前項のヒント１を読んでください。

ではどうすればN-1個の円盤を棒Aから棒Cに円盤を移動させられるか考えてみましょう。

N=3について考えます。
N=3のとき、上部２個の円盤を棒Aから棒Cに移動させる手順は以下の通りです。

上部２個を移動させる手順

1の円盤をAからBに移動
2の円盤をAからCに移動
1の円盤をBからCに移動

２個の移動なので参考にN=2の全手順を見てみましょう。

N=2の手順

1の円盤をAからCに移動
2の円盤をAからBに移動
1の円盤をCからBに移動

非常によく似ているとは思いませんか？
BとCを入れ替えれば完全に同じ手順になります。

これら２つは目的の場所は違いますが、同じ２個の円盤を同じルールで目的の場所に移動させているのですから手順が同じになるのは当然です。

同じ処理なので目的の場所を入れ替えることさえできれば再帰関数でN-1という値を与えてあげれば解決できそうです。

次は後半のN-1個の円盤を棒Cから棒Bに移動させる方法について考えます。
N=3の後半手順は以下となります。

N=3の後半手順

1の円盤をCからAに移動
2の円盤をCからBに移動
1の円盤をAからBに移動

これもやはり円盤２個の移動なのでN=2の手順と似てますね。
棒Aと棒Cを入れ替えてあげることができれば、これも再帰関数でN-1という値を与えて解決できそうです。

ヒント１、ヒント２で以下の法則性は見つけられました。

1. 棒Aから棒CのN-1個の円盤を移動させる
2. 棒Aから棒BにNの円盤を移動させる
3. 棒Cから棒BにN-1個の円盤を移動させる

あとはどう関数で表現するか考えるだけです。
どうすれば目標の棒を棒Bと棒Cに入れ替えられるか。
どうすれば開始の棒を棒Aと棒Cに入れ替えられるか。
このあたりを考えてみましょう。

ヒント２はここまでです。
次項からはヒント３となります。

ヒント３

ヒント１、ヒント２の考えが前提となります。

法則性がわかったのでどうやって棒を入れ替えていくか考えます。

ここまでで各状態におけるパラメータを洗い出してみます。

• 初期状態
  • 動かす円盤の個数：N個
  • 開始の棒：A
  • 目標の棒：B
  • どちらでもない棒：C
• 前半の移動
  • 動かす円盤の個数：N-1個
  • 開始の棒：A
  • 目標の棒：C
  • どちらでもない棒：B
• 後半の移動
  • 動かす円盤の個数：N-1個
  • 開始の棒：C
  • 目標の棒：B
  • どちらでもない棒：A 以上４つが状況に応じて変わることがわかります。

このように状況に応じて変わるものは引数として扱えば変更できます。
つまり以下のように定義してあげます。

func solveHanoi(numberOfDisk: Int, from fromStickName: String, to toStickName: String, buffer bufferStickName: String) {
    ...
}

solveHanoi(numberOfDisk: 3, from: "A", to: "B", buffer: "C")

それぞれの引数の意味は以下の通りです。

• numberOfDisk
  • 円盤の個数
• fromStickName
  • 開始となる棒の名前
• toStickName
  • 目標となる棒の名前
• bufferStickName
  • 開始/目標のどちらでもない作業中に使う棒の名前

これで棒を入れ替えることが可能です。
あとは呼び出しのときにそれぞれの棒の名前を指定し、関数内部でその値を入れ替えてあげます。

ヒント２はここまでです。
次項からは回答例となります。

回答例

func solveHanoi(numberOfDisk: Int, from fromStickName: String, to toStickName: String, buffer bufferStickName: String) {
    if numberOfDisk <= 0 {
        return
    }
    solveHanoi(numberOfDisk: numberOfDisk - 1, from: fromStickName, to: bufferStickName, buffer: toStickName)
    print("\(numberOfDisk)の円盤を\(fromStickName)から\(toStickName)に移動")
    solveHanoi(numberOfDisk: numberOfDisk - 1, from: bufferStickName, to: toStickName, buffer: fromStickName)
}

解説

考え方はヒントで説明しているのでそちらを参照してください。

if numberOfDisk <= 0 {
    return
}

この条件は終了条件とエラー処理両方を表します。
実際の終了条件としては移動させる円盤がなくなったタイミングとなるのでnumberOfDisk == 0となります。

solveHanoi(numberOfDisk: numberOfDisk - 1, from: fromStickName, to: bufferStickName, buffer: toStickName)

まずは前半処理です。
N-1個の円盤移動を考えるのでnumberOfDiskにnumberOfDisk - 1を与えます。
棒Bと棒Cを入れ替えるのでfromStickNameとbufferStickNameの値を入れ替えています。

print("\(numberOfDisk)の円盤を\(fromStickName)から\(toStickName)に移動")

ここは一番大きな円盤となるNを移動させています。

solveHanoi(numberOfDisk: numberOfDisk - 1, from: bufferStickName, to: toStickName, buffer: fromStickName)

後半処理です。
円盤はN-1、開始が棒C、目標が棒B、作業中に使う棒が棒Aとなるようにそれぞれ引数に与えます。

これで呼び出すと再帰処理が走り、ハノイの塔の手順が求まります。

【注意】
ハノイの塔の移動回数は2^n−1回です。(2^nは2のn乗という意味)
あまり大きい値を入れると指数関数的に大きくなり処理が終わらないので多くてもN=10(1023回)までにする方が無難かと思います。