切上と切捨の話。
ここ最近ずーっと頭のなかにあったもやもやがようやく取れた!!!
ので記事にしてみる。
結論
ceil(A)-1 == floor(A-1)が成立する条件は、
- Aが整数の場合
です。
といってもなんのこっちゃわからん!となると思うので例題。
例題
1:2.8~4.2で整数は何個あるでしょう?
2:2.0~4.2で整数は何個あるでしょう?
3:14~21で5の倍数は何個あるでしょう?
4:10~21で5の倍数は何個あるでしょう?
5:9mの丸太を3mずつ切り続けられるまで切る時、切れ目は何個あるでしょう?
6:9mの丸太を2mずつ切り続けられるまで切る時、切れ目は何個あるでしょう?
7:9mの丸太を1mずつ切り続けられるまで切る時、切れ目は何個あるでしょう?
解説1
1:2.8~4.2で整数は何個あるでしょう?
この問題は、
「2.8」を切上げて「3」
「4.2」を切捨てて「4」
とすることで
- 3~4で整数は何個あるでしょう?
という問題に帰着できます。
よって、4 - 3 + 1(調整) = 2個 が答えとなります。
解説2
2:2.0~4.2で整数は何個あるでしょう?
これは左の切上げの部分が「2」と整数なので簡単ですね!
よって、4 - 2 + 1(調整) = 3個 が答えとなります。
解説3
3:14~21で5の倍数は何個あるでしょう?
この問題は大きく2つの解法があると思います。
解法1(1を引いて切捨)
累積和の時の考え方に似ていますが、
「21」の5の倍数の個数 - 「13」(=14-1)の5の倍数の個数

と考えることで、
- 21/5の切捨 = 4
- 13/5の切捨 = 2
よって、4 - 2 = 2個 が答えとなります。
解法2
14~21を5で割って整数の数を数える問題に帰着させるやり方です。
すると、
1:2.8~4.2で整数は何個あるでしょう?
と同じ問題になります。
よって、4 - 3 + 1(調整) = 2個 が答えとなります。
解説4
4:10~21で5の倍数は何個あるでしょう?
解法1(1を引いて切捨)
- 9/5の切捨 = 1
よって、4 - 1 = 3個 が答えとなります。
解法2
10~21を5で割って整数の数を数える問題に帰着させると、
2:2.0~4.2で整数は何個あるでしょう?
と同じ問題になります。
よって、4 - 2 + 1(調整) = 3個 が答えとなります。
ここまでのまとめ
1:2.8~4.2で整数は何個あるでしょう?
2:2.0~4.2で整数は何個あるでしょう?
3:14~21で5の倍数は何個あるでしょう?
4:10~21で5の倍数は何個あるでしょう?
3や4のような問題をとく場合は、解法1を使えばすべて切捨だけで考えることができます。
また、切上は調整分の考慮が必要ですし、
プログラム的にも、pythonでは切捨を//のみで表すことができるので、できればすべて解法1の「1を引いて切捨」で処理したいです。
# 3:14~21で5の倍数は何個あるでしょう?
# 解法1(1を引いて切捨)
ans = 21//5
ans -= 13//5
print(ans) #2
# 解法2(切上-1)
import math
ans = 21//5
ans -= math.ceil(13/5)-1 #ans -= -(-13//5)-1とするのも一つ。
print(ans) #2
しかし・・・
小数の場合は、「1を引いて切捨」が使えない!!!
です。
実際に試してみましょう。
答え「2」
となるはずの1問目の問題を解法1,2でそれぞれ解いてみます。
# 1:2.8~4.2で整数は何個あるでしょう?
# 解法1(1を引いて切捨)
ans = 4.2//1
ans -= 1.8//1
print(ans) #3.0 →本当は2が正しい!!!!!!!!!!!
# 解法2(切上-1)
import math
ans = 4.2//1
ans -= math.ceil(2.8/1)-1
print(ans) #2.0 →正しい結果となった。
改めて結論
ceil(A)-1 == floor(A-1)が成立する条件は、
- Aが整数の場合
です。
1:2.8~4.2で整数は何個あるでしょう?
2:2.0~4.2で整数は何個あるでしょう?
3:14~21で5の倍数は何個あるでしょう?
4:10~21で5の倍数は何個あるでしょう?
1→「2.8」が小数なので、ceil(A)-1 == floor(A-1)は成り立ちません。
よって、切上を素直に使いましょう。
小数の世界に「1」という(次元の違う)整数を勝手に引いたりしたらそれはおかしくなるわ!
2,3,4→「2.0」「14」「10」が整数なので、ceil(A)-1 == floor(A-1)が成り立ちます。
よって、「1を引いて切捨」の考えが可能です!!!
※もちろん、切上を使っても解けます。
解説5,6,7
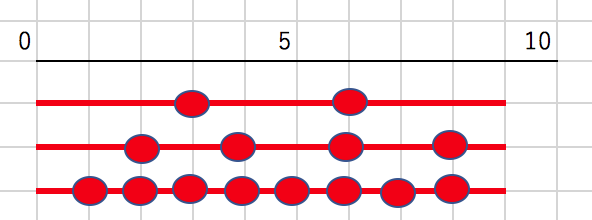
5:9mの丸太を3mずつ切り続けられるまで切る時、切れ目は何個あるでしょう?
6:9mの丸太を2mずつ切り続けられるまで切る時、切れ目は何個あるでしょう?
7:9mの丸太を1mずつ切り続けられるまで切る時、切れ目は何個あるでしょう?
考察すると、切れ目の個数は「切上-1(調整)」で求めることができるとわかります。
そして、「切上-1」といえば「1を引いて切捨」です!
今回は「9」が整数なため、「1を引いて切捨」で答えを求めることができます!!!
よってそれぞれ5,6,7の答えは、
# 5
8//3 = 2
# 6
8//2 = 4
# 7
8//1 = 8
となります!!!
すごい!!!
この凄さ、感動!!!伝わるかな・・・伝わってほしい!!!
おまけ(練習問題)
ぜひ解いてみましょう!
ABC131 C - Anti-Division (Diff:518)
ABC174 E - E - Logs (Diff:1227)
おわり!