はじめに
人工衛星は太陽光から発電し,各種ミッションを実現しています.人工衛星を運用する際,**機体が地球の影に隠れてしまう食(地球食)**が発生します.このため,次のようなことに注意する必要があります.
- 太陽光から発電できないため,バッテリーから給電する必要がある
- 影の領域では温度が急激に低下するため,各機器のヒータを起動しておく必要がある
ここでは周回衛星の食時間を求めてみたいと思います.
食が発生しない場合
衛星高度$H$,軌道傾斜角$\gamma$の円軌道の衛星が半径$R$の地球を周回する状況を考えます.なお,地球の影の領域は円筒状になるとします.
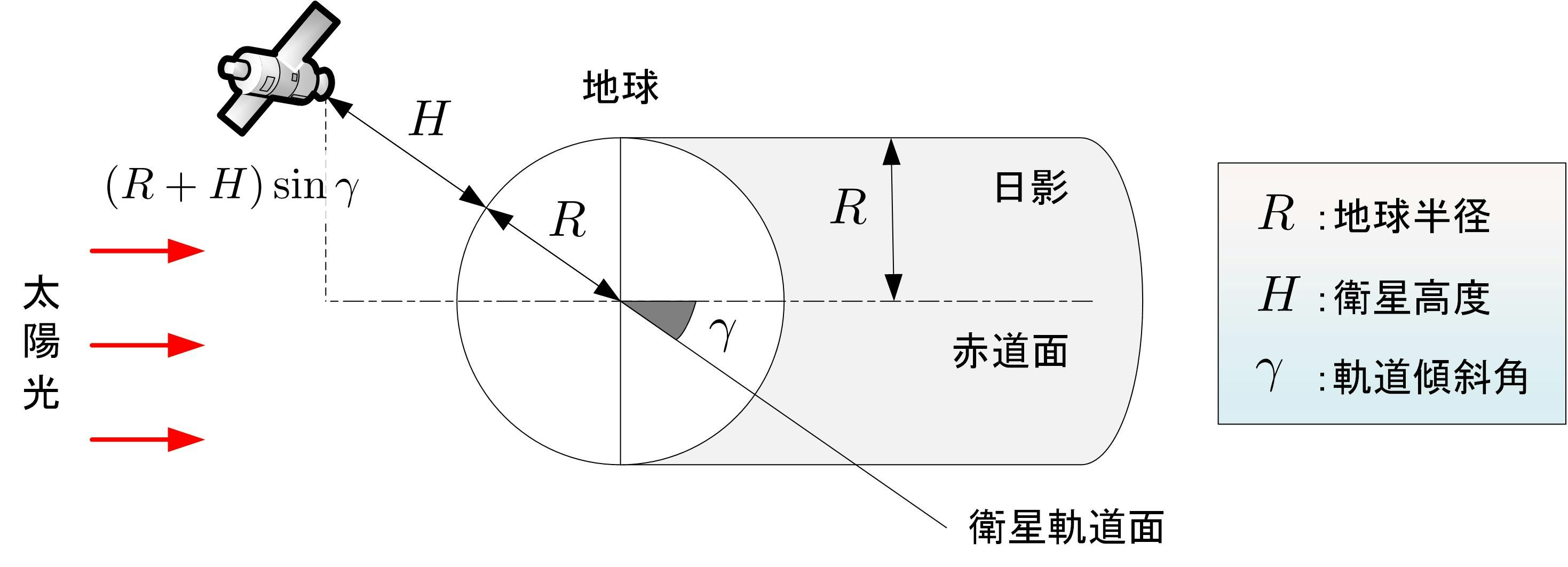
この衛星が次の条件
$$
\begin{align}
(R+H)\sin{\gamma}&>R \
\rightarrow R+H &> \frac{R}{\sin{\gamma}}
\end{align}
$$
を満たすときには,衛星は地球の影に入らず食は発生しません.
食が発生する場合
一方で,
$$
\begin{align}
(R+H)\sin{\gamma}&<R \
\rightarrow R+H &< \frac{R}{\sin{\gamma}}
\end{align}
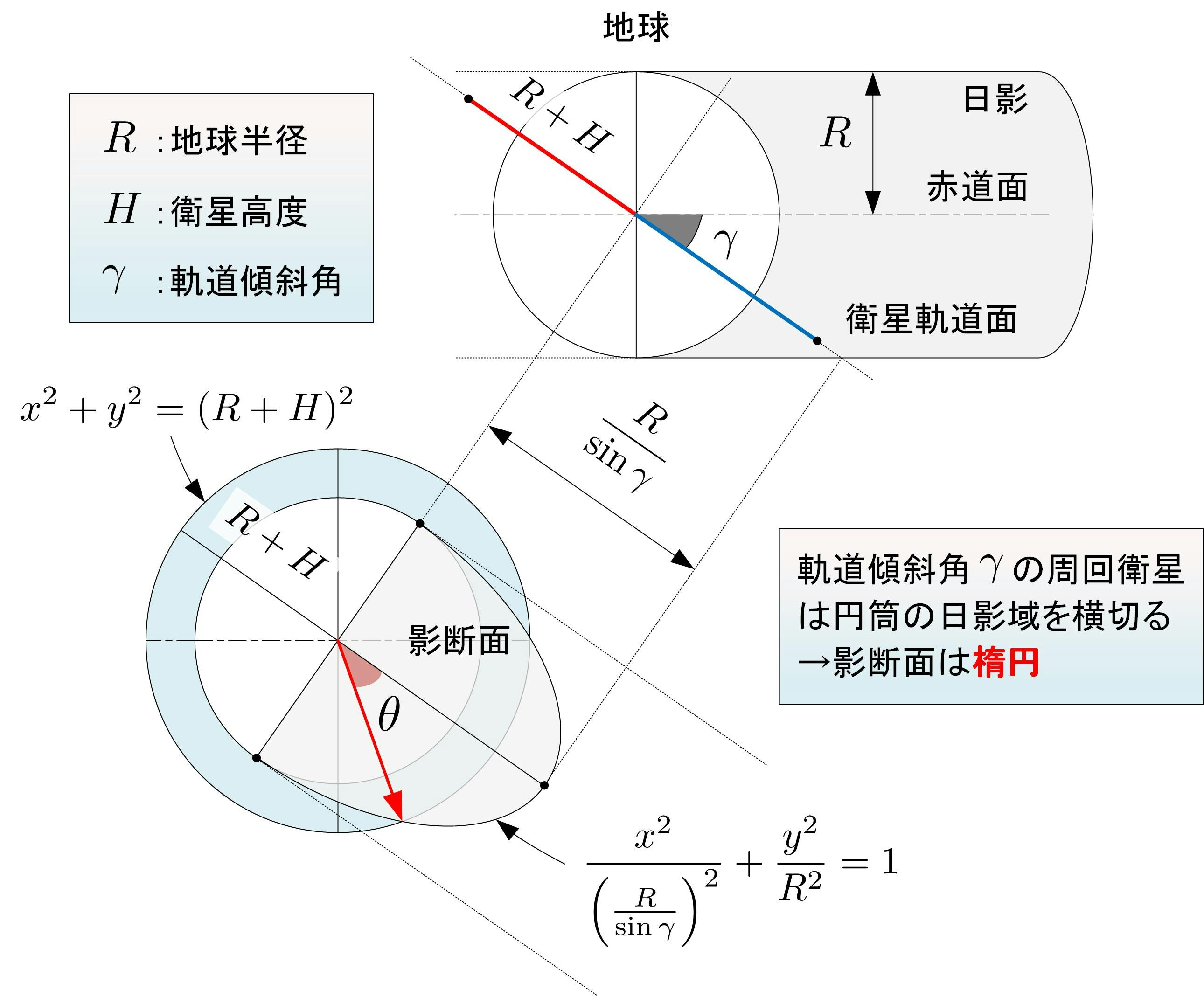
$$の場合は食が発生することになります.衛星の円軌道の式を次のような極座標で表現します.
$$
x=(R+H)\cos{\theta},~~y=(R+H)\sin{\theta} \tag{1}
$$
また,衛星は影の領域を斜めに横切ることになりますから,下図に示すように影の断面は楕円となります.影の円筒を円軌道が切る楕円の式はパラメータ$t$を用いて次のように表現します.
$$
x=\frac{R}{\sin{\gamma}}{\cos{t}},~~y=R\sin{t} \tag{2}
$$
式(1)と(2)の座標が等しいとして,$\theta$を求めてみます.
$$
\begin{cases}
(R+H)\cos{\theta}&=\cfrac{R}{\sin{\gamma}}{\cos{t}}\
(R+H)\sin{\theta}&=R\sin{t}
\end{cases}
$$
途中式は省略しますが,$t$を消去するように変形すると
$$
\cos{\theta}=\frac{\sqrt{2RH+H^2}}{\cos{\gamma}(R+H)} \tag{3}
$$
が得られます.
計算例
軌道高度$h=1,000~\rm{km}$の円軌道の衛星の食時間を求めてみます.上で示した図において,$\gamma=0$の場合,影の形は長方形となります.これを利用すれば日陰に入る角度$2\theta$が簡単に計算できます.式(3)において$\gamma=0$とおけば,
$$
\begin{align}
\cos{\theta}&=\frac{\sqrt{2RH+H^2}}{\cos{\gamma}(R+H)}=\frac{\sqrt{2\times 6378\times 1000+1000^2}}{(6378+1000)}\simeq 0.5027 \
\therefore~\arccos{\theta}&=59.8^\circ
\end{align}
$$
と計算できます.ここで,衛星が1周回する時間(周期)$T$は
$$
\begin{cases}
v=\sqrt{\cfrac{MG}{R+H}} \
T=\cfrac{2\pi}{v}(R+H)
\end{cases}
$$
を利用して,
$$
T=2\pi\sqrt{\frac{R+H}{MG}}(R+H)\simeq 105~\rm{min}
$$
と表現できます$^{*1}$.
以上から,食時間$T_s$は次のように計算できます.
$$
T_s=\frac{2\theta}{360}\times T=\frac{2\times 59.8^\circ}{360}\simeq35~\rm{min}
$$
参考
*1:衛星の速度・周期の計算法は以下でも紹介しています.
https://qiita.com/epppJones/items/73fe11025b29d990ce1e
木田,小松,川口,人工衛星と宇宙探査機,コロナ社,2011.