深層学習Day1
Section1:入力層~中間層
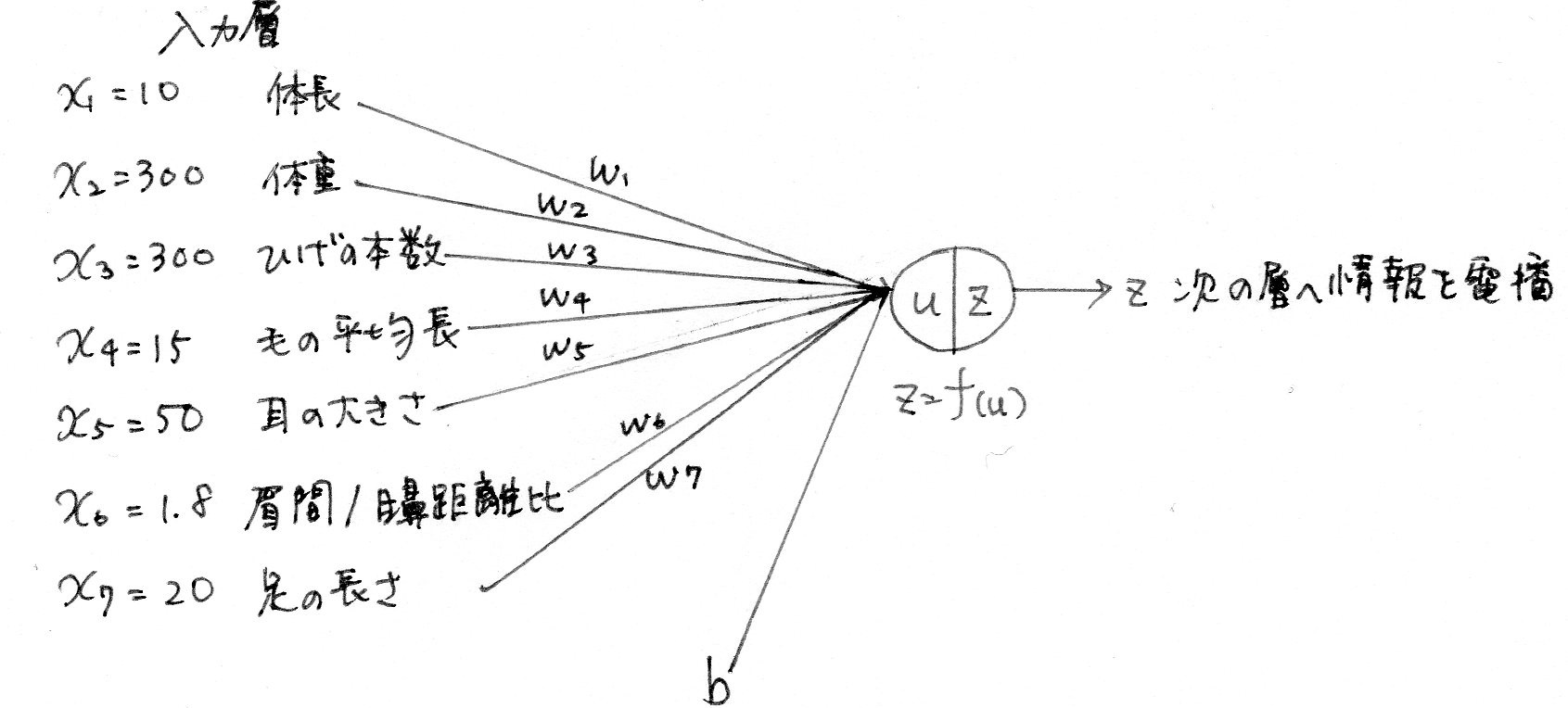
§ 入力層 ・ 最初に情報を受け取る層 § 中間層(隠れ層) ・ 入力層から情報を受け継ぎ、さまざまな計算を行う ・ 中間層が多いほど複雑な分析ができる 入力層、中間層のイメージ
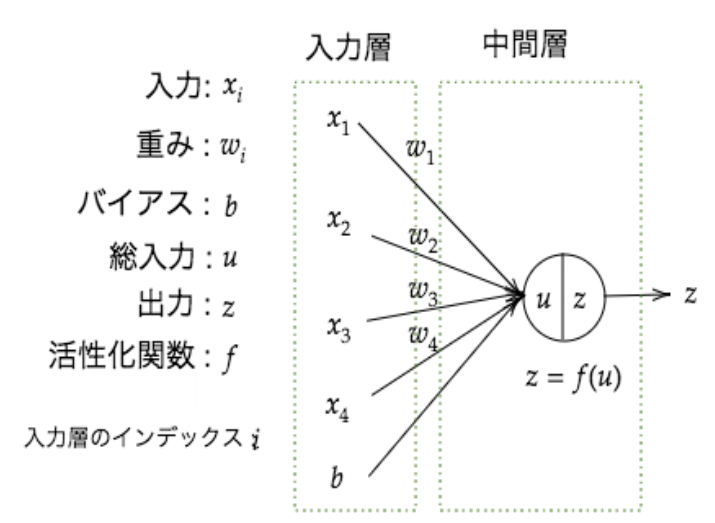
※ ここでは中間層は1層しか描かれていないが、実際は何層にも重ねて処理される
◆ 中間層での計算
$u = w_1x_1+w_2x_2+w_3x_3+w_4x_4+b$
ここで
$W=\left[\begin{array}{l}w_1\\w_2\\w_3\\w_4\end{array}\right],,X=\left[\begin{array}{l}x_1\\x_2\\x_3\\x_4\end{array}\right]$
とすると
$,,,,,= WX+b $と書くことができる
◆ 計算の最終的な目的
入力値から目的とする出力値に変換する数学モデルを構築すること
モデル構築時、$w,$(重み)、$b,$(バイアス)は未知の値なので計算の中で最適化する
○ この数式をPythonで書け
$u=w_1x_1+w_2x_2+w_3x_3+w_4x_4+b=WX+b$
$u=np.dot(X,W)+b$
※ np=numpy
※ 数式とコードの$w_1x_1+w_2x_2+w_3x_3+w_4x_4$部分は行列の積の形になる
※ 1行×1行の行列の積を求める場合は転置が必要だが、
numpyのdot関数では不要
1-1のファイルから中間層の出力を定義しているソースを抜き出せ

・ 中間層でも活性化関数が使用される
Section2:活性化関数
§ 活性化関数 ・ ニューラルネットワークにおいて、次の層への出力の大きさを決める非線形の関数 ・ 入力値の値によって、次の層への信号のON/OFFや強弱を定める働きをもつ ・ 活性化関数を導入することで表現力豊かなモデルを構築できる ◇ 確認テスト
○ 線形と非線形の違い
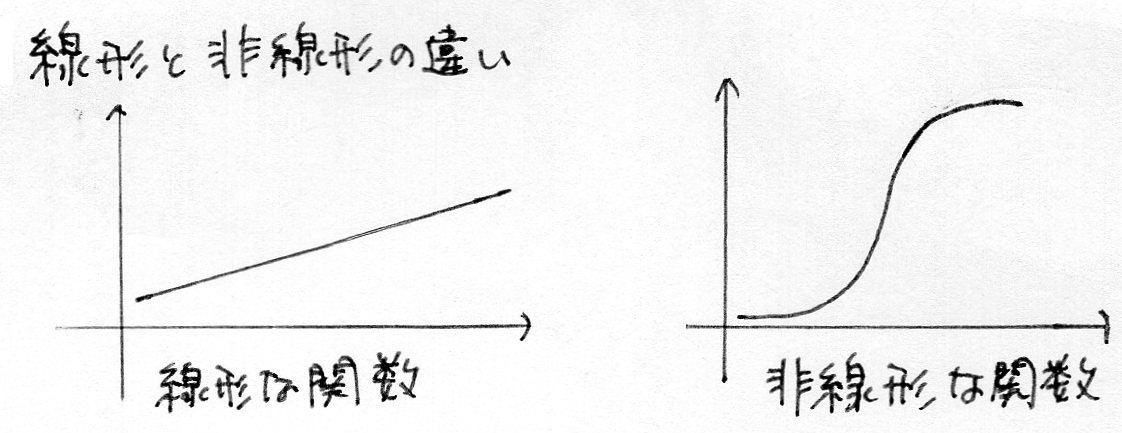
※ 線形な関数は
・ 加法性:$f(x+y)=f(x)+f(y)$
・ 斉次性:$f(kx)=kf(x)$
を満たす(非線形な関数は加法性、斉次性を満たさない)
§ 中間層用の活性化関数
◆ ステップ関数
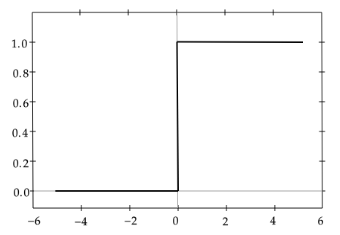
$f(x)=\left\{\begin{array}{l}1,,(x≧0)\\0,,(x<0)\end{array}\right.$
・ しきい値を超えたら発火する関数
・ 出力は常に1か0
・ パーセプトロン(ニューラルネットワークの前身)で利用された関数
【課題】
0 -1間の間を表現できず、線形分離可能なものしか学習できなかった
◆ シグモイド関数
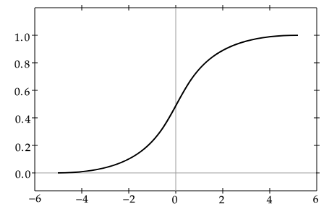
$f(u)=\frac{1}{1+e^{-u}}$
・ 0~1の間を緩やかに変化する関数
・ ステップ関数と違い信号の強弱を伝えられる
・ 予想ニューラルネットワーク普及のきっかけとなった
【課題】
大きな値では出力の変化が微小なため、勾配消失問題を引き起こす事があった
● pythonでの実装
def sigmoid(x):
return 1/(1 + np.exp(-x))
◆ RELU関数
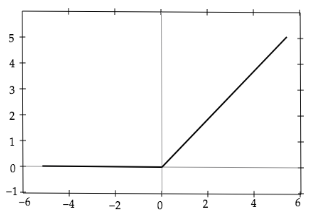
$f(x)=\left\{\begin{array}{l}x,,(x>0)\\0,,(x≦≦0)\end{array}\right.$
・ 今最も使われている活性化関数
・ 勾配消失問題の回避とスパース化に貢献することで良い成果をもたらしている
● pythonでの実装
def relu(x):
return np.maximum(0, x) #npはnumpyのこと
◇ 確認テスト
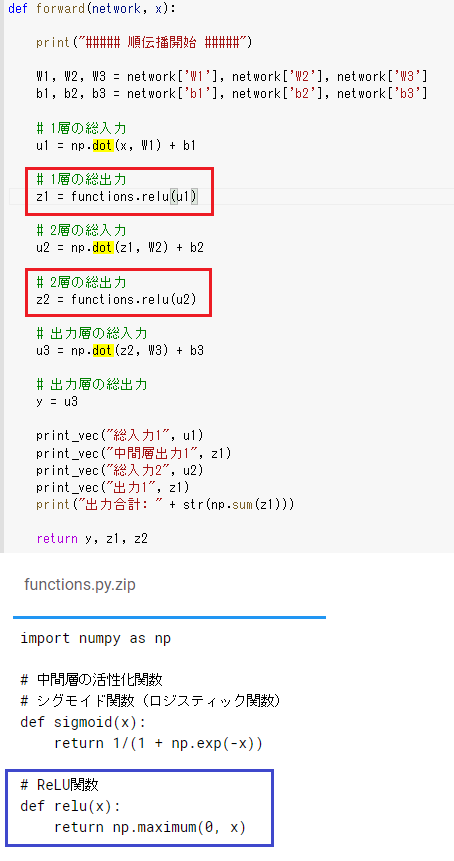
○ ソースコードの中で活性化関数が使用されている場所
・ 赤枠の部分が活性化関数が使用されている場所
・ 青枠は実際の活性化関数の定義
Section3:出力層
§ 出力層 ・ 最終的に欲しい内容を出力する層 § 誤差関数
・出力層が出力した内容と本来の答えとの差(誤差)による関数
・分類問題はクロスエントロピー誤差
回帰問題は平均二乗誤差をそれぞれ用いる
§ 二乗誤差を使った誤差の計算
$E_n(w)=\frac{1}{2}\displaystyle\sum^J_{j=1}(y_j-d_j)^2=\frac{1}{2}||(y-d)||^2$
$ y=答え, d=予測値$
◇ 確認テスト
○ 誤差計算で引き算ではなく二乗する意味
・ 引き算だと各答えと予測の誤差が、プラスの誤差とマイナスの誤差があり
打ち消しあってしまうため
$○ 式E_n(w)=\frac{1}{2}\displaystyle\sum^J_{j=1}(y_j-d_j)^2=\frac{1}{2}||(y-d)||^2の\frac{1}{2}の意味$
・$\frac{1}{2}$は後に誤差関数を微分するため(計算が楽になるように)
§ 出力層の活性化関数
・ 信号の大きさ(比率)はそのままに変換
・ 分類問題の場合、出力層の出力は0 ~ 1 の範囲に限定し、確率の総和を1とする
必要がある
・ 出力層と中間層で利用される活性化関数が異なる
・ 問題に応じて用いる活性化関数は決まっている
| 回帰 | 二値分類 | 多クラス分類 | |
| 活性化関数 | 恒等写像 $f(u)=u$ |
シグモイド関数 $f(u)={1+e^{-u}}$ |
ソフトマックス関数 $f(i,u)=\frac{e^{u_i}}{\sum^K_{k=1}e^{u_k}}$ |
| 誤差関数 | 二乗誤差 平均二乗誤差 |
交差エントロピー | |
§ 二乗誤差の数式とpythonでの実装
$E_n(w)=\frac{1}{2}\displaystyle\sum^J_{j=1}(y_j-d_j)^2 ・・・ 平均二乗誤差$
下記コードは二乗誤差の実装部分
def mean_squared_error(d, y):
return np.mean(np.square(d -y)) / 2
◇ 確認テスト
○ ソフトマックス関数のソースコードの説明
$f(i,u)=\frac{e^{u_i}}{\sum^K_{k=1}e^{u_k}}の$
①$f(i,u)$
②$e^{u_i}$
③$\sum^K_{k=1}e^{u_k}$
①、②、③の部分を探すとともに各行の説明

○ 交差エントロピーのソースコードの説明
・ np.log(y[np.arange(batch_size),d] + 1e-7)にdを掛けていないのは
d=1であるからのように思う

実装演習(Section1~3)
1_1_forward_propagation ● 順伝播(単層・単ユニット) ・ 試してみようを試してみたが、relu関数のマイナスの値のテストが なかなかできなかったので、ウェイトを0、バイアスをマイナスにして テストしてみた→0が返ってくることを確認できた ● 順伝播(単層・複数ユニット)
・ コードを変えずに実行すると総入力が1より大きい値ばかりで
中間総出力は1に近い値ばかりだった
・ ウェイトを0にして実行すると、総入力が0に近い値になり
中間総出力は0.5に近い値ばかりとなった
・ W = np.random.randint(-5,0, size=(4,3)) でウェイトを増マイナスにすると
総入力がマイナスとなり、中間層出力では e-10が最後に付くような
小さな値ばかりとなった

● 順伝播(3層・複数ユニット)
・ 試してみようの「各パラメータのshapeを表示」と
「ネットワークの初期値ランダム生成」を行った

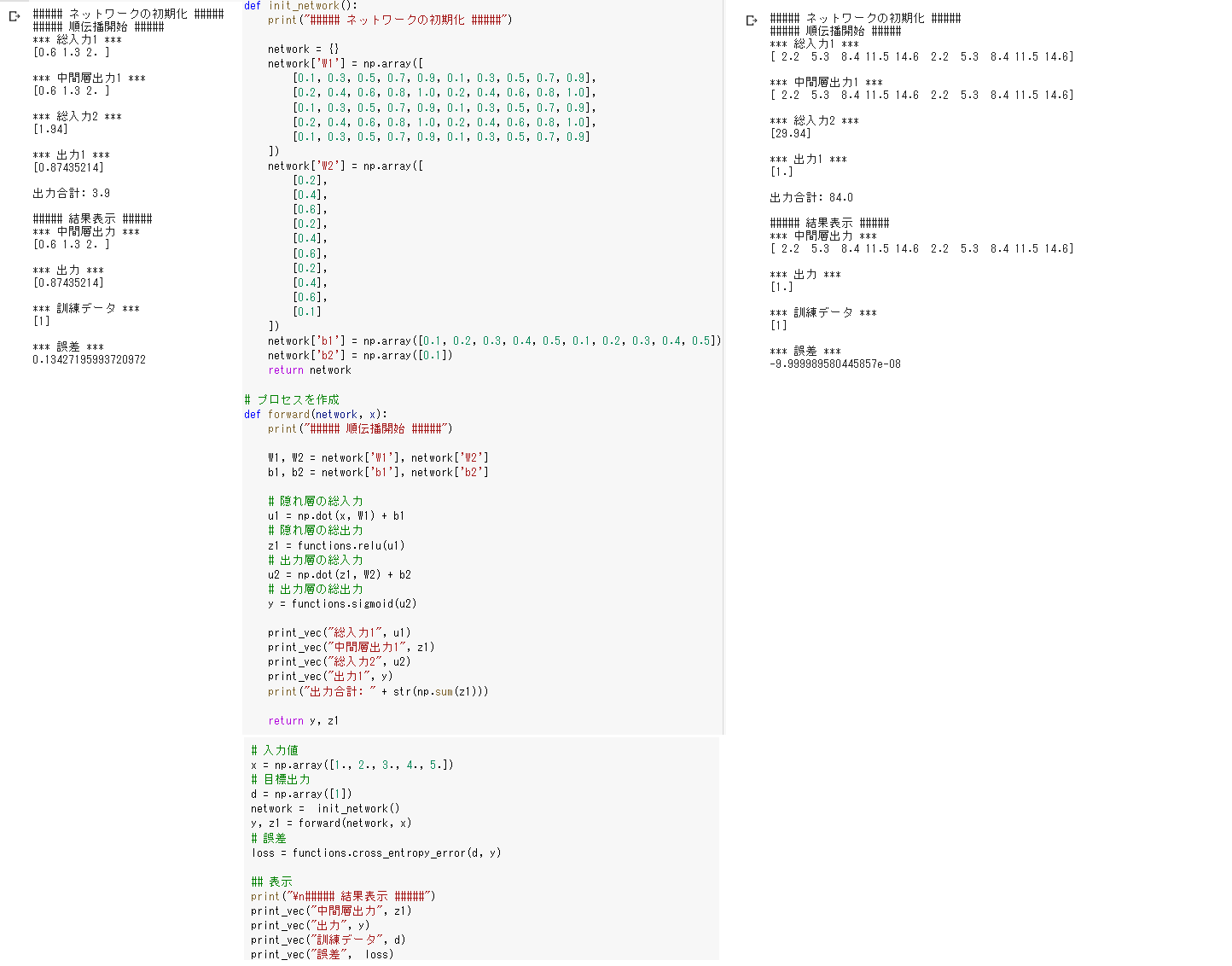
● 多クラス分類(2-3-4ネットワーク)
・ 左端はソースコードをそのまま実行した結果
真ん中は「ノードの構成を 3-5-4 に変更してみよう」で変更したソース
右端は真ん中のソースコード実行の結果
教師データがd = np.array([0, 0, 0, 1])だったのでわざとW2の1列目の値を大きく設定し
誤差が大きくなるようにして実行した結果、先ほどより大きな誤差が出力された
→ どの値に重きを置くかは重要である

● 回帰(2-3-2ネットワーク)
・ 左端はソースコードをそのまま実行した結果
真ん中は「ノードの構成を 3-5-4 に変更してみよう」で変更したソース
右端は真ん中のソースコード実行の結果
特に意図なく重み、バイアスを設定したが今回は誤差が小さくなった
重み、バイアスを操作すれば誤差はさらに小さくなると思う

● 2値分類(2-3-1ネットワーク)
・ 左端はソースコードをそのまま実行した結果
真ん中は「ノードの構成を 5-10-1 に変更してみよう」で変更したソース
右端は真ん中のソースコード実行の結果
出力層の活性化関数にシグモイド関数が使われているため
重み、バイアスを多少変化させても出力結果が変わらなかった
Section4:勾配降下法
§ 勾配降下法 深層学習は学習を通じて誤差を最小にするネットワークを作成すること ⇒ 誤差E(w)を最小化するパラメータwを発見すること ⇒ 勾配降下法を利用してパラメータwを最適化 $W^{(t+1)}=w^{t}-\epsilon\nabla E_n$ $\nabla E_n=\frac{\partial E}{\partial w}=\left[\frac{\partial E}{\partial w_1} ・・・\frac{\partial E}{\partial w_m}\right]$ $\epsilon:学習率$ ◇ 確認テスト ○ それぞれの式に該当するソースコードを探す ・$W^{(t+1)}=w^{t}-\epsilon\nabla E_n$ ⇒ network[key] -= learning_rate * grad[key] ・$\nabla E_n=\frac{\partial E}{\partial w}=\left[\frac{\partial E}{\partial w_1} ・・・\frac{\partial E}{\partial w_m}\right]$ ⇒ grad = backward(x, d, z1, y) ◆ 誤差の最小を勾配降下法によって求める
※ $\epsilon:学習率$
・ 学習率が大きすぎると最小値にたどり着かず発散してしまう
・ 学習率が小さすぎると収束するまでに時間がかかる
また底が沢山あるような式の場合、局所極小解(下図青い点の部分)で
学習が終わってしまう。本当に求めたいのは赤い点
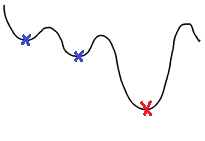
◆ 勾配降下法のアルゴリズム
● Momentum
● AdaGrad
● Adadelta
● Adam(よく使われる)
◆ エポック
● 入力データより求めた予測値と正解との誤差を誤差関数で計算し、その計算された
間違いの度合いをもとに重み(W)やバイアス(b)を更新し次の学習に反映する
この1サイクルをエポックと言う
● エポックは何回も繰り返す
◆ 確率的勾配降下法
$w^{t+1}=w^{(t)}-\epsilon\nabla E_n$
● 学習に使う全サンプルから一部分だけ使って学習を行う
サンプルが1000あるとした場合、1回目の学習ではランダムに選んだ
100のサンプルで学習し、次の学習ではまたランダムに選んだ
100のサンプルといった学習方法
(勾配降下法は全サンプルを一気に使って学習する)
● メリット
・ データが冗⻑な場合の計算コストの軽減
・ 望まない局所極小解に収束するリスクの軽減
・ オンライン学習ができるで
◇ 確認テスト
○ オンライン学習とは何か
データが来るたびに学習を行い、パラメータ(ウェイトとバイアス)を更新する
1回の学習あたりのコストが低く、はじめから全データを蓄えておかなくても良い
メモリの必要量が勾配降下法と比べて少なくて済む
◆ ミニバッチ勾配降下法
$w^{t+1}=w^{(t)}-\epsilon\nabla E_n$
$E_t=\frac{1}{N_t}\displaystyle\sum_{n\in D_t} E_n$ ※各ミニバッチの誤差を合計しミニバッチ数で割って
平均にしている
● オンライン学習の手法を勾配降下法(バッチ学習)で使えるようにした方法
全データを分割(ミニバッチ)し学習する
● メリット
・ 確率的勾配降下法のメリットを損なわず、計算機の計算資源を有効利用できる
→CPUを利用したスレッド並列化やGPUを利用したSIMD並列化
CPU自体の処理速度の向上は限界なので、たくさんのCPUで並行で処理して
速度を上げている
※SIMD:Single Instruction Multi Data
=1つの命令をたくさんのデータに対して同時実行する
◇ 確認テスト
○ 次の数式の意味を図に書いて説明せよ
$w^{(t+1)}=w^{(t)}-\epsilon \nabla E_n$

◆ 誤差勾配の計算
誤差勾配の計算に一般的な手法である数値微分を行うと
計算量が非常に大きくなるため誤差逆伝搬法を利用する
Section5:誤差逆伝搬法
§ 誤差逆伝搬法 算出された誤差を、出力層側から順に微分し、前の層前の層へと伝播。 最小限の計算で各パラメータでの微分値を解析的に計算する手法。 微分の連鎖率をうまく利用している。  ◇ 確認テスト
○ 誤差逆伝播法では不要な再帰的処理を避ける事が出来る。
既に行った計算結果を保持しているソースコードを抽出せよ。
赤枠の部分
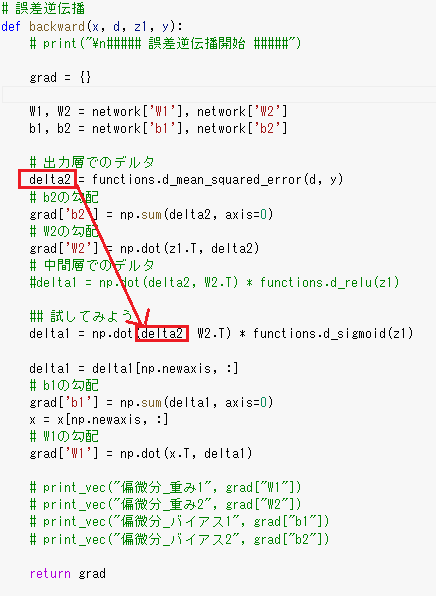
◆ 誤差勾配の計算

○ 最終的に以下のような式になる
$\frac{\partial E}{\partial y}\frac{\partial y}{\partial u}\frac{\partial u}{\partial w^{2}_{ji}}=(y-d)×1×\left[\begin{array}{l}0\\:\\z_i\\:\\0 \end{array}\right]=(y_j-d_j)z_j$
◇ 確認テスト
○ 2つの空欄に該当するソースコードを探せ
$\frac{\partial E}{\partial y}\frac{\partial y}{\partial u}$ delta2 = functions.d_mean_squared_error(d, y)
$\frac{\partial E}{\partial y}\frac{\partial y}{\partial u}\frac{\partial u}{\partial w_{ji}^{(2)}}$ grad['W2'] = np.dot(z1.T, delta2)
実装演習(Section4,5)
1_3_stochastic_gradient_descent ● 中間層の活性化関数をシグモイド関数で実行  ● 中間層の活性化関数をシグモイド関数→試してみようの # -5〜5のランダム数値 をテスト ・ 最初ワーニングが出たので(上段図) data_sets[i]['x'] = np.float128(np.random.rand(2) * 10 -5) と修正して再実行(中段図) ・ lossの合計が全く収束する兆しがないのでlossをprintで表示するとどんどん 大きくなっており勾配降下で発散してるのではないかと考え、 学習率を10分の1に下げてみたところ(下段図)収束の兆しが見られた。 ・ シグモイド関数はある値以下、または以上になると傾きがほぼ0になるので そうなると微分しても誤差をうまく逆伝播できないのではないか それであれば、値を大きくしてテストしたときにロスが収束しきらないことも 納得できる  ● 中間層の活性化関数をRELU関数で実行 ・ シグモイド関数版と比較すると収束が非常に速い(上段図) ・ 試してみようの # -5〜5のランダム数値 をテストするとオーバーフローを 起こしてしまった(中段図) 中段図の左上のところに1e210と表示されており、lossをprintで表示すると 値が大きすぎて計算できなくなっていた ・ シグモイド関数版と同じく学習率を10分の1に下げてみたところ(下段図) 収束するようになった → 学習率は非常に大事である 1_4_1_mnist_sample
● 先ほど得た教訓より学習率を調整してみる
・ 色々試してみた結果0.5当たりが精度がよさそうだった
もとの0.1や、大きくした値1.0の場合は最後の方まで振れが大きく、
最終的なテストデータでの正解率も学習率=0.5の場合のほうが良かった
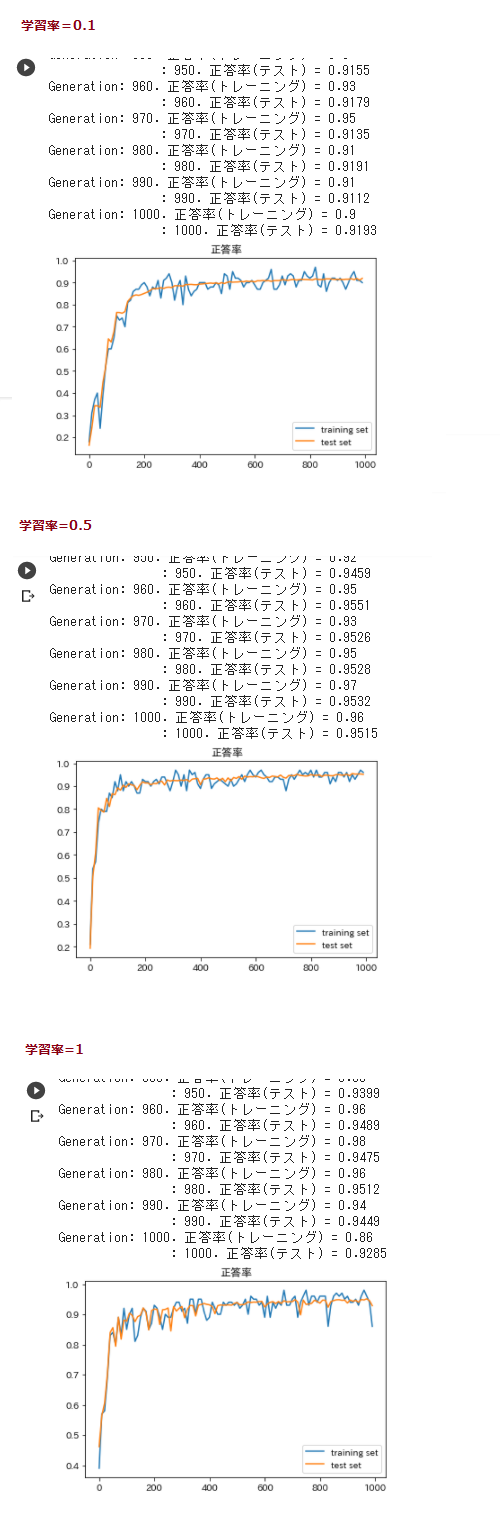
● 他の項目の値も変更してみた結果
・ 繰り返し数
4000くらいまでは正解率の精度が上がったが、それ以降はほとんど変わらなかった
・ 重み初期値補正係数
大きくすると早く正解率の精度が上がるが、大きくしすぎると最終的に振れが大きく
安定しにくかった。
小さくすると正解率の精度の上りが遅い。
0.3から0.5あたりがスピード、収束具合が良いように思った。
・ 中間層サイズ
値を変更しても正解率にあまり変化は見られなかった
・ ミニバッチサイズ
10にすると非常に正解率の精度が落ちた。300にすると正解率の精度は向上したが
時間がかかった。
・ Xavierの初期値、Heの初期値
試してみたが層が深くないせいかあまり影響は見られなかった
→ 学習率、重み、繰り返し数はそのデータに合うものがあり、
見つけ出す必要があるように思う。
ミニバッチサイズは大きいほうが精度は良くなるが、
時間とのトレードオフであるのと
コンピュータのスペックでの制限も受ける事を考えると
バランスであるように思う。
深層学習Day2
Section1:勾配消失問題
中間層を増やすと複雑な情報を上手く取り扱えるようにある → 中間層を増やすと勾配消失問題が起こる 誤差逆伝搬法は計算結果(=誤差)から微分を逆算するが 微分値が0~1の範囲のものが多いため層が多くなると勾配消失が起こる ◇ 確認テスト
○ 連鎖律の原理を使い、次式のdz/dxを求めよ
$z=t^2$
$t=x+y$
→ $\frac{\partial z}{\partial t}\frac{\partial t}{\partial x}$
→ $\frac{\partial z}{\partial t}=2t,\frac{\partial t}{\partial x}=1$
→ $\frac{d z}{dx}=2t×1=2t=2(x+y)$
§ 勾配消失問題
層が増えたときにが逆伝播で伝播される情報量が徐々に少なくなっていき
各重みが更新されなくなり、訓練が最適値に収束しなくなる
◆ 勾配消失が起きやすい活性化関数
● シグモイド関数
微分値が0~0.25範囲のため、中間層の活性化関数で何度も用いられると
連鎖率により微分値が掛け合わされて勾配が消失する
◇ 確認テスト
○ シグモイド関数を微分した時、入力値が0の時に最大値をとる。
その値として正しいものを選択肢から選べ
(2) 0.25
◆ 勾配消失の解決法
1.活性化関数の選択
シグモイド関数以外の活性化関数を選ぶ
● RELU関数
・ 今最も使われている活性化関数
・ 勾配消失問題の回避とスパース化に貢献することで良い成果を
もたらしている
・ 微分結果は0または1なので
1が伝わった重みは使われ、0が伝わった重みは使われない
2.重みの初期値設定
重みの決め方を工夫する
● Xavier
重みの要素を、前の層のノード数の平方根で除算した値を重みとする
(input_layer_size:前層のノード数)
np.random.randn(input_layer_size, hidden_layer_size) / np.sqrt(input_layer_size)
※ Xavierの初期値を設定する際の活性化関数
・ ReLU関数
・ シグモイド(ロジスティック)関数
・ 双曲線正接関数
● He
重みの要素を、前の層のノード数の平方根で除算した値に対し$\sqrt 2$を
かけ合わせた値
np.random.randn(input_layer_size, hidden_layer_size)
/ np.sqrt(input_layer_size) * np.sqrt(2)
※ Heの初期値を設定する際の活性化関数
・ ReLU関数
→ いずれの初期値設定もある程度の活性化関数の表現力を保ったまま
勾配消失への対策がとれる
◇ 確認テスト
○ 重みの初期値に0を設定すると、どのような問題が発生するか。
簡潔に説明せよ
⇒ 正しい学習が行えない。
重みに個性がなくなり、多数の重みを持つ意味がない。
3.バッチ正規化
● ミニバッチ単位で、入力値のデータの偏りを抑制する手法
● バッチ正規化の使い所
活性化関数に値を渡す前後に、バッチ正規化の処理を孕んだ層を加える
● バッチ正規化の数学的記述
$1.\mu_1=\frac{1}{N_t}\displaystyle\sum_{i=1}^{N_t}x_{ni} ・・・ ミニバッチ全体の平均$
$2.\sigma_t^2=\frac{1}{N_t}\displaystyle\sum_{i=1}^{N_t}(x_{ni}-\mu_t)^2 ・・・ ミニバッチの分散$
$3.\hat x_{ni}=\frac{(x_{ni}-\mu_t)}{\sqrt{\sigma_t^2+\theta}} ・・・ ミニバッチの正規化$
$4.y_{ni}=\gamma x_{ni}+\beta ・・・ 定数倍してバイアスを加算$
$N_i:ミニバッチのインデックス$
◇ 確認テスト
○ 一般的に考えられるバッチ正規化の効果を2点挙げよ
・ 学習を速く進行させられる
・ 初期値にそれほど依存しない
◇ 例題チャレンジ
答え:(1) data_x[i:i_end],data_t[i:i_end]
data_x,data_tともi番目からバッチサイズ分(i_end)のデータを取得する
Section2:学習率最適化手法について
$ 学習率最適化手法 ・初期の学習率を大きく設定し、徐々に学習率を小さくしていく ・パラメータ毎に学習率を可変させる 1.モメンタム
誤差をパラメータで微分したものと学習率の積を減算した後、
現在の重みに前回の重みを減算した値と慣性の積を加算する
● メリット
・ 局所的最適解にはならず、大域的最適解となる
・ 谷間についてから最も低い位置(最適値)にいくまでの時間が早い
● 数式とコード
$V_t=\mu V_{t-1}-\epsilon\nabla E$
self.v[key] = self.momentum* self.v[key] -self.learning_rate* grad[key]
$w^{(t+1)}=w^{t}+V_t$
params[key] += self.v[key]
$慣性:\mu (ハイパーパラメータ)$
※ 前回の重みも用いて学習を進めていく
進みが良い方向に一気に進む
2.AdaGrad
誤差をパラメータで微分したものと再定義した学習率の積を減算する
● メリット
・ 勾配の緩やかな斜面に対して、最適値に近づける
● 課題
・ 学習率が徐々に小さくなるので、鞍点問題を引き起こす事があった
→RMSPropへ
● 数式とコード
$h_0=\theta ()$
self.h[key] = np.zeros_like(val)
$h_t=h_{t-1}+(\nabla E)^2$
self.h[key] += grad[key] * grad[key]
$w^{(t+1)}=w^{(t)}-\epsilon\frac{1}{\sqrt{h_t}+\theta}\nabla E$
params[key] -= self.learning_rate* grad[key] / (np.sqrt(self.h[key]) + 1e-7)
※ 過去の学習率も活かして学習を進めていく
3.RMSProp
誤差をパラメータで微分したものと再定義した学習率の積を減算する
AdaGradの改良版
● メリット
・ 局所的最適解にはならず、大域的最適解となる
・ ハイパーパラメータの調整が必要な場合が少ない
● 数式とコード
$h_t=\alpha h_{t-1}+(1-\alpha)(\nabla E)^2$
self.h[key] *= self.decay_rate
self.h[key] += (1 -self.decay_rate) * grad[key] * grad[key]
$w^{(t+1)}=w^{(t)}-\epsilon\frac{1}{\sqrt{h_t}+\theta}\nabla E$
params[key] -= self.learning_rate* grad[key] / (np.sqrt(self.h[key]) + 1e-7)
※ $\alpha$によって、どれくらい前回の経験を活かすか、
どれくらい今回の経験を生かすかを決められる
過去の学習率も活かして学習を進めていく
4.Adam
モメンタムの、過去の勾配の指数関数的減衰平均と
RMSPropの、過去の勾配の2乗の指数関数的減衰平均を
それぞれ孕んだ最適化アルゴリズム
今一番用いられている最適化手法
● メリット
モメンタムおよびRMSPropのメリットを孕んだアルゴリズム
◇ 確認テスト
○ モメンタム・AdaGrad・RMSPropの特徴をそれぞれ簡潔に説明せよ
・ モメンタム:前回の更新量を利用して慣性項を追加する
・ AdaGrad:勾配の緩やかな斜面に対して、最適値に近づけるが
鞍点問題を引き起こす事がある
・ RMSProp:AdaGradを改善した手法で、
更新量が小さくなり過ぎて鞍点問題を引き起こさないようにしている
Section3:過学習について
§ 過学習 ・ テスト誤差と訓練誤差とで学習曲線が乖離すること ・ 特定の訓練サンプルに対して、特化して学習する ※ 下図の右側が過学習  ● 原因 ・ 入力値に対して、パラメータ数やノードが多い ・ パラメータの値が適切でない などにより ネットワークの自由度が高く(ニューラルネットワークが複雑な表現が可能に) なり、特定の訓練サンプルに対して、特化して学習してしまう ◇ 確認テスト
機械学習で使われる線形モデルの正則化は、
モデルの重みを制限することで可能になる
前述の線形モデルの正則化手法の中にリッジ回帰という手法があり
その特徴として正しいものを選択しなさい
⇒ (a)ハイパーパラメータを大きな値に設定すると、
すべての重みが限りなく0に近づく
● 実際にニューラルネットワークの中でどのようなことが起きているか
重みが極端に大きい値になっていることがある
⇒ 学習させていくと、重みにばらつきが発生する
重みが大きい値は、学習において重要な値であり
重みが大きいと過学習が起こる
● 過学習の解決策
誤差に対して、正則化項を加算することで、重みを抑制する
⇒ 過学習がおこりそうな重みの大きさ以下で重みをコントロールし
かつ重みの大きさにばらつきを出す必要がある
● L1正則化、L2正則化(リッジ回帰)
$E_n(w)+\frac{1}{p}\lambda||x||p$ 誤差関数にpノルムを加える ($\lambda$はハイパーパラメータ)
$||x||p=(|x_1|^p+…+|x_n|^p)^{\frac{1}{p}}$ pノルムの計算
ノルム=距離
p=1の場合、L1正則化(ラッソ回帰)
p=2の場合、L2正則化(リッジ回帰)
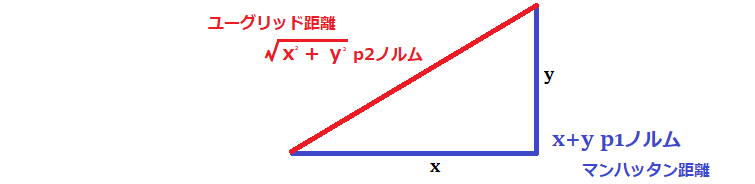
・ 正則化の計算
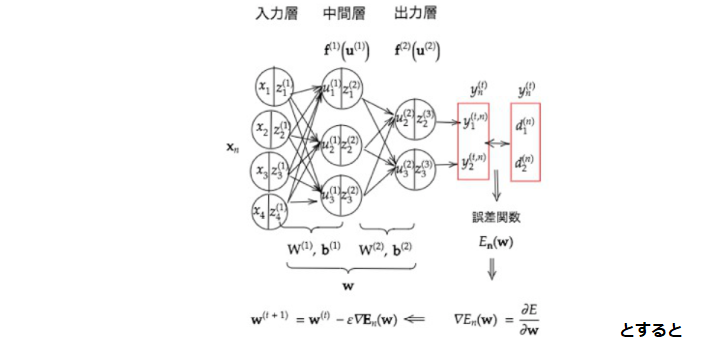
$||w^{(1)}||_p=(|w_1^{(1)}|^p+…+|w_n^{(1)}|^p)^{\frac{1}{p}}$
$||w^{(2)}||_p=(|w_1^{(2)}|^p+…+|w_n^{(2)}|^p)^{\frac{1}{p}}$
$||x||_p=||w_1||_p+||w_2||_p$
$E_n(w)+\frac{1}{p}\lambda||x||_p$
・ 数式とコード
$||x||p=(|x_1|^p+…+|x_n|^p)^{\frac{1}{p}}$
L1:np.sum(np.abs(network.params['W' + str(idx)]))
L2:np.sqrt(np.sum(network.params['W' + str(idx)] ** 2))
$E_n(w)+\frac{1}{p}\lambda||x||p$
L1:weight_decay+=
weight_decay_lambda*np.sum(np.abs(network.params['W' + str(idx)]))
loss = network.loss(x_batch, d_batch) + weight_decay
L2:weight_decay += 0.5 * weight_decay_lambda
* np.sqrt(np.sum(network.params['W' + str(idx)] ** 2))
◇ 確認テスト
下図についてL1正則化を表しているグラフはどちらか
⇒ 右側
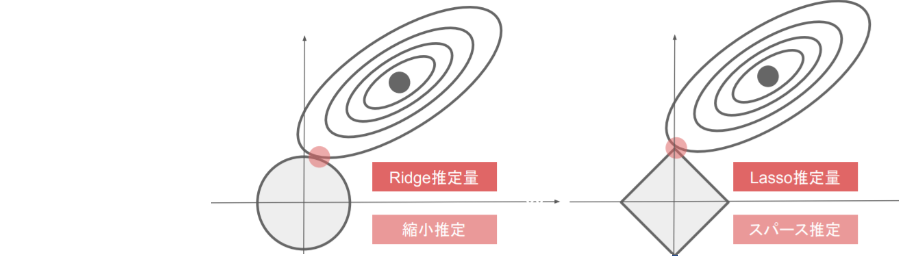
◇ 例題チャレンジ
○ 5.L2パラメータ正則化
⇒ (4) param
勾配を求めるときに微分するためparam$^2$が微分されて2paramとなる
(2は係数なのでrateに吸収されていると考える)
○ 6.L1パラメータ正則化
⇒ (3) np.sign(param)
○ 7.データ集合の拡張
⇒ (4) image[top:bottom, left:right, :]
● ドロップアウト
ノードの数が多い場合にランダムにノードを削除して学習させる
・ メリット
データ量を変化させずに、異なるモデルを学習させていると解釈できる
シンプルであるが効果が高い
Section4:畳み込みニューラルネットワークの概念
§ 畳み込みニューラルネットワーク(CNN) ・ 画像処理でよく用いられる ・ 汎用性が高く次元間でつながりのあるデータを扱える CNNの構造図(例) 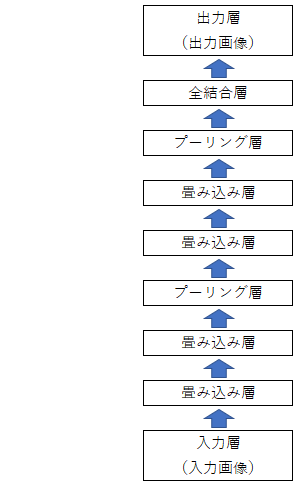 CNNで扱えるデータの例| 1次元 | 2次元 | 3次元 | |
| 単一チャンネル | 音声 次元:時刻 チャンネル:強度 |
フーリエ変換した音声 次元:時刻,周波数 チャンネル:強度 |
CTスキャン画像 次元:x,y,z チャンネル:強度 |
| 複数チャンネル | アニメのスケルトン 次元:時刻 チャンネル:腕の値,膝の値… |
次元:x,y チャンネル:R,G,B |
動画 次元:時刻,x,y チャンネル:R,G,B |
CNNの原型であるLeNetの構造
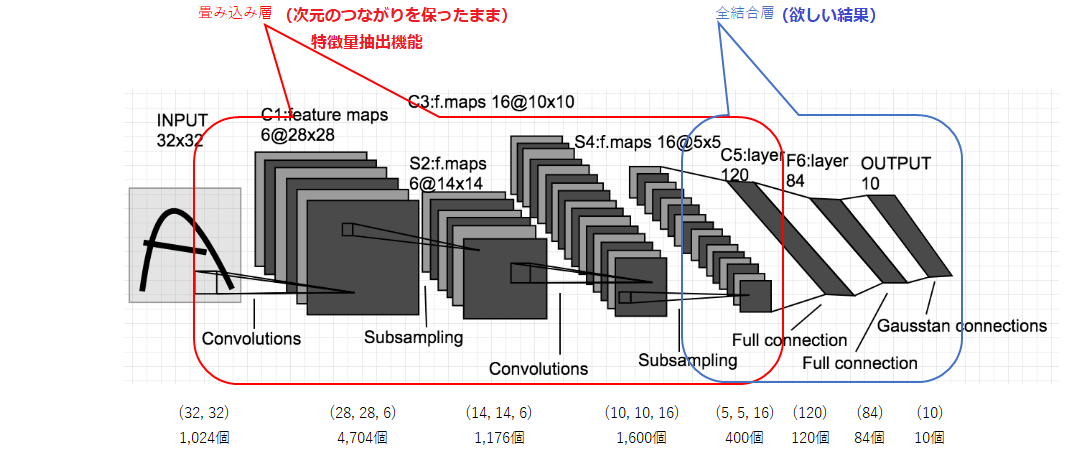
◆ 畳み込み層
● 畳み込み層の全体像
※ 周りの情報とのつながりを保ったまま情報を処理している
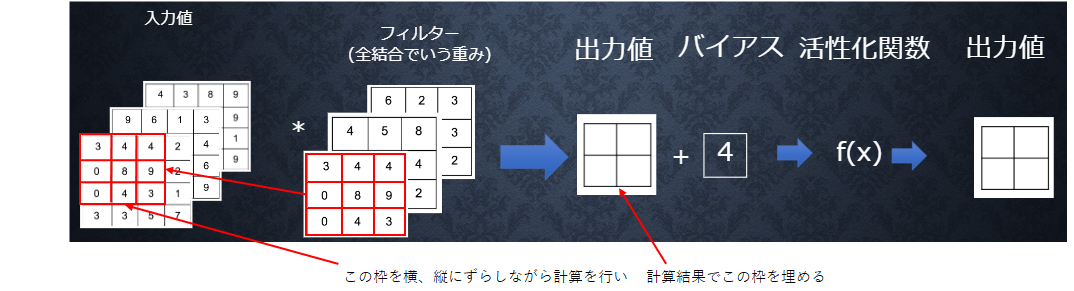
・ 畳み込み層では、画像の場合、縦、横、チャンネルの3次元のデータを
そのまま学習し、次に伝えることができる。
⇒ 3次元の空間情報も学習できるような層が畳み込み層である。
● 畳み込み層の演算
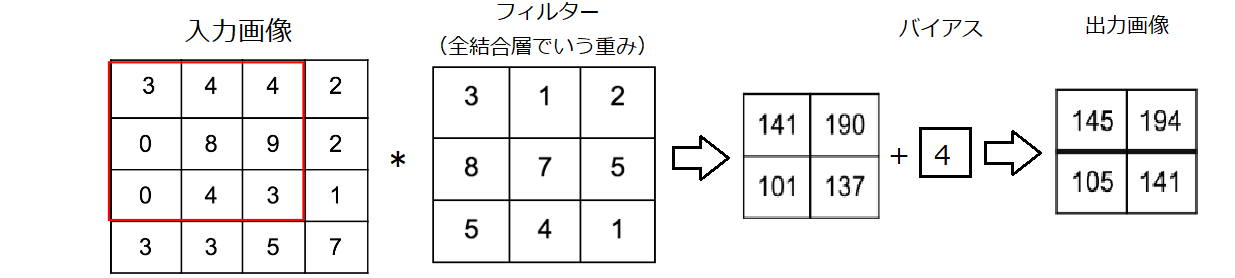
3×3 + 4×1 + 4×2 + 0×8 + 8×7 + 9×5 + 0×5 + 4×4 + 3×1 = 141
4×3 + 4×1 + 2×2 + 8×8 + 9×7 + 2×5 + 4×5 + 3×4 + 1×1 = 190
0×3 + 8×1 + 9×2 + 0×8 + 4×7 + 3×5 + 3×5 + 3×4 + 5×1 = 101
8×3 + 9×1 + 2×2 + 4×8 + 3×7 + 1×5 + 3×5 + 5×4 + 7×1 = 137
● パディング
畳み込み層の演算で見たようにフィルターを通すと出力画像が小さくなる
⇒ 出力画像が小さくならないようにするにはパディングを行う
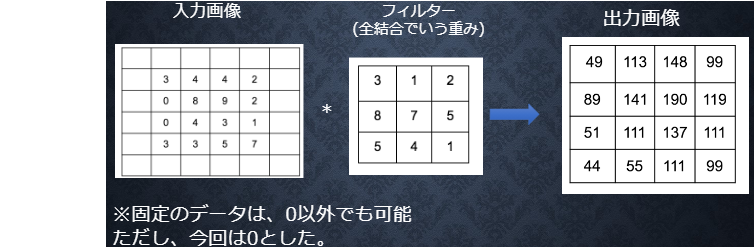
● ストライド
フィルターを横、縦に移動させる際の移動させる枠の個数
ストライドを大きくすると、出力画像は小さくなる
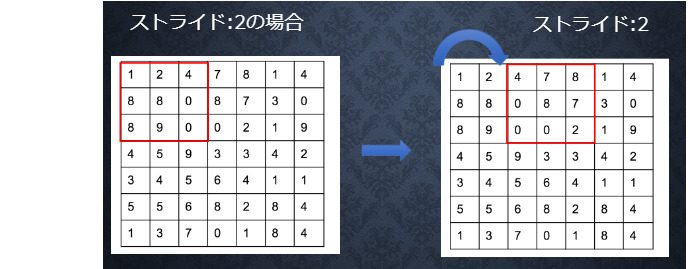
● チャンネル
フィルターの数=チャンネルの数
● 全結合で画像を学習した際の課題
画像の場合、縦、横、チャンネルの3次元データだが、1次元のデータとして処理される
⇒ RGBの各チャンネル間の関連性が、学習に反映されない
畳み込み層を使って学習すれば縦、横、チャンネルの関連性を保ったまま学習できる
◆ プーリング層
MAXプーリング、アベレージプーリングなどがある
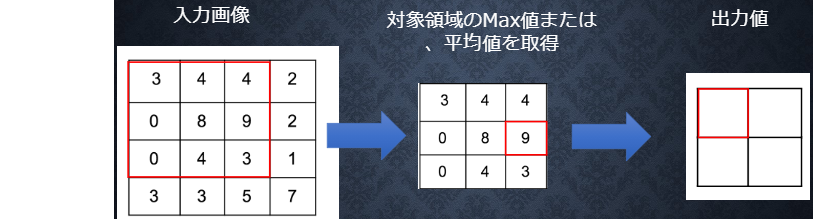
上記の場合、MAXプーリングなら
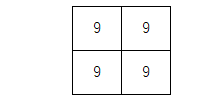
アベレージプーリングなら
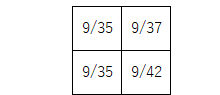
が出力値となる
◇確認テスト
サイズ6×6の入力画像を、サイズ2×2のフィルタで畳み込んだ時の出力画像の
サイズを答えよ。なおストライドとパディングは1とする
○ 公式
$O_H=\frac{画像の高さ+2×パディング高-フィルター高さ}{ストライド}+1$
$O_W=\frac{画像の幅+2×パディング幅-フィルター幅}{ストライド}+1$
公式に当てはめると
$O_H=\frac{6 + 2 × 1 - 2}{1}+1 = 7$
$O_W=\frac{6 + 2 × 1 - 2}{1}+1 = 7$
よって 出力画像は7×7のサイズ
Section5:最新のCNN
◆ AlexNetのモデル 過学習を防ぐ施策 ・ サイズ4096の全結合層の出力にドロップアウトを使用している 実装演習(Section1~5)
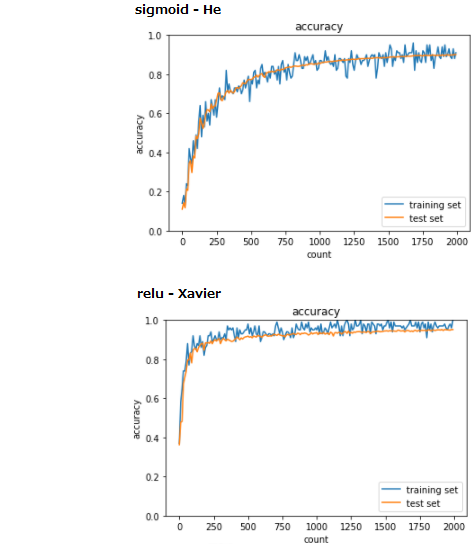
2_1_network_modified ● 1_4_1_mnist_sampleをOrderedDictを用いた形にしているものを実行 ・ 重み初期値補正係数、繰り返し数、ミニバッチサイズ、学習率が同じであるからか 結果は1_4_1のときとあまり変わらなかった ・ class Relu、class Affineは使用されていないようだった  2_2_1_vanishing_gradient ● 勾配消失について4つのパターンを実行 ・ 活性化関数にsigmoid、重みの初期値に正規分布を用いた「sigmoid - gauss」は 全く学習が進まなかった ・ 活性化関数にRelu、重みの初期値に正規分布を用いた「Relu - gauss」は 500回目あたりから急に学習が進んだ ・ 活性化関数にsigmoid、重みの初期値にXavierを用いた「sigmoid- Xavier」は 「sigmoid - gauss」のときよりも学習がすすんだものの、まだ正答率があがるのでは ないかと思い、繰り返し=5000回、10000回も試してみた 5000回の場合は2000回のときよりも正答率は0.07程度上がったが 5000回と10000回ではほとんど変わらない正答率だった ・ 活性化関数にRelu、重みの初期値にHeを用いた「Relu - He」は 4パターンの中で最も学習も早く正答率も高かった → 理論的にも「sigmoid - gauss」が勾配消失を起こすことは知られているので この手法は避けるべきなのははっきりしているが、ここで試した残りの3パターンは 今回においては「Relu - He」が優秀であったが、 常にそうであるのかは気になることろである。  2_2_2_vanishing_gradient_modified ● 「2_2_1_vanishing_gradient」の共通部分をクラスにまとめた 「2_2_2_vanishing_gradient_modified」の[try] を試してみた (1) hidden_size_listの数字を変更してみよう ・ 「sigmoid - gauss」はhidden_size_listの値を増やしても減らしても まったく学習が進まなかった ・ 「ReLU - gauss」はhidden_size_listの値を増やしても学習のスピードや正答率は ほとんど変わらなかったが、減らすと学習スピードが落ち、 先ほどと同じ2000回の学習では明らかに正答率が悪くなった ・ 「sigmoid - Xavier」はhidden_size_listの値を増やすと学習速度が上がり 正答率も高くなった。減らすと学習スピードは若干落ちたように思うが、 先ほどと同じ2000回の学習では正答率は少し良くなった ただし、hidden_size_listの値を極端に減らすと正答率は悪くなった ・ 「ReLU - He」はhidden_size_listの値を増やすと、途中から トレーニングデータの正答率とテストデータの正答率に 若干差が生まれた。hidden_size_listの値を減らすと学習スピードが落ち、 先ほどと同じ2000回の学習での正答率は低くなった → 隠れ層のノード数はそれぞれに適した数があるように思った。 ここではデータは同じなので、活性化関数や重みの初期値に関連していると 思われる。 (2) sigmoid - He と relu - Xavier についても試してみよう
・ sigmoid関数はXavierを使用した方が良いとされているが、
ここではHeを使用したときの方が正答率が良くなった
このデータは偶然そうなったのか?
色々なデータで試してみないと理由についてはここでは何とも言えない。
・ relu 関数についてはXavierを使用してもHe を使用してもあまり変わらなかった
2_3_batch_normalization
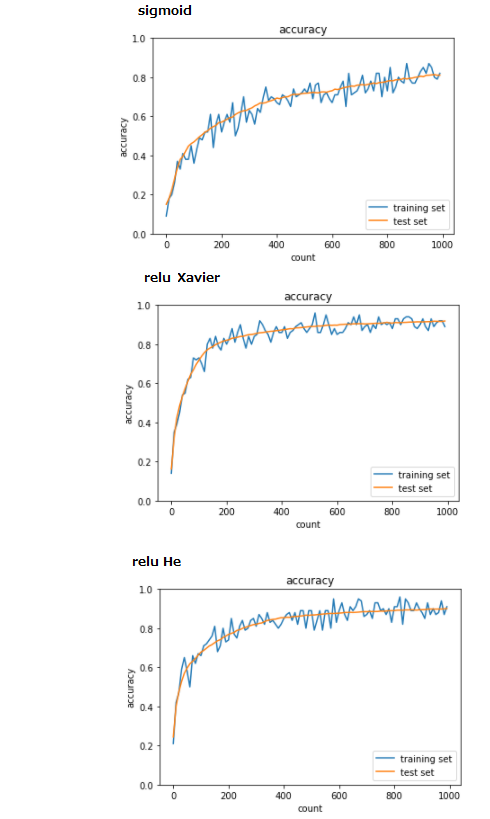
● 「[try] 活性化関数や重みの初期値を変えてみよう」を行った
・ 重みの初期値よりも活性化関数の影響の方が大きい
・ バッチ正則化 layerはここでは使用されていないようだった
2_4_optimizer
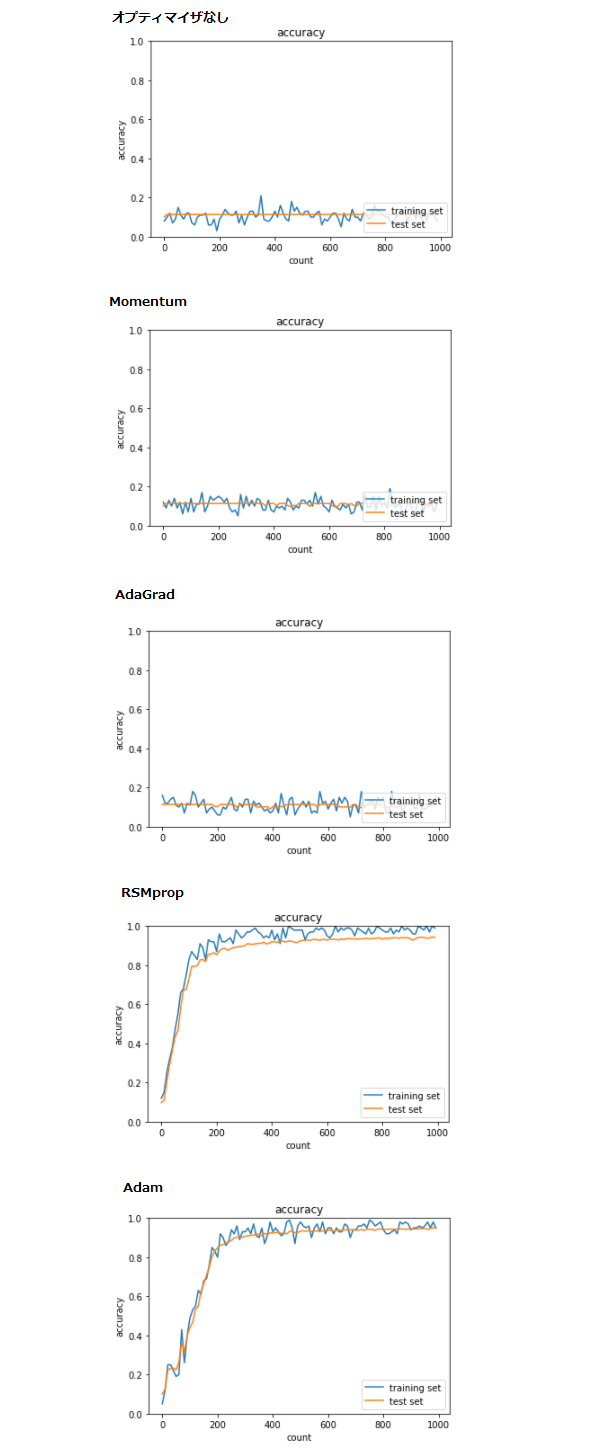
● 全オプティマイザのソースを実行した
・ RSMprop、Adam以外は学習に失敗した
・ RSMpropとAdamを比較するとAdamの方が最終的な正答率が高い
● [try] 学習率を変えてみよう
・ Adamを使用したソースで試してみた
学習率を大きくすると最終的な正答率が悪くなった
学習率を小さくすると学習速度は落ちるが最終的な正答率は変わらなかった
最初に設定されている学習率=0.01は適切であったのではないだろうか
● [try] 活性化関数と重みの初期化方法を変えてみよう
● [try] バッチ正規化をしてみよう
・ Adamを使用したソースで試してみた
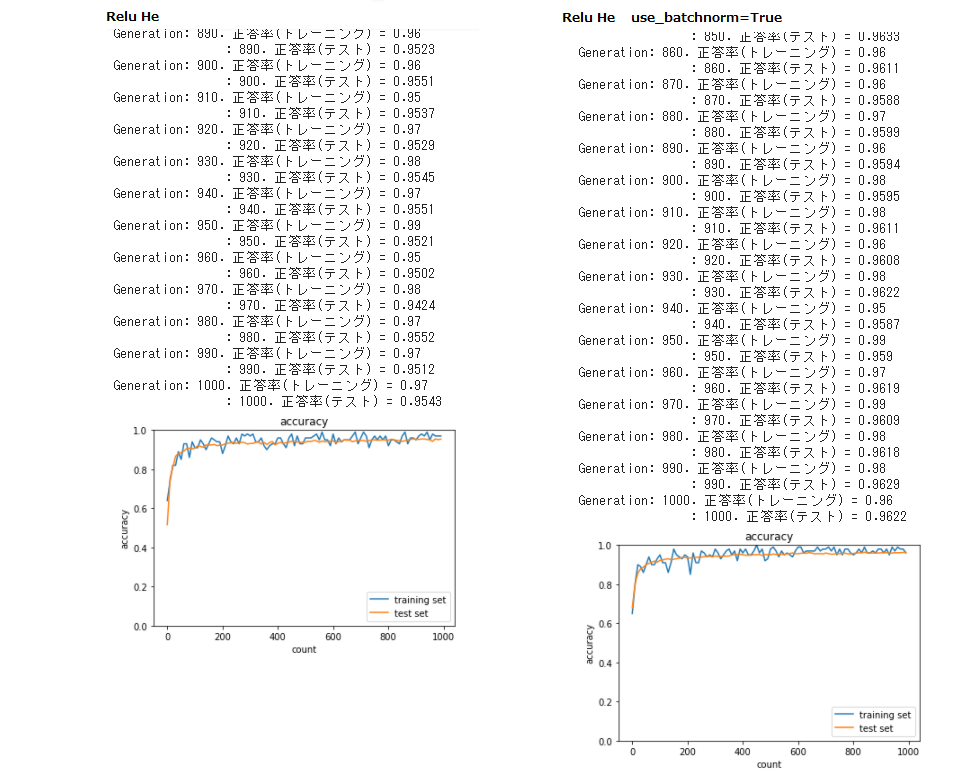
活性化関数=Relu、重みの初期化方法=Heにすると学習スピードが非常に早くなった
正答率も少し良くなった
さらにバッチ正規化を行うと学習スピードは先ほどとあまり変わらないが
正答率が若干良くなった
→ 活性化関数はRelu、オプティマイザはAdamを使用するのが良く
重みの初期値はXavier、Heのいずれか(試してみて結果の良い方)
またバッチ正規化は行った方が良い結果が期待できると思う。
2_5_overfiting
● 全てのソースを実行した
・ 過学習の対策の無いものから、何らかの過学習対策をしたソースを実行したが
どれも過学習を完全に防げていない
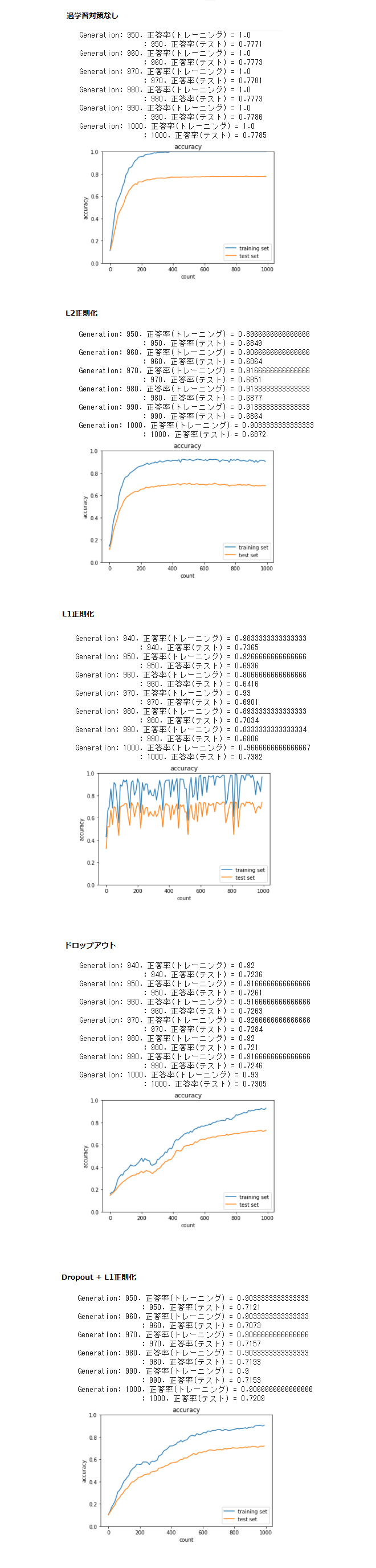
● [try] weigth_decay_lambdaの値を変更して正則化の強さを確認しよう
・ L2正則化のweigth_decay_lambdaの値を大きくすると、学習が失敗するようになった
小さくすると過学習が防げず、いずれの場合も学習がうまくいかなかった。
・ L1正則化においてもweigth_decay_lambdaの値を大きくすると、
学習が失敗するようになった
小さくすると過学習が防げず、いずれの場合も学習がうまくいかなかった。
● [try] dropout_ratioの値を変更してみよう
・ dropout_ratioの値を大きくすると、学習がうまくいかない(正答率が上がらない)
小さくすると過学習が防げず、いずれの場合も学習がうまくいかなかった。
● [try] optimizerとdropout_ratioの値を変更してみよう
・ optimizerにAdamを使うと学習速度が上がり、dropout_ratioの値を大きくしても
学習に失敗しにくくはなった。ただ過学習は防げなかった。
→ 正則化やドロップアウトを用いても、データ数が少ないと過学習が起こりやすい
2_6_simple_convolution_network_after
● 既存のソースコードのまま実行した
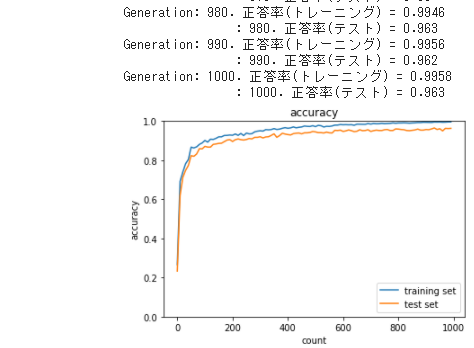
● [try] im2colの処理を確認しよう
・ どのように変換されているかを確認した
これはこの後の実際の処理では「layers.Convolution.forward()」で
同じような変換が行われていた
また、[try] col2imの処理を確認しようではこれと逆の変換が行われている
こちらは「layers.Convolution.backward()」で同じような変換が行われていた

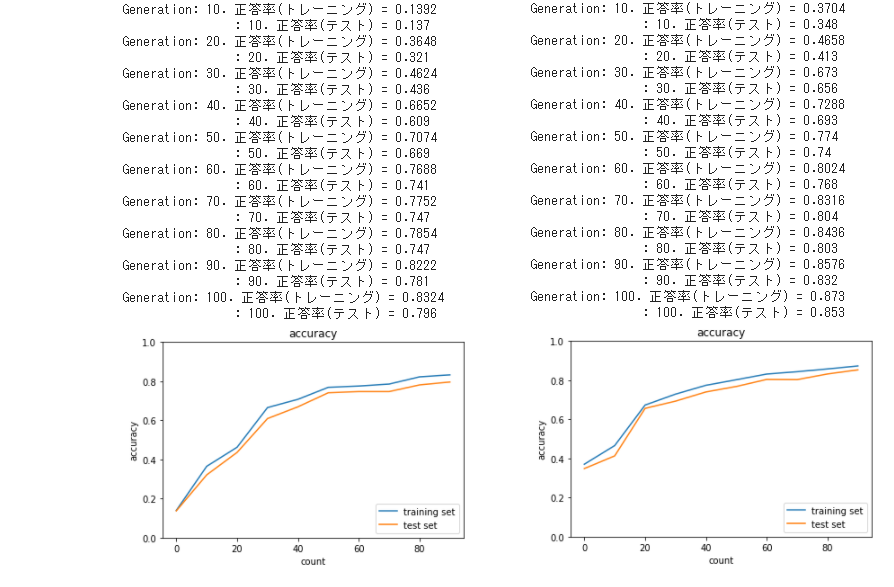
2_7_double_comvolution_network(左)
2_7_double_comvolution_network_after(右)
● プーリング層を減らした右側の方が結果が良くなっている。
プーリング層で情報が落ちてしまうのだろうか
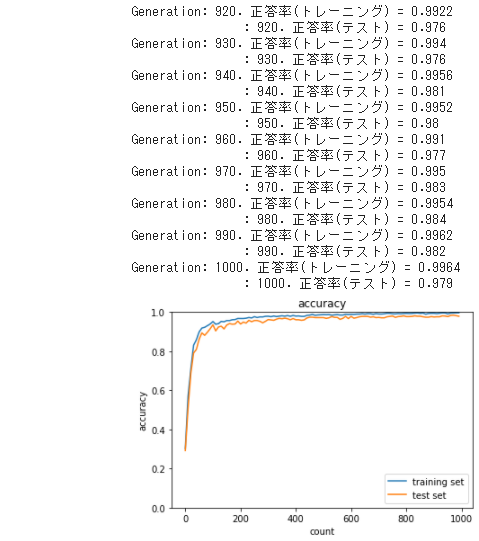
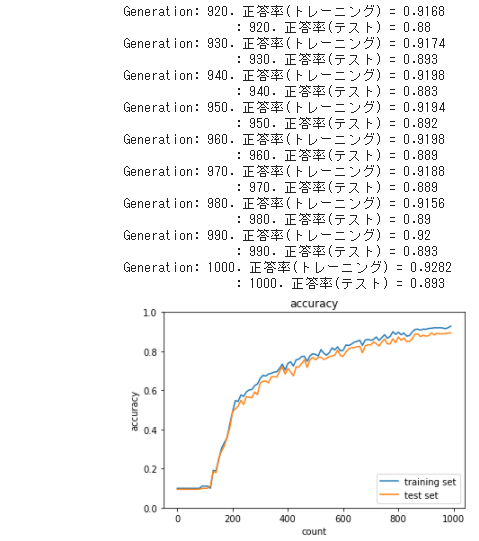
2_8_deep_convolution_net
● 既存のソースコードのまま実行した
● 重みの初期化にHeを用いず「2_6_simple_convolution_network_after」のように
ランダムな値に一律で0.01をかけてテストしてみた
・ 先ほどと全く違った結果となり、学習が遅く
同じ1000回の学習回数での正答率も悪くなった。
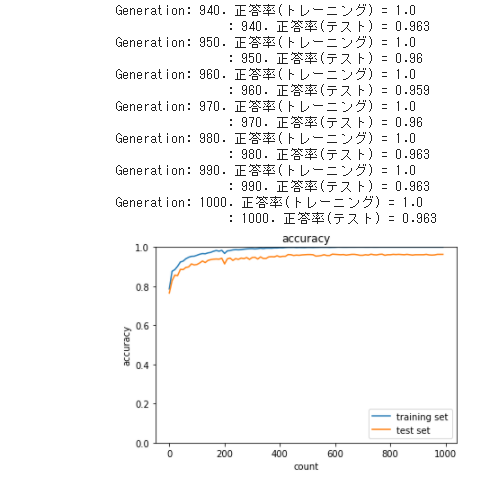
● 「2_6_simple_convolution_network_after」に重みの初期化Heを用いてテストしてみた
・ 最終的な正答率は変わらないが、最初から正答率が高くなった
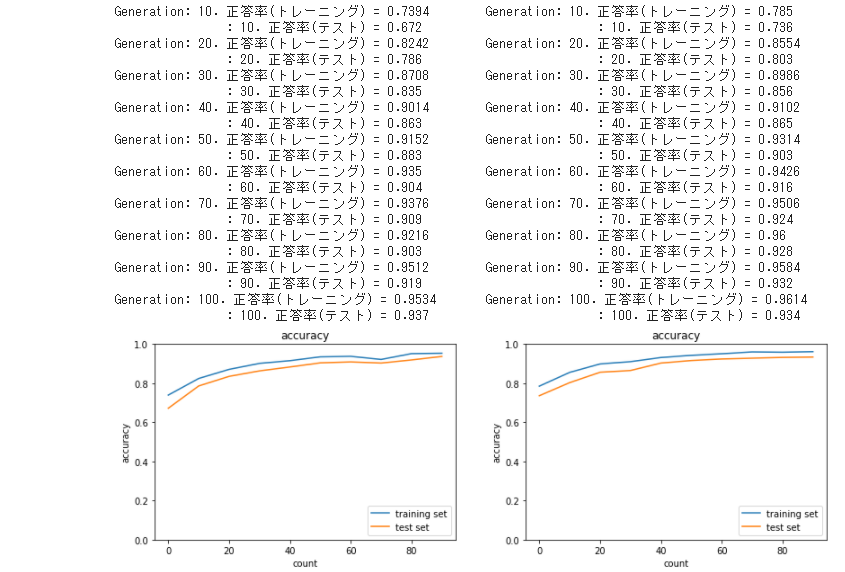
● 「2_7_double_comvolution_network」と「2_7_double_comvolution_network_after」に
重みの初期化Heを用いてテストしてみた
2_7_double_comvolution_network(左)
2_7_double_comvolution_network_after(右)
・ この2つは先程も比較したが、今回は大きな差は見られなかった
→ 層を増やすことも正答率を上げるのに効果がありそうだが
勾配を消失させないこと、重みにそれぞれ個性があることも重要であるように思った