・ 自分で関数（式）を作る
・ 極座標と直交座標
・ ベルヌーイのスケート曲線
ベルヌーイのスケート曲線
スケート曲線の式は、こんな感じです どんな風かはすぐには想像できないですが、
下のwikipediaのサイトにある動画では、こんな風に双曲線を元に図式化してあります
双曲線の接線（青い太い線）に、原点から接線（赤い太い線）をおろしていき、交差した点がスケート曲線（細い赤い線）になるようです 原点と青い太い線の距離が最も短くなる点ということですね
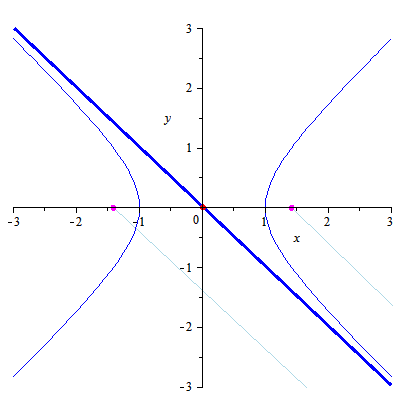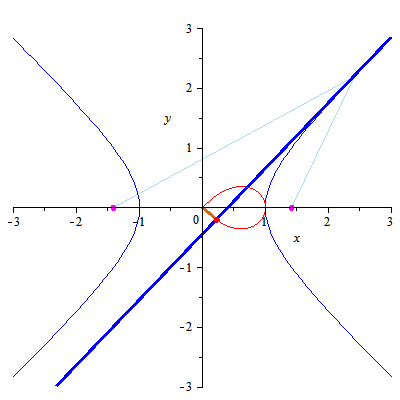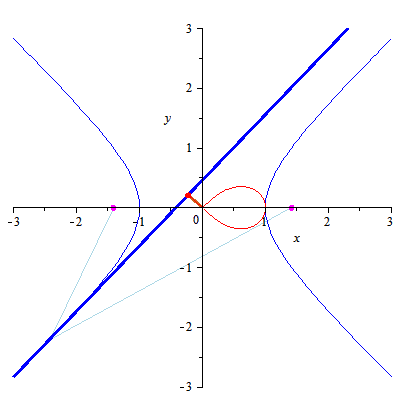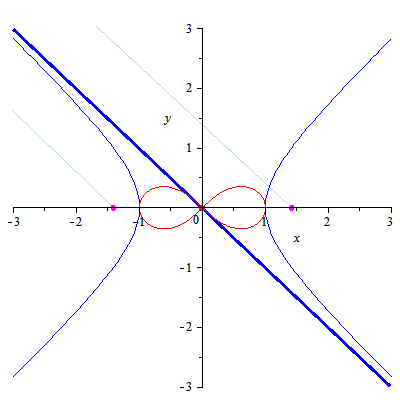
ベルヌーイのスケート曲線についてはリンクの説明をお読みください
・ Lemniscate_of_Bernoulli (English)
名前の由来
数学者のヤコブ・ベルヌーイさんの名前がついています ヤコブ・ベルヌーイさんとヨハン・ベルヌーイさんは、兄弟で有名な数学者だそうですが、ベルヌーイさんの家系は、ベルヌーイ試行とベルヌーイ数、ベルヌーイの法則など、たくさんあって何かの時に聞いたことがありますね
描画
さあ、描いてみましょう 手元にMATLABがあるので、それを使ってプロットしています コードは図の後に付けてます 角度（theta）なので t を使って作ります
bernoulli
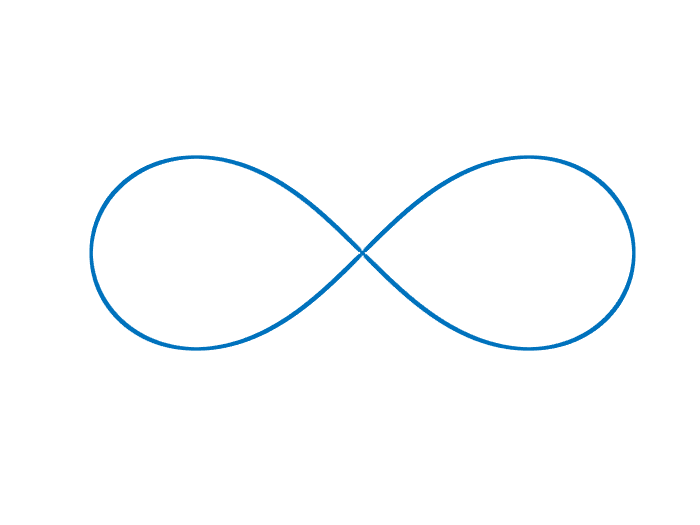
clear;
t = 0:.0001:pi * 2;
r = @(t) sqrt(cos(2*t) ) ;
figure;
plot(r(t).*cos(t), r(t).*sin(t), '.');
axis equal;
axis off;
少し変形して花のバリエーションを作ってみました
「スケート曲線」なので、ほんとは角度を狭めて ∞ （無限のマーク）のとこだけ描くものなのかもしれませんが、360° ( 2 × π )にしたら四葉のクローバー型になりました
original
clear;
t = 0:.0001:pi * 2;
func = @(t) sqrt(cos(2*t) ) ;
rsqared = func(t);
r = sqrt(rsqared);
figure;
plot(r.*cos(t), r.*sin(t), '.');
axis equal;
axis off;
abs（absolute）をひとつ入れると花弁が同じ大きさに
なお、デフォルトで、sqrtから先の計算には複素数の変数が使われてます
version2
clear;
t = 0:.0001:pi * 2;
func = @(t) sqrt(cos(2*t) ) ;
rsqared = func(t);
r = sqrt(abs(rsqared));
figure;
plot(r.*cos(t), r.*sin(t), '.');
axis equal;
axis off;
45° 回転した場合 cos => sin に変えるとこんな風に回転します
rotated
clear;
t = 0:.0001:pi * 2;
func = @(t) sqrt(sin(2*t) ) ;
rsqared = func(t);
r = sqrt(rsqared);
figure;
plot(r.*cos(t), r.*sin(t), '.');
axis equal;
axis off;
originalをもとに、菊の花にしてみました（季節柄）
chrysanthemum
clear;
t = 0:.0001:pi * 8;
func = @(t) sqrt(cos(2*t) ) ;
rsqared = func(t);
r = sqrt(rsqared);
figure;
plot(r.*cos(t/4), r.*sin(t/4), '.');
axis equal;
axis off;
クリスマスまでには、これを利用して立体のモミの木を作ってみる予定です