Power Automate で 整列！

序：基礎研究って大事

なんでしょう、急に数列を作りたくなることってありますよね。

冗談はさておき、ブラウザに「Power Automate 数列」と入力してネット上を検索してみたものの、自分の探した範囲では、まだ Power Automate（クラウドフロー）で数列について触れている記事はなさそうでした。

現在の筆者は、何か技術の記事を書く時、上に引いたような「一つの記事や資料が、さらに複数のアウトプットへと発展するような理想的なドキュメント」を心がけるようにしています。

もちろん、忙しい市民開発者の皆さまがすぐにコピペで活用できる技術ブログにも大きな価値があり、その利便性を否定するつもりはありません。かくいう筆者も幾度となく助けられたことがあります。しかし、今回は、ふらりさんへのリスペクトを込めて、あくまで「開発の起点」としての土台作りに焦点を当て、Power Automate を使った数列の生成方法をご紹介します。

本音を漏らせば、現時点で業務への応用ポイントとしてすぐ思い付くのは「偶数列と奇数列」くらいかもしれません。とはいえ「基礎研究」とは、役に立つか否かを二元論で語るものではありません。

何が将来のアイディアを生むかは予測困難です。一見、何の意味もなさそうな研究が誰かの目に留まったことによって、偉大な研究が生まれた事例は数多く存在します。本記事が、皆さまの日々の自動化設計や応用シナリオにおいて、新たな発想のきっかけになれば幸いです。

等差数列

等差数列とは、隣り合う項同士の差（公差）が一定になる数列のことです。次の例を見てみましょう。

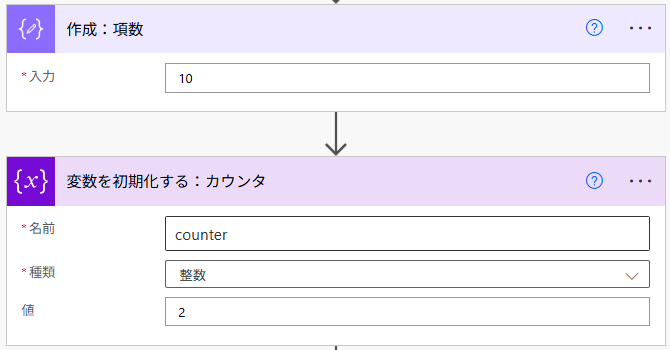
• 項数：10
• 初項：1
• 公差：3

この場合の等差数列は、1, 4, 7, 10, 13, 16, 19, 22, 25, 28 です。初項 1 から 公差 3 ずつ、一定に増えていることがわかります。これを Power Automate で実装してみます。

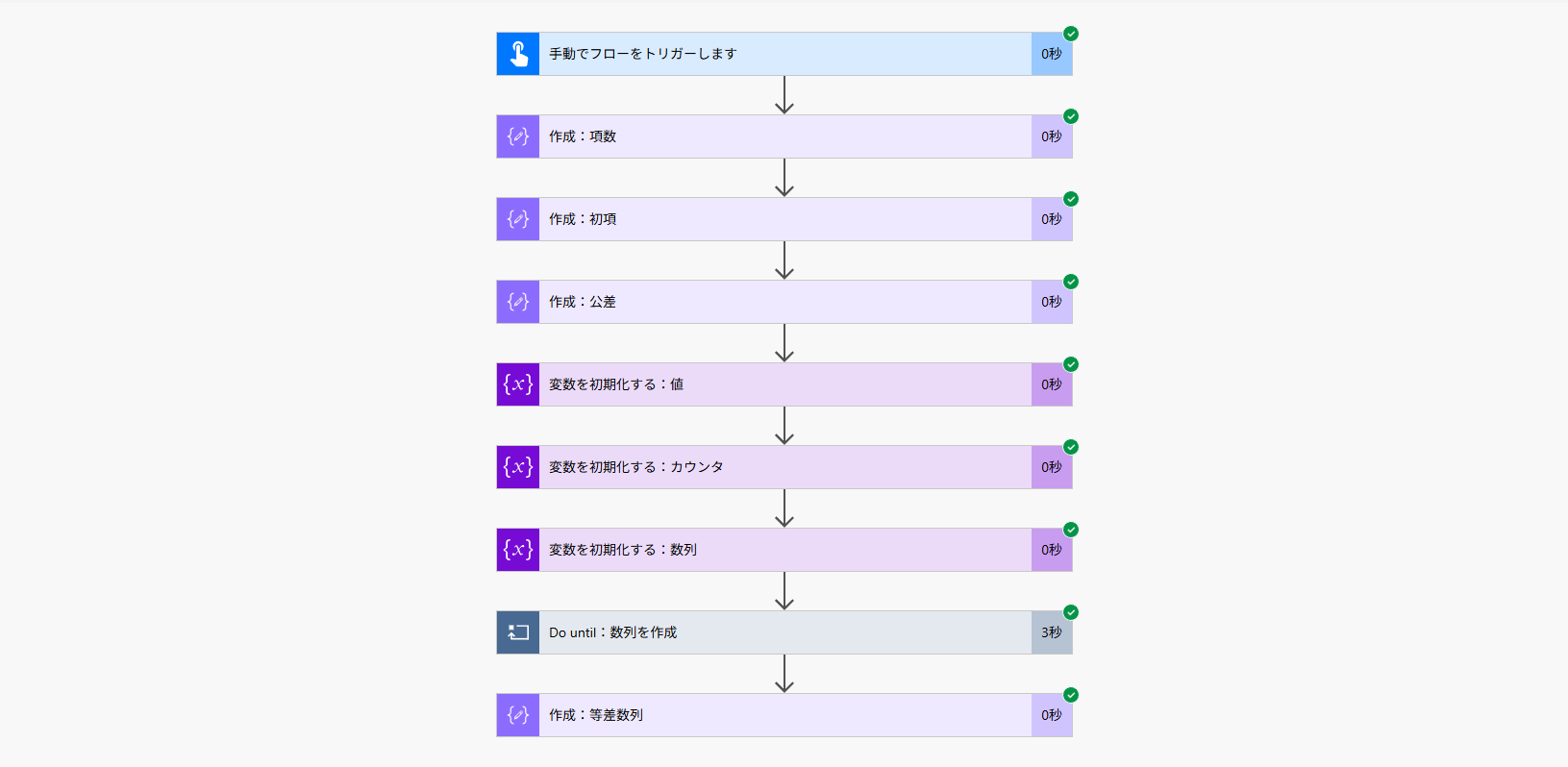
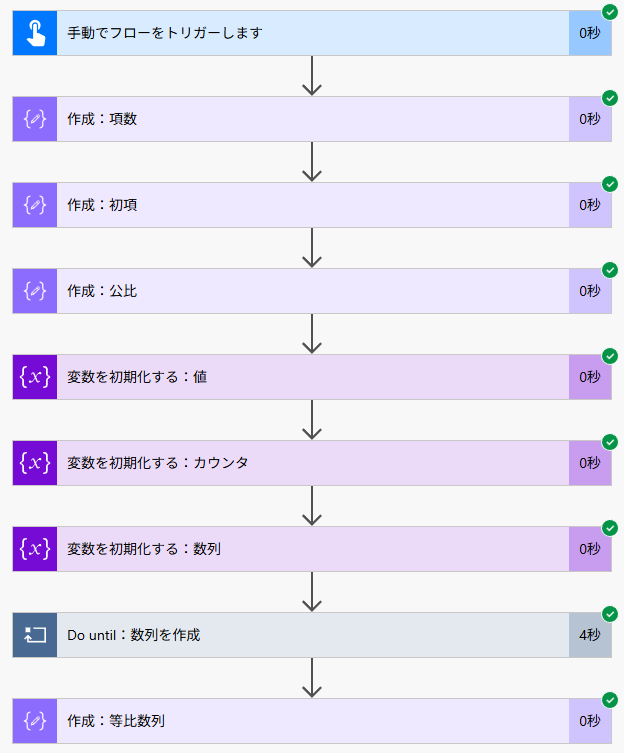
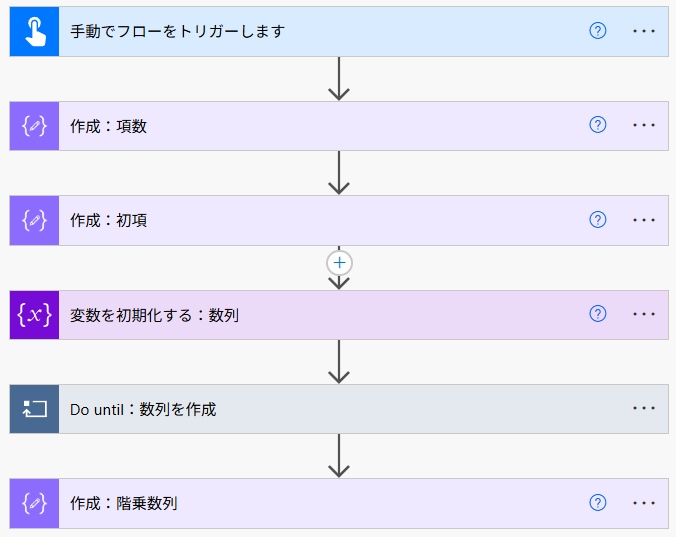
フロー全体図

項数、初項、公差を設定する

まず、いくつ数列を作成するか（項数）、最初の数（初項）、そして間隔（公差）を作成アクションで設定します。

変数を設定する

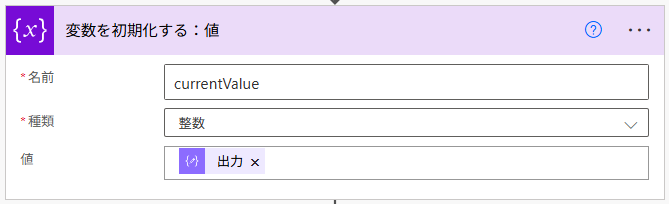
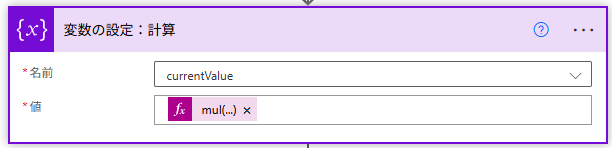
次に、数列の作成に必要な変数を設定します。変数 currentValue は、後続のアクションにて数列を作成するために必要な変数です。正確に言うと、この変数は「数列の中の１つの数」となります。

等差数列は、公差分を加算することで実現できますので、種類（データ型）を「整数」に設定します。また、変数の初期値は直前で作成した「作成：初項」を動的な値として設定しています。

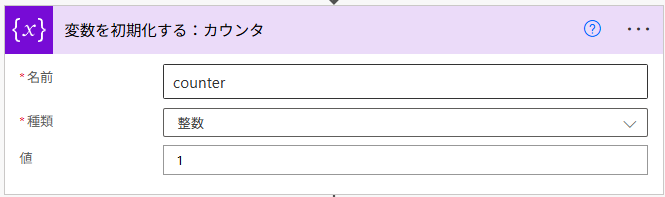
変数 counter は、数列の項数分だけ計算を繰り返す処理を施すために必要です。Do until のセクションで詳細をご説明します。とりあえず、上の画像のように設定をしておいてください。

変数 sequence は、作成した値（計算後の値）を配列化するための変数です。これも詳細は後ほど明らかになっていくものですので、ひとまずは上の画像のように設定しておいてください。

余談ながら、アレイとは「配列」を意味しています。配列とは、表形式のデータのことだと思っておいて差し支えありません。また、Power Automate には、オブジェクトという用語も出てきますが、これは、アレイに含まれる一件々々のデータを意味しています。なお、アレイを示す記号は [ ] で、オブジェクトを示す記号は { } です。ややこしや。このあたりの説明は今回は省きます。

数列の作成

準備ができたところで、実際に数列を作成していきます。「コントロール」から、Do until を挿入し、その中に変数を３つ設定することで等差数列は作成できます。

Do until は、特定の条件が真（true）である限り繰り返しを行い、条件が偽（false）になるとループを終了するタイプの繰り返し処理です。今回でいうと、項数 10 件分の数列を作成したいわけなので、最初に作成した「作成：項数」よりも小さくなるように公差を加算した currentValue を sequence に随時追加していくことになります。

「配列変数に追加」アクションには、公差分が加算された値である currentValue を動的な値から入力します。初回は 1 と設定しているので、初項は 1 となります。次にループする時に currentValue は 1 + 3 の 4 となり、さらにループすると 4 + 3 の 7 が currentValue の値となり、順次、配列変数 sequence に追加されていく仕組みです。

最後、忘れてはならないのが「変数の値を増やす：カウンタ」の設定です。指定した回数分のループ処理を施すため、現在の回数をカウントしておく必要があります。変数 counter はこのために存在しているものです。これにて、等差数列のフローは作成完了です。

文字列化したい場合

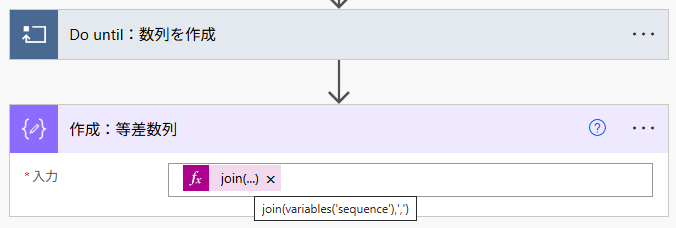
フロー自体は完成ですが、配列（表形式のデータ）を文字列に変換したいという場合が今後あるかもしれません。その時は、Do until の外側に「作成」アクションを配置し、join 関数を使って文字列化します。

join(variables('sequence'),',')

以上で完了です。これを土台として、次は等比数列の解説です。

等比数列

等比数列とは、隣り合う項の比（公比）が一定になる数列のことです。次の例を見てみましょう。

• 項数：10
• 初項：1
• 公比：3

この場合の等比数列は、1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683 です。初項 1 から 公比 3 ずつ、一定に増えていることがわかります。このセクションでは、これを Power Automate で実装してみます。

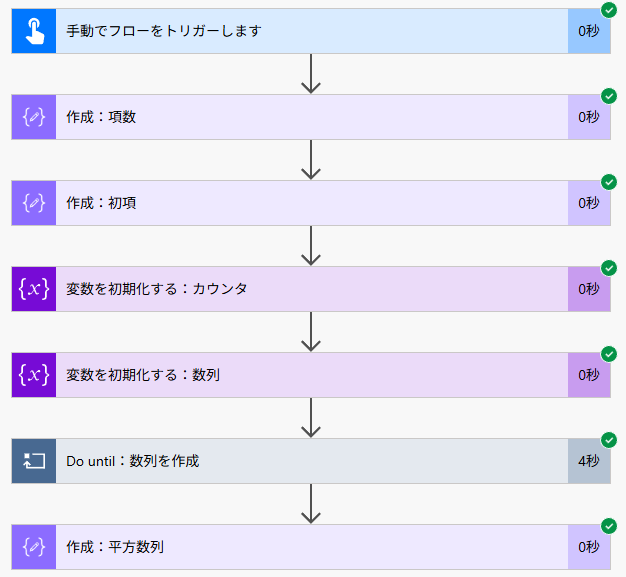
フロー全体図

等差数列と異なる点のみ

フロー全体図を見ていただいた通り、仕組みと作り方自体は等差数列と同じです。異なるのは「Do until」アクション内の変数の設定です。

等差数列の時は、３ずつ増やしていけば良いだけでしたが、今回は「作成：現在のｎ」というアクションがひとつ追加されており、このアクションを後続アクションで公比（今回は３）を乗算しています。具体的には、上から流れてきた currentValue に 3 を掛けた数が、次に sequence に追加する値ということです。

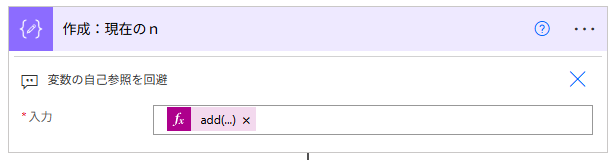
直接「変数の設定」アクションでこの計算をさせる方が余分なアクションを入れずに済むのでフローがスッキリしそうですが、Power Automate では「変数の自己参照」を行うことができません（Power Automate for desktop の方は上手く回るのになあ）

“Template language expression evaluation failed: The input for action 'Set_variable' at line '...' and column '...' is not valid. Self-referential loops are not supported. Action 'Set_variable' references variables('currentValue') in its own definition, which causes a circular dependency.”

ということで、この作成アクションは、流れてきた数の受け皿になってもらっているというわけです。その作成アクションで受け取った値を、後続の変数アクションで次のように設定しています。

mul(outputs('作成：現在のｎ'),outputs('作成：公比'))

これにてフローは完成です。

平方数列

平方数列という呼称は一般的でないかもしれませんが、当記事では、各項が自然数ｎの二乗になる数列のことを指しています。次の例を見てみましょう。

• 項数：10
• 初項：2

この場合の平方数列は、4, 9, 16, 25, 36, 49, 64, 81, 100, 121 です。初項 2 から

• 2^2 = 4
• 3^2 = 9
• 4^2 = 16

...と、一定に増えていることがわかります。このセクションでは、これを Power Automate で実装してみましょう。

フロー全体図

等差、等比数列と異なる点のみ

今回も等比数列の時と同様、変数の自己参照を回避するために緩衝材としての作成アクションを配置しています。こちら、一件ずつ関数を入力しているので、それぞれ見てみましょう。

add(outputs('作成：初項'),variables('counter'))

currentValue には、今回、作成アクションを用いて初項に +1 ずつ加算される仕組みを作ります。最初は 2、次は 3…と、ループの回数分だけ増えるようにしておきます。

mul(outputs('作成：currentValue'),outputs('作成：currentValue'))

この増えた値同士を乗算することで currentValue の二乗を生み出すことができます。あとは、作成した square を配列変数へと追加することで作業完了です。

三角数列

なんか色々と作ってみたくなったので三角数列なるものも考えてみました。この三角数列という呼称も一般的ではないと思いますが、次のような式で成立する数列です。

$$
T_n = \frac{n(n+1)}{2}
$$

この数式は、身近な例でいうと、ボウリングのピンの配置を表す時などに使用されます。ボウリングのピンは 1+2+3+4 行のピラミッド状（格好つければ四角錐断面状）に並んでおり、計10本です。この場合、T₄ = 10 と表せます。

ｎ人が全員と一度ずつ握手する時の回数、スポーツの総当たり戦、レンガやタイルの配置といったあらゆる場所に三角数で説明できそうなものは隠れています。仕組みが分かれば Power Automate でも実装できそうですね。項数 10、初項 1 の場合は、1, 3, 6, 10, 15, 21, 28, 36, 45, 55 という列を成します。

フロー全体図

平方数列と仕組みはよく似ている

仕組みは平方数列の時とよく似ており、今回も「作成：現在のｎ」アクションにて初項に +1 ずつ加算される仕組みを作ります。これが自然数ｎに代入される値です（※変数の自己参照を回避とメモにありますが当フローでは無関係です）

add(outputs('作成：初項'),variables('counter'))

代入する値を定義したら、次は「作成：triangle」アクション内に、公式を関数で表現します。

div(
  mul(
    outputs('作成：現在のｎ'),
    add(outputs('作成：現在のｎ'), 1)
  ),
  2
)

ここで得られた解を、配列変数へと追加するように設定して作業完了です。

階乗数列

まだ何かないかなあ、というところで「階乗」が頭に浮かんだので今度は階乗に挑戦してみましょう。これも一般的ではない呼称だと思いますが、当記事では、以下の例のような数列を指しています。

• 項数：10
• 初項：1

この場合の階乗数列は 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800 です。2!, 3!, 4!, 5!...と並んでいることがわかります。

そういえば、なんで "！（ビックリマーク）" で階乗を表すのだろうと思ってこの機に調べてみたのですが「階乗すると大きな数になってビックリしてしまうから」らしい。本当に？

言語学における "！" は、喜びを意味する間投詞 "io" を縦に連結した合字説が有力ですが、数学記号で使われる "！" は名付け親の感情由来なんですね。おもしろい。

フロー全体図

階乗を Power Automate で表現する方法については少々頭を抱えましたが、直前までの階乗計算に対して次の値を乗算していくことで実装できることに気付きました。ちょっと気持ちいい。

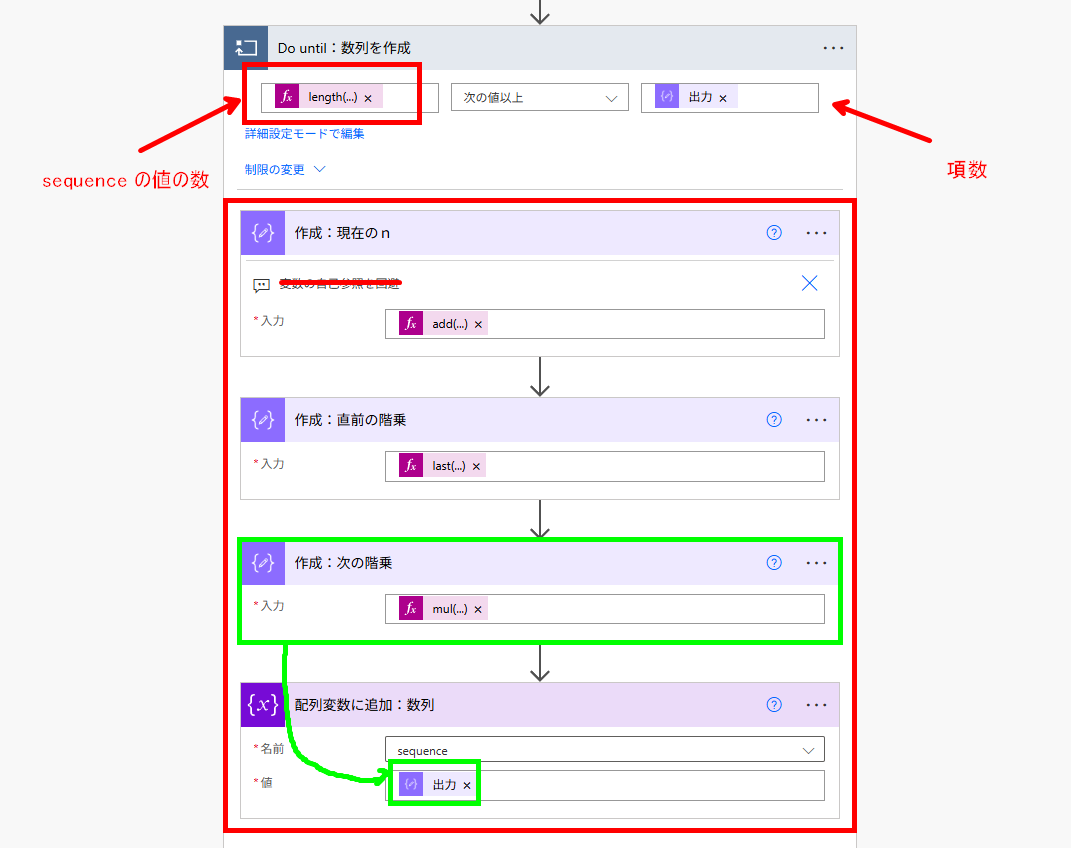
Do until の中身

ということで、実装していきます。まず、Do until の設定がこれまでとは異なります。毎回、while ループの処理を設定するにあたって counter 変数を扱っていましたが、今回は、配列の値の数を counter 代わりに利用してみようと思います（…毎回同じだと芸がない気がして。というか、ここまで読んでいる人はいない気もする）

length(variables('sequence'))

ループの条件の設定を終えたら「作成：現在のｎ」アクション内には次のような設定を施します。前回まで変数 counter に +1 を加算していたものを配列内の値の数に置き換えているだけです。特に意味はありません。

add(length(variables('sequence')),1)

次に、配列変数 sequence 内の、直前の階乗を last 関数を使って取得します。この操作によって、直前までの計算を利用できるようになります。sequence 内の最後に 3! の結果が入っていれば、この 3×2×1 に 4 を掛けるだけで擬似的に 4! を実現できます。

last(variables('sequence'))

取得できたら、このアクションで得た戻り値を利用した乗算を次のアクションで行います。

mul(outputs('作成：直前の階乗'),outputs('作成：現在のｎ'))

この結果を配列変数 sequence に追加して作業完了です。

フィボナッチ数列

数列といえば「フィボナッチ数列」ですね。フィボナッチ数列は、最初の二項を 0 と 1 に定め、以降の各項を直前の二項の和とする数列です。項数 10 の場合、0, 1, 1, 2, 3, 5, 8, 13, 21, 34 という並びになります。

ひまわりの種の配列や松ぼっくりのかさのような螺旋構造、絵画や建築物の黄金比を見るとフィボナッチ数列を思い出します。余談ながら「フィボナッチ」という言葉の響きがかわいい。

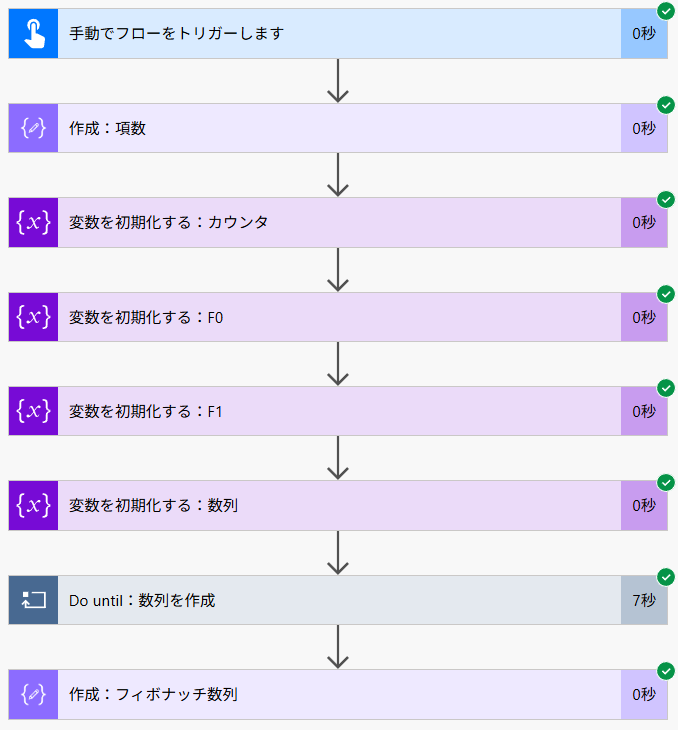
フロー全体図

Do until までの下準備

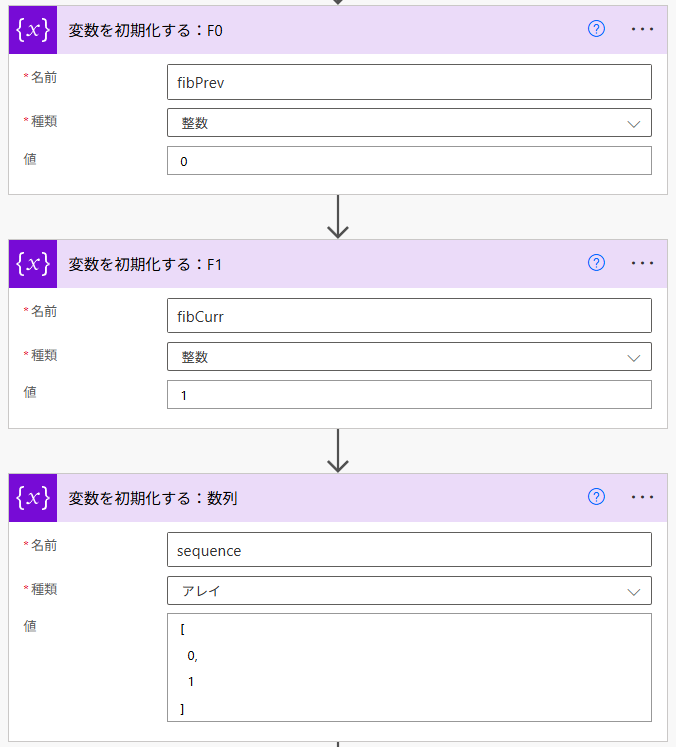
まず、項数を 10（任意）とし、変数 counter の初期値を 2 と設定します。これは、フィボナッチ数列が 0, 1 スタートであるため、項数を調整するために設定しています。

0, 1 以降の各項を直前の二項の和とする数列であることから、直前の項を変数 fibPrev、現在の値を fibCurr で設定し、既に入る値が分かりきっている 0 と 1 をあらかじめ配列変数の sequence に入力しています。

Do until 内部

Do until 内の全体図は次のとおりです。ループの条件部分はこれまでと変わりません。項数分だけのループを設定します。

設定したら、このループ内に「作成」アクションを追加し、この作成アクションで得た戻り値を配列変数 sequence に追加するように設定していきます。

add(
  variables('fibPrev'),
  variables('fibCurr')
)

配列変数に追加したら、前の数（fibPrev）を現在の数（fibCurr）に置き換えるだけです。フィボナッチ数列は「直前の二項の和」なので、１つずつ値をズラしていくだけで作成できてしまいます。

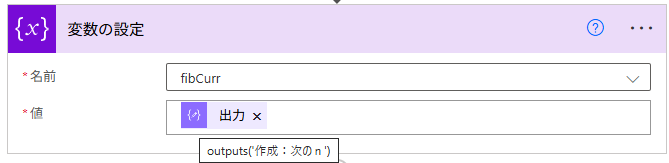
直前の数を置き換えたら、今度は「作成：次のｎ」アクションで集計した値を fibCurr として置き換えてあげます。このようにしてビリヤード方式にズラした値をそれぞれ加算していくことでフィボナッチ数列は生成できます。

最後に counter 変数を 1 増加させることで項数分のループを実現できます。これでフローは完成です。

数列の業務利用

今回、色々な数列を作成してみましたが、実際に業務利用できるもので思い付くのは「偶数番号」や「奇数番号」の取得ではないかなと思います。最後は、業務利用を想定した数列の作成を考えてみます。

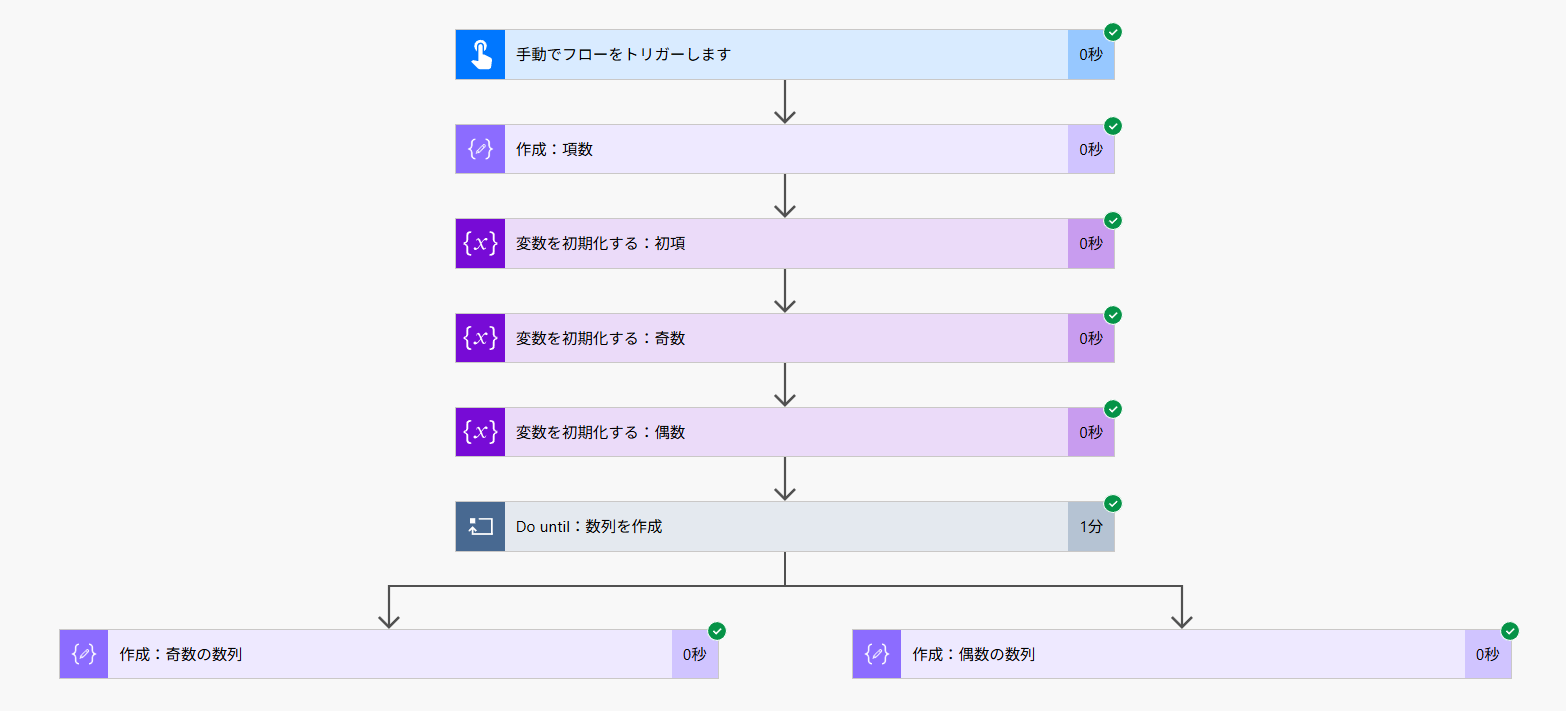
フロー全体図

Do until 内の設定

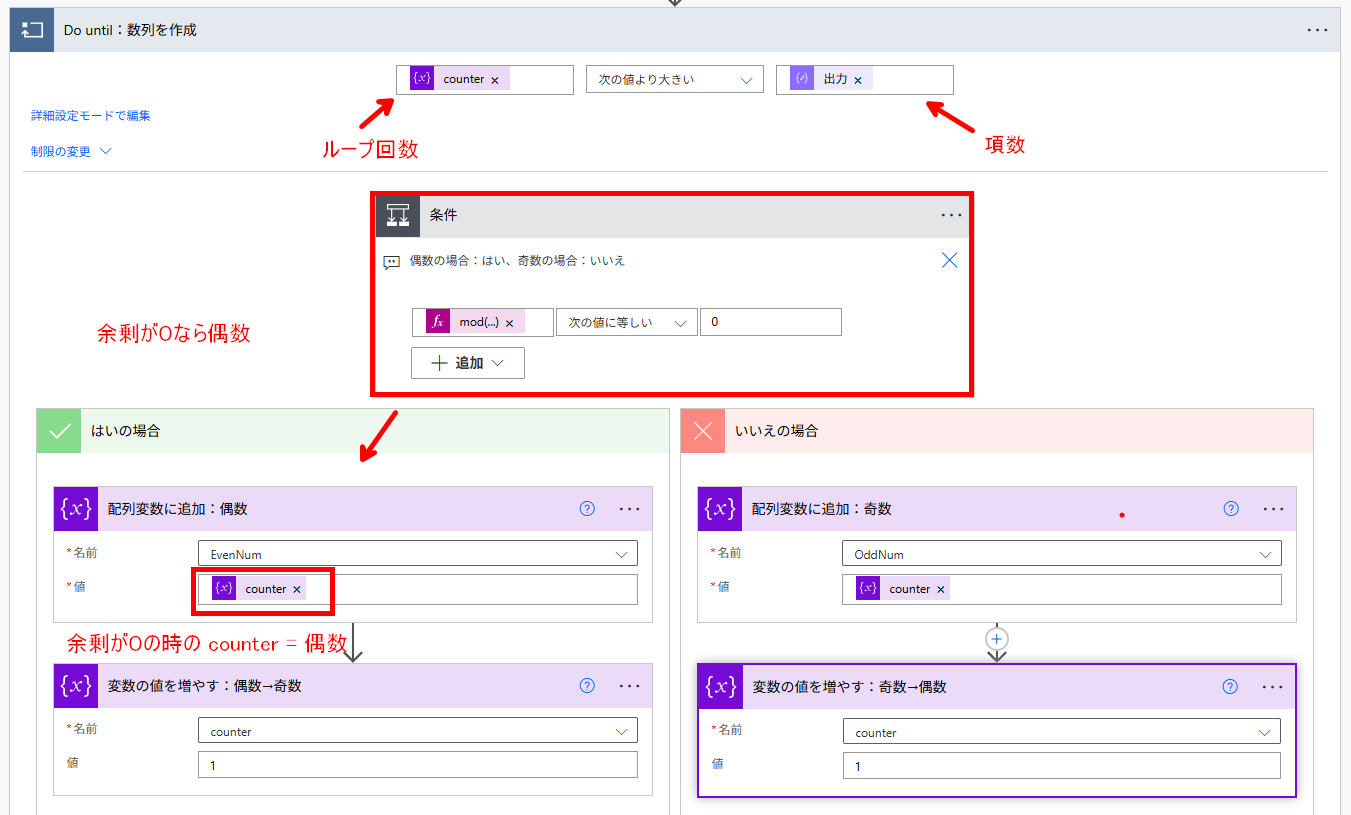
フローの基本構造は、等差数列のそれとほとんど同じです。というか、等差数列なので同じです。Do until 内での設定が肝要になってきます。

条件の左辺部分に次の数式を入力し、その処理の戻り値が 0 だったら「割り切れる数」なので偶数で、そうでなければ「奇数」です。

mod(variables('counter'),2)

あとは、これまでと同様に文字列化していくことで 偶数番号と奇数番号をそれぞれ作成できるようになります。

活用のヒント

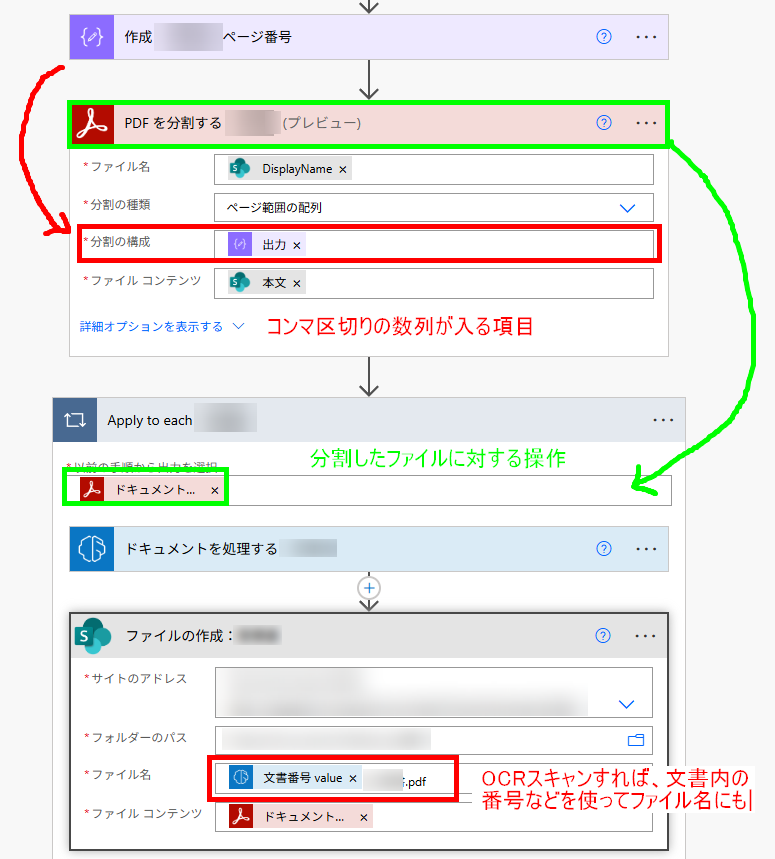
例えばですが、PDF の総ページ分を項数とすれば、その PDF に対する「分割」や「名前をつけて保存」といった操作を可能にしてくれます。２枚１組の PDF ファイルも（法則性さえあれば）分割してそれぞれに名前をつけて保存…ということも実現できます。

AI Builder のクレジットを大量に消費してしまうフローですが、100 ページ分の PDF ファイルに対して 1 件ずつ分割して名前をつけて保存…とするのも中々の苦行な気がします。こういった時に「数列」が役に立つかもしれません。

結：ポエム

「文系だから数学ができない」という声をよく耳にします。筆者はこの言説を「誤解 (myth)」に過ぎないと考えています。数学とは、数字だけを扱う学問ではなく、物事を論理的に組み立て、言語のように考えを構造化する分野であるとも云えるからです。

これは読者の皆さまへの押し付けではなく自戒なのですが、文系のバックグラウンドを持つ人こそ数学を身につけていなければならないはずです。学術だけでなく、あらゆる仕事や趣味においても、文系も理系も無関係に、純粋に「問いを立てて検証する」姿勢が重視されます。しばしば「数学力」と対比で語られる「国語力」は、何も純粋な語彙力だけを示す力ではないためです。

純粋に苦手という人には何も思いません。筆者も不勉強が祟って不得意な部類かもしれません。ただ「文系だから数学ができない」は、見方によっては、そこに論理の飛躍があるだけではなく、文系であることを方便に考えることを避けているようにも捉えられてしまいそうです。その文系が得意とされる「国語力」を備えている人の発言ではないと思われても仕方ありません。

自然言語は（コミュニケーションの観点から）反応速度が重視されますが、数学は（試験でもなければ）時間をかけて考えることが許されています。筆者は日本語以外の言語も習得しているので、多少なりとも多言語習得の困難さを知っている立場です。その立場から見ても、母語以外の言語を習得するよりもじっくりと考えられる数学の方が勉強していて気楽なものです（※できるとは言っていません。それに「深み」にハマると大変な分野です）

さてさて、本記事でご紹介した数列生成の基礎研究が、皆さんの自動化やアイディア創出の出発点となり、深めていく中で新たな発見につながることを願っています。

それでは、また。