概要
3Dを扱っていると頻繁に出てくる回転。
回転行列だったり、クォータニオンだったり。あるいはオイラー角を使ってみたり。
コンテンツを作る上である程度把握して使ってはいるものの、たまにハマったり、なんでそういう動きになるんだろう?
みたいなことがあります。
3Dコンテンツを作っていて回転を行うとき、いたるところで三角関数が顔を出してきます。
ということで、三角関数のあれこれをまとめておこうと思います。
また実際に計算を行うにしても、色々な定理や理論を知っておくことはとても有用だと思います。
ということで、今回は回転に関する数学的な話をざっとまとめていきます。
順不同、適当な感じでメモしていきます。
三角関数の一般角での定義
通常、三角関数は直角三角形についてのみ成り立つ関数です。
しかしそれでは3Dの世界はもとより、その他の場面でも不便になります。
そこで、三角関数を拡張し、直角三角形の対角が鈍角になる場合でも成り立つように再定義する必要があります。
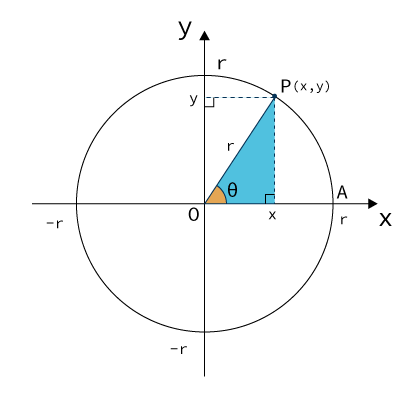
まず、以下の図を見てください。
$x$軸の正の方向を始線とし、そこから$\theta$だけ回転した線と、半径$r$の円との交点を$P(x, y)$とした図です。
このとき、$\frac{y}{r}, \frac{x}{r}, \frac{y}{x}$は円の半径に関係なく、$\theta$のみで決まるため、三角比と同じように以下のように定義します。
\sin\theta = \frac{y}{r} \\
\cos\theta = \frac{x}{r} \\
\tan\theta = \frac{y}{x}
さらに半径$r$が$1$、つまり単位円のとき、単純に以下のようになります。
\sin\theta = y \\
\cos\theta = x \\
\tan\theta = \frac{y}{x}
※ ただし、図を見て分かるように左半分は$x$軸が$-r$、下半分は$y$軸が$-r$となるため、正負が逆になります。
実際に数値を見てみると、確かに$\sin{90^\circ} = 1$、$\cos{0^\circ} = 1$となりますね。
これを用いれば、直角三角形以外にも三角関数を用いて計算を行うことができるようになります。
弧度法
角度には度数表記と弧度表記があります。
度数は円が一周で360度とするものですね。
対して弧度法は「ラジアン」を単位とする表現方法です。
度数表記には数学的な根拠がない値のため、色々とめんどくさいらしいです。
そこでよく使われるのが弧度法、ということです。
ちなみに定義は以下のようになっています。
\theta = \frac{l}{r}
$l$は円弧の長さ、$r$は円の半径です。
そして半径$1$の単位円を考えるとき、$\theta = l$となり、円周は「直径×円周率」なので$2\pi=360°$となります。
正弦定理
正弦定理とは。
Wikipediaから引用させてもらうと、
正弦定理(せいげんていり、law of sines)とは三角形の内角の正弦(サイン)とその対辺の長さの関係を示したものである。正弦法則ともいう。多くの場合、平面三角法における定理を指すが、球面三角法などでも類似の定理が知られており、同じように正弦定理と呼ばれている。
$\triangle ABC$ において、$BC = a, CA = b, AB = c$, 外接円の半径を $R$ とすると、
$\frac{a}{\sin A}=\frac {b}{\sin B}=\frac {c}{\sin C}=2R$
が成り立つという定理である。これより一辺とその両端の角から他の二辺が分かり、三角測量の基礎となっている定理である。
上記の定理から、式を変形すると$\sin A = \frac{a}{2R}$となります。
同じく、Wikipediaに載っている証明を見てみましょう。
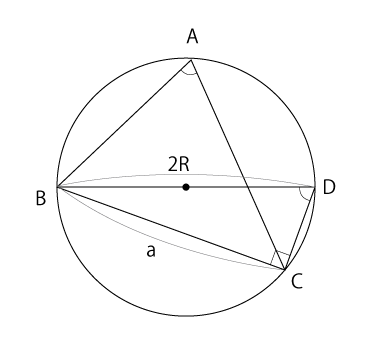
正弦定理の証明
$0 < ∠A < \frac{π}{2}$ のとき
直径 BD を取る。円周角の定理より ∠A = ∠D
△BDC において、BD は直径だから、
BD=2R, \angle BCD = \frac{\pi}{2}
よって、正弦の定義より、
\sin D={\frac {a}{2R}}
ゆえに
\sin A=\sin D={\frac {a}{2R}}
変形すると
\frac{a}{A} = 2R
が得られる。
$\sin D={\frac {a}{2R}}$ は、直角三角形に対する角度のため、三角関数の通常の正弦の定義から明らかです。
そして、$sinA$ は、$sinD$ と角度が同じため、結果は変わりません。
そこから、$sinA = sinD$ が導かれます。
つまり $sinA = sinD = \frac{a}{2R}$ が導かれます。
図にすると以下のようになります。
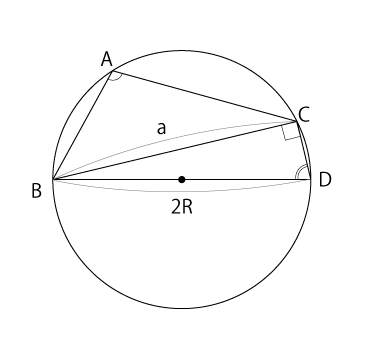
また、上記は鋭角の場合の証明です。
鈍角の場合は以下のようになります。
$\frac{\pi}{2} < ∠A < \pi$ のとき
直径 BD を取る。
円に内接する四角形の性質から、
\angle D = \pi -\angle A
つまり、
\sin A = \sin D
となる。 BD は直径だから、
BD = 2R, \angle BCD = \frac {\pi}{2}
よって、正弦の定義より、
\sin A = \sin D = \frac {a}{2R}
変形すると
\frac {a}{\sin A} = 2R
が得られる。$\angle{B}, \angle{C}$ についても同様に示される。
以上より正弦定理が成り立つ。
図にすると以下のようになります。
内接する四角形の性質
内接する四角形にはいくつかの性質があります。
(こちらの記事(円に内接する四角形の性質とその証明まとめ)を参考にしました)
その中で、「角度の和」の性質があります。
上記記事から引用させてもらうと、
性質1:向かい合う内角の和は 180° である。つまり,
\angle A + \angle C = 180°
\angle B + \angle D = 180°
これを証明すると、以下になります。(こちらも引用)
証明
円周角と中心角の関係より
$\angle A + \angle C = \frac{1}{2} × 360° = 180°$
「円周角の定理」は下で説明します。
ちなみに、「$\angle D = \pi -\angle A$」という記載がありますが、結局のところ、$\angle D$ と $\angle A$ の間には180°の差がある、ということを言っているわけです。
そして、180°回転した$\sin$の値はプラス・マイナスが反転するだけですが、よくみると、元の角度の「マイナスの」角度から180°回転しているため、マイナス x マイナスで、結果として同じ値になる、というわけなんですね。
円周角の定理
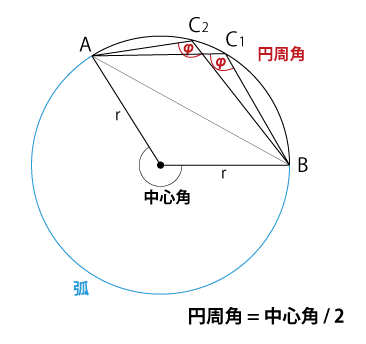
証明の中に出てきた「円周角の定理」も少し見てみましょう。
Wikipediaから引用させてもらうと、
円周角(えんしゅうかく)とは、ユークリッド幾何学においてある円周上の一点から、この点を含まない円周上の異なる二点へそれぞれ線分を引くとき、その二つの線分のなす角のことである。円周角 C (rad) は 0<C<π を満たす。
円周上にとる点の位置に関わりなく、円周角の大きさ C は対応する円弧を含む扇形の中心角の大きさ α のみに依存し、以下のように表わされる。
C={\frac {\alpha }{2}}
>すなわち $a=2C$
>これは円周角の定理として知られる。
まず、円周上に一点(C)を取り、それとは重ならない(異なる)ふたつの点(A, B)を取ります。
そして点CからA, Bそれぞれに線分を引くと、線分ふたつによる角ができます。これが「円周角」です。
円周角の定理とは、この角度における定理となります。
そしてその定理とは、上記で仮定した3点の取り方に関係なく、円周角は点A, Bから円の中心へ線分を書き、その線分と点B, C端点とする円弧を含む「扇形の中心角$α$の大きさのみに依存する、というものです。
そこから、円周角Cは、$C = \frac{\alpha}{2}$ 変形して $\alpha = 2C$という定理が導き出されます。
このことから、正弦定理の「$ \angle A = \angle D$」が成り立っているというわけですね。
## 余弦定理
[余弦定理](https://ja.wikipedia.org/wiki/%E4%BD%99%E5%BC%A6%E5%AE%9A%E7%90%86)とは。
Wikipediaから引用させてもらうと、
>余弦定理(よげんていり、英: law of cosines, cosine formula)とは、平面上の三角法において三角形の辺の長さと内角の余弦の間に成り立つ関係を与える定理である。余弦定理を証明するために用いられる補題はときに第一余弦定理と呼ばれ、このとき証明される定理は第二余弦定理と呼ばれ区別されることがある。単に余弦定理と言った場合、第二定理を指す。
要はコサインを利用して三角形の辺の長さや角度を求めるもの、という感じでしょうか。
三平方の定理は以下でした。
```math
a^2 = b^2 + c^2
しかしこれは直角三角形だけで成り立つため、それ以外の角にはそのまま当てはめることができません。
つまり、これを一般角にまで拡張するために必要な理論となります。
まずは公式を示すと以下になります。
a^2 = b^2 + c^2 - 2bc \cos{A}
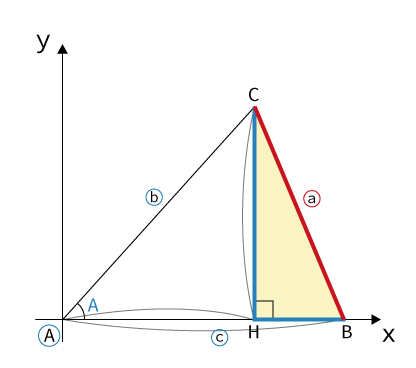
これを導くには、以下の図を見てもらうと分かりやすいと思います。
図のように、直角でない三角形に対し、頂点$C$から鱗片に対して垂線をおろします。
するとふたつの直角三角形に分解することができます。
すると、$\triangle AHC$は直角三角形のため、
\sin{A} = \frac{CH}{b} → CH=b\sin{A} \\
\cos{A} = \frac{AH}{b} → AH=b\cos{A} → BH=c-b\cos{A}
となります。
これで$CH$と$BH$を求めることができるようになったので、あとは三平方の定理から$a$を導くことができるようになります。
計算すると以下のようになります。
a^2 = CH^2 + BH^2 \\
= (b \sin{A})^2 + (c - b \cos{A})^2 \\
= b^2 \sin^2{A} + c^2 - 2bc\cos{A} + b^2 \cos^2{A} \\
= b^2(\sin^2{A} + \cos^2{A}) - 2bc\cos{A} + c^2
そして、$\sin^2{A} + \cos^2{A} = 1$となるため、最初に示した公式が導き出されます。
a^2 = b^2 + c^2 - 2bc \cos{A}
加法定理
三角関数の値を求める際、角度を増やしたり減らしたりしたい場合、たんにそれぞれ求めた結果をプラスマイナスしても正解にはなりません。
正確な値を求めるためにはこの「加法定理」を用いる必要があります。
公式は以下になります。(複号同順)
\sin(\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\
\cos(\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta
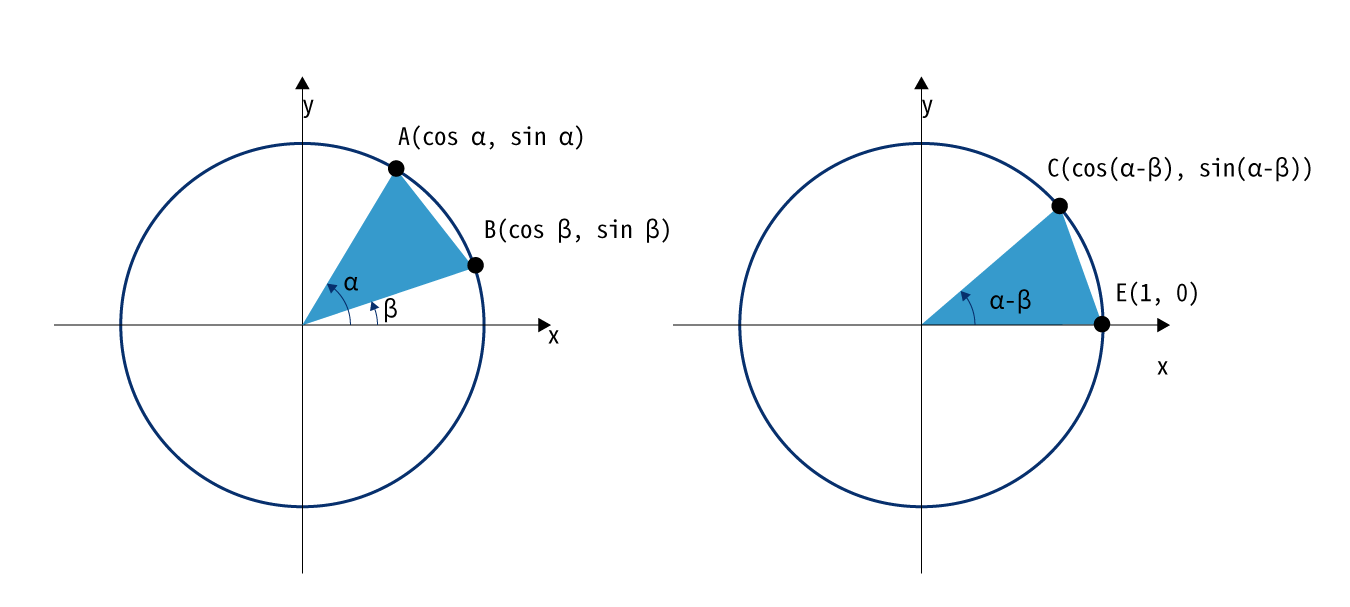
これを証明するには、以下の図を見てもらうとイメージしやすいと思います。
まず、左図を見てみると角$\alpha$と$\beta$に対する単位円上の点はそれぞれ$A(\cos \alpha, \sin \alpha)$、$B(\cos \beta, \sin \beta)$となります。これはたんなる三角関数から求められますね。
さて、今$\alpha$と$\beta$を合成したいわけなので、右図のように位置を変形してみます。
すると、それぞれの値は$C(\cos (\alpha - \beta), \sin(\alpha - \beta))$、$E(1, 0)$と置くことができます。
(右図の角度が$\alpha - \beta$になるので、たんにそれを角度として三角関数から求めただけですね)
同じ位置にある点を角度だけ移動したため、左と右の三角形は合同となります。
つまり、各辺の長さはどちらも同じため$AB^2 = CE^2$が成り立ちます。
辺$AB$と辺$CE$はベクトルと見ることができるため、以下のように計算できます。
(\cos{\alpha} - \cos{\beta})^2 + (\sin{\alpha} - \sin{\beta})^2 = (\cos({\alpha - \beta}) - 1)^2 + \sin^2({\alpha - \beta})
ベクトルの$x, y$成分を引き算で求めて、辺$AB$と辺$CE$を計算して、それぞれの二乗を計算しているだけです。
あとはこれを展開、整理すると最初の公式が導き出される、というわけです。やってみましょう。
\cos^2\alpha - 2\cos\alpha\cos\beta + \cos^2\beta + \sin^2\alpha - 2\sin\alpha\sin\beta + \sin^2\beta = \cos^2(\alpha - \beta) - 2\cos(\alpha - \beta) + 1 + \sin^2(\alpha - \beta)
これを、$\sin^2\theta + \cos^2\theta = 1$などを使って整理すると、
\cos(\alpha - \beta) = \cos\alpha\cos\beta + \sin\alpha\sin\beta
となります。