概要
今回はShadertoyで見かけたこちらの作品のコードリーディングをしてみようと思います。
ちなみに、これを解読してちょっとコード整理しつつ音に反応して見るようにしてみました↓
解説
まずはコード全体を。そんなに長くありません。
float burn;
mat2 rot(float a)
{
float s = sin(a);
float c = cos(a);
return mat2(s, c, -c, s);
}
float map(vec3 p)
{
vec3 p1 = abs(p);
// ========================================
// Render the cube.
float cubeSize = 0.5;
float d1 = max(max(p1.x, p1.y), p1.z) - cubeSize;
// ========================================
// Rotate grids.
mat2 rm = rot(-iTime / 3.0 + length(p));
p.xy *= rm;
p.zy *= rm;
// PingPon on 0.5
vec3 q = abs(p) - iTime;
q = abs(q - round(q));
rm = rot(iTime);
q.xy *= rm;
q.xz *= rm;
// ========================================
// Render grids space.
float l1 = length(q.xy); // Plane XY
float l2 = length(q.yz); // Plane YZ
float l3 = length(q.xz); // Plane XZ
float gridOffs = 0.01;
float d2 = min(min(l1, l2), l3) + gridOffs;
burn = pow(d2 - d1, 2.0);
return min(d1, d2);
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = (2.0 * fragCoord - iResolution.xy);
vec3 rd = normalize(vec3(uv, iResolution.y));
vec3 ro = vec3(0, 0, -2);
// Rotate ray position and ray target.
mat2 r1 = rot(iTime / 4.0);
rd.xz *= r1;
ro.xz *= r1;
mat2 r2 = rot(iTime / 2.0);
rd.yz *= r2;
ro.yz *= r2;
float t = 0.0;
float i = 30.0 * (1.0 - exp(-0.2 * iTime - 0.1));
for(; i-- > 0.0;)
{
t += map(ro + rd * t) / 2.0;
}
fragColor = vec4(1.0 - burn, exp(-t), 2.0 * exp(-t / 4.0 - 1.0), 1.0);
}
理解を促すために最初にポイントを書いておくと、
- Cubeの(ちょっとトリッキーな)距離関数でCubeを描く
- 軸に沿ったラインを求める距離関数を視点を回転させてエモくする
- それを合成する
というような流れです。
では、まずはmainImage関数から順番に見ていきましょう。
(念のため補足しておくとShadertoyにおいてこのメソッドがエントリーポイントになります)
メイン関数冒頭のrotは視点の回転
冒頭で以下のようにベクトルを回転させています。
mat2 r1 = rot(iTime / 4.0);
rd.xz *= r1;
ro.xz *= r1;
mat2 r2 = rot(iTime / 2.0);
rd.yz *= r2;
ro.yz *= r2;
これは、レイの位置と注視点を回転させています。
これをコメントアウトしてもエフェクトのイメージはそこまで変わりません。
大きく変化が出るのは中央のCubeが回る部分ですね。
内容自体はシンプルです。
レイマーチの回数は時間で急激に増加するが、一定値以上はほぼ横ばい
さて、次はレイマーチのループ部分です。
レイマーチの回数iの部分が、ちょっと複雑な計算によって行われています。
float i = 30.0 * (1.0 - exp(-0.2 * iTime - 0.1));
一瞬、なにをやっているのか分かりづらいですが、これをグラフにすると見えてきます。
グラフ化したのが以下です↓
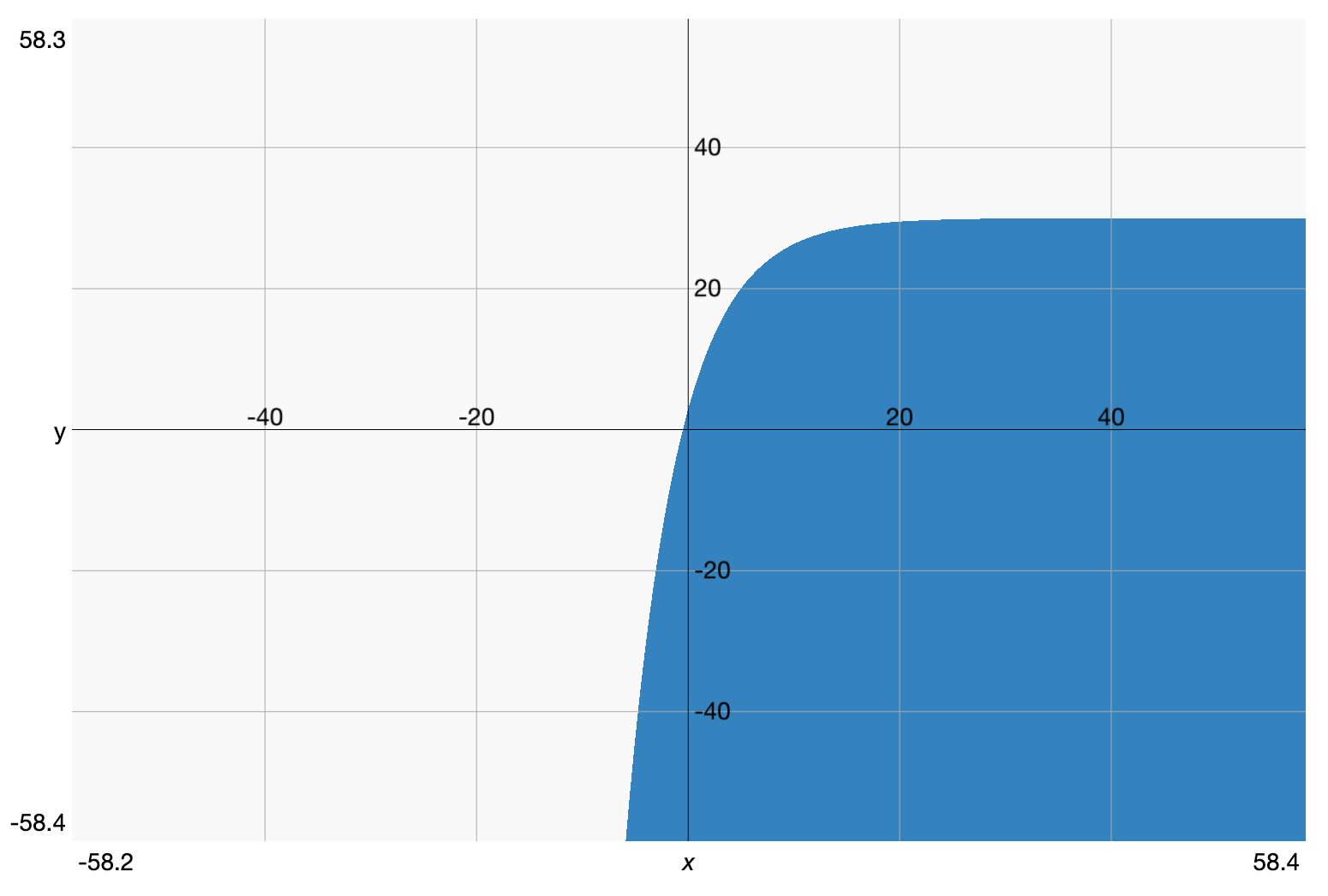
これを見ると、x(つまりiTime)の増加によって、最初は急激に上昇していますが、一定値を超えるとほぼ横ばいとなっているのが分かります。
計算式の中でexpを使っていることからもなんとなくイメージできるかと思います。
要は、冒頭と後半で見た目を大きく変えている、と考えるといいかと思います。
なので、解読後に自分で作った方はループ回数を固定にしていますが、見た目の変化はほとんどありません。
色の決定
ループ内のmap関数はあとに回すとして、最後の色を決定する部分を見てみましょう。
fragColor = vec4(1.0 - burn, exp(-t), 2.0 * exp(-t / 4.0 - 1.0), 1.0);
burn変数は関数外で定義されています。map関数内で更新される想定のものになっています。
burnが使われているのはr要素だけなので、つまりはレイマーチの距離に応じて赤みが変化する、という感じですね。
残りのgb要素はレイマーチの距離結果(t)をそのまま使い、exp関数によって値が変化するようになっています。
これをグラフにすると以下のようになります。
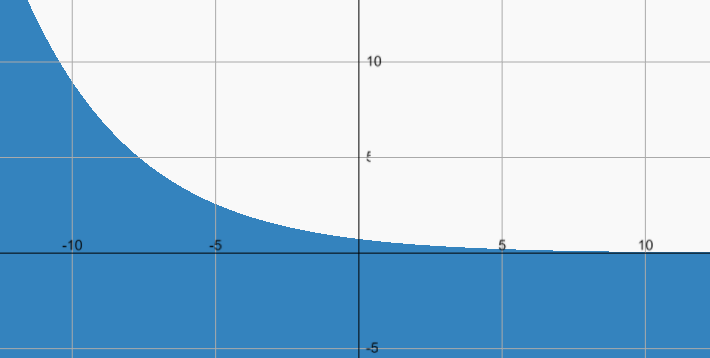
グラフを見ると分かりますが、tの値が小さいほど大きく、逆に大きくなるほど小さくなっていきます。
つまりは画面に近いあたりの部分は青くなる、というようなイメージですね。
ちなみに白黒だけにするとこんな感じ。これはこれでかっこいいですね。

map関数の中を見る
さて、次からはいよいよ本丸、map関数の中を見ていきましょう。
ちょっと特殊なBoxの距離関数
map関数の冒頭で行われている計算は一瞬難解な感じですがただのBoxの距離関数です。
float d = max(max(abs(p.x), abs(p.y)), abs(p.z)) - 0.5;
そして最後の-0.5がBoxのサイズですね。
これを少し分かりやすく整形すると以下のようになります。
vec3 p1 = abs(p);
float d = max(max(p.x, p.y), p.z) - 0.5;
pの絶対値を取り、さらにxyz要素の中で最大のものを採用します。
これはつまり、原点から各軸の距離を測っていることになります。
そして-0.5とすることで、各軸が0.5だけオフセットします。
理解を簡単にするためにXY平面に限って考えてみると分かりやすいです。
XY軸上で、原点からの距離を測り、さらにそこから-0.5すると、以下のようになりますね。
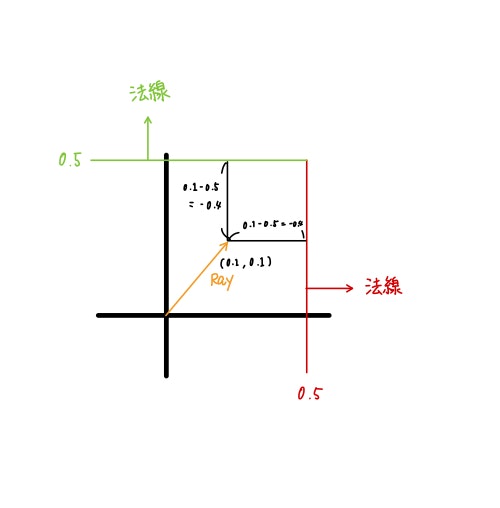
つまり、XY平面上でいうと赤い線と緑の線が地平線となっていて、まだベクトルが小さいときはマイナスになります。(=地平線の下にいる)
それがある程度進むと地平線の上に出て、あとは普通に平面との距離計算になる、というわけですね。
そしてそれをmaxによるAND合成することでBoxが描かれる、というわけです。
イメージ的には上の図で書いた方向に法線を持った3平面を合成するとBoxが現れる、というわけです。
(absによって折りたたんでいるため、結果、全方位を平面が囲んでいるような状態になります)
0.0~0.5~0.0で往復
これを見たときはちょっと驚きました。
だいぶスマートに0.0~0.5~0.0を往復させています。
コードは以下。
vec3 q = abs(p) - iTime;
q = abs(q - round(q));
こちらの計算。roundは四捨五入をする関数です。
つまり、qの値が0.4までは0.4 - 0となって0.4となります。
一方、0.5を超えると0.55 - 1.0となって、0.45(absなので絶対値)となり、値が大きくなるにつれて今度は0に近づいて行くことになります。(0.9のときは0.9 - 1.0 = 0.1)
また、qの値が極端に大きくても相殺されて常に0.5の範囲にとどまる、というのもポイントです。
この計算の意図は、レイの位置pを折りたたんでいる、と考えるといいと思います。
XYZ軸それぞれへの距離の合成でグリッドを表現
次はグリッド表示の部分です。(実際にはこれを歪ませているのでグリッドには感じませんが)
次のコードを見てください。
// PingPon on 0.5
vec3 q = abs(p) - iTime;
q = abs(q - round(q));
rm = rot(iTime);
q.xy *= rm;
q.xz *= rm;
float l1 = length(q.xy); // Plane XY
float l2 = length(q.yz); // Plane YZ
float l3 = length(q.xz); // Plane XZ
float d2 = min(d1, min(min(l1, l2), l3) + .01);
冒頭の部分は前述の0.5で往復する、という前述の部分ですね。
これによってレイの位置を折りたたみます。
その下の回転は視点回転なので飛ばして、l1〜l3の変数部分に注目してください。
それぞれ、XY平面、YZ平面、XZ平面と3つの面に限定したベクトルの長さを測っています。
これは(おそらく)基底の軸との距離関数だと思われます。
試しにXY平面のベクトルについて考えてみましょう。
3次元ベクトルのXY要素のみ、ということはつまり、そのベクトルをXY平面に投影したもの、と考えることができます。
つまり、
vec3 p = vec3(1, 1, 1); // というベクトルがあったとして
p.z = 0.0; // と、Zの値を0にしているのに等しい
さて、ではこの「XY平面のベクトル」の長さはなにとの距離なのか。
それは「Z軸」との距離になります。
なぜなら、XY平面はZ軸に垂直だからです。なのでそのままベクトルの長さがZ軸との距離になる、というわけですね。
そしてそれ以外の平面についても考え方は同様です。
最後にそれをminによって合成しています。
ちなみに最後の0.01は線の太さを表しています。
なのでなんとなく線が引かれるイメージが湧いてきませんか?
加えて、評価しているベクトルqはabsにより折り畳まれているのと、roundによるトリックで0〜0.5〜0を行き来しています。
つまり「繰り返し」が現れているということですね。
ということで、この表現部分だけを抜き出して視覚化したのが以下のものです。
繰り返しによって無限のグリッドが表示されているのが分かるかと思います。
非常にシンプルなのにこうした絵が出てくるのは本当に面白いですね。
ちなみにこちらもShadertoyにも上げてあります。
rot関数によって視点を曲げる
グリッドが理解できたらあと少しです。
このグリッド上の表現をrot関数によって曲げることで、冒頭のようなカッコいいエフェクトに変化させている、というわけなんですね。
// ========================================
// Rotate grids.
mat2 rm = rot(-iTime / 3.0 + length(p));
p.xy *= rm;
p.zy *= rm;
// PingPon on 0.5
vec3 q = abs(p) - iTime;
q = abs(q - round(q));
rm = rot(iTime);
q.xy *= rm;
q.xz *= rm;
ちなみにこの回転をオフにしてみると以下のような絵になります。

なんとなくグリッドがうっすらと見えているのが分かるかと思います。
同じタイミングで、視点の回転を入れると以下のような感じになります。
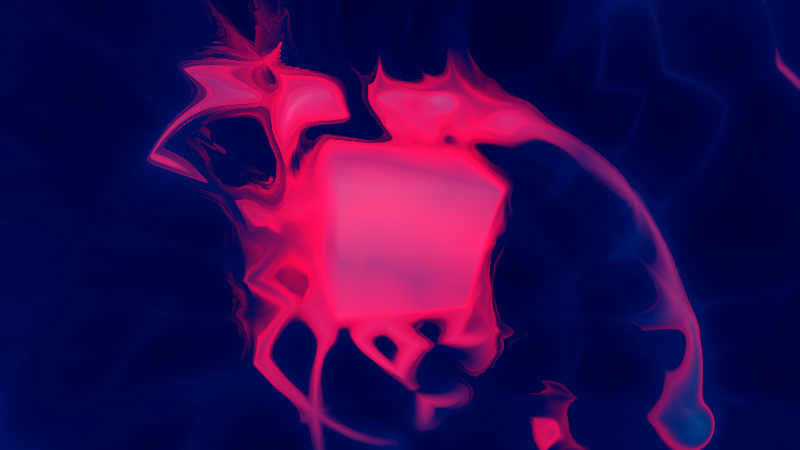
ぐにゃっと曲がっているのがなんとなく分かるかと思います。
この歪みを表現しているコツは以下の部分です。
mat2 rm = rot(-iTime / 3.0 + length(p));
rot関数の引数に渡している値計算のうち、length(p)がそのポイントです。
これは、レイの位置に応じて変化する値になりますよね。
そして外に飛んでいけばいくほど値は大きくなります。(レイの進む距離が大きくなるから)
つまり、画面の際にいくほど大きく歪むように調整している、というわけです。
まとめ
いかがだったでしょうか。
非常にシンプルなコードの中に学びがたくさんありました。
Shadertoyの作品はこの手のテクニックの宝庫なので、気に入った表現をこうして読み解いて行くととても学びが多いし、またそれを応用して自分自身でもカッコいい作品が作れるようになっていくのでオススメです。


