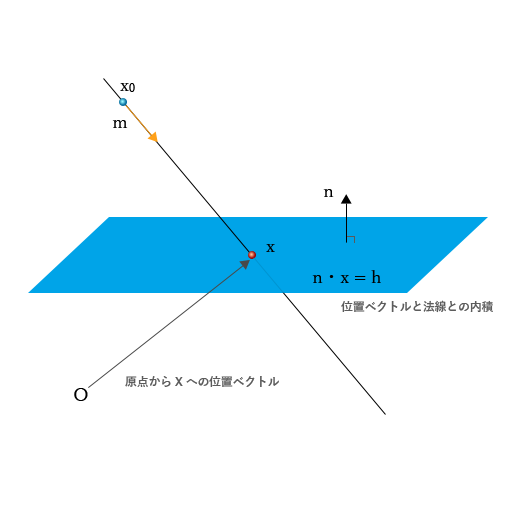
通常の Plane オブジェクトとの交差判定ならレイキャストを使って表現するのが手っ取り早いですが、例えば擬似的に、無限遠に存在する平面に対してどこを指し示しているか、というのが分かると便利そうです。
ということで、その実装です。
(こちらの記事を参考にしました)
上記の記事から引用させてもらうと、式は以下になります。
// 平面 \\
(n, x) = h
// 直線 \\
x_0 + tm
// 交点 \\
x_0 + \frac{h - (n \cdot x_0)}{n \cdot m}m
ここで $n$ は平面の法線、 $x$ は「平面上の任意の点」、 $x_0$ は起点となる点、$t$ はいわゆる「媒介変数」。$m$ は起点から平面に向かうベクトル、そして $h$ は符号付き距離となります。
Unityベースのプログラムで言えばそれぞれは以下の意味となります。
- $n$ ... 法線。
GameObjectを利用するならtransform.forwardなどを利用する。(もちろん、new Vector3してもいい) - $x$ ... plane.transform.position。交点を求めたい平面上にある「任意の点」。
transform.positionも当然平面に含まれるため、これをそのまま利用する。 - $h$ ... 上記ふたつのベクトルの内積。具体的には法線の射影した位置ベクトルの長さ。
- $x_0$ ... transform.position 始点としたいオブジェクトの位置。(もちろん
new Vector3でプログラム上で生成した点でもOK) - $m$ ... transform.forward 始点から平面へ向かうベクトル。もちr(以下略)。
解説
さて、上記式の導出ですが、以下のように考えます。
基本的な考え方として大事なポイントは、
- 平面上の任意の点は、始点から平面に向かうベクトルに沿って進めていく中にある
- 平面上の任意の点は、平面の法線との内積を取ると必ず同じ値になる(こちらの記事を参照)
という点です。
(2)の平面上の任意の点と平面法線との内積が同じになるのは、任意の点が「原点」からの位置ベクトルとして考えると、位置ベクトルを法線に射影するとすべて同じ距離、つまり平面の点の集まりとなることがイメージできるかと思います。
そして上記理由から $n \cdot (x_0 + tm) = h$ もまた成り立つことを利用して、媒介変数である t の値を求めることができます。
ひとつずつ展開していくと以下のようになります。
n \cdot (x_0 + tm) = h \\
(n \cdot x_0) + (n \cdot tm) = h \\
(n \cdot tm) = h - (n \cdot x_0) \\
t = \frac{h - (n \cdot x_0)}{(n \cdot m)}
となります。
t の値が求まれば、あとは始点と方向ベクトルに t を掛けてやることで交点を求めることができる、というわけです。
ちなみにここで $h$ が未知な感じがしますが、実は $n \cdot x$ の $x$ は平面上の任意の点なので平面の位置ベクトルを使って求めることができます。
これを実行すると以下のように、擬似的に無限に広がる平面に対しての位置を求めることができるようになります。
見てもらうと分かるように、見た目の平面上だけでなく、そこから外れても平面に相当する場所に球体が移動しているのが分かるかと思います。
最後に、ここで利用したコードを全文載せておきます。
using UnityEngine;
using System.Collections;
public class PlaneSample2 : MonoBehaviour
{
public GameObject StartPoint;
public GameObject Plane;
public GameObject Pointer;
// Update is called once per frame
void Update ()
{
var n = Plane.transform.up;
var x = Plane.transform.position;
var x0 = StartPoint.transform.position;
var m = StartPoint.transform.forward;
var h = Vector3.Dot(n, x);
var intersectPoint = x0 + ((h - Vector3.Dot(n, x0)) / (Vector3.Dot(n, m))) * m;
Pointer.transform.position = intersectPoint;
}
}
ちなみに StartPoint にカプセルを、Plane にはプレーンを、Pointer にはスフィアを設定しています。