物理ベースのレンダリングについて調べているとよく出てくる「球面調和関数」。
今回はそれについて理解できたところ、忘れてまた調べたくなりそうなところをメモしていこうと思います。
ちなみに、ある程度理解がある人はこちらのt-potさんの記事(テイラー、フーリエ、球面調和関数)を見た方が理解が早いと思います。
概要
本記事は、学習のためにいくつかの数学的事実をメモ兼まとめとして記載したものです。
ちはみに数学に長けているわけではまったくなく、あくまで自分の理解と将来の自分へのメモなので 多分に間違いが含まれている可能性がある ことを先に断っておきます。
また、「球面調和関数」まわりを理解するために色々調べているので、それに近しいものをメインに扱っています。
そしてそれには、色々と単語周りが整理できていないと理解するのが大変なので、用語からメモしてます。
ちなみに結論から言うと、正直まだ全然分かってませんw なにかを期待して読み進めると後悔すると思うので先に書いておきますw
[2016.08.25追記]
色々情報もらったので追記。
級数とは
数学における級数 (きゅうすう、英: series) とは、ひと口に言えば数や関数など互いに足すことのできる数学的対象の列について考えられる無限項の和のことである。
そして、
級数を表す記法として、和記号 $∑$ を用いた表現 $∑ a_n$ や三点リーダ ⋯ を用いた表現 $a_0 + a_1 + ⋯$ などがある。
とあります。
要は なにかしら意味のある数字の集まりの和 ということですね。
下の「テイラー展開」などでも出てきますが、理解するイメージとしては「ある集まりの和」を「それがなにか」で意味付けするもの、と考えるといいかなと思います。
例えば、 $sin$ / $cos$ 関数をいくつか集めて、別の周期的な関数にすることを「フーリエ級数」と言ったりする、という具合です。
テイラー展開(テイラー級数展開)
テイラー展開(テイラーてんかい、英: Taylor expansion)とは、無限回微分可能関数 $f$ から、テイラー級数(テイラーきゅうすう、英: Taylor series)と呼ばれる冪級数を得ることを言う。名称は数学者ブルック・テイラーに由来する。
前述の級数の説明の通り、「意味のある数字のあつまりの和」が級数です。
そしてテイラー級数とは、「無限回微分可能関数から得たべき乗数の和」ということですね。
またWikipediaでは以下のような説明があります。
点 $a$ を含む開区間 $I ⊆ R$ 上で無限回微分可能な実数値関数 $f ∈ C^∞(I)$ が与えられたとき、べき級数
{\displaystyle \sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}}
>を関数 $f$ の点 $a$ まわりのテイラー級数という。
とあります。
さてここで、冒頭で紹介した[t-potさんの記事](http://t-pot.com/program/88_SH/)から画像を引用させていただいて、少し別視点からの話をします。
>ちなみに、 $sin(x)$ を最初の項から順に計算していくと、
>$y = x$、 $y = x - \frac{x^3}{3}$、 $y = x - \frac{x^3}{3!} + \frac{x^5}{5!}$
と、項が増えるに従ってだんだんとホントの値に近づいていくようすが見えます。
とあります。
↓画像
| $y = x$ | $y = x - \frac{x^3}{3}$ | $y = x - \frac{x^3}{3!} + \frac{x^5}{5!}$ |
|:--:|:--:|:--:|
|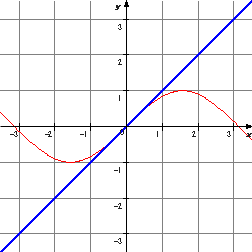|||
項が増えるに従って $sin(x)$ のグラフに近づいていくのが分かります。
「ある関数」のグラフの形状を、べき乗の総和(級数)で近似することができるというわけです。
つまり「べき乗の総和(級数)」を「ある関数のグラフに近似する」、という意味を与えている(そうなるようにしている)わけですね。
## 基底関数
>基底関数(きていかんすう、英: basis function)とは、関数空間の基底ベクトルのことである。すなわち対象となる空間に属する全ての元(関数)は、この基底関数の線型結合で表される。
[引用 Wikipedia](https://ja.wikipedia.org/wiki/%E5%9F%BA%E5%BA%95%E9%96%A2%E6%95%B0)
突然の基底関数の説明がなぜ入ったのかと言うとw
↑のテイラー展開で得られた級数はまさにこの「基底関数」が関係していると思います。(ここは「自分が」そういう理解している、という意味です;)
どういうことかというと、参考に載せた $sin(x)$ の関数に対して、べき級数で近似を行いました。
そしてそれは、足し込む項が増えるごとに精度があがっていくものでした。
よくみると、ひとつひとつの項が関数になっていて、それの実数倍を足しているのが分かります。
つまり、 **基底関数の線形結合で表されている** と言い換えることができます。
### 線形結合
>線型結合(せんけいけつごう、英: linear combination)は、線型代数学およびその関連分野で用いられる中心的な概念の一つで、平たく言えば、ベクトルの定数倍と加え合わせのことである。一次結合あるいは線型和とも呼ぶ。
[引用 Wikipedia](https://ja.wikipedia.org/wiki/%E7%B7%9A%E5%9E%8B%E7%B5%90%E5%90%88)
最初はなんのこっちゃ、と思いましたが、要はベースとなるベクトルを決めて、そのベクトルに対しての定数倍と、定数倍して得られたベクトルの組み合わせ「のみ」で表せられる集合、ということです。(ダメだ、うまく説明できない・・)
ちなみに **基底** の意味は以下のようです↓
### 基底
>線型代数学における基底(きてい、英: basis)は、線型独立なベクトルから成る集合で、そのベクトルの(有限個の)線型結合として、与えられたベクトル空間の全てのベクトルを表すことができるものを言う。もう少し緩やかな言い方をすれば、基底は(基底ベクトルに決まった順番が与えられたものとして)「座標系」を定めるようなベクトルの集合である[1]。硬い表現で言うならば、基底とは線型独立な生成系のことである。
>ベクトル空間に基底が与えられれば、その空間の元は必ず基底ベクトルの線型結合としてただ一通りに表すことができる。全てのベクトル空間は必ず基底を持つ(ただし、無限次元ベクトル空間に対しては、一般には選択公理が必要である)。また、一つのベクトル空間が有するどの基底も、必ず同じ決まった個数(濃度)のベクトルからなる。この決まった数を、そのベクトル空間の次元と呼ぶ。
[引用 Wikipedia](https://ja.wikipedia.org/wiki/%E5%9F%BA%E5%BA%95_(%E7%B7%9A%E5%9E%8B%E4%BB%A3%E6%95%B0%E5%AD%A6))
話を元に戻すと、様々あるグラフの形を上記の仕組みを持って近似し、高速に計算して「それっぽく」見せることとしたのがリアルタイムレンダリングでこうした概念が用いられる理由でしょう。
特に物理ベースの計算では様々な計算を行う必要がありますが、愚直にやっていては計算が追いつかない部分を、こうした近似によって求めている、というわけですね。
## 調和関数
球面調和関数の前に、調和関数についてメモ。というか引用。
>2つの実変数 $x ,y$ の実関数 $u(x,y)$ が,ある領域内で連続かつ1次および2次の偏導関数をもち,2次元のラプラスの方程式 $Δu=\frac{∂^2u}{∂x^2}+\frac{∂^2u}{∂y^2}=0$ を満たすとき,この関数 $u(x,y)$ はその領域において調和であるといい, $u(x,y)$ を調和関数と呼ぶ。
[引用 コトバンク](https://kotobank.jp/word/%E8%AA%BF%E5%92%8C%E9%96%A2%E6%95%B0-98246)
$x$ と $y$ の変化率の和が $0$ の場合に調和が取れている、ということ・・?
## ラプラス方程式
>ラプラス方程式(ラプラスほうていしき、英: Laplace's equation)は、2階線型の楕円型[偏微分方程式](https://ja.wikipedia.org/wiki/%E5%81%8F%E5%BE%AE%E5%88%86%E6%96%B9%E7%A8%8B%E5%BC%8F)
>
>
```math
∇2φ = Δφ = 0
である。ここで、 $∇2 = Δ$ はラプラシアン(ラプラス作用素、ラプラスの演算子)である。なお、 $∇$ についてはナブラを参照。ラプラス方程式は、発見者であるピエール=シモン・ラプラスから名づけられた。ラプラス方程式の解は、電磁気学、天文学、流体力学など自然科学の多くの分野で重要である。ラプラス方程式の解についての一般理論はポテンシャル理論という一つの分野となっている。
$R^3$ の場合に標準座標を用いてラプラス方程式を書くと次のようになる:
{\displaystyle {\partial ^{2} \over \partial x^{2}}\phi (x,y,z)+{\partial ^{2} \over \partial y^{2}}\phi (x,y,z)+{\partial ^{2} \over \partial z^{2}}\phi (x,y,z)=0.}
また別記事として△ [物理のかぎしっぽ]から、
勾配のそのまた発散を取ったものを ラプラシアン と呼び, $\triangle$ で表わします.式を読むときには,「デルタ」と読む場合もあります.
{\rm div (grad)}f = \nabla \cdot (\nabla f) = \triangle f
>
>記号でだけ考えれば, $\triangle$ は $\nabla$ の二乗(内積)と考えることも出来ます.
>
>```math
\nabla ^{2} = \nabla \cdot \nabla = \triangle = \frac{\partial ^2}{\partial x_{1}^{2}} + \frac{\partial ^2}{\partial x_{2}^{2}} + \frac{\partial ^2}{\partial x_{3}^{2}}
方程式としては、各要素に対して二階微分したものの合計が0になる、ということ・・?
偏微分方程式
偏微分方程式(へんびぶんほうていしき、英: partial differential equation, PDE)は、未知関数の偏微分を含む微分方程式である。
概要
微分方程式は通常多くの解を持ち、しばしば解集合を制限する境界条件を付加して考える。常微分方程式の場合にはそれぞれの解が幾つかのパラメータの値によって特徴付けられるような族を解に持っているが、偏微分方程式については、パラメータは関数値をとると考えるほうが有用である(砕けた言い方をすれば、これは解の集合がとても大きいということである)。このことは、ひどく過剰決定的な方程式系でない限りかなり一般に正しい。
偏微分方程式は、自然科学の分野で流体や重力場、電磁場といった場に関する自然現象を記述することにしばしば用いられる。
とりあえずざっくりと、自然科学で利用されるもの、そのあたりを表現するのに適しているもの、みたいな認識でしょうかね・・。
さて、球面調和関数からだいぶ離れましたがw
いよいよ、次は「球面調和関数」についてです。
球面調和関数
球面調和関数(きゅうめんちょうわかんすう、英: spherical harmonics[1])は、3次元のラプラス方程式の解を球座標で書いたときの角度部分の関数である。
球面調和関数 $Y_{\ell}^{m} (θ, φ)$ は、次の式で表される関数である。
{\displaystyle Y_{\ell}^{m}(\theta ,\phi )=(-1)^{(m+|m|)/2}{\sqrt {{\frac {2\ell +1}{4\pi }}{\frac {(\ell -|m|)!}{(\ell +|m|)!}},}}P_{\ell }^{|m|}(\cos \theta ),e^{im\phi }}
>ここで、 $ℓ$ は非負の整数、 $m$ は $−ℓ ≤ m ≤ ℓ$ の整数である。$P_ℓ^m$ はルジャンドル陪関数である。
>
>3次元のラプラス方程式の、球座標 $(r, θ, φ)$ による表式
>
>```math
{\displaystyle \nabla ^{2}u\equiv {\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial u}{\partial r}}\right)+{\frac {1}{r^{2}}}\left\{{\frac {1}{\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial u}{\partial \theta }}\right)+{\frac {1}{\sin ^{2}\theta }}{\frac {\partial ^{2}u}{\partial \phi ^{2}}}\right\}=0}
に対し、 $u (r, θ, φ) = R (r)Y (θ, φ)$ と変数分離してその分離定数を $λ$ とおくと、微分方程式
{\displaystyle {\frac {1}{\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial Y}{\partial \theta }}\right)+{\frac {1}{\sin ^{2}\theta }}{\frac {\partial ^{2}Y}{\partial \phi ^{2}}}+\lambda Y=0}
>が得られる。 $λ = ℓ (ℓ + 1)$ のときのこの方程式の解が、球面調和関数である。
なるほど、分からん。
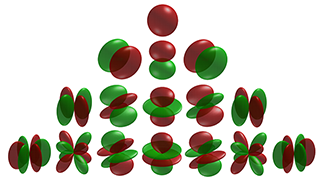
### 球面調和関数の具体例
ちなみにいくつかの具体例は以下のようになるようです。
```math
Y_{{0}}^{{0}}={\frac {1}{{\sqrt {4\pi }}}}
{\displaystyle Y_{1}^{0}={\sqrt {\frac {3}{4\pi }}}\cos \theta }
{\displaystyle Y_{1}^{\pm 1}=\mp {\sqrt {\frac {3}{8\pi }}}\sin \theta \,e^{\pm i\phi }}
{\displaystyle Y_{2}^{0}={\sqrt {\frac {5}{16\pi }}}(3\cos ^{2}\theta -1)}
{\displaystyle Y_{2}^{\pm 1}=\mp {\sqrt {\frac {15}{8\pi }}}\sin \theta \cos \theta \,e^{\pm i\phi }}
{\displaystyle Y_{2}^{\pm 2}={\sqrt {\frac {15}{32\pi }}}\sin ^{2}\theta \,e^{\pm 2i\phi }}
球面調和関数の説明には以下のような画像がよく添えられています。
この図、最初はなんのこっちゃ、でしたが、t-potさんの記事を引用させてもらうと、
とのこと。
電子が飛んでいる軌道を計算するのが球面調和関数。
で、それを物理ベースレンダリングで利用していると。
つまり、レンダリング対象の「とある点」に対する、周辺からの光の入り方などをある程度近似して計算してくれるものとして利用しているのでしょう。(という理解です、今のところ)
ちなみに直近で読んだ本によると、上記の具体例の範囲くらいの式で十分な精度が出るようです。
なので「使うだけ」なら、具体例を元に構築するのでもいいのかなと思っています。