とあるSlackのチャンネルでちょっと前に話されていたのを思い出して、メモとして残しておこうと思います。
(Three.jsのAdventCalendar(Three.jsでのクリッピング平面の利用)見てふと思い出したのでw)
概要
そもそも、OpenGLにはglClipPlaneという、クリッピング平面を指定する方法があるようです。
しかしWebGLではまだサポートされておらず、Three.jsではそれをフラグメントシェーダで行ってるよ、という会話があったのでそれの備忘録です。
※ ちなみに上記のSlackはこちら(webgl-jp)から参加することができます。興味がある方はぜひ!
Three.jsでの実装
どうやらフラグメントシェーダに以下のコードを追加することで対応しているようです。(by @technohippyさん)
# if NUM_CLIPPING_PLANES > 0
for ( int i = 0; i < NUM_CLIPPING_PLANES; ++ i ) {
vec4 plane = clippingPlanes[ i ];
if ( dot( vViewPosition, plane.xyz ) > plane.w ) discard;
}
# endif
大事なポイントは
if (dot(vViewPosition, plane.xyz) > plane.w) discard;
の部分です。
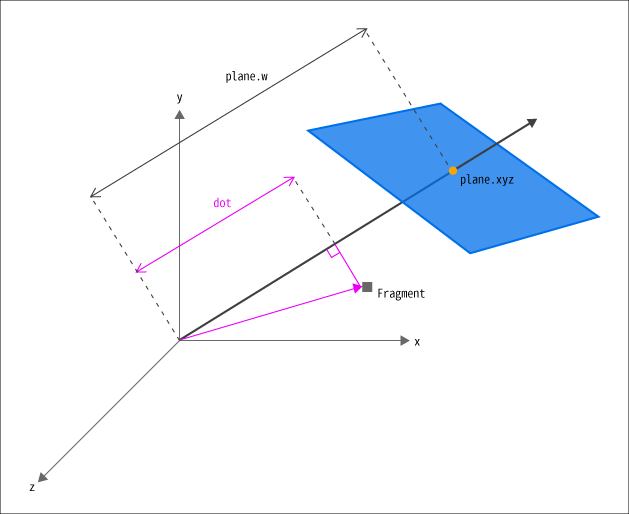
つまり、「フラグメントの位置と平面の位置ベクトルとの内積の結果」が「クリッピング平面のwの値」より大きい場合にフラグメントを破棄することで実現しています。
ちなみにそのときに@technohippyさんに図解してもらったのが以下の図です。
(今回用に清書しました)
※ ちなみに plane.xyz は「平面の方向」であり、実際の位置ではなく正規化された値が入っています。
Slackでの会話
Slackで @h_doxas さんがとても分かりやすく解説してくれたのでそれをメモとして残しておこうと思います。
以下、doxasさんとのやり取り。
doxas
半径10の球体があって
高さ5のところに、法線が Y 方向にまっすぐ向いている面がある
球体の北極点のところは、法線がやっぱり Y 方向にまっすぐ向いてる
北極部分の頂点座標と plane.xyz を内積で計算すると、計算結果は (0, 10, 0)
これと、plane.w に相当する 5 を比較してやるといい
edom18
さすがの解説力・・・!
doxas
つまり内積した結果と、面との距離とを比較することで、一定の面以上のきょりにあるかどうかわかるというわけ
なんとも分かりやすい・・!
ちなみになぜ plane.w と比較しているのかというと。
w の値はプロジェクション行列の計算で算出されます。
そしてその値はオブジェクトの z の値がそのまま格納されます。
(そして後の工程で w で割ることですべてのオブジェクトを 0 ~ 1 or -1 ~ 1 に正規化する同次座標系への変換に使われます)
なので図のように「内積を取り、その結果と w を比較する」ということは、そのままクリッピング平面との距離を比較している、というわけなのです。
そして結果として距離以上の(w より大きい)場合は平面を超えていることになるのでフラグメントを破棄している、というわけです。
それを踏まえて上の図を改めて見てみると、w の値がクリッピング平面との距離以上の場合に破棄するとクリップされることがよく分かると思います。