壁に平行なベクトルを求める
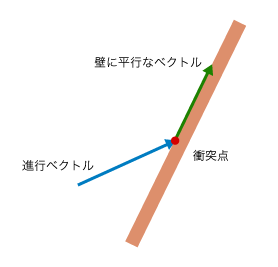
ゲームなどでは壁に体当りすると少し壁を登るように移動する場合がありますが、そうした状況で使えるベクトルです。
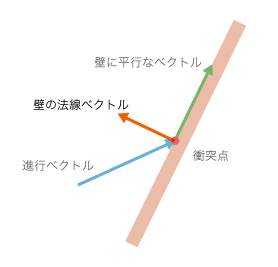
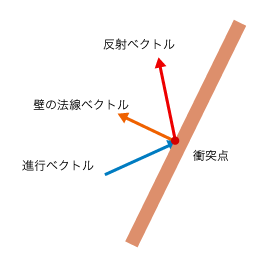
この「壁に平行なベクトル」を求めるのに必要なベクトルは、「進行ベクトル」と「衝突点に対する法線ベクトル」のふたつです。
計算を分かりやすくするためにベクトルを移動してみます。
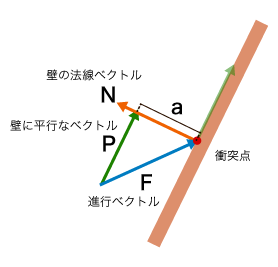
進行ベクトルを$F$、法線ベクトルを$N$、壁に平行なベクトルを$P$とすると、$P$は、$F$と、法線$N$に$a$を掛けた長さのベクトルを足したもの、ということが分かります。
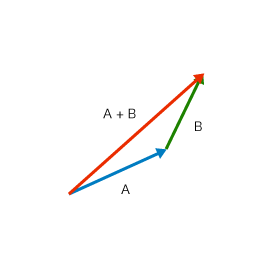
(余談)ベクトルの足し算
ベクトルの足し算は、一方の終点に他方の始点をあわせ、最初のベクトルの始点から、次のベクトルの終点へベクトルを伸ばしたものが結果として得られるベクトルです。
aを求める
ベクトル$F$、$N$は既知のものです。
この中で未知の値は$a$のみです。
$a$の値は内積を使うことで簡単に求めることができます。
(内積については前に記事を書いたのでこちらを参照)
$a$は進行ベクトルの逆ベクトルと法線ベクトルとの内積で求めます。
a = -F \cdot N
最終的に求めたいベクトル$P$は、求まった$a$を使って以下のように計算できます。
P = F + aN
展開すると、
P = F + (-F \cdot N)N
という式から、壁に平行なベクトルを求めることができます。
あとはこのベクトルに対して、進行ベクトルの強さや減衰率など、ゲームで必要な要素を加味して最終的に必要なベクトルを得れば完成です。
反射ベクトルを求める
反射ベクトルは以下のようなベクトルです。
実は壁に平行なベクトルを求めることができたら、ほぼ反射ベクトルは求まっています。
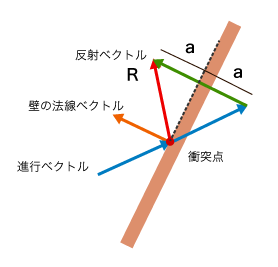
以下の図を見てください。
進行ベクトルの終点に、仮に反射ベクトルの始点を置いています。
また、進行ベクトルを衝突点から同じだけ進めたベクトルを追加しました。
図を見てもらうと分かりますが、進行ベクトルを方向を変えずに同じだけ進めると反射ベクトルの対象ベクトルが得られます。
あとは得られたベクトルを、反射方向に向きを変えられればいいわけです。
そして対象の中心となる面は当然、壁の法線が示す面となります。
前回求めた壁ずりベクトルはちょうどこの壁と平行になるベクトルでした。
そこで求めた係数は$a$ですね。
つまり、対象ということは同じだけベクトルを移動すれば対象のベクトルが得られます。
以上を式に表すと以下になります。
R = F + 2aN
壁と平行なベクトルは$P = F + aN$で求めていました。
この係数$a$を2倍にすることで目的の反射ベクトルが得られます。
これを展開すると以下となります。
R = F + 2(-F \cdot N)N
ひとつひとつ紐解いて行けば比較的単純に反射ベクトルを求めることができますね。