最近Unityをやり始めて、物理演算はほぼUnityがやってくれてほんと手軽。
一方で、それらがどういう仕組みで動作しているのかよくわかっていない。
ので、それだと気持ち悪いので色々と自分なりに勉強していく傍らで、備忘録と理解促進のためにメモを取っていくことにします。
※個人的な理解のために書いているのでところどころ間違っている可能性もあるのでご注意ください。
内積
内積とは、ふたつのベクトルの成す角に置いて以下の式を満たすもの。
Dot = A \cdot B = |A||B| \cos\theta \\
A \cdot B = (Ax * Bx) + (Ay * By) + (Az * Bz)
内積を使うことで得られるもの
計算により算出された値によってベクトルの位置関係を調べる
| 計算結果 | 意味 |
|---|---|
| 0以上 | 2つのベクトルが成す角は90度以内 |
| 0以下 | 2つのベクトルの成す角は90度以上 |
| 0 | 2つのベクトルは垂直(⊥) |
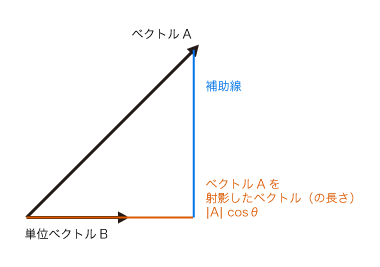
ベクトルを投影する
あるベクトル(A)をもうひとつのベクトル(B)に投影する。
投影は、ベクトルAの端点をベクトルBに垂直に下ろし、ベクトルBの始点と交差した点との長さを求める。
このとき、ベクトルBが単位化(長さが1のベクトル)されていた場合は、ベクトルAのベクトルB方向の長さ、となる。
図にすると以下のイメージ。
参考にした記事: ベクトルの小技
外積
外積は2次元と3次元で積の結果が異なる。
2次元の場合はスカラー積、3次元の場合はベクトル積となる。
2次元の外積
Cross = A \times B = |A||B| \sin\theta \\
A \times B = (Ax * By) - (Ay * Bx)
3次元の外積
\begin{equation}
A \times B
=
\begin{vmatrix}
(By * Az) - (Bz * Ay) \\
(Bz * Ax) - (Bx * Az) \\
(Bx * Ay) - (By * Ax)
\end{vmatrix}
\end{equation}
2次元の外積を使うことで得られるもの
計算により算出された値によってベクトルの位置関係を調べる
$A \times B$の場合
| 計算結果 | 意味 |
|---|---|
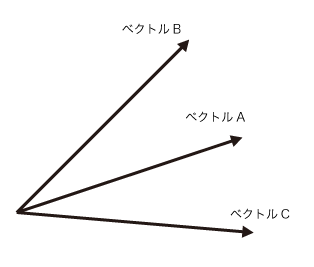
| 符号がプラス | ベクトルBはベクトルAの左側にある |
| 符号がマイナス | ベクトルBはベクトルAの右側にある |
| 0 | 2つのベクトルは平行 |
$A \times B$はプラス、$A \times C$はマイナスとなる
3次元の外積の意味
いつも外積の計算結果のベクトルの向きがどちらなのか、というのがぱっと出てこなかったんですが、この記事でやっと解決しました。
これによると、外積の向きは右手系と左手系で方向が逆になるようです。
OpenGLは右手系なので、その流れを組むWebGLは当然右手系です。
なので右手系で言うと、$A \times B$のベクトルの向きは、ABが作る平行四辺形の法線方向になります。
これは 右手 を使うことで分かりやすくなります。
右手の親指をAの方向に、人差し指をBの方向に向けたときに、それらに垂直になるように指を曲げた中指の向きが外積のベクトル方向となります。
自分はAB→C(親指から順番にベクトルを割り当てていく)という感じで覚えました。
ちなみに右手系は、親指をX軸方向に、人差し指をY軸方向にしたとき、中指が向く方向がZ軸の正の方向となる座標系です。
外積の行列表記
\begin{equation}
r \times q
=
\begin{vmatrix}
r_1q_2 - r_2q_1 \\
r_2q_0 - r_0q_2 \\
r_0q_1 - r_1q_0
\end{vmatrix}
=
\begin{vmatrix}
0 &-r_2 &r_1 \\
r_2 &0 &-r_0 \\
-r_1 &r_0 &0
\end{vmatrix}
\begin{vmatrix}
q_0 \\
q_1 \\
q_2
\end{vmatrix}
=
\tilde{r}q
\end{equation}
慣性テンソル
Wikipeidaによると、
角速度ベクトルと角運動量ベクトルが並行の場合は$I$はスカラーとなるが、一般の場合はテンソルとなり、 慣性テンソル と呼ぶ。
つまり、行列ってことかな?
慣性テンソルを式にすると
\begin{equation}
\begin{vmatrix}
L_x \\
L_y \\
L_z
\end{vmatrix}
=
\begin{vmatrix}
I_{xx} &-I_{xy} &-I_{xz}\\
-I_{yx} &-I_{yy} &-I_{yz}\\
-I_{zx} &-I_{zy} &I_{zz}
\end{vmatrix}
\begin{vmatrix}
\omega_x \\
\omega_y \\
\omega_z
\end{vmatrix}
\end{equation}
\\
L = 角運動量 \\
\omega = 角速度
微分・積分
力の関係を解決するのに、どうしても微積分は必須。ここはまだ理解が浅いので、徐々に拡充していきます。
微分
とある関数があり、そのどちらかの軸の(例えばX軸)方向に限りなく小さくした差分時点の接線の式。あるいは値。
微分でよく見る記号は「dx」や「⊿x」。
d = ⊿ = デルタと覚えておくといいかも。意味は「差分」。
位置の微分は速度なので、 $v = \frac{dx}{dt}$ 。
dtやdxは微分したよ、という意味のあくまで記号。
ちなみに二階微分の$\frac{d^2}{dx^2}$は、$\frac{d^2}{(dx)^2}$で、dxを二乗している。xの二乗ではない点に注意。
書籍から引用させてもらうと
三次元空間に存在する剛体の座標は(Xx, Xy, Xz)と表すことができる。座標の単位時間あたりの変化量は座標の時間微分であり、これが速度(Vx, Vy, Vz)である。この関係をそれぞれの次元に対する式にして表すと、以下のようになる。
\frac{d}{dt}Xx = Vx
\frac{d}{dt}Xy = Vy
\frac{d}{dt}Xz = Vz
速度ベクトル
これはX軸に対してのみの式なので、これをベクトル $X$ に置き換えると
\frac{dX}{dt} = V
という式が得られる。
加速度
さらに加速度はこの速度に対しての時間微分である。つまり、
\frac{dV}{dt} = a
となる。( $V$ は上で書いた速度ベクトル)
微分の公式
以下の式と例は§2 微分係数と導関数を参考にさせて頂きました。
関数$f(x)=x^2$を微分すると
$f'(x)=2x$
関数$f(x)=x^3$を微分すると
$f'(x)=3x^2$
関数$f(x)=x^4$を微分すると
$f'(x)=4x^3$
関数$f(x)=x^5$を微分すると
$f'(x)=5x^4$
このとき、$f'(x) = 5x^4$などは「導関数」と呼ぶ。
$f(x) = x^2 - 3x + 4$について、$f'(a)$の一般式として解いてみる。
\begin{equation}
f'(a) =
\lim_{h \to 0} \frac{f(a + h) - f(a)}{h} \\
=
\lim_{h \to 0} \frac{\{(a + h)^2 - 3(a + h) + 4\} - \{a^2 - 3a + 4\}}{h} \\
=
\lim_{h \to 0} (2a - h - 3) = 2a - 3
\end{equation}
この式の$a$を$x$に置き換えると、$f(x) = x^2 - 3x + 4$の導関数は$2x - 3$となる。
ニュートンの法則
今回は物理演算的なことやっているので、加速度からさらに物体に働く力を求める必要がある。一般的に小さいものほど小さい力で動かせる。つまり物体に働く力とそれによって生じる加速度は比例関係にある。
この力 $f$ と加速度 $a$ を式に表すと
f = ma
ここで $m$ はその物体の質量を表す。(小さいものほど必要な力 $f$ が小さくなる)
質量
ちなみに質量の求め方を書籍から引用すると
質量 $m$ とは物体の密度 $p(x)$ を空間積分したものと定義される
密度が物体内で一定であると仮定すると式はとてもシンプルになり、
m = νρ
となる。(ここでは $ν$ は体積、 $ρ$ は密度)
積分
積分の表し方
\int f(x) dx = F(x) + C = G(x)
とするとき、2つの実数a, bに対し、$G(b) - G(a)$ (グラフのaからbの積分)の値を考えてみる。
$G(x) = F(x) + C$ であるから、
G(b) - G(a) = \{F(b) + C\} - \{F(a) + C\} = F(b) - F(a)
となる。この $F(b) - F(a)$ を $y = f(x)$ の a から b までの定積分という。
ちなみに定積分の式を以下のようにも書ける。
\int_2^5 x^n dx = \left[\frac{1}{n+1}x^{n+1}\right]_2^5
多重積分
積分をさらに積分する「多重積分」というのがあります。
\int \!\!\!\!\! \int f(x, y) dx dy
というような形のものです。
この計算についてはこちらの記事が分かりやすかったです。
上記記事から引用させてもらうと、
関数 f(x, y) の y を定数とみなして x について積分したものである。 その結果は一般に変数 y を含むから、 yの関数になる。 この関数を g(y) とおくと
\int_c^d \!\!\!\!\! \int_a^b f(x, y) dxdy \\
= \int_a^b g(y) dy
が求める 2重積分となる。また x と y の順序を交換しても同様である。
このように、 1つの変数に関して積分した結果をさらに他の変数に関して積分することを累次積分という。
とのこと。
実際に計算すると以下のようになります。(引用です)
関数 f(x, y) = x+y の領域 K (0 ≦ x ≦ 1, 1 ≦ y ≦ 2) における重積分は
\int \!\!\!\!\! \int_K f(x, y) dxdy \\
= \int_1^2 \!\!\!\!\! \int_0^1 (x + y) dxdy \\
= \int_1^2 \left[\frac{1}{2}x^2 + yx\right]_0^1 dy \\
= \int_1^2 \left(\frac{1}{2} + y\right) dy \\
= \left[\frac{y}{2} + \frac{y^2}{2}\right]_1^2 \\
= (1 + 2) - (\frac{1}{2} + \frac{1}{2} \\
= 2