射影テクスチャリングはテクスチャを、プロジェクタで写し出したように投影して表示するものです。
詳細についてはこちらを参考(射影テクスチャリング)に。
この手法は様々なものに応用されており、例えばシャドウマッピングなどにも利用されています。
ということで、覚えておかなければならないスキルだと思うので色々とメモしておこうと思います。
ちなみにWebGLで使うにはこちらの記事(射影テクスチャマッピング | wgld)がとても参考になります。
注意点
射影テクスチャマッピングを行うにあたり、テクスチャ周りについて詳しく知っておかなければなりません。
その中の注意点として、OpenGLでは通常テクスチャ座標系は 左下 が原点です。
一方、通常の画像は 左上 が原点ですね。
このことからも考慮しなければならないことがあるのが分かるかと思います。
座標系を把握する
さて、上記以外にも座標系として注意する点があります。
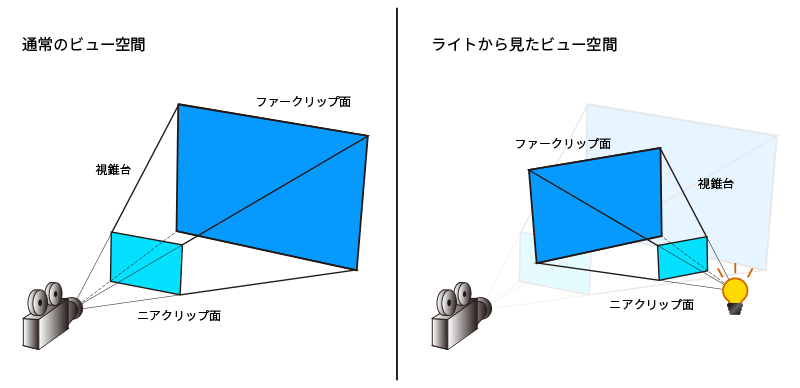
それは主題である「射影」についてです。
これは通常のビュー変換と同じように、ライトから見た「透視変換行列」を作る必要があります。
さて透視変換行列ですが、これの座標系の中心(要は「0, 0」)は「中央」です。
座標系が異なるのがまた出てきました。
まとめると、
- 画像座標空間
- テクスチャ座標空間
- 射影座標空間
の3つ、それぞれが異なることになります。
これを適切に扱えるように変換する必要があります。
射影空間からテクスチャ座標空間に変換する式は、
S = 0.5X + 0.5 \\
T = 0.5Y + 0.5
となります。(射影空間の(0, 0)がテクスチャ座標空間の(0.5, 0.5)になるように変換する)
ただこのままだと上下の反転がそのままです。
判定するには、単にY座標をマイナスしてやればいいですね。
つまり、
S = +0.5X + 0.5 \\
T = -0.5Y + 0.5
となります。
ただ、これだと射影空間上のZ値が反映されていません。
(Wで除算されていない。つまり w=1 のときの状態)
そのため、正確な情報は以下のようになります。
S = +0.5\frac{x}{w} + 0.5 \\
T = -0.5\frac{y}{w} + 0.5
さらに$0.5$でまとめて
S = 0.5\frac{w + x}{w} \\
T = 0.5\frac{y - w}{w}
となります。
計算しやすいように行列の形にしておきましょう。
行列の形にすると以下のようになります。
\begin{equation}
\begin{vmatrix}
s \\
t \\
? \\
w
\end{vmatrix}
=
\begin{vmatrix}
0.5 &0 &0 &0.5 \\
0 &-0.5 &0 &0.5 \\
0 &0 &1 &0 \\
0 &0 &0 &1
\end{vmatrix}
\begin{vmatrix}
x \\
y \\
z \\
w
\end{vmatrix}
\end{equation}
最後に、この射影テクスチャを利用するための最終結果を求める行列計算は以下のようになります。
行列をどう使うか
さて、上記までで必要な座標変換の行列は求まりました。
が、実際にこれをどう使ったらいいでしょうか。
求めた行列の意味は「ライトから見た透視投影変換」に、テクスチャ座標変換行列を掛けたものでした。
これはどういう意味なのか。
GLSL にはtexture2Dという、テクスチャのピクセル(テクセル)から色をフェッチするビルトイン関数があります。
この関数は2次元のテクスチャからUV座標を元にテクセルを取得するものです。
これと似たような関数にtexture2DProjという関数があります。
この関数はふたつの引数を取り、それぞれテクスチャと3次元座標を取ります。
// x, y, z, wはフェッチしたい座標
vec4 sampleColor = texture2DProj(texture, vec4(x, y, z, w));
こちらはProjという名前から推測できるように、上記で求めた透視投影変換した座標からテクスチャのテクセルをフェッチする関数です。
自分のイメージでは金太郎飴ですw
↓こんな感じ。
こうして、第二引数で渡された座標位置にあるテクセルを取得し、それをレンダリングに使う、というわけです。
仕組みを理解してしまえばそれほどむずかしいものではありません。
また、この仕組みを応用して、冒頭でも書いたように「シャドウマップ」という方法で影をレンダリングする方法もあります。
なぜ「シャドウマップ」というのかはイメージできるのではないかと思います。
シャドウマップもやってみようと思うので、やったら記事を書きたいと思います。