以前、「[Unity] ファーシェーダを移植してみた」という記事でファーシェーダについて書きました。
今回は、1枚の毛皮画像から深度を推測し、もっと毛皮らしい見た目にするテクニックです。
こちらの記事([CEDEC 2012]毛皮表現用プロシージャルテクスチャ生成技法はモフモフウサギの夢を見るか? 「実写画像を用いたShell Texture自動生成手法」)を参考にしました。
実写の毛皮から計算してテクスチャを得る
この1枚の毛皮写真だけを使ってレンダリングしたのが以下のものです。

以前紹介したテクニックではファーの長さがすべて均一に伸びていましたが、こちらは明るいところと暗いところで微妙に長さが異なり、より毛皮らしい雰囲気になっているのが分かるかと思います。
理論
参考にした記事で発表された内容は、「毛皮の写真の輝度から深度を推測するもの」、と言うことができます。
毛は幾重にも重なって複雑な陰影を持ちますが、この陰影を、簡易的なモデル化を行うことで毛の層の深さを測ろう、というものです。(と理解してます)
余談
ちなみに、しっかりとしたファーをレンダリングする場合は、事前に毛の断面図を何枚も作成し、それを毛の深度に応じて使い分けながらリアルなファーを表現するようです。
ただ当然、そのテクスチャを準備するのは大変です。
しかし今回のテクニックは「1枚の写真から実行時に断面図のテクスチャを生成してしまおう」というのが基本的な考え方です。
深度と輝度の相関
まず、写真の情報とは別に深度によってどれくらい輝度が減衰するのかを以下の式を用いて計算します。
以下の式で利用している写真の情報は、写真内の 最低輝度(Imin) と 最大輝度(Imax) です。
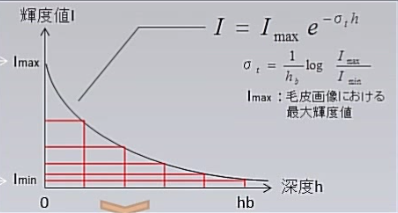
(出典 : [CEDEC 2012]毛皮表現用プロシージャルテクスチャ生成技法はモフモフウサギの夢を見るか? 「実写画像を用いたShell Texture自動生成手法」)
図は縦に輝度値、横に深度を取ったグラフです。
(深度に対してどれくらい輝度が減衰していくかを示しています)
横軸の一番右、hbと書かれているところが一番深いところ、一番左が一番表面、ということになります。
なので、0のときはImax、hbのときはIminと等しいグラフになっているわけですね。
そして右上には数式が書かれています。これがこのグラフの曲線を表す式です。
表面から深くになるにつれて、指数関数的に輝度が減衰しているのが分かると思います。
これをプログラムにしたのが以下です。
var hb = 5.0; // 毛の深さ
var k = Math.log(max/min) / hb // 係数。σの部分。
var h = (n/N * hb); // nは現在計算中のファーの層、Nはファーの最大積層数
var result = max * Math.exp(-k * h);
kが図のσです。
n/Nはファーの積層数と、現在計算中の層を意味しています。(例えば60層で30層目なら30/60 = 0.5となる)
この計算の意味はグラフの通り、h = 0でI == Imax、h = hbでI == Iminとなることを意味しています。
この式がどういう値を返すかを調べるためのサンプルを作ったので、どういう値になるのか興味ある人は見てみてください。
動的に毛皮断面のテクスチャを生成する?

(出典 : [CEDEC 2012]毛皮表現用プロシージャルテクスチャ生成技法はモフモフウサギの夢を見るか? 「実写画像を用いたShell Texture自動生成手法」)
動画のキャプチャですが、動的にテクスチャを計算する方法が紹介されている箇所です。
これは計算中の層に対するテクスチャの状態を計算するためのものです。
(例えば30層目なら30層目としてのテクスチャを得る)
d1とd2がなにを意味しているか、というと、以下の図を表しているのだと思います。
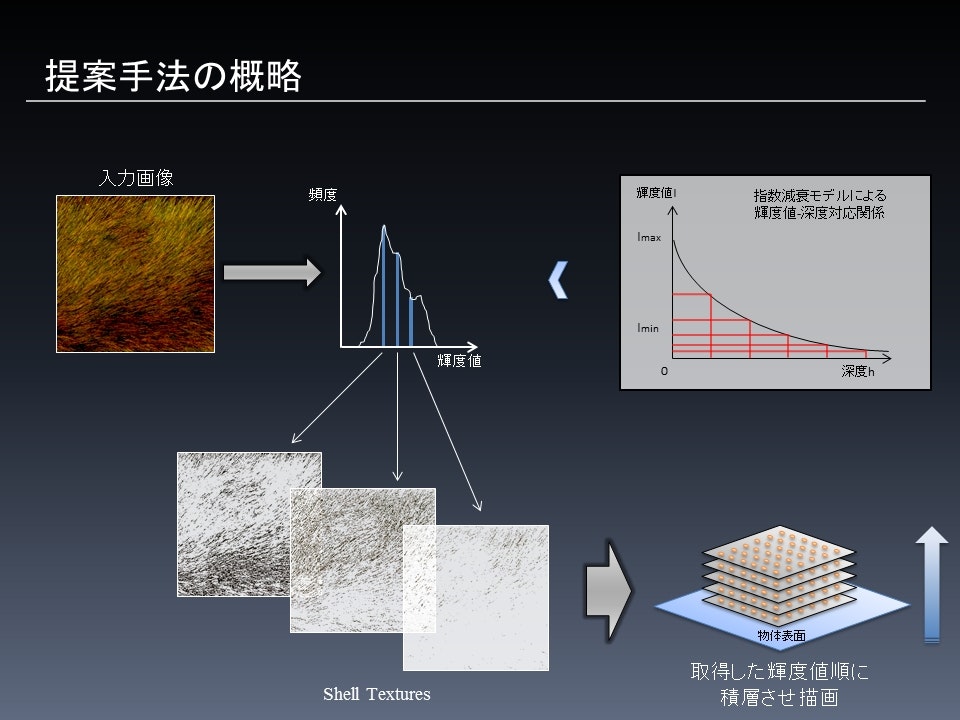
(出典 : [CEDEC 2012]毛皮表現用プロシージャルテクスチャ生成技法はモフモフウサギの夢を見るか? 「実写画像を用いたShell Texture自動生成手法」)
ただ、ここでいうd1とd2を算出する式が分からず、とりあえず以下のようにしたらそれっぽい感じになりました。( なので、こうやるんだよっていうのが分かる人いたらコメントください; )
該当テクスチャを得る
テクセルに対してd1を最低レベル、d2を最大レベルになるようレベル補正を行った上で、輝度相関グラフの輝度値と比較して、相関グラフから求めた輝度値のほうが大きい場合にテクセルをレンダリングする、という方法で計算してみました。
その計算で得た結果が、冒頭のキャプチャです。
サンプルコード
上記を元に書いたコードの抜粋が以下です。
テクセルの計算と輝度値の比較部分までを載せています。
const int totalLayer = 60;
const float unit = (float)(1.0 / totalLayer);
const float3 perception = float3(0.298912, 0.586611, 0.114477);
// Caluculate luminance from offset.
float hb = _FurLength;
float k = log(_IMax/_IMin) / hb;
float I = _IMax * exp(-k * ((1.0 - FUR_OFFSET) * hb));
float min = saturate(unit * (LAYER - 1));
float max = saturate(unit * LAYER);
float ratio = 1.0 / (max - min);
float4 lumpx = tex2D(_MainTex, i.uv);
////////////////////////////////////////////////////////
// RED
if (lumpx.r < min) {
lumpx.r = 0.0;
}
else if (lumpx.r > max) {
lumpx.r = 1.0;
}
else {
lumpx.r = (lumpx.r - min) * ratio;
}
////////////////////////////////////////////////////////
// GREEN
if (lumpx.g < min) {
lumpx.g = 0.0;
}
else if (lumpx.g > max) {
lumpx.g = 1.0;
}
else {
lumpx.g = (lumpx.g - min) * ratio;
}
////////////////////////////////////////////////////////
// BLUE
if (lumpx.b < min) {
lumpx.b = 0.0;
}
else if (lumpx.b > max) {
lumpx.b = 1.0;
}
else {
lumpx.b = (lumpx.b - min) * ratio;
}
float luminance = dot(lumpx.rgb, perception);
if (luminance < I) {
discard;
}
[2014/11/16 追記]
上記のd1、d2についてもう少し理解が進んだので追記。
diは書かれたままの意味でした。つまり輝度区分のインデックスです。
d0を最低輝度(Imin)、dNを最大輝度(Imax)とし、その間を任意の数Nで分割します。
(Nはファーの積層数)
例えば、d0 = 0.1、dN = 0.9とした場合、d3は以下の式で求まります。
var N = 10;
var Imin = 0.1;
var Imax = 0.9;
var dist = (Imax - Imin) / N;
var d3 = (dist * 3) + Imin; // => 0.34
輝度値区分内のテクセルのみ利用
これでdiの値が求まります。
そして仮にd1〜d2の範囲の輝度を持つテクセルを取得したい場合は、
// 擬似プログラム的に書いています
if (d1 <= getPixel(x, y) <= d2) { // ピクセルはグレースケール化済とします
// draw texel.
}
else {
// discard texel.
}
として判断が可能です。
視覚的に分かりやすくするためのデモを作りました。
左右のつまみ(▲)をドラッグすると、輝度範囲の最小と最大を操作できます。
感想
ただ、上記は理解できたものの、実際にこれをファーとして設定するとファーの点がとびとびになってしまって毛っぽくなくなってしまいました。(まだ他にもなにか考慮しなければならないんだと思います)
ただ、輝度値の区分として下端(上記で言えばd1)の値以下はレンダリングしないとしたところそれっぽくなりました。
(つまり<= d2を外した)


