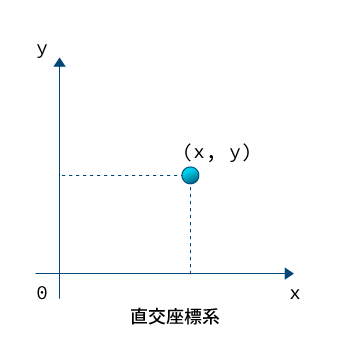
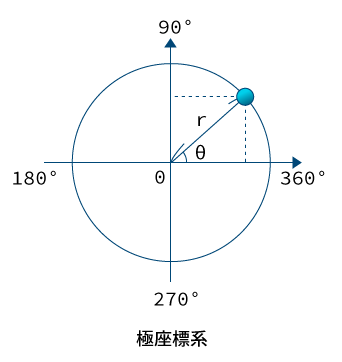
概要
考え方として、「直交座標の点を極座標に置き換える」のではなく、「極座標の任意の点は直交座標のどの点か?」を考えます。
(そうしないと隙間が空いてしまう)
一般的に、数学で考えるときは上のような座標系で値の取り方が決まっているようです。
- 極座標の中心からの角度($θ$)を直交座標のX座標
- 極座標の中心からの距離($r$)を直交座標のY座標
とします。
一般的には、
$$\theta = X * \frac{360}{width}$$
で求めるようです。
そして直交座標系の$Y$がそのまま$r$に対応します。
変換のイメージ
実際にチェックの画像を用いて見てみるとイメージしやすいと思います。
以下は、実際にUnityで座標変換したものをテクスチャにして貼り付けた例です。

Y軸とrのイメージ
左が直交座標系でのテクスチャ、右が極座標系でのテクスチャです。
イメージの仕方としては、仮に$X$の値が$0$に固定したことを想像してみてください。
そののち、$Y$軸の値だけを変えると白黒白黒・・・と変化していくことがイメージできるかと思います。
そして、極座標ではその$Y$軸の変化を$r$に割り当てるので、結果として同心円状に色が変化していくことになります。
それを想像しながら左右の絵を見てみると、右の同心円状に色が変化しているのと左のチェックの色が対応しているのがイメージできると思います。
X軸とθのイメージ
今度は逆に、$Y$軸の値を$0$に固定して考えてみます。
$X$軸の値が変化する、つまり左右に色が変化していきます。
模様は同じなので変化は黒白黒白・・・となるのは同じです。
そして$X$の値が変化すると、対応する極座標では$θ$の値となって現れるわけです。
つまり、先程の同心円状の上を点が移動するイメージですね。
なので、冒頭の式としてそれぞれ、XとYが$θ$と$r$にマッピングされる、というわけです。
イメージができてしまえば対して難しい処理ではないことが分かるかと思います。
プログラムでの実装
しかし、実際のプログラムでの実装では以下のように考えます。
- $\theta$から$X$を求め、
- $r$から$Y$を求める
さらに、極座標をプロットといっても、実際プロットする先は$XY$直交座標系になります。
実際、テクスチャなどはUV座標系で扱うため、$XY$直交座標で表されていないと都合が悪いですよね。
ということで、とある$X, Y$の点から角度と原点からの距離を求めます。
r(原点からの距離)を求める
原点からの距離は(x, y)の値から距離を求める公式で簡単に求めることができますね。
具体的には以下です。
$$
r = \sqrt{X^2 + Y^2}
$$
θを求める
次に、($x, y$)の値から角度を求めます。
角度はアークタンジェントを使えばすぐに分かります。
$$
\theta = \arctan\left(\frac{Y}{X}\right)
$$
ここから、$X, Y$を求める式に直すと、
$$
Y = \sqrt{x^2 + y^2}
$$
$Y$はシンプルですね。$r$の値がそのままYにマッピングされるので、左辺が$Y$になったのみです。
$$
X = \arctan\left(\frac{y}{x}\right) * \frac{width}{360} * \frac{180}{\pi}
$$
$X$はやや複雑ですが、冷静に考えればそこまで難しくはありません。
まず、右辺の最後の項はたんにradianからdegreeに変換しているだけです。
右辺の真ん中は、$width$倍したあとに$360$で割っています。
アークタンジェントの値はただの比率なので、それを幅にかけているわけですね。
そして360で割っているのは、$X$軸は$θ$の値を使うので、一周$360°$で割ることで周期を作り出しているわけです。
先ほどの図のイメージと合わせて考えて見ると想像しやすいと思います。
そして、極座標で表された絵を$XY$直交座標にマッピングすると、冒頭の図のような絵になる、というわけです。
すでに書いた通り、テクスチャなど平面で見るのには$XY$直交座標でないと都合が悪いので、計算して求めたピクセルの色を$XY$直交座標にマッピングしなおしている、というわけですね。
サンプルコード
通常のテクスチャからGetPixelsして得たColor[]を元に、極座標に変換するコード例です。
private void Convert(Color[] colors, int width, int height)
{
int halfWidth = width / 2;
int halfHeight = height / 2;
Texture2D tex = new Texture2D(width, height);
Color[] newColors = new Color[colors.Length];
GameObject quad = GameObject.CreatePrimitive(PrimitiveType.Quad);
quad.name = "PolarCoord";
for (int y = 0; y < height; y++)
{
for (int x = 0; x < width; x++)
{
int dx = x - halfWidth;
int dy = halfHeight - y;
int X = (int)Mathf.Floor(Mathf.Atan2(dy, dx) * (width / 360f) * (180f / Mathf.PI));
int Y = (int)Mathf.Floor(Mathf.Sqrt(dx * dx + dy * dy));
int idx = (Y * width) + X;
Color color = colors[idx];
int newIdx = (y * width) + x;
newColors[newIdx] = color;
}
}
tex.SetPixels(newColors);
tex.Apply();
Renderer ren = quad.GetComponent<Renderer>();
ren.material.mainTexture = tex;
}
これを実行して表示たのが冒頭のキャプチャ画像です。