概要
理解した気になっているパースペクティブ射影変換行列。
今回はそれを、とあるSlackで質問させてもらってある程度理解が進んだのでそれのメモです。
ちなみに、マルペケさんの記事(その70 完全ホワイトボックスなパースペクティブ射影変換行列)が「なにをしているのか」を理解するのにとてもオススメです。
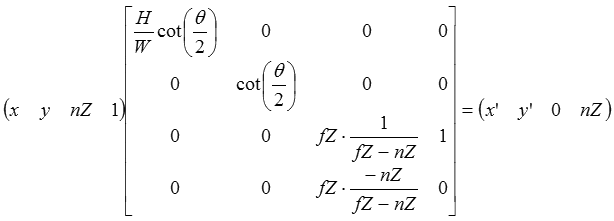
最終的な行列の形は以下。(画像を引用させていただいています)
異なるパースペクティブ射影変換行列
さて、パースペクティブ射影変換行列を調べているといくつかの「形」があることに気づきます。
今回はそれのメモです。
具体的には、Three.jsなどでは以下のようにパースペクティブ行列を作っています。
makePerspective: function ( left, right, top, bottom, near, far ) {
if ( far === undefined ) {
console.warn( 'THREE.Matrix4: .makePerspective() has been redefined and has a new signature. Please check the docs.' );
}
var te = this.elements;
var x = 2 * near / ( right - left );
var y = 2 * near / ( top - bottom );
var a = ( right + left ) / ( right - left );
var b = ( top + bottom ) / ( top - bottom );
var c = - ( far + near ) / ( far - near );
var d = - 2 * far * near / ( far - near );
te[ 0 ] = x; te[ 4 ] = 0; te[ 8 ] = a; te[ 12 ] = 0;
te[ 1 ] = 0; te[ 5 ] = y; te[ 9 ] = b; te[ 13 ] = 0;
te[ 2 ] = 0; te[ 6 ] = 0; te[ 10 ] = c; te[ 14 ] = d;
te[ 3 ] = 0; te[ 7 ] = 0; te[ 11 ] = - 1; te[ 15 ] = 0;
return this;
},
これについて、「なぜ形が違うのだろう」とずっと疑問に思っていて、とあるSlackで質問して回答をいただいたのでそのメモです。
そのときの回答を、本人の許諾をいただいて引用させていただきました。
x軸とy軸の部分の差は、上に書かれているのは方法z軸方向を画面中心として
縦方向の角度Θに限定した時の計算で、展開すればやっていることは下の物と同じです。
y軸の計算だと
cot(Θ/2) = n / (H / 2)
= 2 * n / H
= 下の式
下の方法は柔軟ですが、大体のカメラは上の方法で問題ないです。
z軸の計算方法が違うのは、上の方法はDirectXのViewport座標系0.0~1.0になるように計算しているのと、
下の方法がOpenGLのViewport座標系-1.0~1.0になるように計算しているのが違います。
あとはカメラの奥方向が+zか-zかが違います。
これは右手系か左手系かの違いというのが大きいと思います。
まず、$cot\bigl(\frac{\theta}{2}\bigr)$は$\frac{1}{tan(\frac{\theta}{2})}$です。
$tan(\theta)$は$\frac{対辺の長さ}{隣辺の長さ}$で表されます。(参考:直角三角形の各辺の名称)
つまり、$cot(\theta)$はその逆数になっているので、$\frac{隣辺の長さ}{対辺の長さ}$となりますね。
対辺の長さは、上の式で言うと$\frac{H}{2}$ (H = height)に相当します。
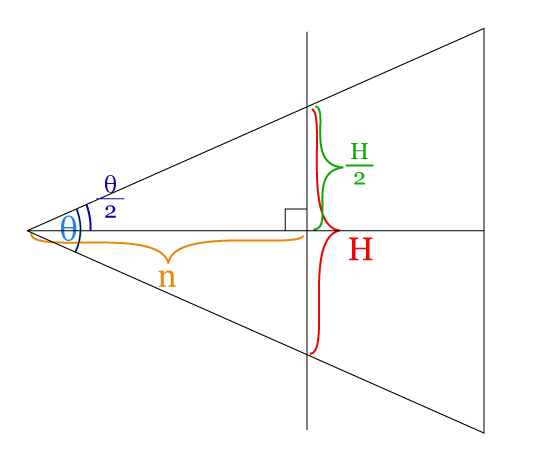
さて、この対辺の長さなどの値の根拠ですが、図にすると以下のようになります。
もともと、fov(Field of View)は視錐台の角度を表すものです。
意味は上図の通りです。(上図は視錐台を真横から見たものと思ってください)
角度$\theta$は視錐台の角度です。そしてちょうど半分の$\frac{\theta}{2}$が直角三角形の角度となることも分かります。
この直角三角形をふたつ合わせた対辺の合計が視錐台の高さ(height)に相当するため、前述の式のようにその半分となる$\frac{H}{2}$が算出されます。
結果として上式が導かれる、というわけです。
冒頭の図ではx、yともに$cot\bigl(\frac{\theta}{2}\bigr)$が指定されていますが、それぞれ縦横(width, height)の計算となります。(なので実質同じ計算)
続く後半の部分の説明は、「正規化デバイス座標系」と「右手系・左手系」の違いによる計算の違いについて説明されています。
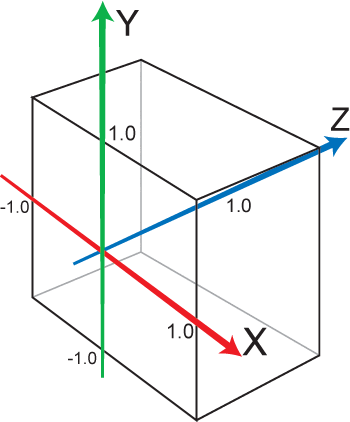
まず、正規化デバイス座標系ですが、冒頭のマルペケさんのサイトから図を引用させていただくと以下のようなものを指します。
「正規化」と名前がつく通り、3D空間を-1.0〜1.0の間にぎゅーっと濃縮された空間を表しているのが分かるかと思います。
要は、レンダリング対象となる視錐台を-1.0〜1.0の範囲に圧縮し立方体の形に変形した、というわけです。
このことを踏まえて冒頭の計算式を見てみると、$(far - near)$で除算しているのが分かります。
これはつまりはカメラが撮影できる範囲(nearからfarの距離)を計算し、それで割ることでZ軸方向を0.0~1.0の「正規化」しているというわけなんですね。
さて、X,Y軸は-1.0~1.0だったのに対し、なぜZ軸は0.0~1.0なのでしょうか。
ここでDirectXとOpenGLで違いがあります。
それが
DirectXのViewport座標系0.0~1.0になるように計算しているのと、
下の方法がOpenGLのViewport座標系-1.0~1.0になるように計算しているのが違います。
の部分ですね。
これは単に取り決めの問題です。ひとつのプラットフォームで作っている場合は特に意識する必要はありませんが、クロスプラットフォームなものを作る場合は違いがあることを知っておかないとなりません。
そのための計算違いが図とコードでの差、というわけです。
最後は右手・左手座標系での違いです。
これは単に、Z軸のプラス方向がどちらを向くのか、ということです。
左手座標系だとZ軸プラスはカメラの視点方向に移動することになります。(つまりプラス方向に移動するとカメラから遠ざかっていく)
逆に右手系はその逆となるので、プラス方向に移動するとカメラに近づいてくるようになります。
この違いを表しているのがte[ 11 ] = - 1;で表されている部分です。
この1が入っている詳細はマルペケさんの記事を見ていただくとして、ここがマイナスになることでZ軸の方向が反転され、以下のことが実現している、というわけです。
あとはカメラの奥方向が+zか-zかが違います。
ちなみにここは自分の推測ですが、cの計算部分。
var c = - ( far + near ) / ( far - near );
最初、なぜ+ nearなんだろう、と思ったのですが、ここ、座標変換中の値のz値がnearとイコールの場合は(DirectXの場合は)0となる計算です。
ところが、OpenGLでは-1.0~1.0で計算を行うため、最終的に残ってほしい値はnearの値です。
なので、+ nearなのかな、という理解です。
(もし違っていたら誰か指摘ください( ;´Д`))
a と b の値の意味(推測)
上記行列の計算で a と b の値が計算されています。以下の部分ですね。
var a = ( right + left ) / ( right - left );
var b = ( top + bottom ) / ( top - bottom );
上下左右の計算なので、X軸に対する計算かY軸に対する計算か、の違いだけなので a に絞って考えてみます。
まず、視錐台は通常、原点に対して左右(上下)対称です。つまり、 left と right は正負が逆で同じ値が格納されることになります。なので上記の計算は相殺が起こります。例えば left = -100 right = 100 と考えた場合、
(right + left) = (100 + (-100)) = 0
となって結果は常に 0 になります。
視錐台が歪むと a と b の値が変化する
さてではどういうときに 0 以外になるのでしょうか。答えは、視錐台が歪んだとき、つまり左右(上下)対称でなくなったとき、です。これまた例として left = -90 right = 100 と考えた場合、
(right + left) = (100 + (-90)) = 10
となりますね。なので歪みの意味を持たせている、というのが自分の理解です。
とにもかくにも、パースペクティブ射影変換行列は複雑ですね。
でもおかげでだいぶ頭の中が整理できました。
改めて、マルペケさんとSlackで回答していただいた方に感謝です。