[3D] 三角形と線分の交差判定（Raycast）

いわゆる Raycast ですね。
線分が三角形、つまりポリゴンと交差しているかを判定することで、例えば3D空間上のオブジェクトをマウスで選択したり、あるいはオブジェクトが接触しているか、などなど様々な判定をすることができます。

今回はこの「三角形と線分との交差判定」について調べてみたのでそのメモです。

理論

今回参考にしたのは「Tomas Mollerのアルゴリズム」です。比較的高速で一般的な手法のようです。
概要についてはこちらの記事を参考にしました。

なにを求める？

各式や、計算方法などは見ていればなんとなく分かりますが、これがなにを求めているのかが最初は分かりませんでした。
行っていることは最終的にはごく簡単な1次関数のグラフに落としこむものでした。
具体的には以下の画像を見てください。

考え方

レイをある方向に飛ばします。
仮にこのレイが三角形面と交わると仮定します。
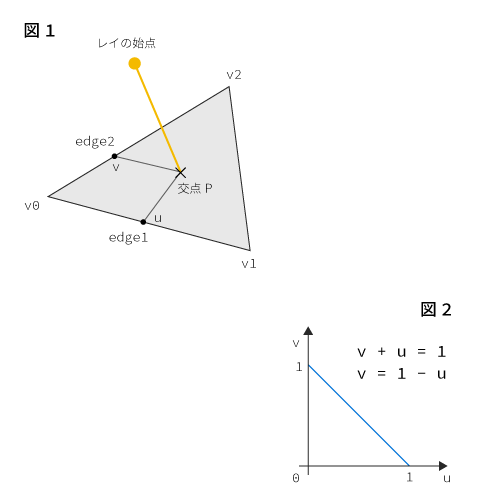
すると上記の図1で示したように、三角形の頂点のうちのひとつ（上記例では v0 ）から、edge1およびedge2にそれぞれ u と v という係数を掛けたベクトルを足すことで算出することができます。

そしてこれを図2のグラフとして見てみると、グラフの線と uv 軸で囲まれた領域の中に交点があることになります。
逆に言うとu（あるいは v） が 1 を超えた場合、領域外に出てしまうことが分かるかと思います。

つまり、u と v は 1 を超えてはならず、さらにグラフが示すところによると u + v の値も 1 を超えてはならないことが分かります。

式にすると、

0 ≦ u ≦ 1 \\
0 ≦ v ≦ 1 \\
0 ≦ u + v ≦ 1

という関係が成り立ちます。
今回のこの理論はこれらを、与えられたレイの情報と、三角形の3頂点の情報から導き出す、というものになります。

計算

計算については、冒頭の記事を参考にさせてもらうと以下の式が成り立ち、これらを連立方程式として解く、というものになります。

三角形上の任意の点Pの表し方1

P = v0 + edge1 * u + edge2 * v

三角形上の任意の点Pの表し方2

// レイを元に算出します
// origin ... レイの始点
// ray ... レイの方向
// t ... 交点までの距離
P = origin + ray * t

つなげて以下の方程式に変換

方程式

origin + ray * t = v0 + edge1 * u + edge2 * v

係数ありとなしに整理

(edge1 * u) + (edge2 * v) - (ray * t) = origin - v0

これを以下のように行列式に直します。

\begin{vmatrix}
a1 \\
a2 \\
a3
\end{vmatrix}
u + 

\begin{vmatrix}
b1 \\
b2 \\
b3
\end{vmatrix}
v + 

\begin{vmatrix}
c1 \\
c2 \\
c3
\end{vmatrix}
t =

\begin{vmatrix}
d1 \\
d2 \\
d3
\end{vmatrix}

こうした行列式は クラメルの公式 という方法で解くことができるようです。
（クラメルの公式については下の方で説明しています）

サンプルプログラム

今回のを元にサンプルプログラムを作ってみました。
下記サンプルは Three.js を利用したものとなっています。
なのでベクトルの扱いなどはThree.jsのものを利用しています。

/**
 *  三角形の内包判定
 *  
 *  @param vecA vectorA
 *  @param vecB vectorB
 *  @param vecC vectorC
 */
function det(vecA, vecB, vecC) {
    return ((vecA.x * vecB.y * vecC.z)
          + (vecA.y * vecB.z * vecC.x)
          + (vecA.z * vecB.x * vecC.y)
          - (vecA.x * vecB.z * vecC.y)
          - (vecA.y * vecB.x * vecC.z)
          - (vecA.z * vecB.y * vecC.x));
}

/**
 *  Raycast
 *
 *  @param origin origin vector of ray
 *  @param ray  ray direction
 *  @param v0 a vertex of a triangle
 *  @param v1 a vertex of a triangle
 *  @param v2 a vertex of a triangle
 *
 *  @return result object
 */
function rayIntersectsTriangle(origin, ray, v0, v1, v2) {
    // 交差判定結果を表すオブジェクト
    var  ret = {
        result: false,
        point: new THREE.Vector3(),
        distance: 0
    };
    
    // レイの逆方向のベクトルを得る
    var invRay = ray.clone().multiplyScalar(-1);
    var edge1 = (new THREE.Vector3()).subVectors(v1, v0);
    var edge2 = (new THREE.Vector3()).subVectors(v2, v0);
    
    // クラメルの公式の分母
    var denominator = det(edge1, edge2, invRay);
    
    // レイが平面と平行でないかチェック
    if (denominator <= 0) {
        return ret;
    }
    
    var d = (new THREE.Vector3()).subVectors(origin, v0);
    
    var u = det(d, edge2, invRay) / denominator;
    if ((u >= 0) && (u <= 1)) {
        var v = det(edge1, d, invRay) / denominator;
        if ((v >= 0) && (u + v <= 1)) {
            var t = det(edge1, edge2, d) / denominator;
            
            // 距離がマイナスの場合は交差していない
            if (t < 0) {
                return ret;
            }
            
            var tmp = ray.clone().multiplyScalar(t);
            ret.point = (new THREE.Vector3()).addVectors(origin, tmp);
            ret.result = true;
            ret.distance = t;
        }
    }
    
    return ret;
}

注意点

実際に実装してみて気づいたんですが、3Dの世界では三角形を描く頂点の順番が重要です。
逆周りに指定してしまうと普通は画面に表示されません。（いわゆるカリング）

このRaycastの実装も同様に頂点の扱いが重要で、逆順だと意味が変わってしまいます。
つまり「三角形の裏」からは、例え視覚的にはレイが交差していても、計算結果は交差していない結果となります。
（なので、サンプルのレイの方向を逆にすると裏からはヒット判定となりません）

動作サンプル

簡単な動作サンプルは jsdo.it にアップしてあります。

---

用語と各種解説

det（デターミナント）

行列を調べていると見かける det。意味は以下のようです。

Yahoo! 知恵袋より引用。

行列式のことです。

例えば2X2の行列A
(a,b)
(c,d)
に対して
det|A|=ad-bc
と定義されます。

例えば以下のような行列を例にすると、

\begin{vmatrix}
1 &2 \\
3 &4
\end{vmatrix}

=

(1 \times 4) - (2 \times 3) = -2

なお、2 x 2行列の場合はすぐに求めることができますが、3 x 3以上の行列になると色々とめんどくさいようです。
具体的な計算方法についてはこちらの記事が分かりやすかったです。

クラメルの公式（Cramer's rule）

ガブリエル・クラーメルさんが発表した公式。Wikipediaから引用すると以下の意味のようです。

未知数の数と方程式の本数が一致し、かつ一意的に解ける線型方程式系の解を明示的に書き表す行列式公式である。これは、方程式の解を正方係数行列とその各列ベクトルを一つずつ方程式の右辺のベクトルで置き換えて得られる行列の行列式で表すものになっている。

a_1 x_1 + b_1 x_2 = c_1 \\
a_2 x_1 + b_2 x_2 = c_2

という連立方程式があったとき（a, b, cは既知）、これを以下のような行列にして一意に解ける公式（であってるかな？）

\begin{vmatrix}
a_1 &b_1 \\
a_2 &b_2
\end{vmatrix}

\begin{vmatrix}
x_1 \\
x_2
\end{vmatrix}

=

\begin{vmatrix}
c_1 \\
c_2
\end{vmatrix}

この式の行列を $A$ と置き $Ax$ と書くとすると、
これを以下のようにして解ける。

x_i = \frac{det(A_i)}{det(A)}

ちなみにこの $i$ は任意の位置の $x$ であり、$det(A_i)$ は、該当箇所の列を、$c$ の列で置き換えたものとして扱う。
つまり、仮に $x_1$ を求めたい場合は、

det(A_1) = 
\begin{vmatrix}
c_1 &b_1 \\
c_2 &b_2
\end{vmatrix}

=

(c_1 \times b_2) - (b_1 \times c_2)

となります。