お久しぶりです！
数学やアルゴリズムの普及活動に取り組んでいる大槻 (通称： けんちょん) です。現在は、
- モノグサ株式会社のコンテンツアーキテクト (算数・数学や、プログラミングの教材設計や教材開発など)
- 株式会社NTTデータ数理システムの顧問 (AI に関する知見の提供や、各種講演活動など)
の仕事をしています。今回は「中学受験の算数」について書きます。中学受験の算数をテーマとした問題をたくさん出題します！
中学受験の算数には、昨今重要性が叫ばれているプログラミング的思考力を楽しく鍛えられるエッセンスが詰まっています。中学受験を志す児童や保護者の方々だけではなく、算数・数学の学び直しをしたい大人の方々や、AtCoder などのプログラミングコンテストに挑んでいるプログラマの方々にも有益な部分も多いと思います。
なお、この記事はモノグサアドベントカレンダーの 18 日目の記事として執筆しています (大変遅くなって申し訳ございません)。細かい話は抜きに、いきなり中学受験の算数の問題にチャレンジしたい方は「2 章： 簡単な文章題」からチャレンジしてみください！
目次
| 章 | タイトル | 内容 |
|---|---|---|
| 1 章 | はじめに | 本記事の趣旨をまとめます |
| 2 章 | 簡単な文章題 | まずは易しい問題を解いて肩慣らししましょう！ |
| 3 章 | 平面図形 | 図形から本質的情報を見抜く訓練をします！ |
| 4 章 | 特殊算 | 中受算数の定番！ つるかめ算などを解きます！ |
| 5 章 | 規則性 | 法則を発見する力を鍛えます！ |
| 6 章 | 最難関校の入試問題 | 最高峰の入試問題を解いてみましょう！ |
| 7 章 | 中学受験算数の攻略ポイント | 中受算数の偏差値別の攻略ポイントを解説します！ |
| 8 章 | 中学受験の光と影 | 中学受験そのものについて、さまざまな視点から議論します |
| 9 章 | 本記事の先へ | 本記事で扱えなかったテーマや、参考書籍を挙げます！ |
1 章： はじめに
中学受験とは、私立中学や国公立の中高一貫教育校などに入学するための試験を受けることです。中学受験に対しては、さまざまな立場の人がさまざまな感想を抱いていると思います。「中学受験とはこのようなものである」などと、一概に述べることは大変難しいでしょう。しかしながら、中学受験に関する難しい議論は本記事の最後の方に譲り、ここでは
中学受験の算数の問題には、プログラミング的思考を楽しく鍛えられるものが多い
ということを述べます。
1-1： 中学受験の算数と、プログラミング的思考力
最近の教育業界の大きな話題として、小学校や中学校におけるプログラミング教育の必修化が挙げられるでしょう。その目的は、プログラミング自体ができるようになることよりも、プログラミング的思考力を身につけることとされています1。
それでは、プログラミング的思考とはなんでしょうか。文部科学省は次のように定義しています (資料「小学校段階におけるプログラミング教育の在り方について（議論の取りまとめ）」より)。「組合せ」「組み合わせる」という言葉が何度も登場していますね。平たく言えば、解決したい問題に対して、必要な道具を組み合わせて、論理的に解決していく力のことですね。
ソニー・グローバルエデュケーションは、そのようなプログラミング的思考による問題解決のアプローチを、さらに次のように掘り下げています (資料「プログラミング的思考の中核を担う日本型算数・思考力教育」より)。問題を分解して考えて、法則を発見し、それを抽象化して、最後に解法を組み立てるということですね。
中学受験の算数では、まさに「分解する」「法則を発見する」「解法を設計する」といった力を要求する問題が数多く見られます。さらに、高度な問題になると、「抽象化する」という力も要求されるようになって来ます。大きな数についての問題を解くとき、最初に小さな数で実験して法則を発見し、その法則を一般的な数にも適用できるように抽象化して、結果的に大きな数に対しても解決できるようにする、といったアプローチは定番です。具体的な詳しいことは、2 章以降の問題で少しずつ述べていきます。
【関連】 ソニー・グローバルエデュケーションの「5 つの思考回路」
関連する話題として、ソニー・グローバルエデュケーションはさらに「論理的思考力」を次の 5 つの思考回路「スキャン」「クリエイト」「リバース」「ノック」「ステップ」に分解しています (参考資料： 思考力を鍛える方法)。これらの思考回路も、さまざまな問題を解決へと導く重要なものです。
| 思考回路 | 意味 | 詳細 |
|---|---|---|
| スキャン | 読みとる | 問題文や図から、必要な情報を読みとる |
| クリエイト | ひらめく | 問題を別の視点から見ることで、新たな解決方法をひらめく |
| リバース | 逆算する | 問題を解決するまでの道筋を、想像して逆算する |
| ノック | 洗い出す | ありうる可能性を、もれなく重複せずに洗い出す |
| ステップ | 組み立てる | 問題の解決に向けて、1 つひとつの順序を正しく組み立てる |
スキャン回路は、問題を正しく認識して、小問題へと分解するのに必要な力ですね。さらに、クリエイト回路・リバース回路・ノック回路を使うことで、法則を発見し、それを抽象化して「一般的に成り立つだろうと予想される仮説」を立てることができます。最後に、ステップ回路を使うことで、問題の解法を組み立てることができます。これらの思考回路は、まさにプログラミング的思考を支えるものだといえます。
さらに、プログラミングに限らず、仮説を立てて検証するという、あらゆる場面で重要な役割を果たす仮説検証の営みを支えるものでもあります2。なお、これらの論理的思考回路についてさらに具体的なことを経験したい方は、ソニー・グローバルエデュケーションによる書籍『５分で論理的思考力ドリル』を読むのがオススメです！
1-2： 中学数学や高校数学の「小学生版」であること
中学受験の算数というと、特殊なトレーニングだという印象を持つ人も多いかもしれません。しかし、実際には突拍子のないものではなく、
- 方程式や一次関数など、中学数学で学ぶ内容を、小学生の言葉で学ぶ
- 集合と命題や図形の性質など、高校数学で学ぶ内容を、小学生の言葉で学ぶ
といった内容が大半を占めています。中学数学や高校数学に熟練している人ならば、それらの一部を、小学生向けにデフォルメしたものであることが分かると思います。したがって、中学受験の算数を、何か特別なものだと思う必要はないでしょう。
一方、実際に中学受験の算数に触れている小学生たちにとっては、中学数学や高校数学に繋がる要素を吸収できることのメリットは大きいです。のちに中学数学や高校数学を学んだとき、「これはあの頃やったことを一般化したものだ！」と気づきを得る機会は多いと思います。このような、小学生時代に学んだことが抽象化されていく過程は、プログラミング的思考を大いに育む営みだといえます。
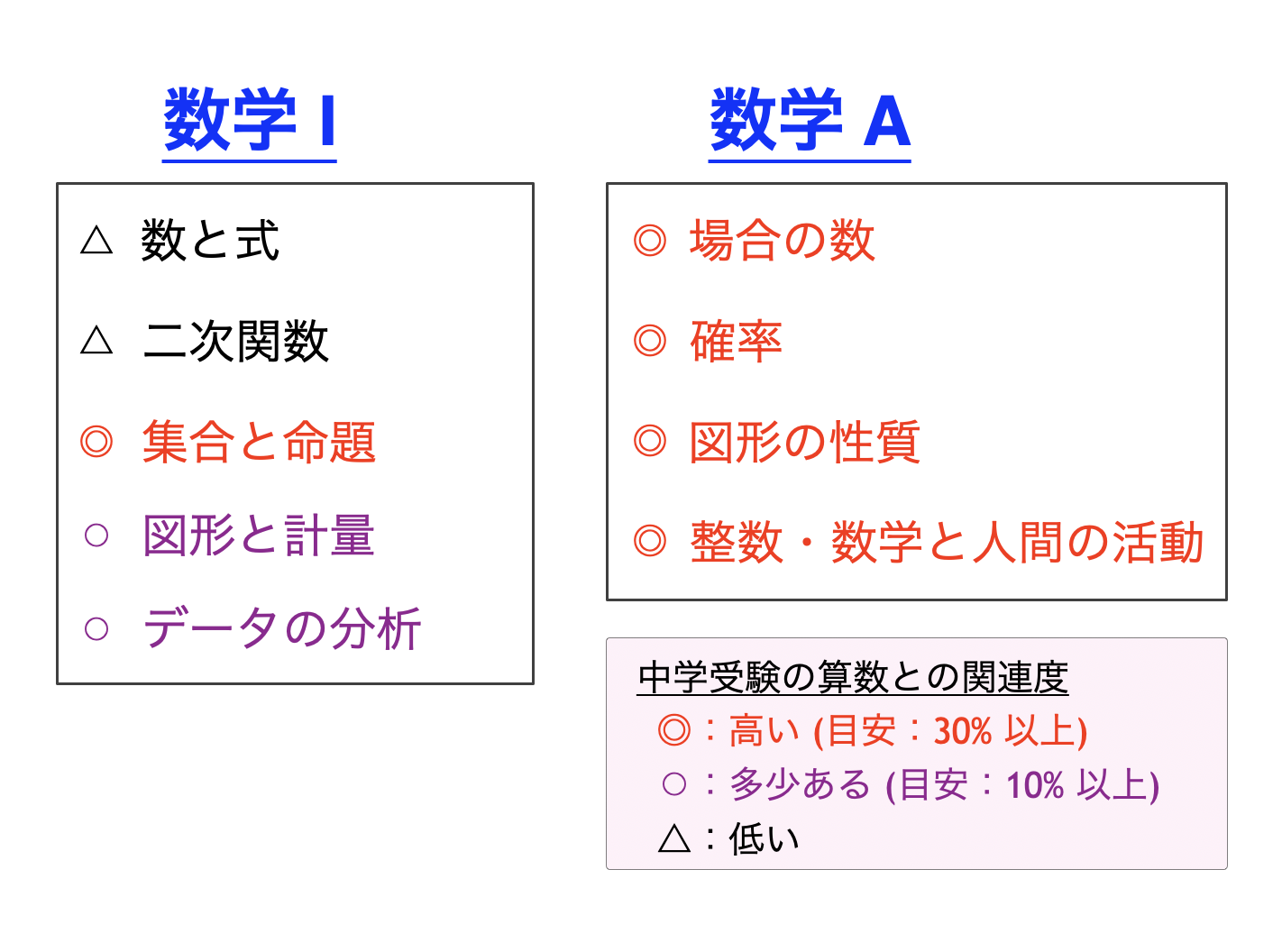
特に、数学 IA は、中学受験との親和性がとても高いです。数学 IA の最初の方で学ぶ単元「数と式」「二次関数」に関しては、中学受験に登場しない部分が多いですが、それ以外の単元は中学受験の算数との関連が深いです。単元「場合の数」「確率」「整数・数学と人間の活動」はもちろんのこと、「集合と命題」「図形と計量」「図形の性質」なども、中学受験を経験しているとスッと入って来る要素を多く含んでいます。
それらのことについても、この後の問題集の中で紹介できればと思います。
1-3： 本記事のねらい
本記事の目的は、プログラミング的思考を育んでくれるような、中学受験の算数の世界を紹介することです。中学受験に少しでも興味のある人全員に向けて書いています:
- 実際に中学受験をしたいと考えている小学生の方
- 中学受験について情報を得たい保護者の方
- 中学受験未経験であるため、それがどんなものかを知りたい大人の方
- 算数や数学が苦手だったが、エンジニアリングや事務処理の仕事をしていくうちに、数学的思考力の重要性に気がついて、その学び直しをしたい大人の方
- 中学受験そのものには興味はないが、論理的思考力に自信があって、腕試しをしたい方
- とにかく算数や数学が好きで、問題を解くことを楽しみたい方
- AtCoder などのプログラミングコンテストに挑むのに必要となる算数や数学のセンスを磨きたいエンジニアの方
誰が読んでも楽しめるように心がけました。各対象別に読んでほしいポイントを挙げます。
中学受験をしたい小学生の方へ
難しいことは考えずに、とにかく問題を解いてみてください。どこまで解けるか、自分の腕を試してみましょう！
中学受験について情報を得たい保護者の方へ
算数の教え方について自信が持てない保護者の方も多いと思います。そこで、本記事では、子どもが躓きやすいポイントについても紹介するように心がけました。ぜひ参考にしてみてください！
数学的思考力の重要性に気づいて学び直したい大人の方へ
数学の学び直しにおいては、中学数学を押さえたあとは、ぜひとも数学 IA まで到達したいところだと思います。しかしながら、中学数学から数学 IA へのステップアップは容易ではありません。
そんなときは、一旦肩の力を抜いて、中学受験の算数のようなパズルに触れてみるのも有効だと思います。本記事では、数学 IA の習得にも繋がるポイントも数多く解説しています。ぜひこれらのポイントを習得して、数学 IA にも挑戦してみてください！
AtCoder で好成績をおさめたい競技プログラマの方へ
AtCoder の提唱する「世界を目指すための練習法」では、高校数学の基礎知識と、 中学受験レベルの算数能力は、AtCoder に挑む上での前提知識であるとしています3。実際に、AtCoder で出題される問題を解決する思考力を鍛えるためには、中学受験の算数に触れることはあらゆるレベルで有益だと思います。
さらに、個人的にオススメの練習方法は、中学受験の算数の問題に対して、具体的な数値を一般化した問題を解くことです。中学受験の算数の問題を一般化したような問題は、実際に AtCoder でも出題されています。
1-4： 本記事の例題の難易度
本記事では、中学受験の算数をテーマとした問題を、易しいものから難しいものまで紹介します。具体的には、大手学習塾である四谷大塚の合格確率 80% 判定の偏差値で 30 レベルの問題から 70 以上のレベルの問題まで紹介します4 。
各問題の難易度を便宜上 5 段階で表記しています。これらは次のような目安になっています。しかし、これらはあくまで目安であって、厳密なものではありませんので気楽に捉えていただけたらと思います5。
| 難易度 | 四谷大塚の偏差値の目安 |
|---|---|
| ★☆☆☆☆ | 30〜40 |
| ★★☆☆☆ | 40〜50 |
| ★★★☆☆ | 50〜60 |
| ★★★★☆ | 60〜70 |
| ★★★★★ | 70〜 |
2 章： 簡単な文章題 〜 まずは肩慣らし！ 〜
まずは簡単な文章題から解いてみましょう！ この章の文章題は、のちの章に繋がるものも多く集めています。
例題 1： 将棋盤 (難易度 ★☆☆☆☆)
【問題文】
将棋盤は $9 \times 9$ のマス目からなっています。合計で何マスあるでしょうか。
答え
解説
まずは、足し算・引き算・かけ算・割り算の感覚をしっかり養うことが重要です！
【さらなる話題】
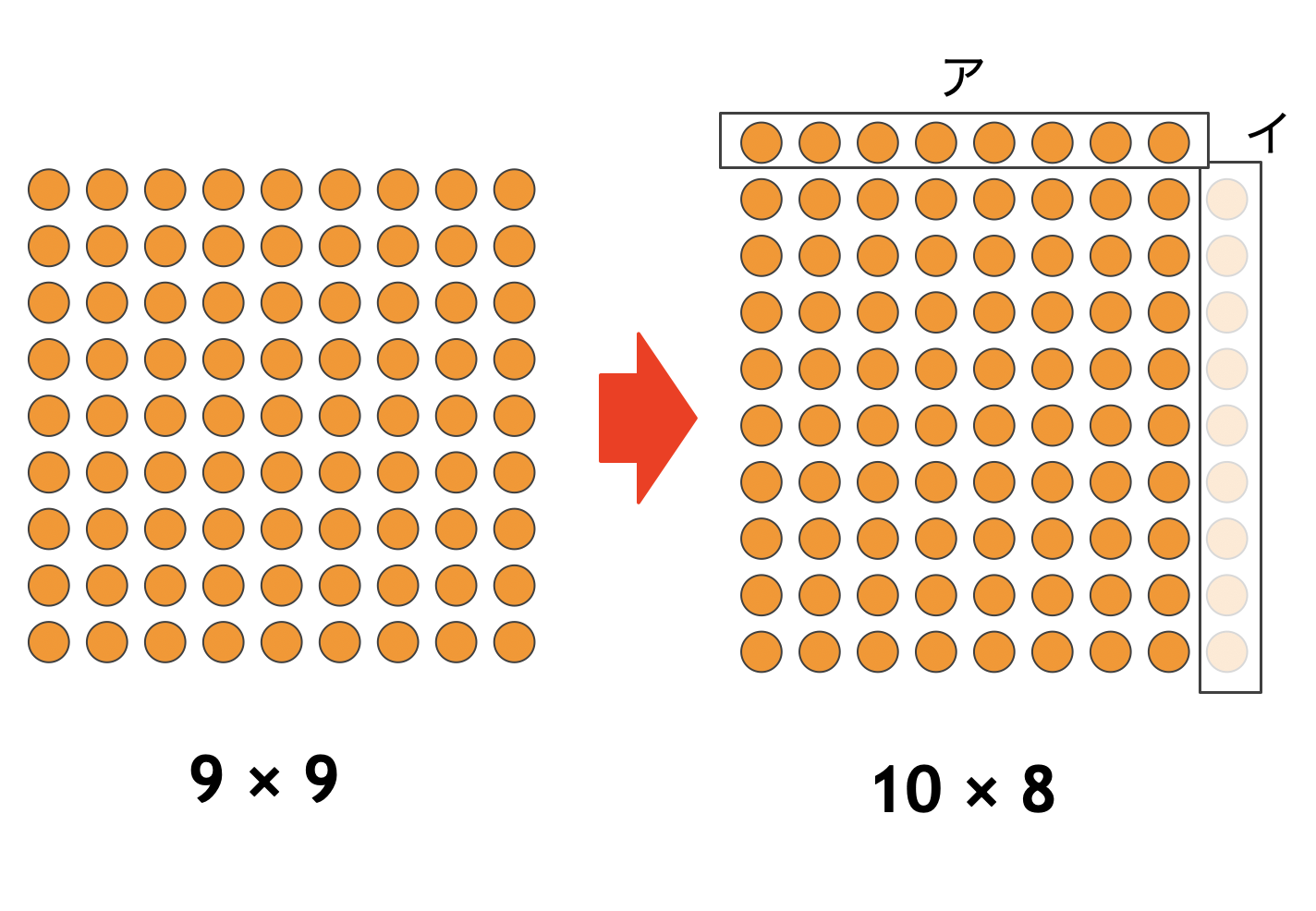
将棋盤の縦のマス数を $1$ 増やして、横のマス数を $1$ 減らすと、マス目の個数は
$10 \times 8 = 80$
となって、もとの将棋盤よりも $1$ だけ減ります。これが偶然なのか、必然なのか、ぜひ考えてみてください！
- 大人向けのヒント： $(x + a)(x - a) = x^2 - a^2$ という、中3で学ぶ乗法公式が使えます。
- 子供向けのヒント： 下図を参考にしてみてください。アの部分には $8$ 個、イの部分には $9$ 個ありますね。
なお、こうした話題も、中学受験の算数で好んで出題されます。たとえば、
- 将棋盤のような小さな盤で計算させる
- $1000 \times 1000$ のような大きな盤でも、「縦を $1$ 増やし、横を $1$ 減らすと、マス数が $1$ 減る」という法則が成り立つのかを推測させる
というような流れが考えられます。この思考の流れはまさに、ソニー・グローバルソリューションズの提唱する「法則を発見する」「抽象化する」というプログラミング的思考ですね。
特に、最近の中学入試では、会話文の中の空欄を埋めてもらう形式の問題が増えています。「縦を $1$ 増やし、横を $1$ 減らすと......」などのような設定は、会話文形式の問題の題材にうってつけですね。たとえば、2023 年に晃華学園中学校 (第 1 回) の第 6 問で出題されています6。
例題 2： バスが何台必要か (難易度 ★☆☆☆☆)
続いて、次の問題を解いてみましょう。
【問題文】
$108$ 人の子どもたちがバスに乗って修学旅行に行きます。$1$ 台のバスには $20$ 人の子どもが乗ることができます。バスは少なくとも何台必要でしょうか。
答え
解説
$108 \div 20 = 5$ あまり $8$
より、$5$ 台のバスに満員まで乗せた上で、$8$ 人余ることがわかります。この $8$ 人の乗るバスがあと $1$ 台必要ですから、必要なバスの台数は
$5 + 1 = 6$ 台
例題 1 のかけ算に続いて、例題 2 は割り算です！
【さらなる話題】
問題を抽象化する
主にプログラマ向けの追加の話題です。この例題が簡単に感じた方は、ぜひ問題を抽象化して、
- 子どもの人数：$N$ 人
- $1$ 台あたりの定員：$X$ 人
($N, X$ はともに正の整数とします)
とした場合のバスの必要台数を求める方法を考えてみてください。そして、それをプログラムとして実装してみましょう！
抽象化した問題の解法
$N$ を $X$ で割ったときの商を $q$、余りを $r$ としましょう。
- $r = 0$ のとき (割り切れるとき)：バスの必要台数は $q$ 台です
- $r \neq 0$ のとき (割り切れないとき)：バスの必要台数は $q + 1$ 台です
さらに、実は、ワンライナーで解くこともできます。答えは「$N + X - 1$ を $X$ で割った商」に一致します。そのようになる理由もぜひ考えてみてください7。
例題 3： 植木算 (難易度 ★☆☆☆☆)
いよいよ、中学受験の算数の定番「植木算」です。
【問題文】
あるマラソンコースでは、スタート地点とゴール地点を含めて、$400$ m おきに $8$ 箇所の給水所があります。このマラソンコースのスタート地点とゴール地点は何 m 離れているでしょうか。
また、$2$ 箇所目の給水所と $6$ 箇所目の給水所の間は何 m 離れているでしょうか。
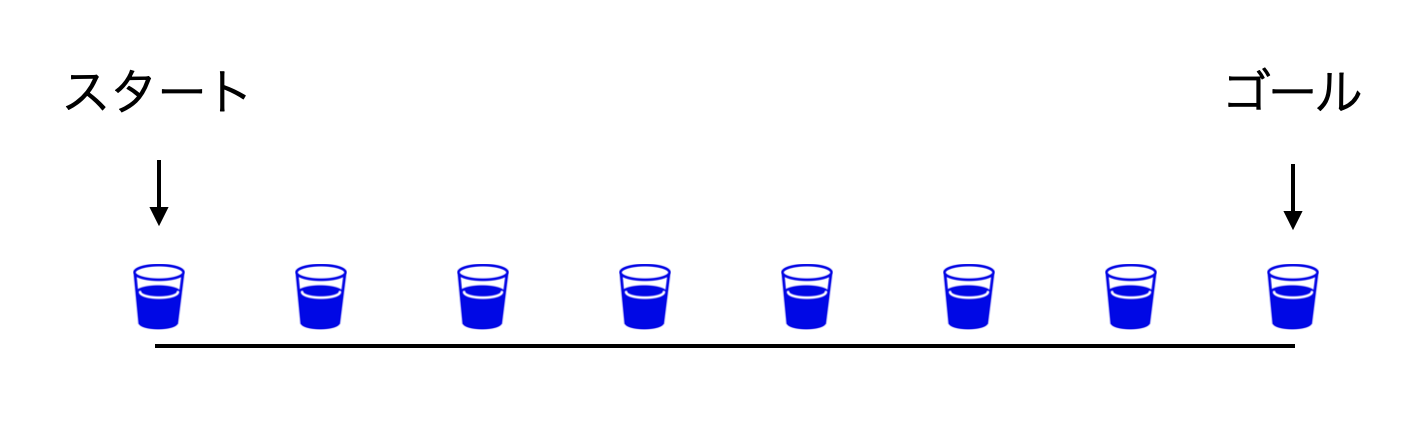
答え
スタートとゴールの間隔：$2800$ m
$2$ 箇所目と $6$ 箇所目の給水所の間隔：$1600$ m
解説
給水所が $8$ 個あるとき、「給水所と給水所の間」は $8 - 1 = 7$ 箇所あります (これが植木算の考え方です)。よって、スタート地点とゴール地点の間隔は
$400 \times 7 = 2800$ m
次に、給水所に $1, 2, 3, 4, 5, 6, 7, 8$ と番号を振ってみましょう。下図のようになります。
$2$ 個目の給水所と $6$ 個目の給水所の間には、「間」が $6 - 2 = 4$ 箇所あることが見て取れます。よって、その長さは
$400 \times (6 - 2) = 1600$ m
と求められます。
植木算は物に番号を振ると分かりやすいと思います。たとえば、下図のように $8$ 個の物があるとき、$1, 2, 3, 4, 5, 6, 7, 8$ と番号を振りましょう。
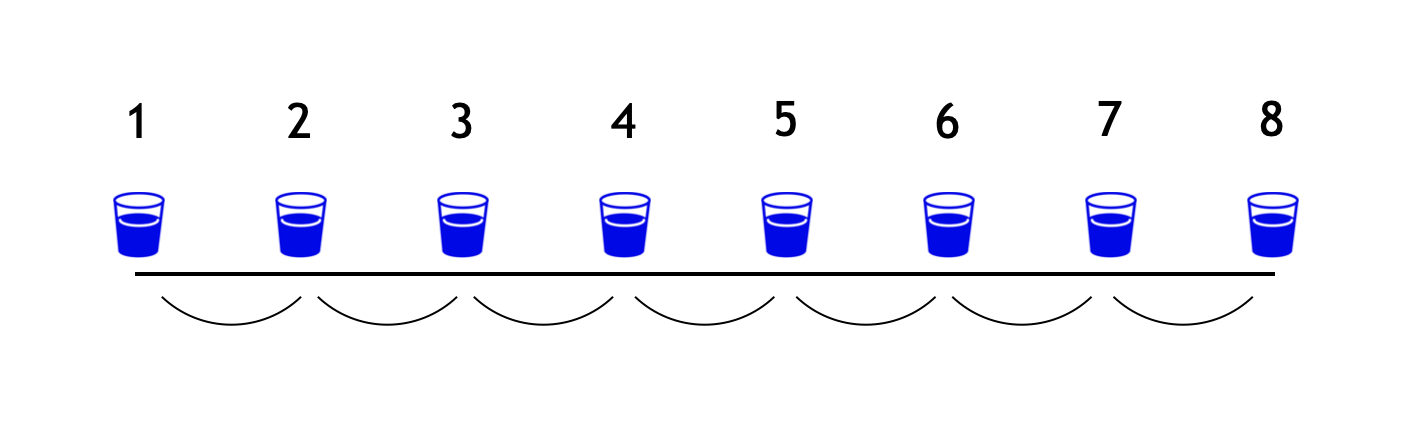
このとき、スタートは $1$ 番目、ゴールは $8$ 番目なので、その間は
$8 - 1 = 7$ ヶ所
と求められます。植木算の「$-1$」は、スタートの $1$ なのです8。
中学受験では、植木算を機械的に攻略されることを防ぐために、次のような問題もよく出題されます。
池の周りに $8$ 本の木を植えたところ、木の間隔はどこも $5$ m でした。池のまわりの長さは何 m ですか。
このような「スタートとゴールが繋がるようにグルッと回る」場合は、「木の数」と「間の数」は等しいです。「スタートとゴールの間」が増えるためです。よって、池のまわりの長さは
$5 \times 8 = 40$ m
です。
【さらなる話題】
等差数列の □ 番目
$2, 6, 10, 14, \dots$
のように、隣り合う数の差 (交差といいます) が一定である数列を等差数列といいます。等差数列の $□$ 番目の数は次の式で求められます。
等差数列の $□$ 番目の数 $=$ はじめの数 $+$ 交差 $\times$ $(□ - 1)$
数列の「はじめの数」から「$□$ 番目の数」まで順に $1, 2, \dots, □$ と番号を振ってみましょう。このとき、「はじめの数」から「$□$ 番目の数」まで、間隔が $□ - 1$ 個あります (これはまさに植木算の考え方です)。
よって、「はじめの数」に「交差」を $(□ - 1)$ 回足すことで、「$□$ 番目の数」が求められるのです。
例題 4： 周期算 (難易度 ★★☆☆☆)
植木算の考え方が身についていれば、周期算もこなせます！ 曜日に関する問題を解いてみましょう。
【問題文】
$2023$ 年 $12$ 月 $24$ 日は、日曜日です。
$2024$ 年 $12$ 月 $24$ 日は、何曜日でしょうか。
($2024$ 年はうるう年であることに注意しましょう)
答え
解説
$2024$ 年はうるう年ですので、$2024$ 年 $12$ 月 $24$ 日は、$2023$ 年 $12$ 月 $24$ 日の $366$ 日後です。ここで、$366$ を $7$ で割ると
$366 \div 7 = 52$ あまり $2$
です。つまり、$366$ 日経過する際に、$52$ 週間と $2$ 日が経過するということです。日が経過する前の $2023$ 年 $12$ 月 $24$ 日は日曜日であり、
- その $52$ 週間経過後は、日曜日である
- さらに $2$ 日経つと、火曜日になる
よって、$2024$ 年 $12$ 月 $24$ 日は火曜日です。
曜日算では、経過日数を考えることが最初のポイントとなります。
また、$1$ 年後の同じ日は、うるう年以外では曜日が $1$ 個だけ進むということは、覚えておいて損はないでしょう。
【さらなる話題】
曜日は $7$ 日ごとに同じことを繰り返します。このように同じことを繰り返す性質を周期性と呼びます。
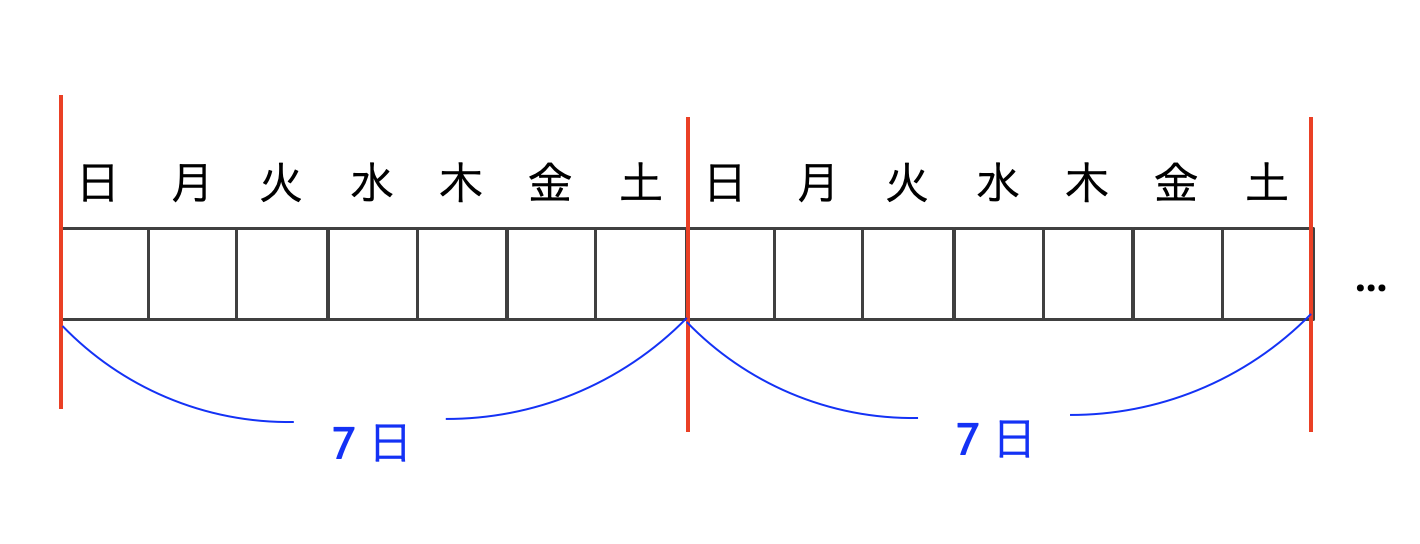
中学入試の算数では、周期性を的確に見抜くことが大切になる問題が数多く出題されています。「5 章： 規則性」では、そのような問題もいくつか紹介します。
例題 5： 等差数列の和 (難易度 ★★☆☆☆)
続いて、実用的な問題を解きます。
【問題文】
$10 + 14 + 18 + 22 + \dots + 90$
を計算するといくつになるでしょうか。なお、これは $10$ から $90$ までの数を、$4$ 飛ばしで足したものです。
答え
$1050$
解説
まず、$10$ から $90$ まで、$4$ 飛ばしで何個の数があるかを考えましょう。全部書き出してもよいのですが、計算で求めることもできます。
$10 + 14 + 18 + 22 + \dots + 90$ を仮に全部書き出したとすると、記号「＋」は全部で
$(90 - 10) \div 4 = 20$ 個
あります。よって、足している数の個数は、
$20 + 1 = 21$ 個
です (植木算の逆をやっています)。
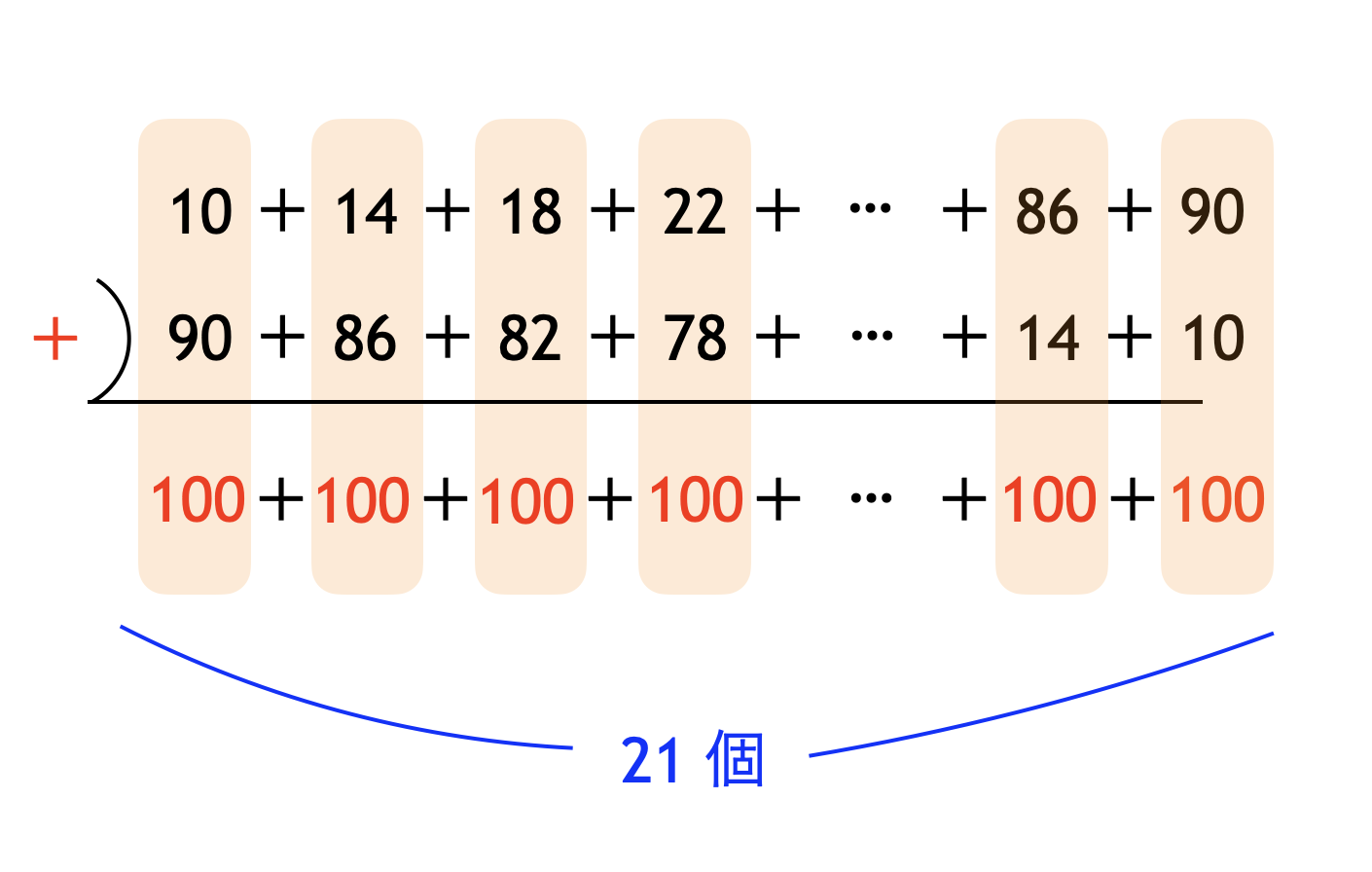
いよいよ、等差数列の和を考えます。等差数列の和を求めるためには、「足し算を逆にしたものを並べて縦に足す」という定番手法が使えます。この手法を使うと、下図のように $100$ という同じ数が $21$ 個登場します。求めたい和はこの半分ですので、
$100 \times 21 \div 2 = 1050$
と計算できます。
今回の解説の方法を使うことで、一般に次のことがいえます。
等差数列の和 $=$ (はじめの数 + 終わりの数) $×$ 個数 $\div$ $2$
等差数列の和は、
- はじめの数
- 終わりの数
- 個数
という $3$ つの値をすべて揃えるように意識すると、求めやすいです。今回の問題では「はじめの数」と「終わりの数」が最初からわかっていて「個数」の情報が不足していました。
一方、「はじめの数」と「個数」が最初からわかっていて「終わりの数」の情報が不足するケースも多いです。ぜひ、そのような設定の問題も自らの手で作って解いてみてください！ 問題を自作してみることも、とても有効な勉強になります。
【さらなる話題】
$m$ で割って $r$ 余る数
中学受験の算数では、$m$ で割って $r$ 余る数を上手に扱うことを要求する問題が多く出題されます。一例として、次の抽象化された問題を考えてみてください9！
【問題】
$m$ で割って $r$ 余る整数のうち、$k$ 以下である最大の整数を求めてください。
($m, r, k$ を $0$ 以上の整数とし、$r < m$ かつ $r \le k$ とします)
問題の解答
結論から言えば、「$k - r$ 以下である最大の $m$ の倍数」を求めて、それに $r$ を足せばよいです。
そのように考えて良い理由を考えてみましょう。たとえば、「$4$ で割って $2$ 余る整数のうち、$100$ 以下である最大の整数」を求めたいとします。$4$ で割って $2$ 余る数は考えづらいので、下図のように、それらをすべて一律に $2$ 引くことにします。このとき、目標値である $100$ からも $2$ を引けば帳尻が合います。
つまり、「$4$ の倍数のうち、$98$ 以下である最大の整数」を求めればよいことになります。世界のすべての数から $2$ を減らした数の世界で物事を考えるのです。
$98 \div 4 = 24$ あまり $2$
より、$98$ 以下の最大の $4$ の倍数は $24 \times 4 = 96$ です。最後に、一律に引いた $2$ を足して、
$96 + 2 = 98$
と求められます。
ここで、もとの問題に戻ります。$k - r$ を $m$ で割ったときの商を $q$ とすると、$k - r$ 以下の最大の $m$ の倍数は $qm$ です。よって、求める「$m$ で割って $r$ 余る整数のうち、$k$ 以下である最大の整数」は
$qm + r$
と求められます。
3 章： 図形問題 〜 本質的情報を見抜く！ 〜
図形問題も、中学入試で好んで出題されます。図形問題のポイントとして「補助線を思いつくか」を挙げる人は多いと思います。しかし、本当に天才的な補助線のひらめきが必要とされるのは、偏差値 70 以上の最難関校における話だと思ってよいでしょう。ほとんどの図形問題は、パターン化できます。問題から必要な情報を素早く見抜く力を磨きましょう10！
例題 6： 簡単な角度の問題 (難易度 ★☆☆☆☆)
まずは、簡単な角度の問題を解いてみましょう。
【問題文】
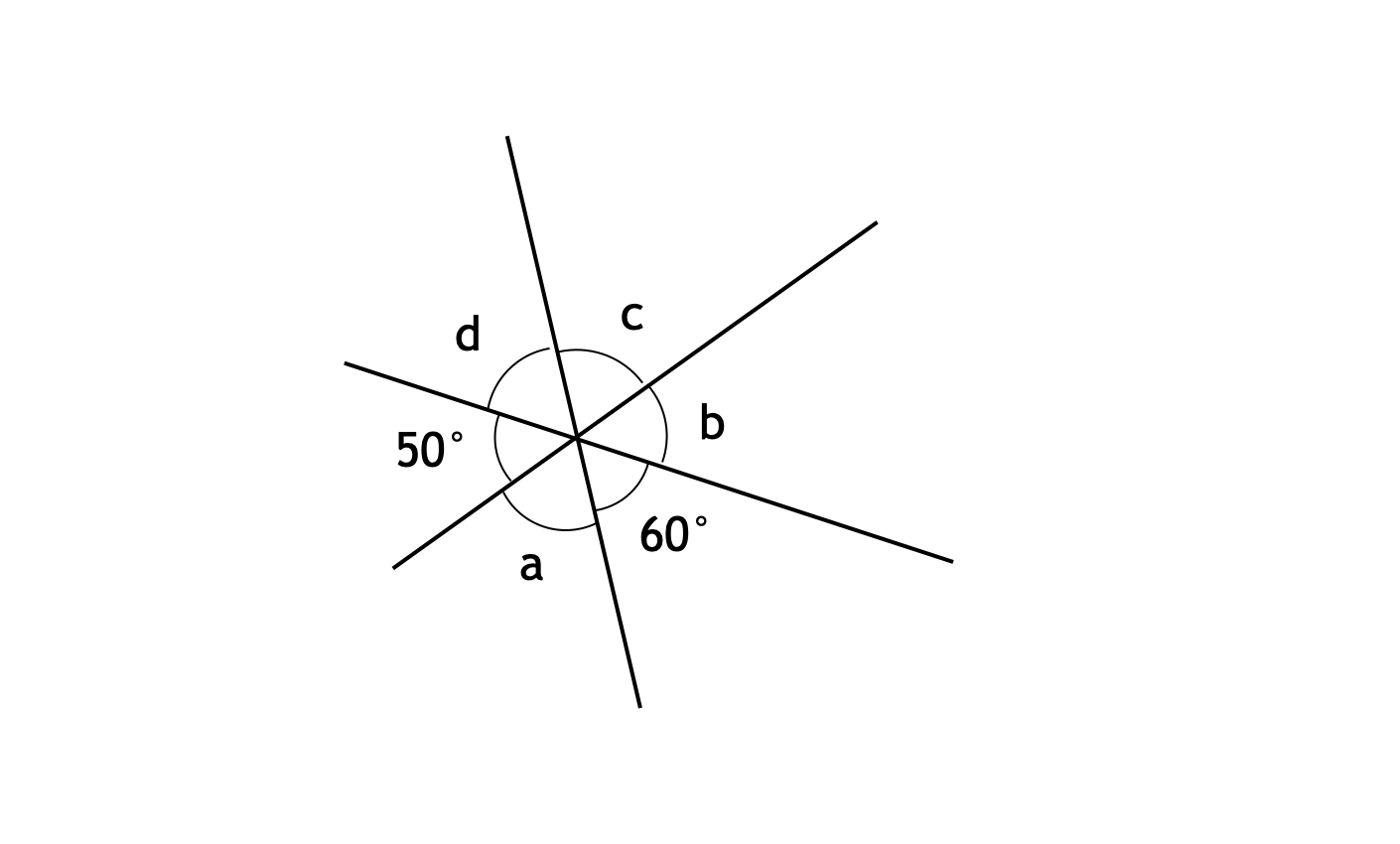
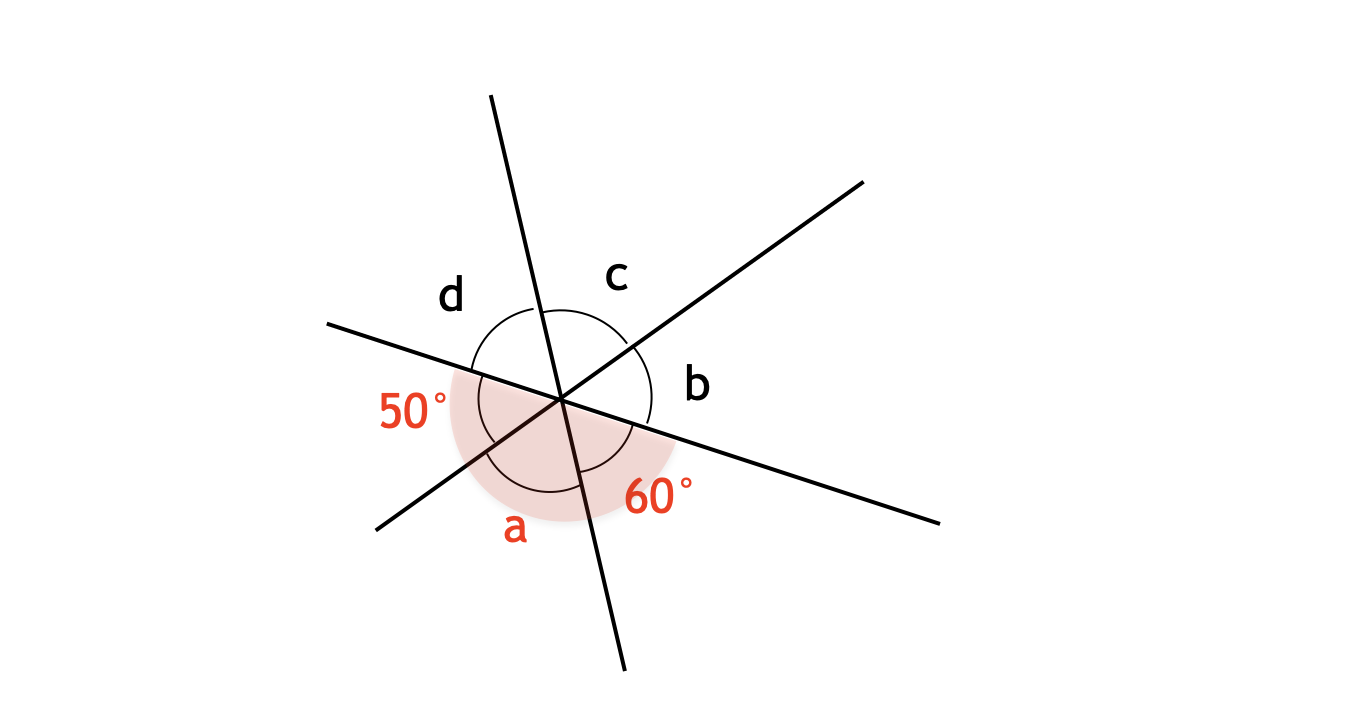
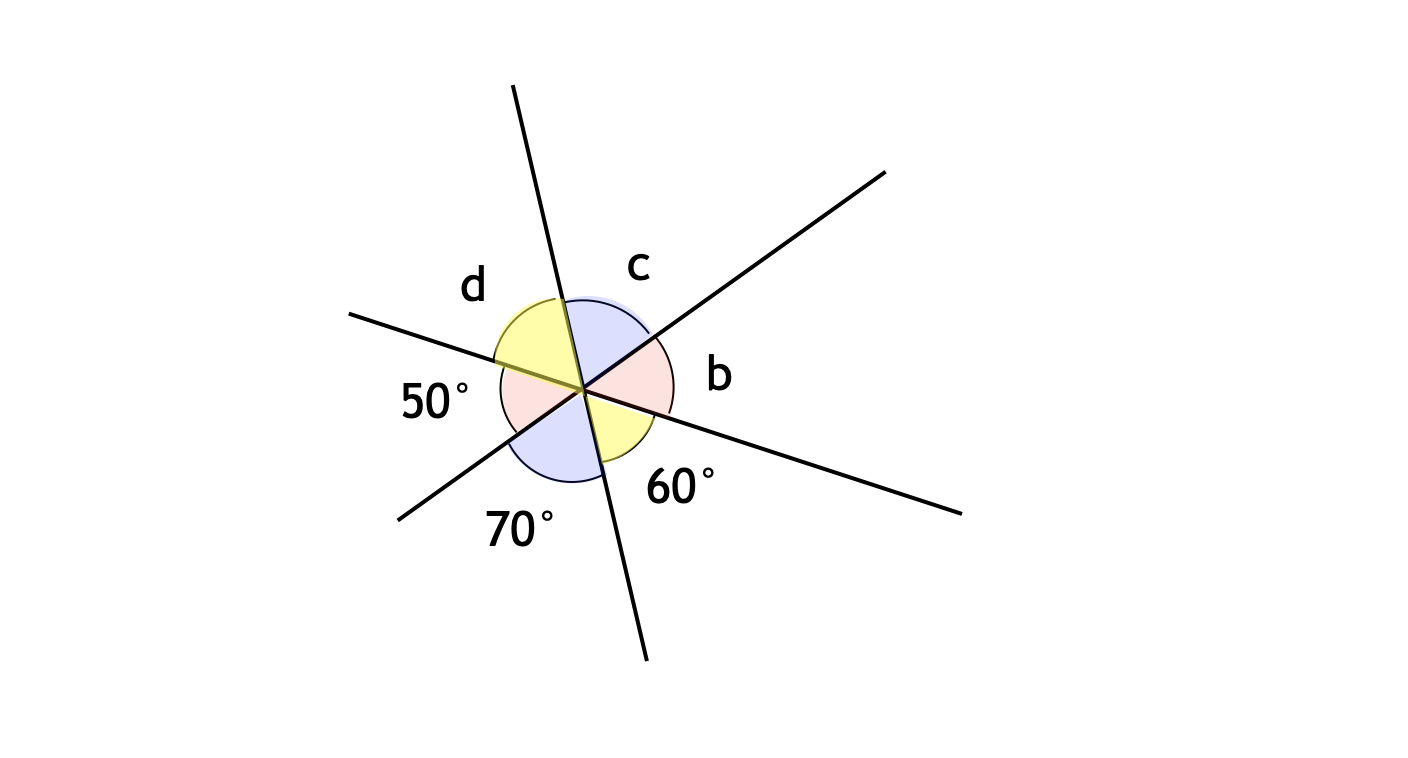
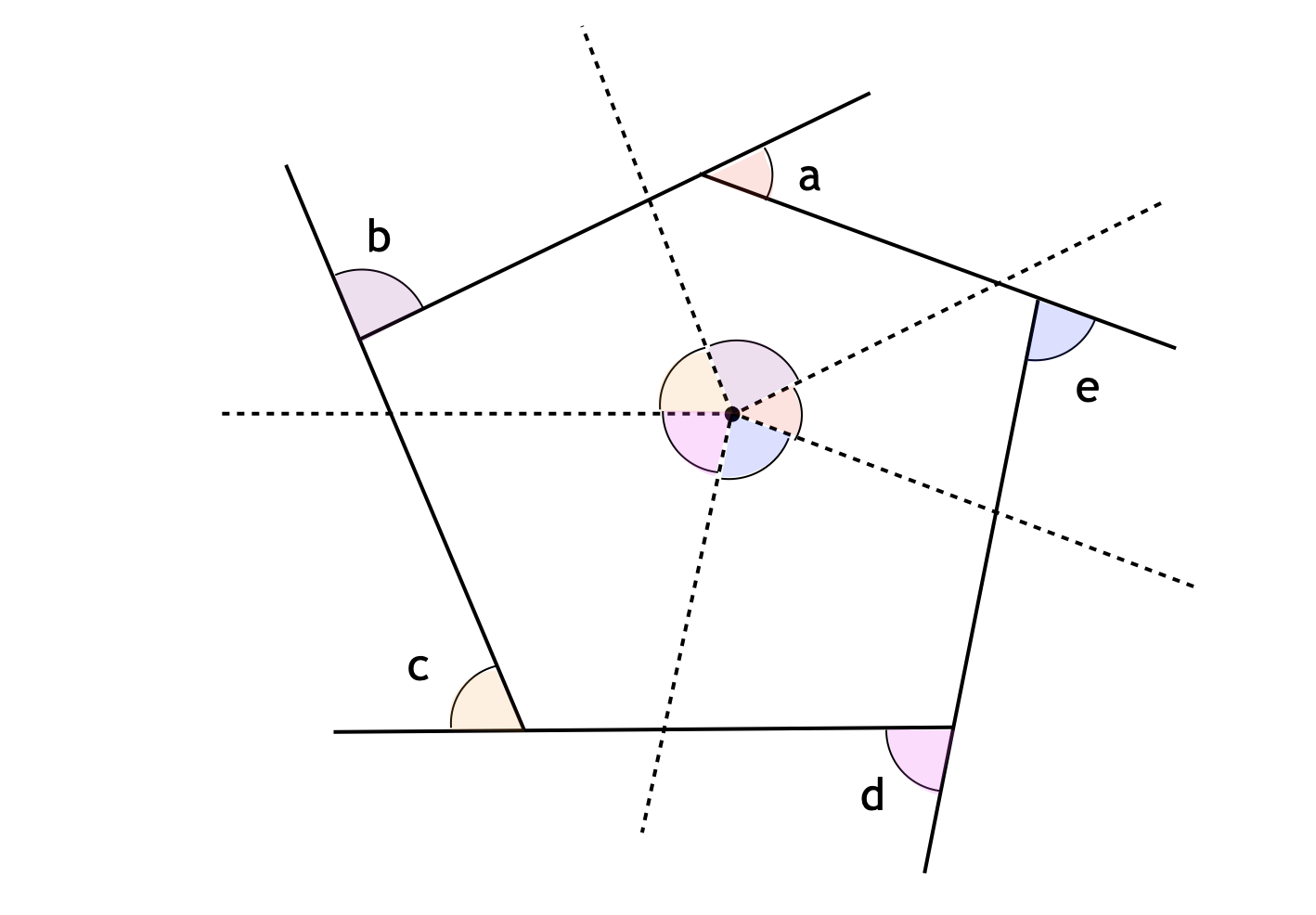
次の図において、∠$a$、∠$b$、∠$c$、∠$d$ は何度でしょうか。
【解説】
答え
解説
∠$a = 180 - 50 - 60 = 70$°
続いて、「対頂角が等しい」ことを利用して、残りの角を求めましょう。下図の、同じ色がついた角度は等しいです。よって、
∠$b = 50$°、∠$c = 70$°、∠$d = 60$°
と求められます。
図形問題では、「たいていの角度や長さは原理的には計算できるものなのだ」と思えることが大切です。また、図形問題に強くなるためには、問題で問われていない部分も含めて、全部の角度や長さを求めてみるのも有効なトレーニングです。ぜひやってみましょう！
【さらなる話題】
「自由度」の考え方
図形問題で意識したい概念として、自由度があります。自由度とは、その図形の形を決めるのに何個の情報が必要かを表す値です。自由度は、機構学やロボット工学では中心的な役割を果たす概念でもあります。
今回の図形は「$3$ 本の直線が $1$ 点で交わっている」という構図です。この構図において、すべての角度を決定するのに必要な情報量は $2$ 個です。つまり、自由度は $2$ です。
自由度に関する有名な話題としては、中2で学ぶ三角形の合同条件があります。三角形の合同条件としてよく知られているのは、次の $3$ つです。
- $3$ 本の辺の長さ ($3$ 辺相等などともいいます)
- $2$ 本の辺の長さと、その間の角の大きさ ($2$ 辺きょう角相等などともいいます)
- $2$ 個の角の大きさと、その間の辺の長さ ($2$ 角きょう辺相等などともいいます)
いずれも、$3$ 個の情報によって、三角形の形がただ 1 つに決まることを主張しています。つまり、三角形の形状の自由度は $3$ であるといえます。
さらに発展的な話題ですが、数学IAを履修済みの方は、具体的に三角形の $3$ 個の情報から、残りの辺の長さや角の大きさなどを求める方法も考えると楽しいと思います。$\sin, \cos, \tan$ や、余弦定理などが活躍します。
例題 7： 平行線の問題 (難易度 ★★☆☆☆)
続いて、平行線に関する有名な問題を解きます。
【問題文】
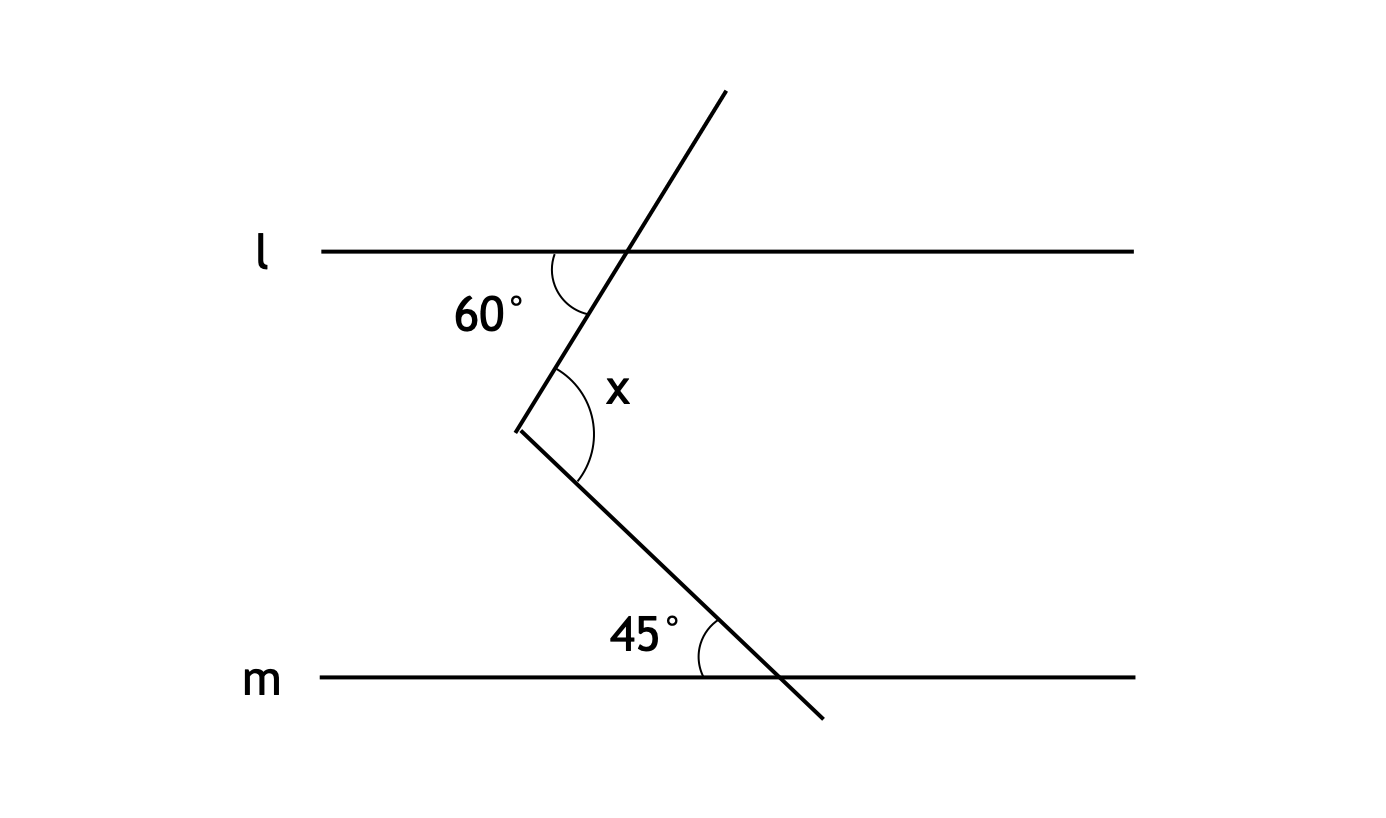
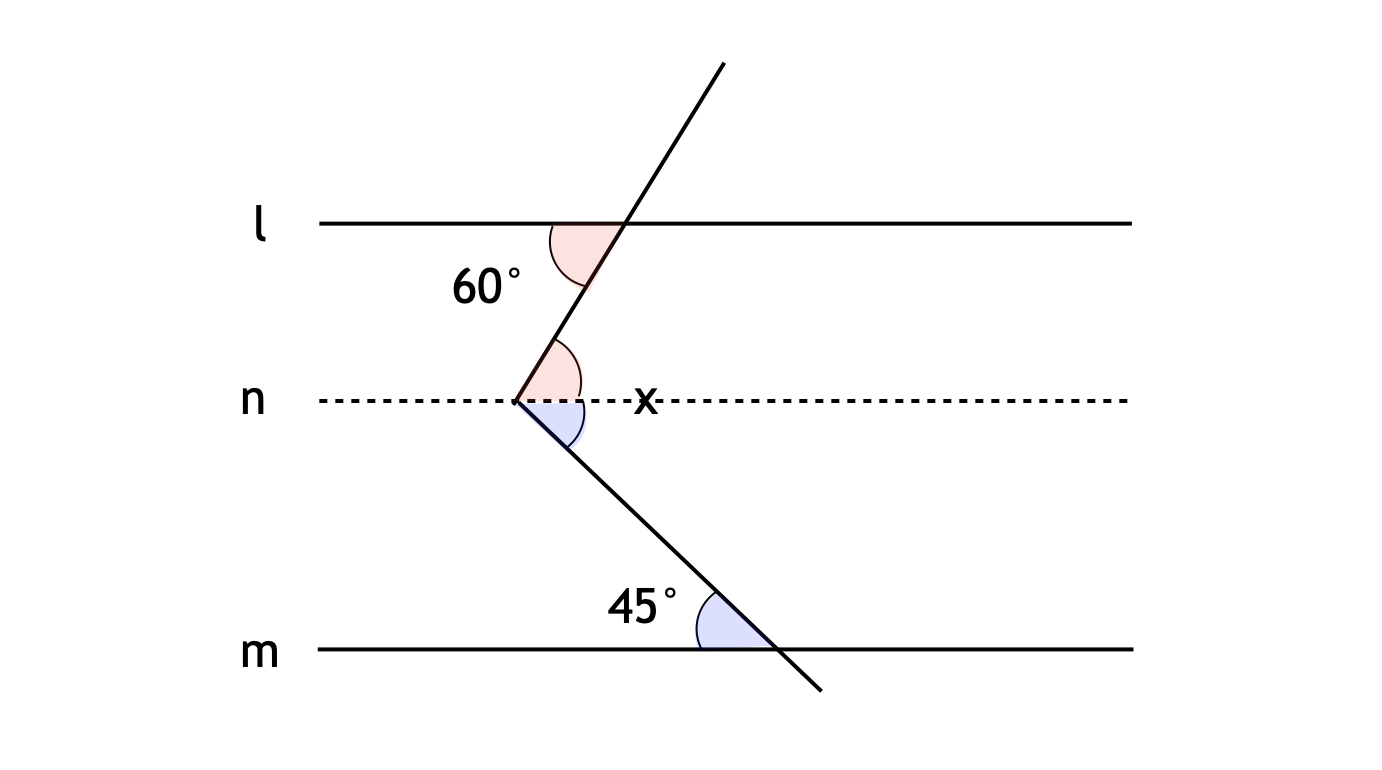
次の図において、直線 $l, m$ は平行です。このとき、∠$x$ は何度でしょうか。
答え
解説
平行線の錯角が等しいことを活用します。錯角とは、$2$ 本の直線に $1$ 本の直線が交差しているときの、斜め向かいに位置する角のことです。下図の赤い角度の組は「平行線の錯角」であり、等しいです。
平行線に関する問題では、折れ曲がっている点などの特徴的な点に対して平行線を引くことで活路が見出せることが多くあります。下図のように平行線 $n$ を引いてみましょう。このとき、赤い角同士の大きさと青い角同士の大きさがそれぞれ等しくなります。よって、求める ∠$x$ は、
∠$x = 60 + 45 = 105$°
平行線の問題では、錯角が等しいことを活用することで、活路が開けることが多いです。下図のように、 Z 型や逆 Z 型を探すように意識すると考えやすくなるでしょう。
一般に、図形に関する技術を習得するためには、自分なりのイメージを膨らませていくことが有効です。たとえば、人によっては、教習所のシビアな右折や左折を想像することで、等しい錯角を見つけやすくなるかもしれません。
【さらなる話題】
多角形の外角の和が $360$°
平行線の性質を上手に活用すると、多角形の外角の和が $360$° であることも説明できます。たとえば下図の多角形の外角の和を求めてみましょう。∠$a, b, c, d, e$ の総和を求めます。
下図のように、$1$ 点 $P$ をとって、各辺と平行な線を引いていきます。そうすると、同じ色の角度は等しくなります。よって、
∠$a +$ ∠$b +$ ∠$c +$ ∠$d +$ ∠$e = 360$°
となります。
例題 8： チーズケーキ (難易度 ★★☆☆☆)
次は、中堅校で頻出の面積の問題を取り上げます。円形のチーズケーキを $12$ 等分したときに登場する形です。
【問題文】
次の図の三角形の面積は何 cm² でしょうか。
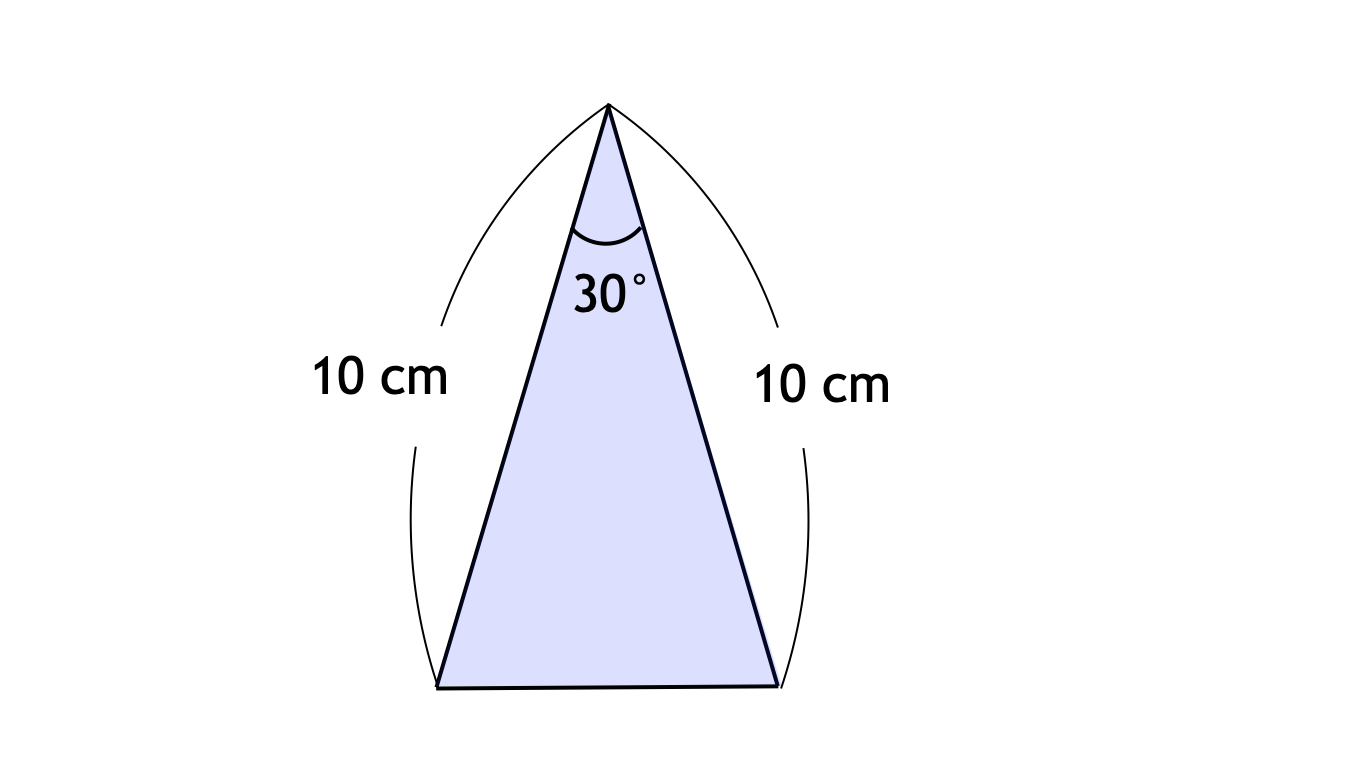
答え
$25$ cm²
解説
下図のように、$30$° ではない角の頂点から対辺へと垂直な線を引いてみましょう (下図の赤点線)。斜めに垂線を引くというのは、少し発想が難しいかもしれないですね。このとき、この垂線の長さは $5$ cm となります。
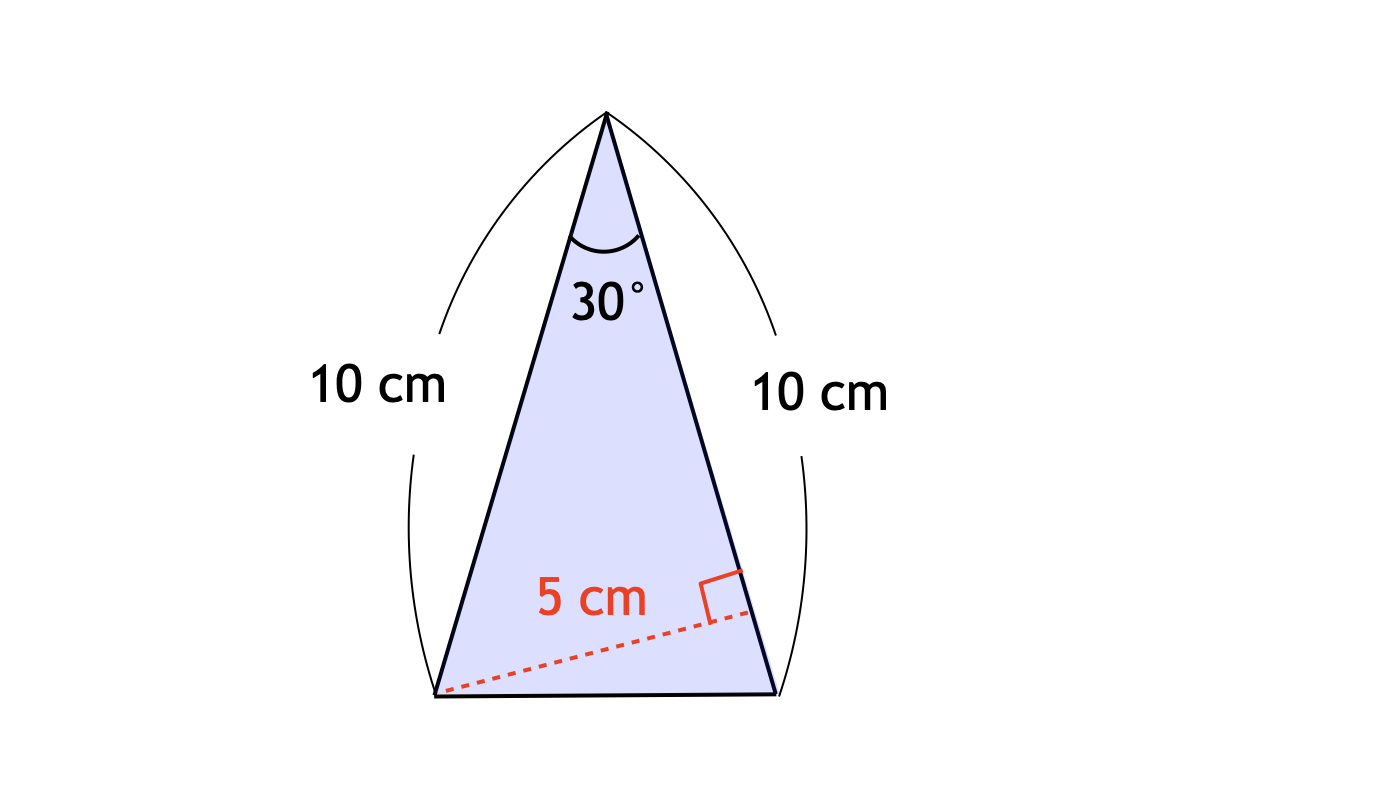
その理由は、下図の左側に示すように、内角が $30$°、$60$°、$90$° であるような直角三角形の辺の比は $2 : 1$ になっているからです。そしてその事実は、下図の右側に示すように、内角が $30$°、$60$°、$90$° である直角三角形が「正三角形の半分」であることから示せます。
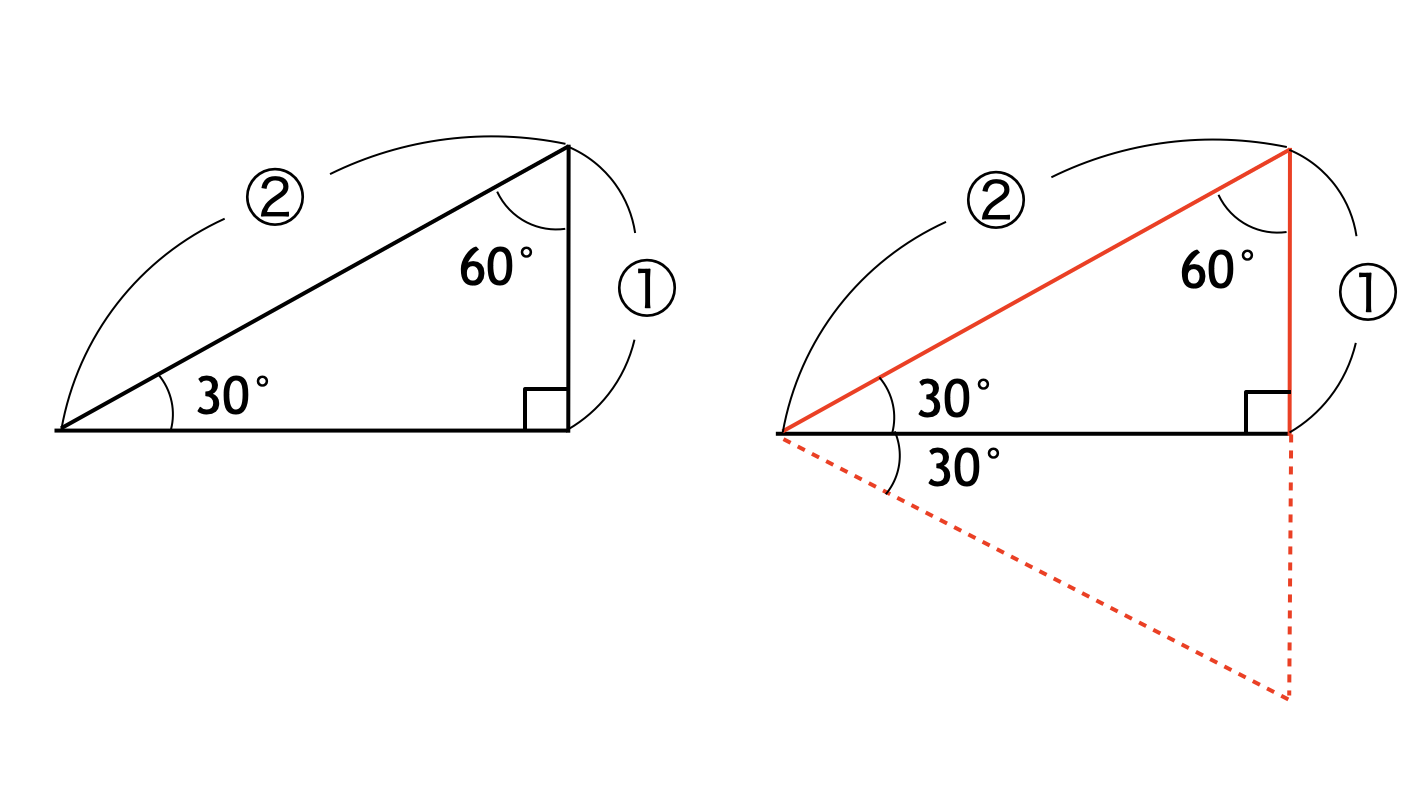
本問に戻ると、求める三角形の面積は、底辺が $10$ cm、高さが $5$ cm であることから、
$10 \times 5 \div 2 = 25$ cm²
です。
$30$° を挟む角を見たら、辺の比が $2 : 1$ の直角三角形を活用できないかと考えてみましょう。
そして、$30$° だけではなく $150$° でも、下図のように同様のことができます。
【さらなる話題】
数学 IA の三角比にも登場する考え方！
数学 IA の単元「図形の計量」では、$1$ つの内角が $\theta$ で、それを挟む $2$ 辺の長さが $a, b$ である三角形の面積 $S$ が、
$\displaystyle S = \frac{1}{2} ab \sin{\theta}$
であることを学びます。その証明方法は、まさに上の問題でやった論法と同じです。下図のように、三角形の頂点から対辺へ垂線を下ろすと、その長さは $a \sin{\theta}$ となります。
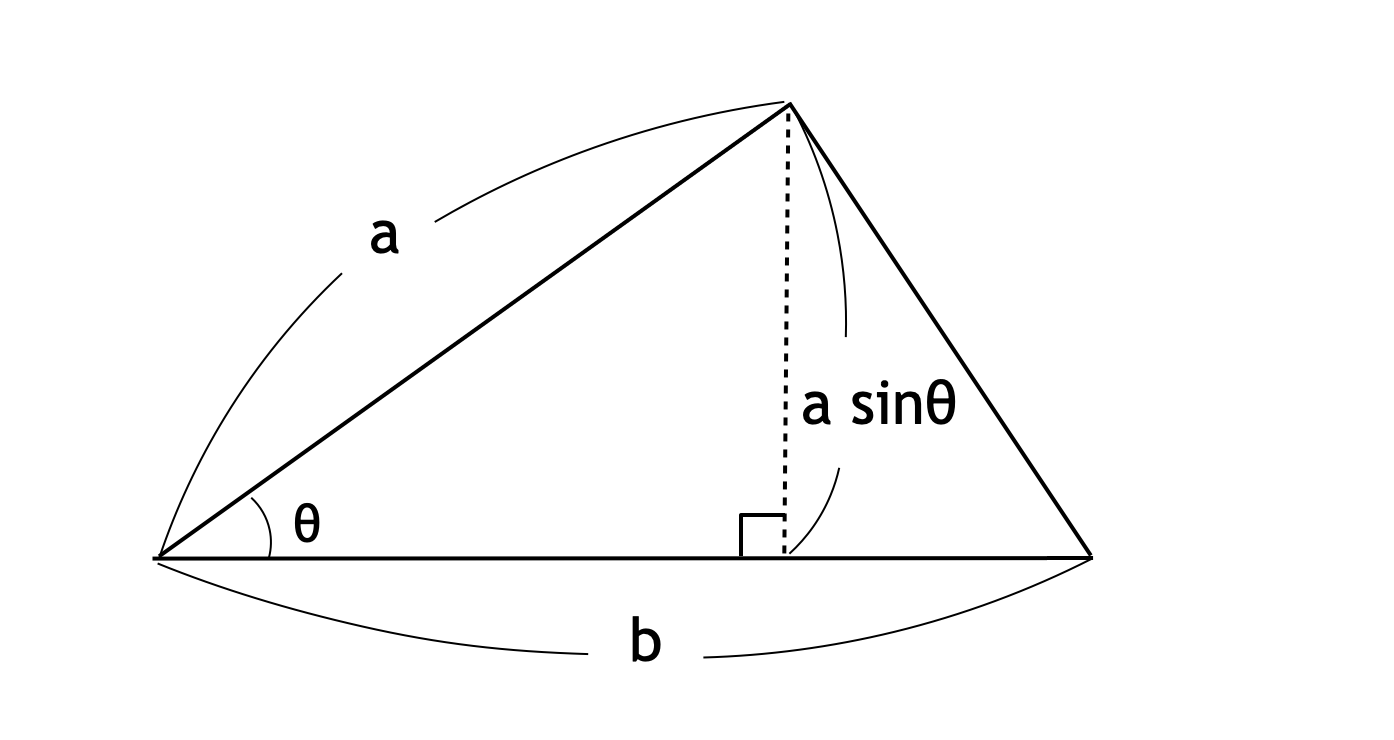
よって、求める三角形は、底辺の長さが $b$、高さが $a \sin{\theta}$ なので、面積は
$\displaystyle S = b \times (a \sin{\theta}) \div 2 = \frac{1}{2} ab \sin{\theta}$
と計算できます。
例題 8 は、数学 IA で学ぶ内容が、中学受験の算数の延長上にあることを示す例だといえます。
例題 9： ジグソーパズル (難易度 ★★☆☆☆)
次は、まるでジグソーパズルのように楽しめる問題です。
【問題文】
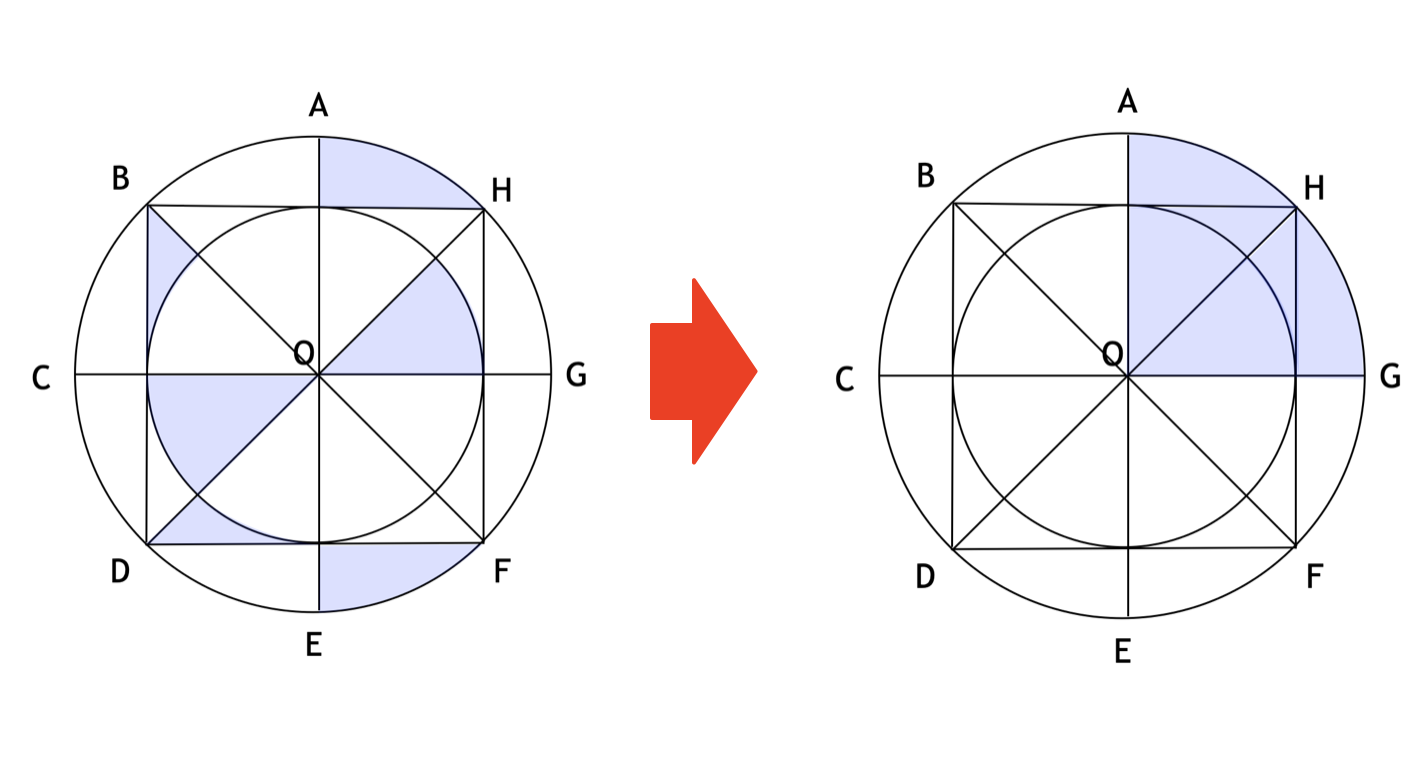
次の図で、点 A, B, C, D, E, F, G, H は点 O を中心とする円の周を $8$ 等分しています。OA の長さは $4$ cm です。
このとき、色のついた部分の面積を求めなさい。ただし、円周率は $3.14$ とします。
答え
$12.56$ cm²
解説
下図のように、色のついた部分を 1 箇所に集めてみましょう。中心角が $90$° の扇形となります。
よって、求める面積は、
$\displaystyle 4 \times 4 \times 3.14 \times \frac{90}{360} = 4 \times 3.14 = 12.56$ cm²
$3.14$ のかけ算の計算は、最後にまとめて実行することがポイントです。たとえば、
$8 \times 8 \times 3.14 + 5 \times 5 \times 3.14 + 4 \times 4 \times 3.14$
を計算したいとしましょう ($3$ 個の円の面積の和ですね)。次のように計算できます。$3.14$ の絡む複雑な計算がたった $1$ 回で済みますね。
$8 \times 8 \times 3.14 + 5 \times 5 \times 3.14 + 4 \times 4 \times 3.14$
$= 64 \times 3.14 + 25 \times 3.14 + 16 \times 3.14$
$= 105 \times 3.14$ (← $64 + 25 + 16 = 105$ より)
$= 329.7$
ここで、$64 \times 3.14$ や $25 \times 3.14$ や $16 \times 3.14$ の部分を先に計算すると、複雑な計算を三度も実行することになってしまいます。
なお、中1で学ぶ「文字と式」を知っている方でしたら、円周率 $\pi$ を用いるとより簡単です。
$8 \times 8 \times \pi + 5 \times 5 \times \pi + 4 \times 4 \times \pi$
$= 64\pi + 25\pi + 16\pi$
$= 105\pi$
と計算できます。最後に $\pi = 3.14$ を代入するのです。
例題 10： 十文字中 2023 年得意型算数 問 6 (難易度 ★★★☆☆)
それでは、実際に入試で出題された問題に挑戦してみましょう！ 十文字中 2023 年得意型算数の問 6 です。円周率は $3.14$ として計算する旨が表紙にあります。
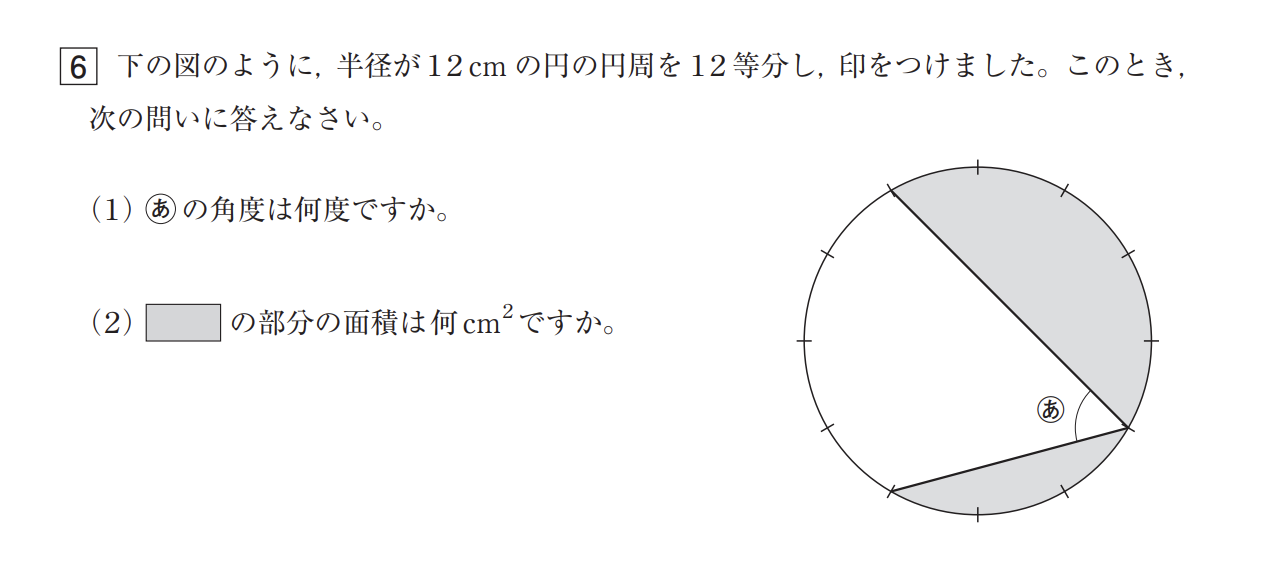
答え
(1) $60$°
(2) $193.44$ cm²
解説
(1)
下の図のように、円の中心を O とし、3 点 A, B, C を定めて、OA, OB, OC を結びます。この図形は、円周を $12$ 等分していて、弧 AC はそのうちの $5$ 個分を占めています。よって、
∠AOC $= 30 \times 5 = 150$°
です。同様に、弧 BC は円周 $12$ 等分のうちの $3$ 個分を占めているので、
∠BOC $= 30 \times 3 = 90$°
です。△OAC と △OBC はともに二等辺三角形なので、
- ∠OCA $= (180 - 150) \div 2 = 15$°
- ∠OCB $= (180 - 90) \div 2 = 45$
よって、角「あ」は、
$15 + 45 = 60$°
(2)
色のついた部分の面積を求めるためには、中心角が $150 + 90 = 240$° の扇形から、△OAC と △OBC の面積を引けばよいでしょう。まず、扇形の面積は
$\displaystyle 12 \times 12 \times 3.14 \times \frac{240}{360} = 301.44$ cm²
です。次に、△OBC の面積は
$12 \times 12 \div 2 = 72$ cm²
です。最後に、△OAC の面積は、下図を参考にして、
$12 \times 6 \div 2 = 36$ cm²
です。よって、求める面積は次のようになります。
$301.44 - (72 + 36) = 193.44$ cm²
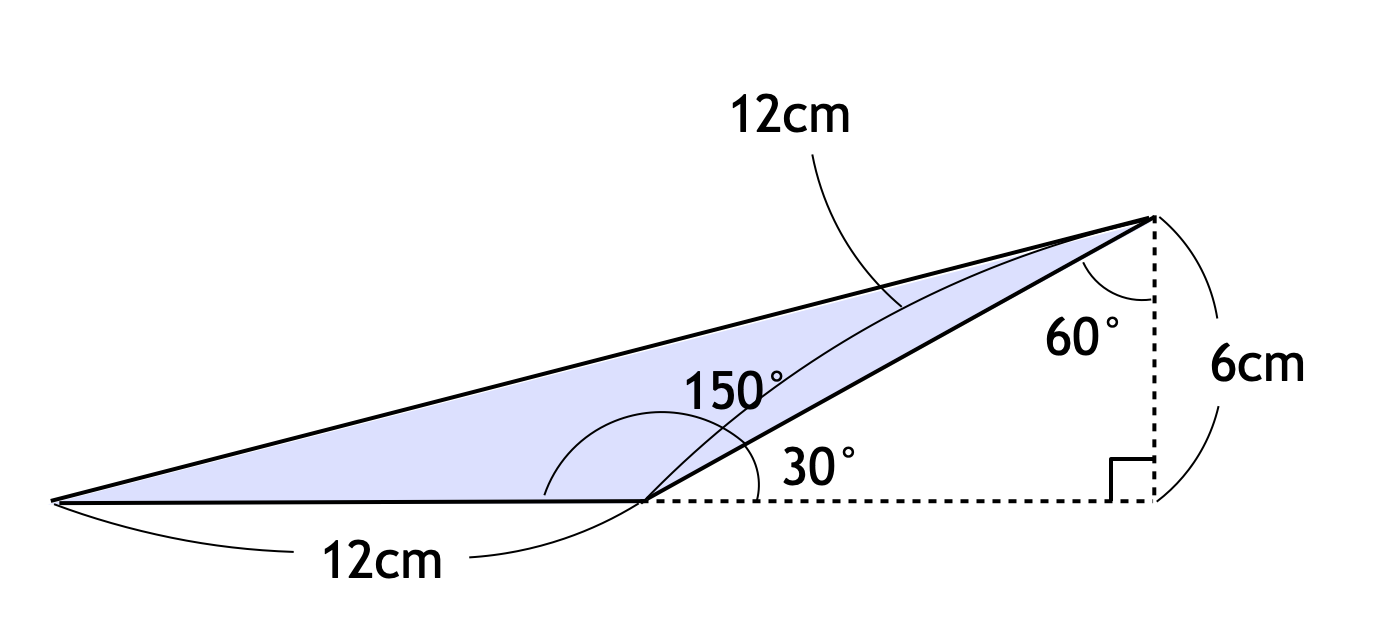
円周を $12$ 等分する構図の問題は、難関校では頻出です。その多くは、この問題のように、円の中心と円周上の点を結ぶことで解決できます。類題として
- 昭和学院秀英中 2023 年算数 問 3 (難易度 ★★☆☆☆)
- 関東学院中 2022 年算数 問 7 (難易度 ★★☆☆☆)
- 海城中 2021 年算数 問 1 (5) (難易度 ★★★☆☆)
- 豊島岡女子学園中 2021 年算数 問 2 (3) (難易度 ★★★☆☆)
- 中央大学附属横浜中 2019 年算数 問 1 (10) (難易度 ★★★☆☆)
- 市川中 2018 年算数 問 1 (5) (難易度 ★★★☆☆)
- 豊島岡女子学園中 2011 年算数 問 2 (4) (難易度 ★★★★☆)
などがあります。ぜひ、これらの問題も挑戦してみてください。
【さらなる話題】
(1) は、数学 IA の単元「図形の性質」を履修済みの方ならば、円周角の定理から直接求めることもできます。角「あ」は、円周を $12$ 等分したうちの $4$ 個分の円弧に対する円周角であることに留意しましょう。円周全体に対応する円周角は $180$ なので、
$\displaystyle 180 \times \frac{4}{12} = 60$°
と求められます。
4 章： 特殊算 〜 方程式と一次関数！ 〜
中学受験の算数と言えば、つるかめ算のような特殊算を思い浮かべる人も少なくないと思います。大人になってみれば、これらの多くは $x$ を使った方程式を立てることで解くことができます。しかしながら、特殊算は特殊算なりに学べることがたくさんあります。それらを見ていきましょう。
例題 11： 和差算 (難易度 ★★☆☆☆)
まずは、特殊算の先頭バッターとして紹介されることの多い和差算です11！
【問題文】
高橋くんと青木くんは、合計で $20$ 個のりんごを分け合いました。高橋くんは青木くんよりも $6$ 個多くのりんごをとりました。高橋くんと青木くんはそれぞれ何個ずつりんごをとったでしょうか。
答え
高橋くん： $13$ 個
青木くん： $7$ 個
解説
高橋くんと青木くんのとったりんごの個数を線分図で表してみましょう。下図のようになります。
個数を青木くんに揃えるために、高橋くんの取り分を $6$ 個減らしてみましょう。そうすると、合計は
$20 - 6 = 14$ 個
となります。よって、青木くんの取り分は、
$14 \div 2 = 7$ 個
高橋くんの取り分は、青木くんよりも $6$ 個多いので、
$7 + 6 = 13$ 個
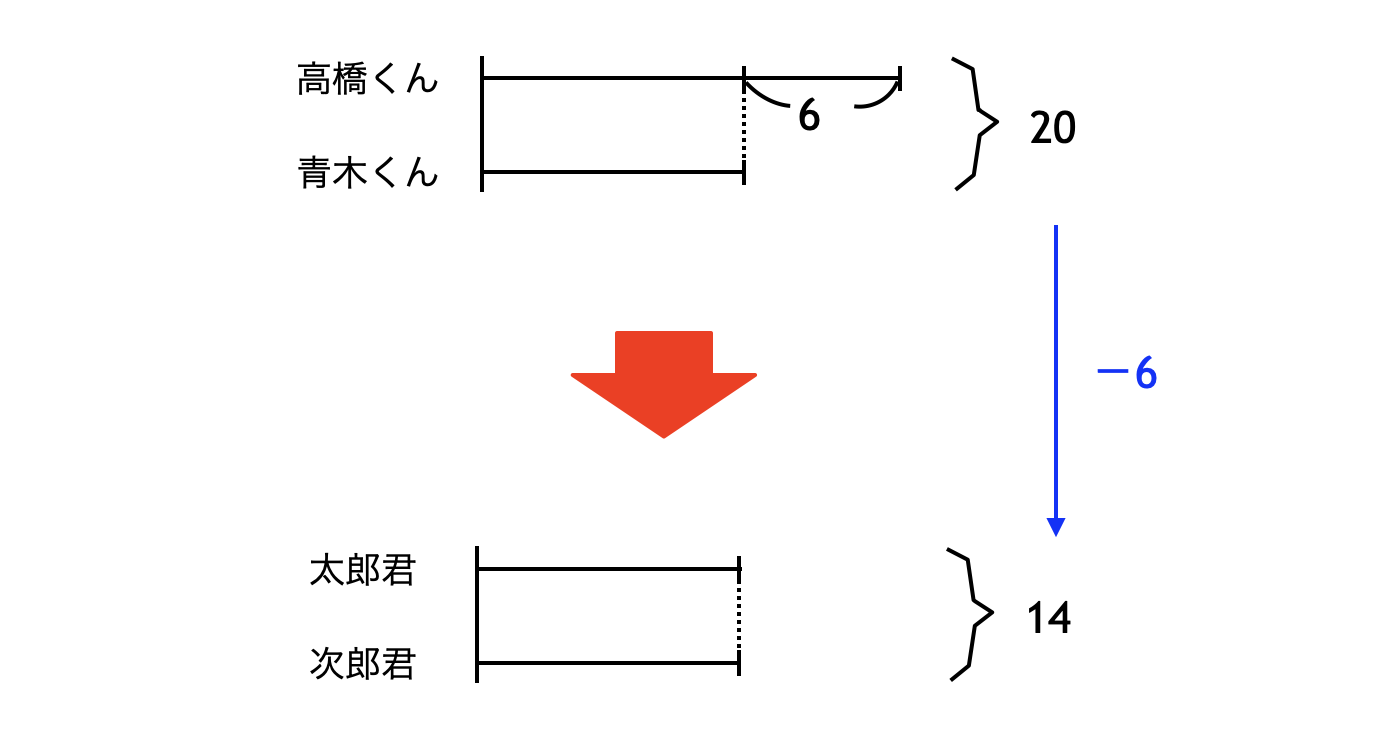
特殊算では、問題の情報を上手に整理する技能が問われます。整理する方法としては、どんな方法を使ってもよいのですが、中学受験の指導においては、線分図や面積図などで表すことが多いですね。
【さらなる話題】
算数や数学のセンスを磨くコツとして、問題を少し変えて解いてみることは有効です。たとえば、上の問題文を少し変更して、「高橋くんは青木くんよりも $7$ 個多い」という問題を考えてみましょう。そうすると、高橋くんの取り分を $7$ 個減らしたときに、
$20 - 7 = 13$ 個
となります。しかし、これは奇数ですので、$2$ つに分けることができません。つまり、高橋くんの取り分が青木くんよりも $7$ 個多くなることは起こり得ないとわかりました。
そうなると、高橋くんと青木くんとで $20$ 個のりんごを分け合ったとき、
(高橋くんの取り分) - (青木くんの取り分)
の値として考えられるものをすべて求めてみたくなりますね。ぜひ考えてみてください！
クイズの答え
一般に、高橋くんと青木くんの取り分の合計値を $N$ としましょう。
- $N$ が偶数のとき： (高橋くんの取り分) - (青木くんの取り分) は、$-N$ 以上 $N$ 以下の偶数値をすべて取り得ます
- $N$ が奇数のとき： (高橋くんの取り分) - (青木くんの取り分) は、$-N$ 以上 $N$ 以下の奇数値をすべて取り得ます
例題 12： 分配算 (難易度 ★★☆☆☆)
上の例題では、「和」と「差」という情報を可視化しました。今度は「倍」という情報を可視化してみましょう。
【問題文】
三角形 ABC で、∠A の大きさは ∠B の大きさの $3$ 倍であり、∠C の大きさは ∠B の大きさの $2$ 倍よりも $30$° 大きい。
∠A は何度でしょうか。
答え
解説
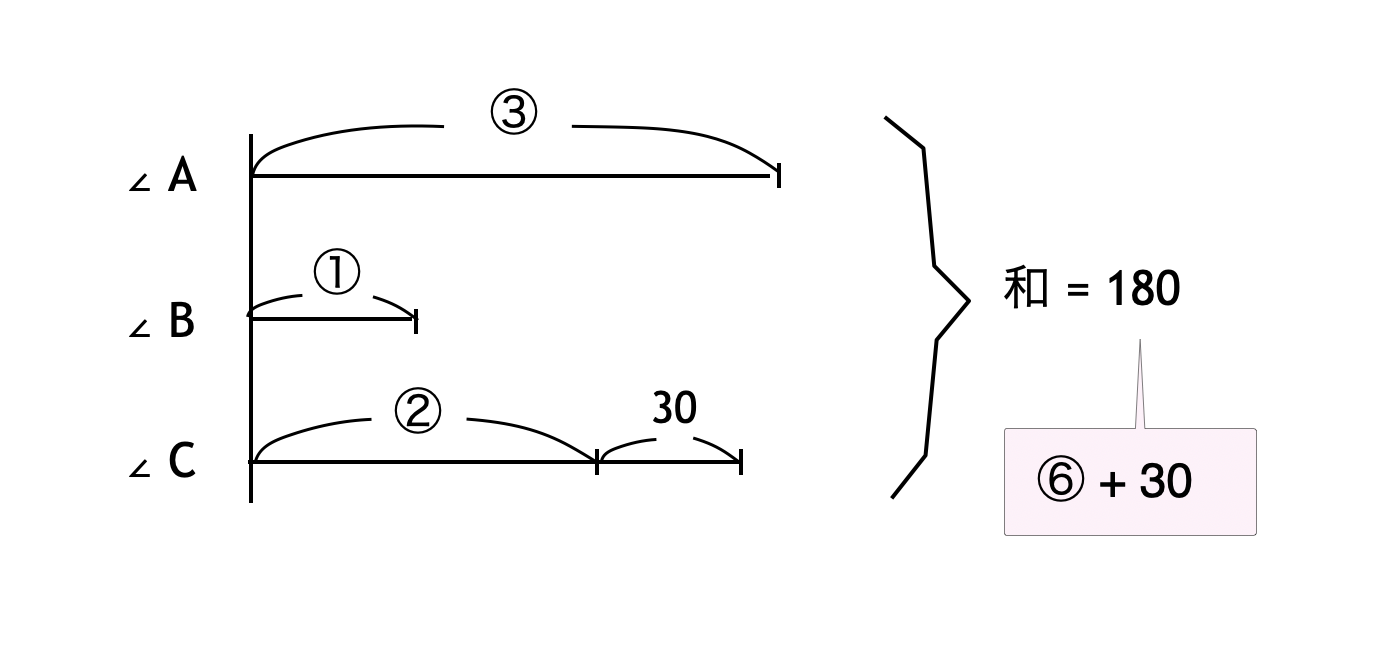
以上の情報を線分図として整理すると、下図のようになります。
∠A, B, C の和は ⑥ $+ 30$° と表せることが分かりました。よって、和が $180$° であることから、
⑥ $= 150$°
となります。⑥ は「① が $6$ 個分である」ことを表しているのですから、
① $= 150 \div 6 = 25$°
となります。よって、∠A の大きさは ③ ですので、
$25 \times 3 = 75$°
です。
いくつかポイントがあります。まず、問題文の条件を適切に言い換える力が問われています。∠A, B, C が三角形の角であることを「和が $180$°」と言い換えましょう。このような言い換えは、難関校になると求められるようになっていきます。
今回の問題では、「A が B の $3$ 倍」という情報を表すために、B を ① とおいて A を ③ とおきました。ここで、何を ① とおけばよいかが分からないという声をよく聞きます。
どうしても分からない場合は、A と B のどちらの方が小さいかを考えてみましょう。小さい方を ① とおくことで上手くいくことが多いです ($0.5$ 倍などのような場合は例外です)。
【さらなる話題】
大人にとっては、次のように方程式を用いて解くのが自然かもしれません。
∠B の大きさを $x$ とおくと，
- ∠A の大きさは、$3x$
- ∠C の大きさは、$2x + 30$
となります。∠A, B, C の和が $180$ 度であることから，
$(3x) + x + (2x + 30) = 180$
となります。これを解くと、$x = 25$ となります。
子どもに中学受験の算数を教えている大人は、「方程式で簡単に解ける問題なのに特殊な方法を要求される......」などと複雑な感情を抱える方も多いかもしれません。
しかし、実は、小学生向けの解法も本質的にまったく一緒です。$x$ を ① と表していて、$3x$ を ③ と表しているのです。方程式を使いこなせる大人にとって、子ども向けにアレンジして教えるのは容易いはずです。
例題 13： 年齢算 (難易度 ★★☆☆☆)
例題 12 では「和が一定」($3$ つの角度の和が $180$°) という情報を扱いました。今回の年齢算では「差が一定」という情報を扱います！
【問題文】
現在、父は $35$ 歳、子どもの年齢は $3$ 歳です。父の年齢が子どもの年齢の $5$ 倍になるのは何年後でしょうか。
答え
$5$ 年後
解説
この問題のポイントは、「何年経っても父と子どもの年齢差は $32$ 歳のままで一定である」ことです。
具体的に式を用いて表してみましょう。$□$ 年後に父の年齢が子どもの年齢の $5$ 倍になるとします。このとき、$□$ 年後の子どもの年齢を $①$ とすると、父の年齢は $⑤$ と表せます。よって、
- $35 + □ = ⑤$
- $3 + □ = ①$
と表せます。これらの差をとると、次のようになります。
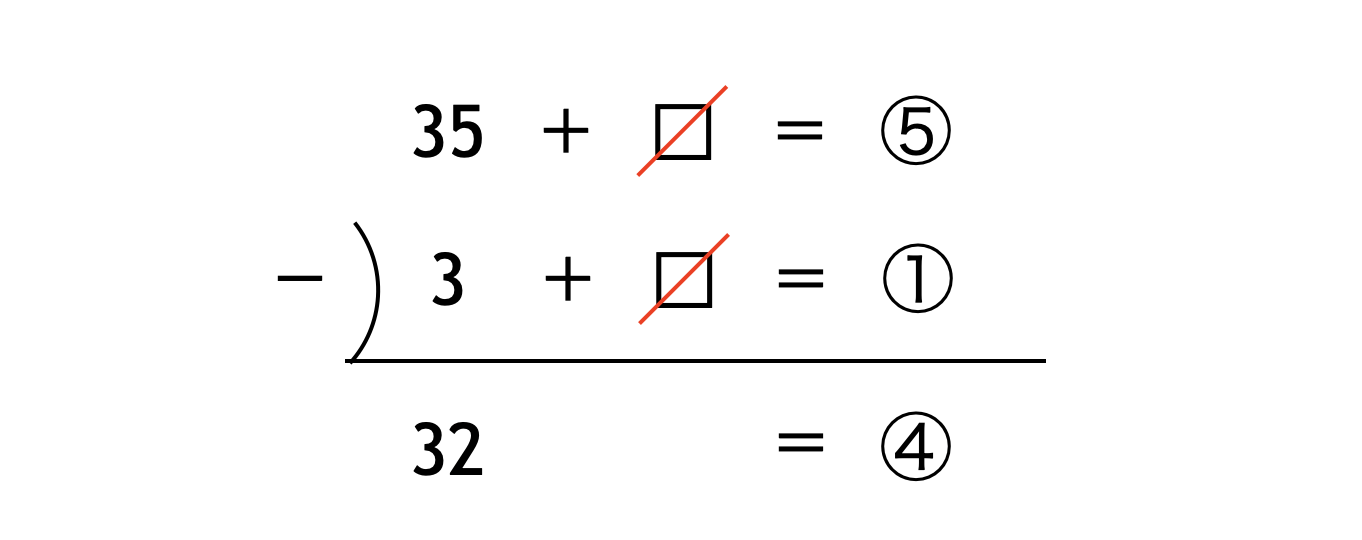
よって、$④ = 32$ より、
$① = 32 \div 4 = 8$
子どもの年齢が $3$ 歳から $8$ 歳になっていることから、
$□ = 8 - 3 = 5$ 年後
と求められます。
年齢算の難しいパターンとしては、例題 13 のような「1 人 vs. 1 人」を発展させて、「1 人 vs. 2 人」や「2 人 vs. 3 人」などのように、複数人同士を比較する問題が挙げられます。その場合「差が一定」という性質は壊れることに注意しましょう。
しかし、その場合であっても「ある値」が一定になります。ぜひ考えてみてください！
例題 14： つるかめ算 (難易度 ★★☆☆☆)
いよいよ、中受算数の顔ともいうべきつるかめ算を考えます！
【問題文】
つるは足が $2$ 本、かめは足が $4$ 本あります。
つるとかめが合わせて $100$ います。足の本数が合計 $326$ 本であるとき、つるとかめがそれぞれ何頭ずついるでしょうか。
答え
つる：$37$ 頭、かめ：$63$ 頭
解説
$100$ 頭すべてがつるであるとき (かめが $0$ 頭であるとき)、足の本数は $2 \times 100 = 200$ 本となります。次に、かめが $1$ 頭であるとき、足の本数は $2 \times 99 + 4 \times 1 = 202$ 本となります。
同様に、かめが $2, 3, 4, \dots, 100$ 頭でいる場合を表にまとめると、次のようになります。
| かめの頭数 | $0$ | $1$ | $2$ | $3$ | $\dots$ | $100$ |
|---|---|---|---|---|---|---|
| 足の本数 | $200$ | $202$ | $204$ | $206$ | $\dots$ | $400$ |
かめが $1$ 頭増えるごとに、足の本数が $2$ 本ずつ増えることに着目します。よって、「かめがいない場合」と比べて足の本数が $326 - 200 = 126$ 本増える必要があることから、かめの頭数は
$126 \div 2 = 63$ 頭
と求められます。つるは $100 - 63 = 37$ 頭です。
つるかめ算は、「当てずっぽう」で答えを当てる気持ちでやるとわかりやすいかもしれません。たとえば、かめが $10$ 頭と決め打ちすると、足の本数は $2 \times (100 - 10) + 4 \times 10 = 220$ 本です。
目標の $326$ 本よりも少ないので、かめを大きく増やしてみよう......ということで、かめが $60$ 頭であると決め打ちすると、足の本数は $2 \times (100 - 50) + 4 \times 50 = 300$ 本です。
まだ少し足りないので、かめをさらに増やしたいのですが......闇雲に増やすよりも、良い方法があります。そもそも、かめが $1$ 頭増えると、足が $2$ 本増えるのです (つるかめ算のよく知られた事実)。
よって、足の本数が $300$ 本から $326$ 本へと増えるためには、かめが
$(326 - 300) \div 2 = 13$ 頭
増える必要があります。つまり、かめは $50 + 13 = 63$ 頭です。
上に書いたような方法は単なる当てずっぽうだと思うかもしれません。しかし、実は本質的な解法なのです。算数で登場する文章題は、ほとんどの場合、「かめが増えるときの足の本数の増え方は一定である」というような性質が成立します。
よって、求めたい値を 2 つ決め打ちすれば、求めたい値を特定できるという裏技が成立するのです！！！ その決め打ちする $2$ つの値として、$0$ (すべて鶴である場合) と $1$ (かめが $1$ 頭増えた場合) を採用するのは自然なことでしょう。これがつるかめ算の正体です！！！
【さらなる話題】
つるかめ算は、中2で学ぶ「一次関数」の応用と見ることができます。上の問題 14 で、かめの頭数を $x$ 頭、足の本数の合計を $y$ 本としたとき、$y$ を $x$ で表します。
さて、一次関数を求める代表的な方法として「切片」と「傾き」を求める方法があります。一次関数を $y = ax + b$ と表したとき、切片は $a$、傾きは $b$ です。問題 14 では、
- 切片は「かめが $0$ 頭のときの足の本数」なので、$2 \times 100 = 200$ です
- 傾きは「かめが $1$ 頭増えるごとに足の本数は $2$ 本ずつ増える」ので、$2$ です。
よって、求める一次関数は
$y = 2x + 200$
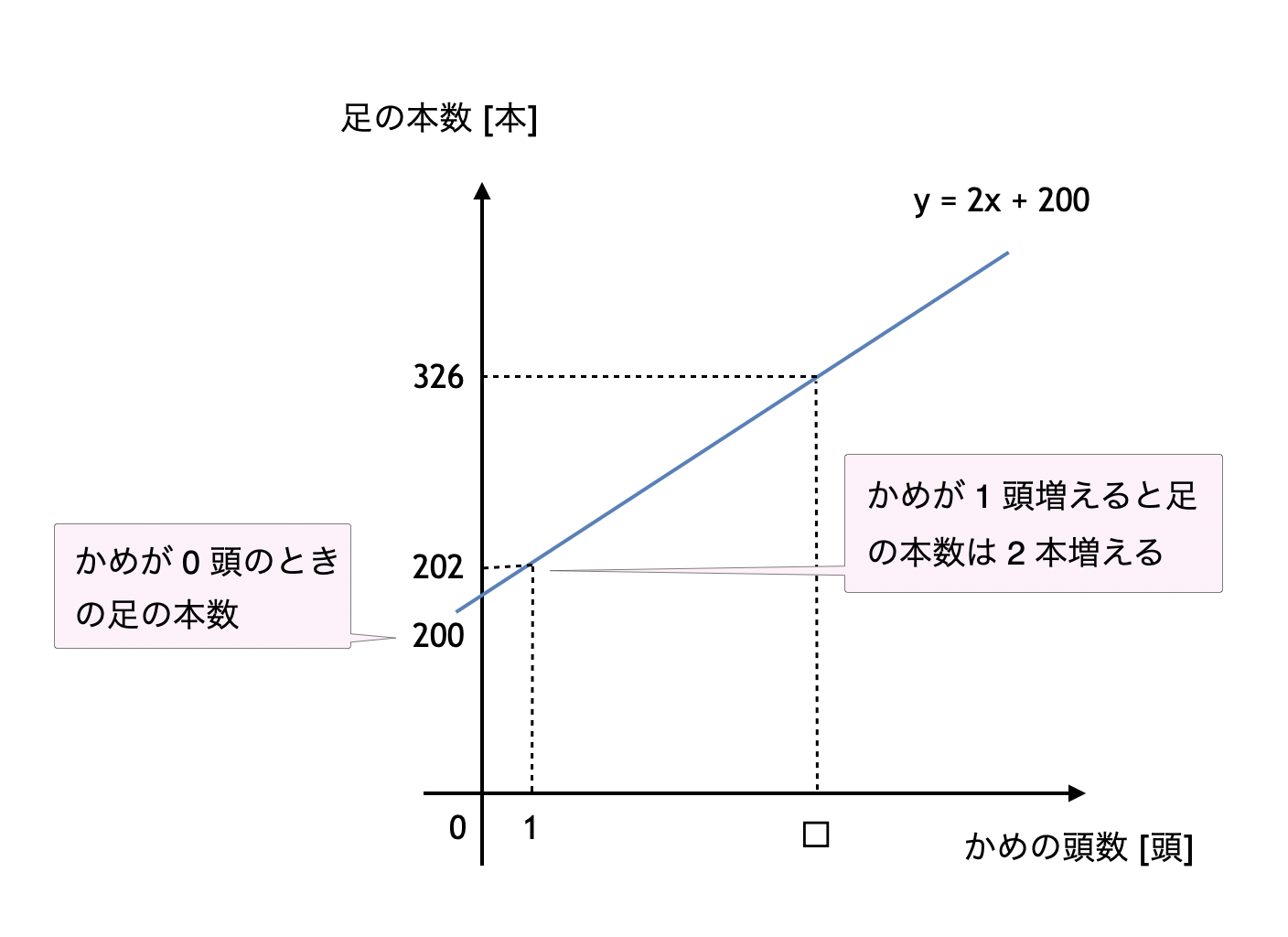
$y = 326$ となるときの $x$ を求めると、
$326 = 2x + 200$
$x = 63$
となります。よって、かめは $63$ 頭です。
さて、よく見るとこの一次関数を用いた解法は「つるかめ算の算法」そのものになっています！ 個人的には、つるかめ算を単に「$2$ 種類のものの合計個数と合計値から何個ずつかを求める方法」と捉えるのはもったいないと思います。それよりも、切片と傾きを求めることで答えを求める方法と捉えた方が適用範囲が広くなります。
例題 15： 差集め算 (難易度 ★★☆☆☆)
差集め算も、中受算数の考え方を支える大切なものです。旅人算なども差集め算の応用と言えます。
【問題文】
みかんが何個かあります。これを何人かの子どもたちに配ります。
子ども $1$ 人につき $3$ 個ずつ配ると、みかんは $31$ 個余ります。子ども $1$ 人につき $5$ 個ずつ配ると、みかんは $5$ 個足りませんでした。
子どもは何人いるでしょうか。
答え
解説
みかんを $3$ 個ずつ配って全員に配り切った状態と、みかんを $5$ 個ずつ配って全員に配り切った状態とで、配ったみかんの個数の差がどのように広がっていくかを考えましょう。
- 子ども $1$ 人のときは、$5 - 3 = 2$ 個の差
- 子ども $2$ 人のときは $10 - 6 = 4$ 個の差
- 子ども $3$ 人のときは $15 - 9 = 6$ 個の差
- ...
というように、子どもが $1$ 人増えるごとに、配るみかんの個数の差は $2$ 個ずつ広がっていきます。
ここで、みかんを子どもたちに配った状態を整理すると下図のようになります (子どもの人数を □ 人としています)。みかんを $3$ 個ずつ配って全員に配り切った状態と、みかんを $5$ 個ずつ配って全員に配り切った状態とで、
$31 + 5 = 36$ 個
の差があることが分かります。
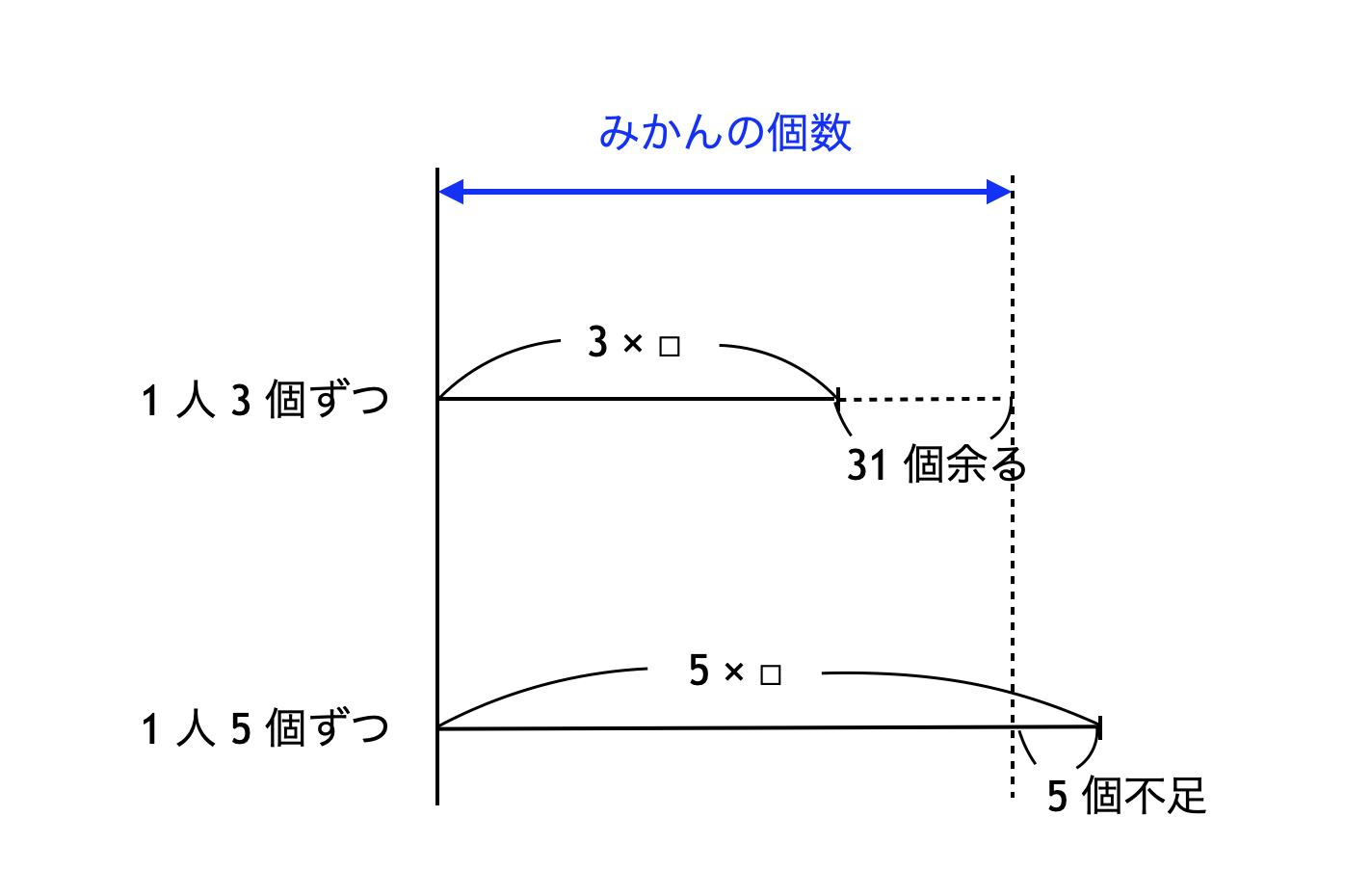
よって、子どもの人数は
$36 \div 2 = 18$ 人
と求められます。
「みかんが余った」という情報や、「みかんが不足した」という情報を整理するのが難しいと思います。これは慣れるまで考え続けるしかないでしょう。何度もイメージを繰り返して、イメージ記憶を定着させていきましょう。
例題 16： ビリヤード (難易度 ★★☆☆☆)
中学受験の算数では、比という概念が中心的な役割を果たします。比を題材とした次の問題を解いてみましょう12。
【問題文】
次の図のように、点 A に配置されたボールを適切な方向へ発射して、壁で反射させて点 B に到達するようにしたいとします。ボールが壁で反射するとき、入射角と反射角は等しいとします。
このとき、次の図の $□$ にあてはまる数を答えなさい。
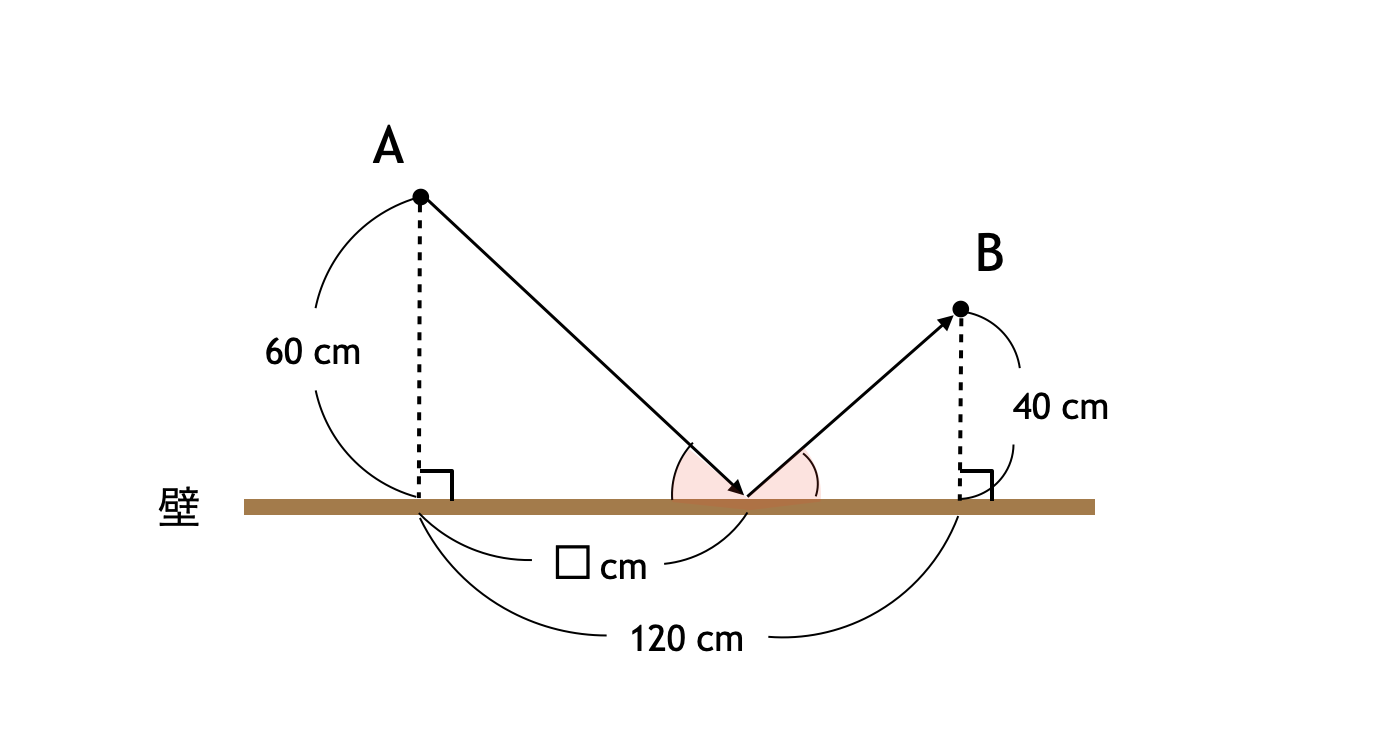
答え
解説
ボールが壁に反射するときの入射角と反射角が等しいことから、壁に反射する前後で次のことが成立します。
(ボールが縦方向に動く長さの比) $=$ (ボールが横方向に動く長さの比)
ボールが壁に反射する前後で、縦方向に動く長さの比は $60 : 40 = 3 : 2$ なので、横方向に動く長さの比も $3 : 2$ となります。このことから、
- ボールが壁に反射する前に横方向に動く長さ $= ③$ [cm]
- ボールが壁に反射した後に横方向に動く長さ $= ②$ [cm]
とおけます (下図)。
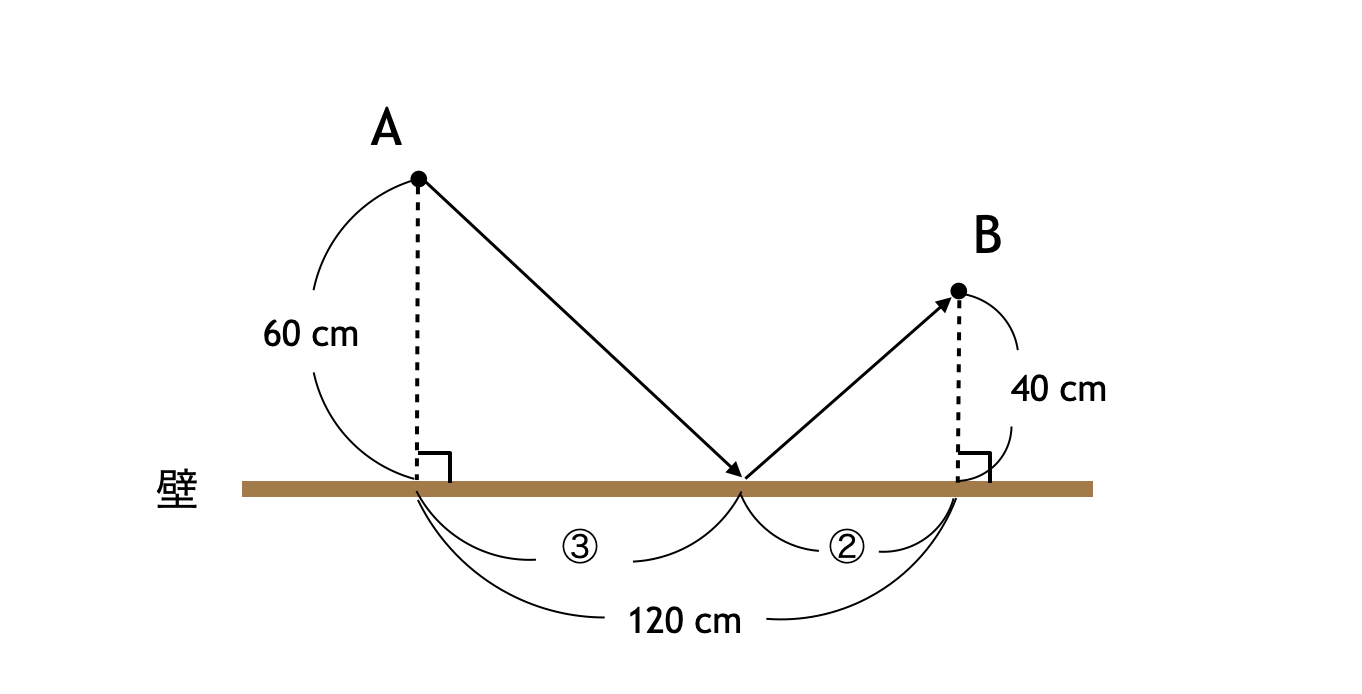
よって、$⑤ = 120$ となるので、求める長さは
$\displaystyle ③ = 120 \times \frac{3}{5} = 72$ [cm]
この問題では、「$120$ という数量を $3 : 2$ に分ける」という処理をしました。このように、ある数量をある比で分けることを比例配分といいます。
一般に、ある数量を $a : b$ に分配するとき、それぞれの数量は
- $\displaystyle (ある数量) \times \frac{a}{a + b}$
- $\displaystyle (ある数量) \times \frac{b}{a + b}$
となります。
【さらなる話題】
内分点の公式
数学 IIB の単元「図形と方程式」では、内分点の公式が登場します。$m, n > 0$ のとき、$2$ 点 $(x_1, y_1), (x_2, y_2)$ を $m : n$ に内分する点の座標は、次のようになります。
$\displaystyle \bigl(\frac{nx_1 + mx_2}{m + n}, \frac{ny_1 + my_2}{m + n}\bigr)$
このことは、比例配分の計算から導くことができます。
例題 17： 仕事算 (難易度 ★★☆☆☆)
続いて、実用的にも「人月」などを考えるときに登場するような、重要な問題を解いてみましょう！
【問題文】
ある仕事をするのに高橋君は $14$ 日、青木君は $21$ 日かかります。
$2$ 人で一緒にこの仕事をはじめましたが、途中で高橋君が何日か休んだため、仕事を仕上げるのに $12$ 日かかりました。高橋君は何日間休んだでしょうか。
答え
解説
$14$ と $21$ の最小公倍数は $42$ です。そこで、全体の仕事量を $㊷$ と置いてみましょう。このとき、
- 高橋君の $1$ 日あたりの仕事量： $㊷ \div 14 = ③$
- 青木君の $1$ 日あたりの仕事量： $㊷ \div 21 = ②$
と求められます。
さて、全体の仕事のうち、青木君がした分の仕事量は
$② \times 12 = ㉔$
よって、高橋君がした分の仕事量は $㊷ - ㉔ = ⑱$ なので、高橋君が働いた日数は
$⑱ \div ③ = 6$ 日
です。高橋君が休んだ日数は
$12 - 6 = 6$ 日
と求められます。
ここで、逆比という概念を紹介します。
「仕事に要する日数」と「$1$ 日あたりの仕事量」は反比例の関係
にあります。「仕事に要する日数」が $2$ 倍になると、「$1$ 日あたりの仕事量」は $\frac{1}{2}$ 倍になるのです。
さて、今回は高橋君と青木君について、次のことが成り立っていました。
高橋君の仕事に要する日数 $:$ 青木君の仕事に要する日数 $= 2 : 3$
このとき、「仕事に要する日数」と「$1$ 日あたりの仕事量」は反比例であることに着目すると、次のようになります。
高橋君の $1$ 日あたりの仕事量 $:$ 青木君の $1$ 日あたりの仕事量 $\displaystyle= \frac{1}{2} : \frac{1}{3} = 3 : 2$
このように、反比例の関係にある変量の比は、もとの変量の比の逆になります。これを逆比とよびます。中学受験の算数や理科では、逆比の考え方を活用できる問題が数多く登場します！
例題 18： 愛光中 2023 年算数 問 2 (難易度 ★★★☆☆)
それでは 4 章の集大成として、実際の入試問題を解いてみましょう！
答え
(1) ① $12$ 人 ② $8$ 人
(2) $12$ 回
解説
いろんな方法が考えられます。ここでは一例を示します。
(1)
操作②を実行しても、袋の中の球の個数が変わらないことに着目しましょう。一方、操作①によって、袋の中の球の個数は $5$ 個減ります。ここで、
- 初期状態は、球の個数の合計が $150 + 100 = 250$ 個
- すべての操作後は、球の個数の合計が $106 + 84 = 190$ 個
であることから、すべての操作によって、球の個数は $250 - 190 = 60$ 個減っています。よって、操作①は
$60 \div 5 = 12$ 回
実行されたと求められます。さて、初期状態から操作①を $12$ 回実行すると、
赤球：$114$ 個、白球：$76$ 個
となります。よって、すべての操作後の赤球の個数が $106$ 個であることから、操作②は
$(114 - 106) \div 1 = 8$ 回
実行されたと求められます。
(2)
つるかめ算の考え方を応用しましょう。まず、操作②の実行回数を $0$ 回とすると、
赤玉：$36$ 個、白球 $24$ 個
となります。この差は $12$ 個です。次に、操作②の実行回数を $1$ 回とすると、
赤玉：$38$ 個、白球 $27$ 個
となります。この差は $11$ 個です。
よって、操作②の実行回数が $1$ 回増えるごとに、「赤玉の個数 - 白球の個数」は $12 - 11 = 1$ ずつ減っていくことが分かりました。赤玉と白球の個数が等しくなるための操作②の実行回数は
$12 \div 1 = 12$ 回
と求められます。
つるかめ算を「切片と傾きから求めたい値を求める方法」と捉えると、とても汎用性が強い方法であることがわかりますね！
5 章： 規則性 〜 法則を見つける！ 〜
中学受験の算数では、規則性を見出して、それを活用して問題を解くこともしばしば要求されます。このような、法則を発見するという営みは、プログラミング的思考の根幹を支えるものです。
例題 19： 循環小数 (難易度 ★★☆☆☆)
易しい問題から始めましょう！
【問題文】
分数 $\displaystyle \frac{1}{7}$ を小数で表したときの、小数第 $100$ 位の数字はなんでしょうか。
答え
解説
分数 $\displaystyle \frac{1}{7}$ を小数に直すと、次のようになります。
$\displaystyle \frac{1}{7} = 0.142857142857142857\dots$
小数第 $1$ から順に、$1, 4, 2, 8, 5, 7$ ($6$ 個あります) を繰り返すことが見て取れます。よって、
$100 \div 6 = 16$ あまり $4$
より、$\displaystyle \frac{1}{7}$ を表す小数を第 $100$ 位まで書いたとき、$1, 4, 2, 8, 5, 7$ を $16$ 回繰り返したのちに、$4$ 個の数字が続きます。
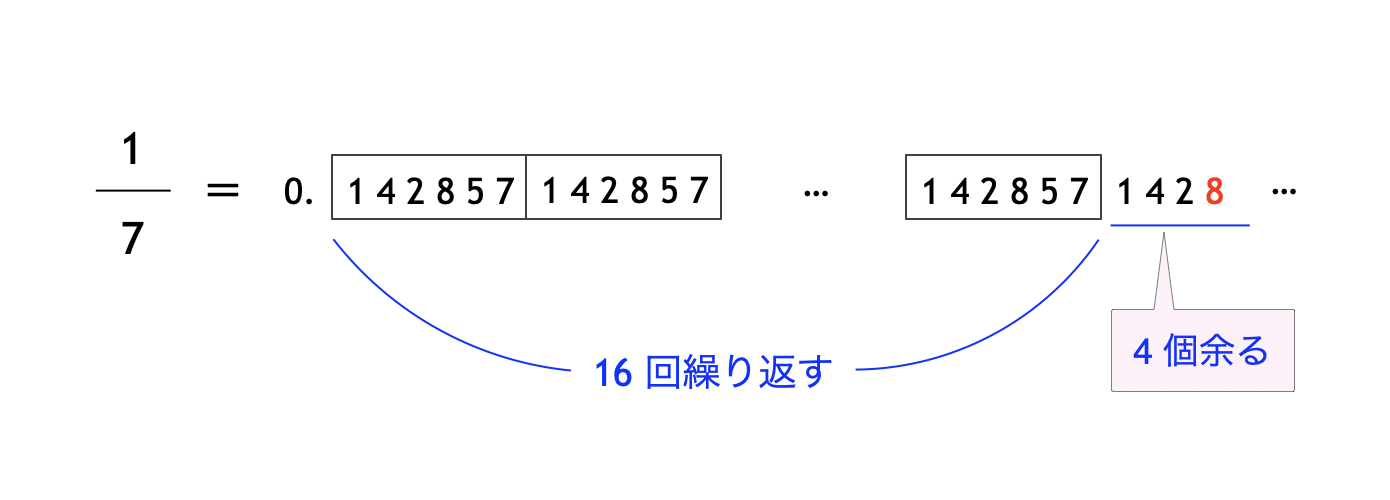
よって、$\displaystyle \frac{1}{7}$ を小数で表したときの、小数第 $100$ 位の数字は、$1, 4, 2, 8, 5, 7$ の $4$ 番目の $8$ です。
規則性の問題では、「周期的に並ぶことを見抜く」というタイプのものが多く見られます。
周期性を利用する方法については、例題 4： 曜日算でも登場しましたね。
【さらなる話題】
一般に、$m, n$ を正の整数として、分数 $\displaystyle \frac{n}{m}$ を小数にすると、かならず循環小数になります。
例題 20： パスカルの三角形 1 (難易度 ★★★☆☆)
次に、パスカルの三角形という有名な題材を取り上げます！
【問題文】
次の図のように、整数が規則的に並んでいます。$12$ 行目の数をすべて足すといくつになりますか。
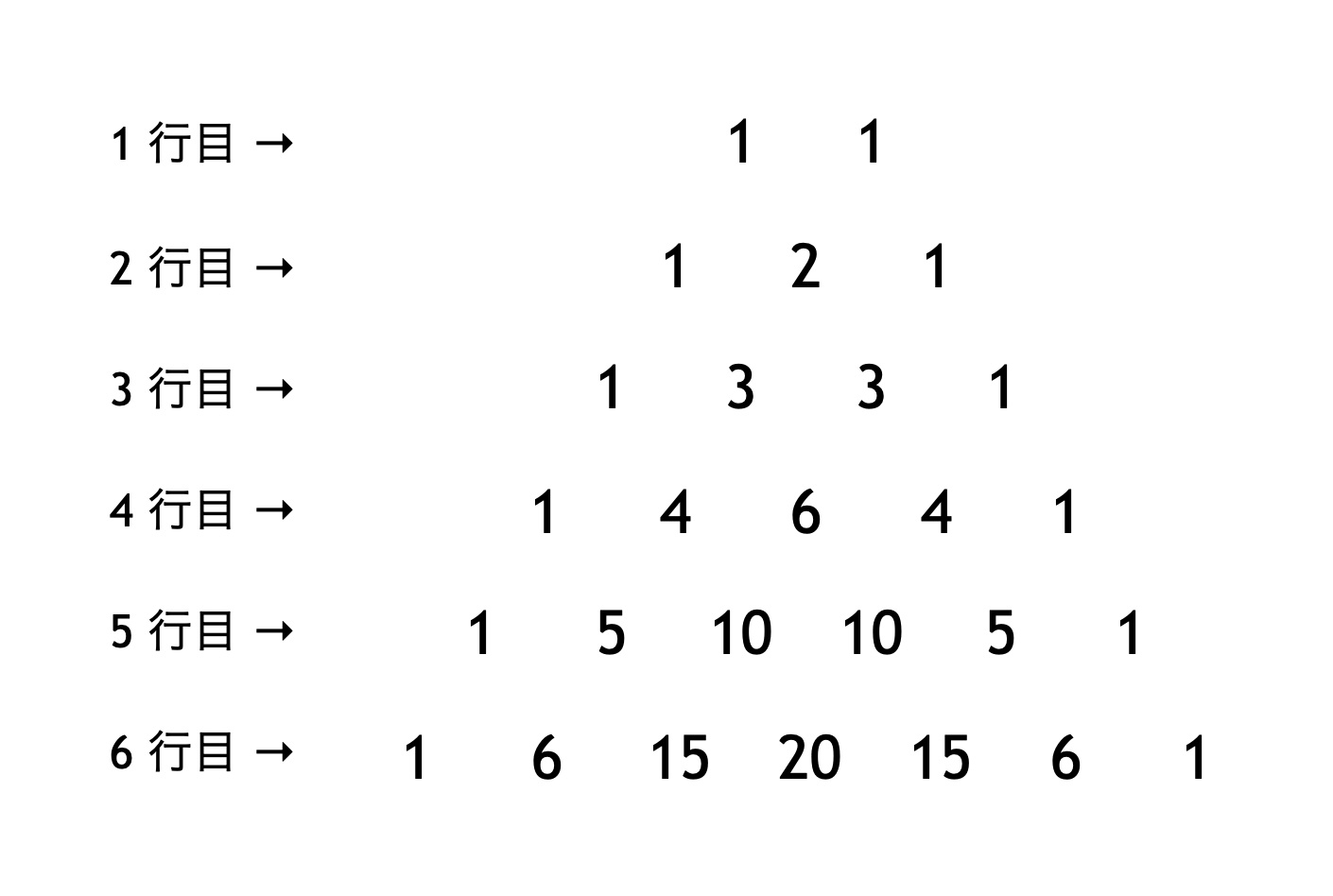
答え
解説
$1, 2, 3, \dots$ 行目の数の和を実際に計算してみましょう！ 次のようになります。
- $1$ 行目：$1 + 1 = 2$
- $2$ 行目：$1 + 2 + 1 = 4$
- $3$ 行目：$1 + 3 + 3 + 1 = 8$
- $4$ 行目：$1 + 4 + 6 + 4 + 1 = 16$
- $5$ 行目：$1 + 5 + 10 + 10 + 5 + 1 = 32$
- $\dots$
となります。行が増えるごとに、$2$ 倍していることが見て取れます。さらにいえば、一般に
$□$ 行目の数の和は、$2$ を $□$ 個かけた値である
ことが分かります。よって、$12$ 行目の数の和は
$2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 4096$
と求められます。
問題の手がかりを掴むのに苦心するときは、小さい部分について手を動かしてみることが大切です。
今回の問題では、いきなり $12$ 行目を考えることは難しいため、$1, 2, 3, 4, 5$ 行目などを考えます。そうすることで、規則性が見つかり、$□$ 行目の性質を予想できるようになります。
【さらなる話題】
今回の問題の数の並びはパスカルの三角形と呼ばれるものです。実は二項係数を用いて、次のように表されることが知られています。
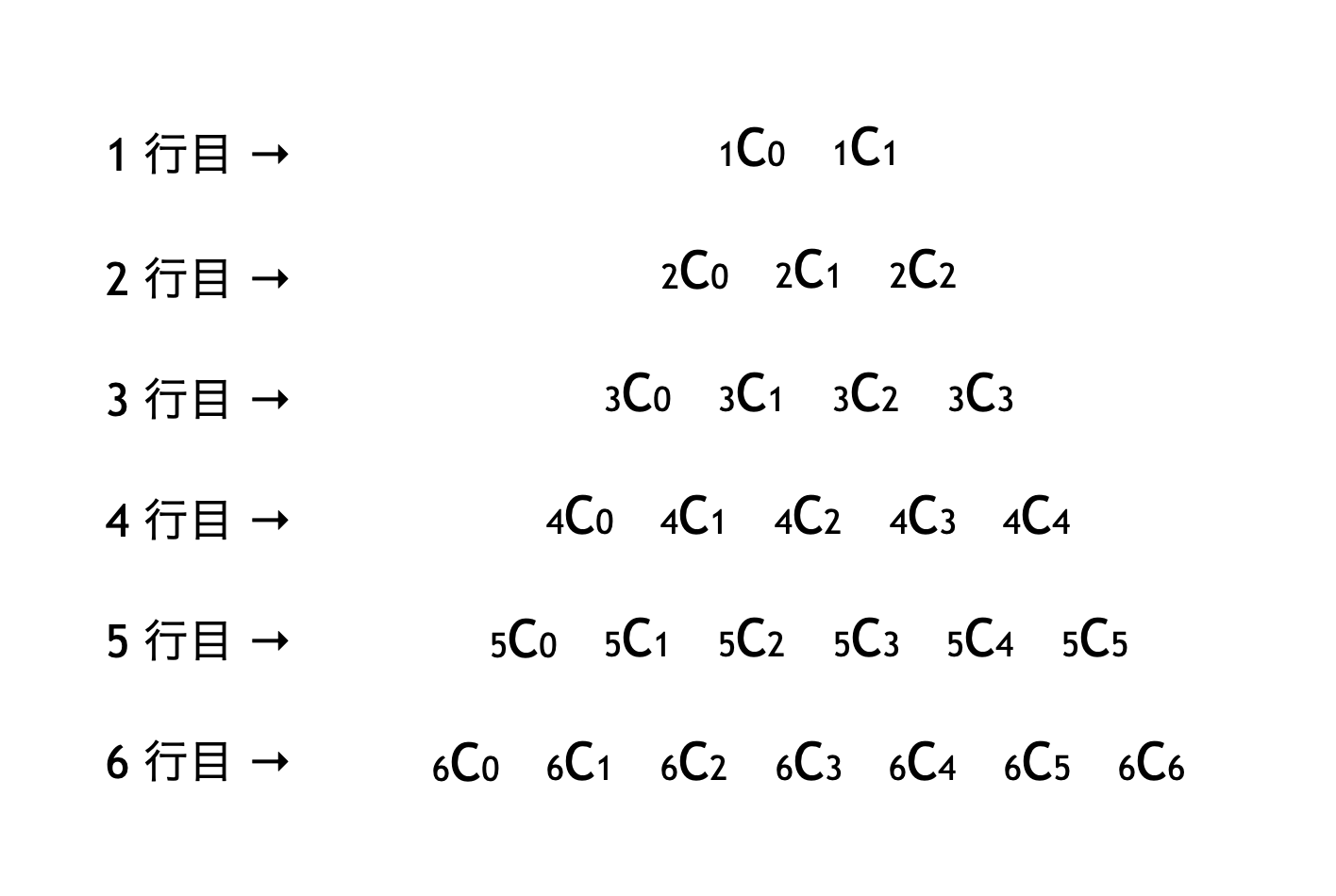
この例題 20 で発見した規則性は、次の等式を表しています。この等式は二項定理によって示せます。
${}_{n}\mathrm{C}_{0} + {}_{n}\mathrm{C}_{1} + {}_{n}\mathrm{C}_{2} + \dots + {}_{n}\mathrm{C}_{n} = 2^{n}$
例題 21： パスカルの三角形 2 (難易度 ★★★☆☆)
パスカルの三角形はさまざまな性質を持ちます。さらに問題を解いてみましょう！
【問題文】
次の図のように、整数が規則的に並んでいます。$100$ 行目の左から $3$ 番目の数はいくつですか。
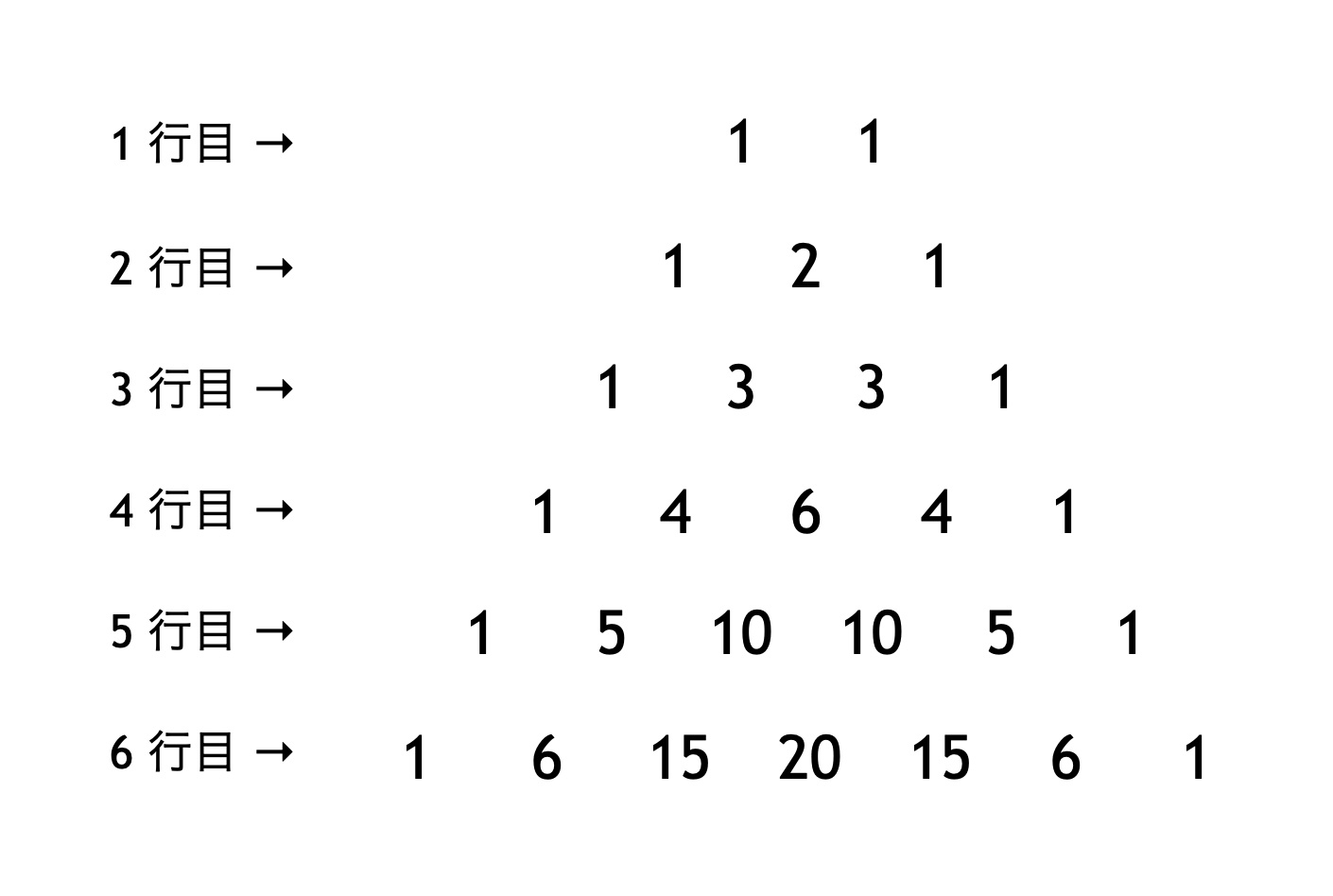
答え
解説
$1, 3, 6, 10, 15, \dots$
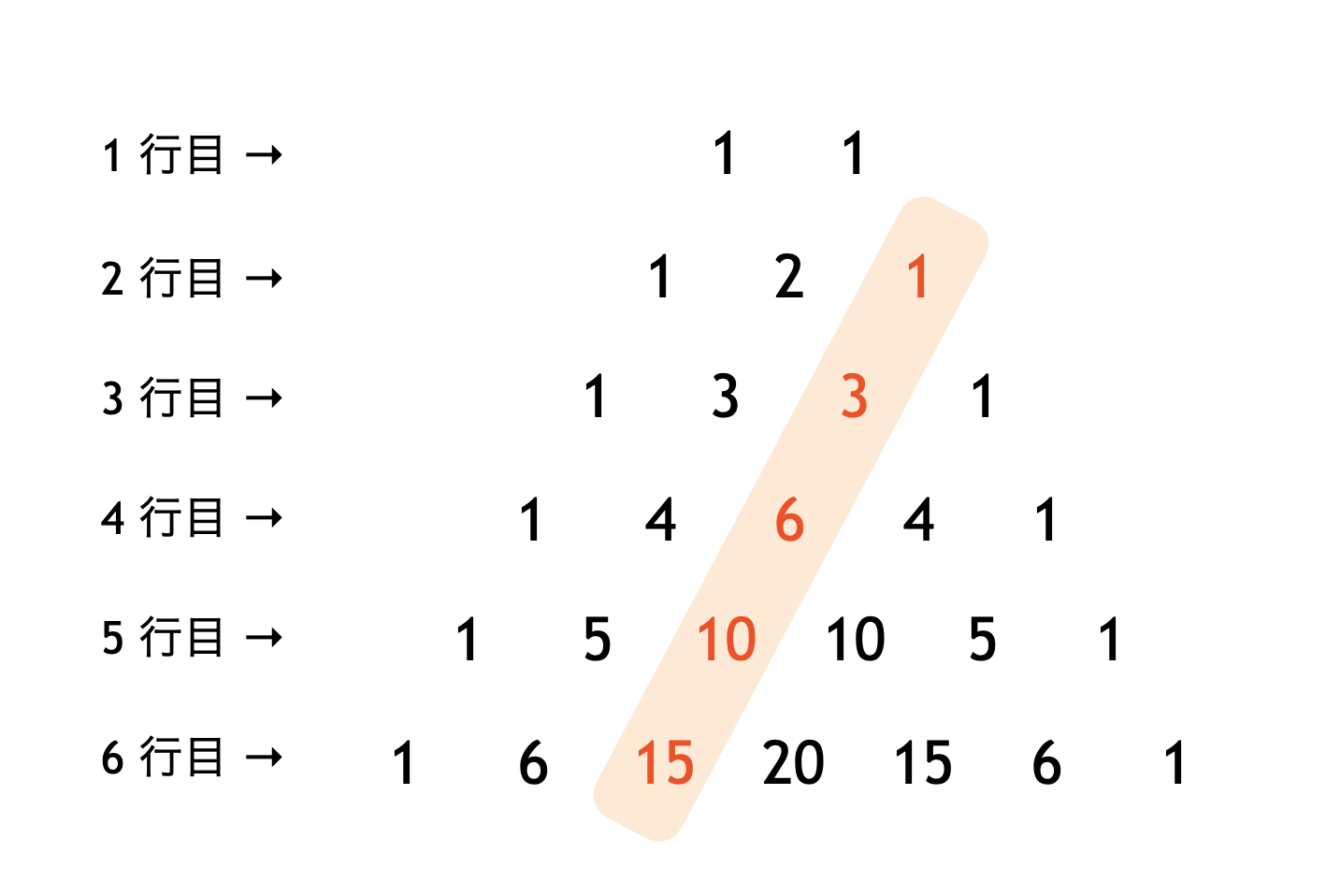
これらの数には、次の法則があります。
- $2$ 行目の $3$ 番目：$1$
- $3$ 行目の $3$ 番目：$3 = 1 + 2$
- $4$ 行目の $3$ 番目：$6 = 1 + 2 + 3$
- $5$ 行目の $3$ 番目：$10 = 1 + 2 + 3 + 4$
- $6$ 行目の $3$ 番目：$15 = 1 + 2 + 3 + 4 + 5$
- $\dots$
よって、$100$ 行目の $3$ 番目の数は、
$1 + 2 + 3 + \dots + 99 = \displaystyle (1 + 99) \times 99 \div 2 = 4950$
と求められます。
「例題 20： パスカルの三角形 1」と同様に、小さい部分について手を動かしてみることで、規則性が見つけやすくなりますね。
なお、この問題で登場した数 $1, 3, 6, 10, 15, 21, \dots$ は三角数とも呼ばれます。次の図のように、三角形の形に並べた碁石の個数を表しています。
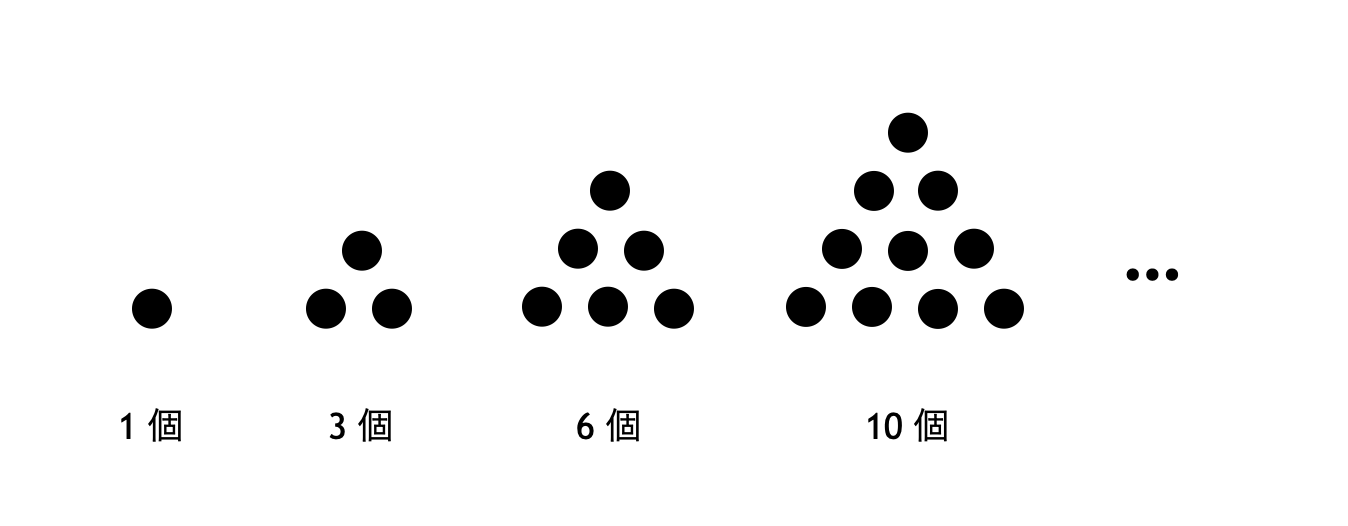
三角数も、中学受験の算数の問題の題材となることがよくあります。
例題 22： Fizz Buzz (難易度 ★★★☆☆)
続いて、ちょっとしたパーティゲーム「Fizz Buzz」を題材とした問題を解きます。
【問題文】
$1$ 以上の整数について、
- $3$ の倍数である数は Fizz
- $5$ の倍数である数は、Buzz
- $3$ の倍数でも $5$ の倍数でもある数は、FizzBuzz
に置き換えて並べます。次のようになります。
$1$, $2$, Fizz, $4$, Buzz, Fizz, $7$, $8$, Fizz, Buzz, ...
$1$ 以上 $1000$ 以下の整数のうち、Fizz、Buzz、FizzBuzz への置き換えをしない数は何個あるでしょうか。
答え
解説
Fizz、Buzz、FizzBuzz への置き換えの様子は、次の表のように周期 $15$ で繰り返されます。
| $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ | $11$ | $12$ | $13$ | $14$ | $15$ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $1$ | $2$ | Fizz | $4$ | Buzz | Fizz | $7$ | $8$ | Fizz | Buzz | $11$ | Fizz | $13$ | $14$ | FizzBuzz |
| $16$ | $17$ | $18$ | $19$ | $20$ | $21$ | $22$ | $23$ | $24$ | $25$ | $26$ | $27$ | $28$ | $29$ | $30$ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $16$ | $17$ | Fizz | $19$ | Buzz | Fizz | $22$ | $23$ | Fizz | Buzz | $26$ | Fizz | $28$ | $29$ | FizzBuzz |
......
この $15$ 個置きの数の塊をブロックと呼ぶことにします。ブロック $1$ 個あたり、数字のまま残る数は $8$ 個ずつあります。ここで、
$1000 \div 15 = 66$ あまり $10$
より、$1000$ 個の数は、$66$ 個のブロックと、$10$ 個の整数から成ります。
- $66$ 個のブロックに含まれる「数字のまま残る数」の個数：$8 \times 66 = 528$ 個
- 残りの $10$ 個の数に含まれる「数字のまま残る数」の個数：$5$ 個
よって、求める個数は
$528 + 5 = 533$ 個
$15$ は $3$ と $5$ の最小公倍数ですね。
一般に、周期 $a$ で繰り返されるものと、周期 $b$ で繰り返されるものが重なっているとき、$a, b$ の最小公倍数を $l$ として、周期 $l$ で同じことが繰り返されることが多々あります。
例題 23： 大宮開成中 2023 年算数 問 5 (難易度 ★★★★☆)
それでは、いよいよ入試問題を解いてみましょう！ このように「操作を繰り返す問題」は頻出ですね。論理的思考力を問うのに格好の題材と言えます。
答え
(1) $15$ 回
(2) $10789$
解説
(1)
実際に操作して確かめてみましょう。
$23$ → $70$ → $35$ → $106$ → $53$ → $160$ → $80$ → $40$ → $20$ → $10$ → $5$ → $16$ → $8$ → $4$ → $2$ → $1$
より、$15$ 回です。
(2)
操作を逆に辿るときは、次の操作をするものと考えてよいです。
- A の逆：$2$ 倍する (偶数でも奇数でも実施してよい)
- B の逆：$1$ を引いて $3$ で割る ($1$ を引いたときに $3$ の倍数になるとき)
よって、「A の逆は常に実施してよい」「B の逆は実施できるときには実施する」というようにして、$2023$ から次の図のように遡れます。求めたいのは「$2$ 番目に大きい数」なので、それよりも小さくなる分岐は省略しています。
図より、答えは $10789$ です。
(2) は操作を逆に辿っていくですね。このような問題は、毎年多くの学校でよく出題されます。コラッツ予想を題材としたものだけでも、
- 駒場東邦中 2023 年算数 問 1(1) (難易度 ★★★★☆)
- 山脇学園中 2022 年算数 問 4 (難易度 ★★★★☆)
- 慶應義塾中等部 2021 年算数 問 5 (難易度 ★★★★☆)
というように、多くの出題例があります。さらに、コラッツ予想とは操作を少し変えた問題 (奇数は単に $1$ を足すなど) も含めると、本当に多いです。その中でも、次の問題はとてもおすすめです！
- 灘中 (2 日目) 2023 年算数 問 1 (難易度 ★★★★☆)
- 栄光学園中 2023 年算数 問 3 (難易度 ★★★★★)
ぜひ解いてみてください！
6 章： 最難関校の入試問題
それでは、いよいよ最難関校の入試問題に挑戦してみましょう！
例題 24： 開成中 2018 年算数 問 3 (難易度 ★★★★★)
中学受験の算数には、その時その時の流行があるように思います。たとえば、近年は「連続する整数の和」がよく出題されているように思います。次の問題は、そのブームの先駆けとなったものです。
答え
(1) $4$-$10$
(2) $18$-$22$, $9$-$16$
(3) $8$ 通り | $3, 5, 8, 9, 15, 24, 25, 40$ 種類
解説
全体を通して、「連続する整数の和」がある数になるように、連続する整数を求めるという問題です。
(1)
正方形に登場する整数の最小値を $x$ とし、登場する整数の種類数を $l$ とします。このとき、$x$ から $x + l - 1$ までの整数の和が $7 \times 7 = 49$ となればよいです。よって、
$(x \times 2 + l - 1) \times l \div 2 = 49$
と表せます。これより、
$(x \times 2 + l - 1) \times l = 98$
となります。これより、$l$ は $98$ の約数となります。また、$x \times 2 - 1$ は $1$ 以上なので、$l$ は $(x \times 2 + l - 1)$ より小さいことが分かります。また、正方形内に $3$ 種類以上の整数が必要であることから、$l$ は $3$ 以上でなければなりません。
これらの条件を加味すると、$l = 7$ に絞られます。このとき、$x \times 2 + 7 - 1 = 14$ より、$x = 4$ です。以上より、$4$ から $10$ までの整数を並べればよいです。
(2)
(1) と同様に、正方形に登場する整数の最小値を $x$ とし、登場する整数の種類数を $l$ とすると、
$(x \times 2 + l - 1) \times l = 200$
となります。よって、$l$ は $200$ の約数です。ここで、次のことに注意しましょう。
- $l$ が偶数ならば $x \times 2 + l - 1$ は奇数である
- $l$ が奇数ならば $x \times 2 + l - 1$ は偶数である
この性質を利用すると、$l$ の値を絞りやすくなります。
- $l = 4, 10$ のとき、$l$ と $x \times 2 + l - 1$ がともに偶数になるので適さない
- $l = 5$ のとき、$x \times 2 + 5 - 1 = 40$ より、$x = 18$ である
- $l = 8$ のとき、$x \times 2 + 8 - 1 = 25$ より、$x = 9$ である
よって、「$18$ から $22$ までの整数」または「$9$ から $16$ までの整数」を並べればよいです。
(3)
(1) と同様に、正方形に登場する整数の最小値を $x$ とし、登場する整数の種類数を $l$ とすると、
$(x \times 2 + l - 1) \times l = 1800$
となります。よって、$l$ は $1800$ の約数です。先ほどと同様に、
- $l$ は $3$ 以上である
- $l$ は $x \times 2 + l - 1$ より小さい
- $l$ と $x \times 2 + l - 1$ は一方が偶数であり、他方が奇数である
という条件を満たすものを求めます。
- $l = 3$ のとき、$x \times 2 + 3 - 1 = 600$ より、適する
- $l = 5$ のとき、$x \times 2 + 5 - 1 = 360$ より、適する
- $l = 8$ のとき、$x \times 2 + 8 - 1 = 225$ より、適する
- $l = 9$ のとき、$x \times 2 + 9 - 1 = 200$ より、適する
- $l = 15$ のとき、$x \times 2 + 15 - 1 = 120$ より、適する
- $l = 24$ のとき、$x \times 2 + 24 - 1 = 75$ より、適する
- $l = 25$ のとき、$x \times 2 + 25 - 1 = 72$ より、適する
- $l = 40$ のとき、$x \times 2 + 40 - 1 = 45$ より、適する
よって、正方形に並べる整数の種類数は、$3, 5, 8, 9, 15, 24, 25, 40$ の $8$ 通りです。
「連続する整数の和」を扱う問題は、最近は毎年のように出題されています！
- 渋谷教育学園幕張中 2020 年 問 2 (難易度 ★★★★★)
- サレジオ学院中 2021 年 問 4 (難易度 ★★★★★)
- 筑波大学附属駒場中 2022 年 問 1 (難易度 ★★★★★)
- 駒場東邦中 2023 年 問 3 (難易度 ★★★★★)
これらはいずれも、「奇数の約数を考える」ことがポイントとなります。
例題 25： 灘中 (2 日目）2021 年算数 問 2 (難易度 ★★★★★)
もう 1 問、とても面白い入試問題を解いてみましょう！
答え
(1) $37$
(2) $175$
(3) $781$
解説
(1)
マス目の数値の偶数・奇数のみが大事であることに注意します。
- 奇数と奇数の和と、偶数と偶数の和は偶数
- 奇数と偶数の和は奇数
であることを利用して、奇数を「×」、偶数を「⚪︎」で表記すると、下図のようになります。
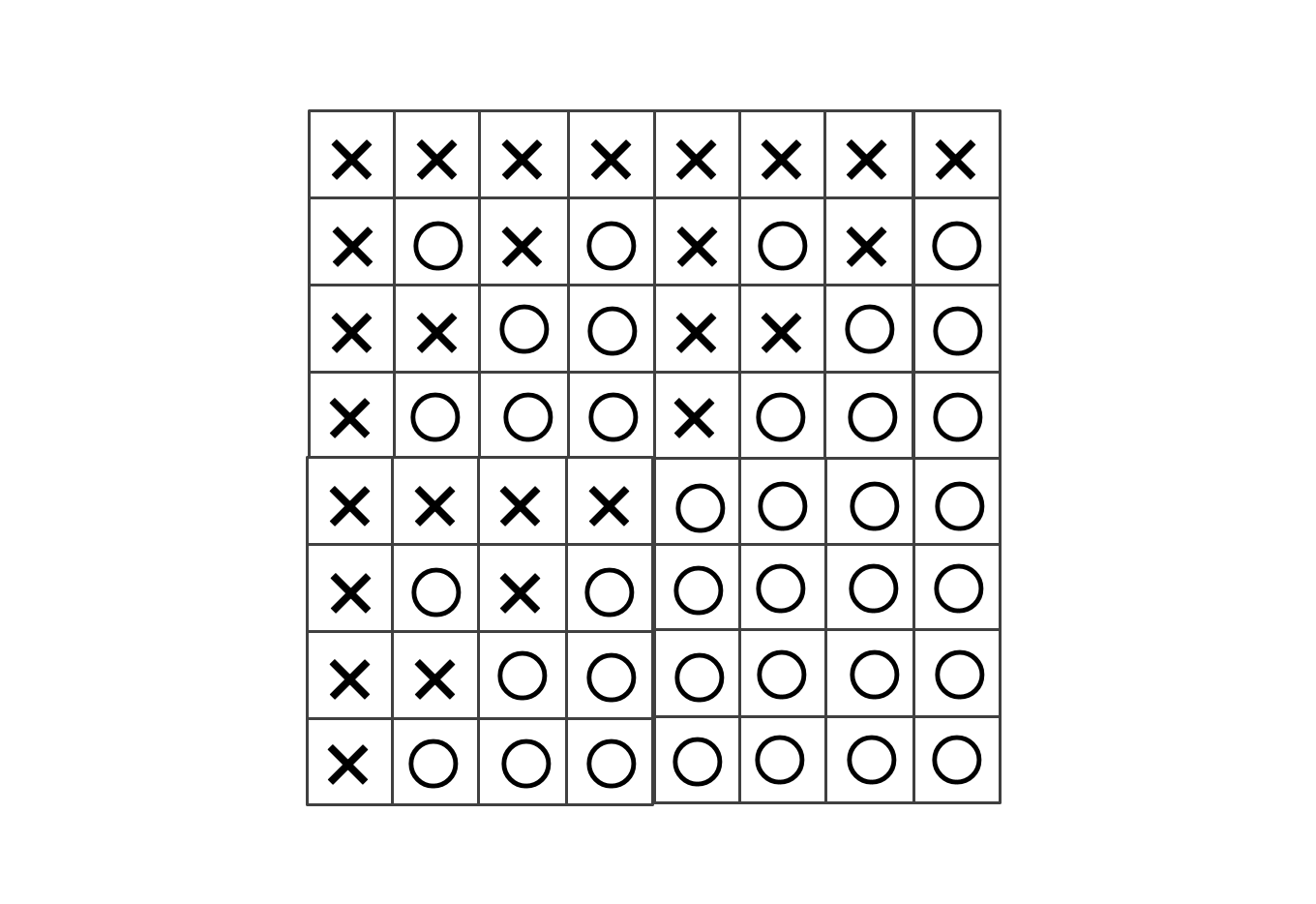
よって、「⚪︎」のマス数を数えて、$37$ 個と求められます。
(2)
$8 \times 8$ の「×」「⚪︎」の模様は、下図のように
- 左上・右上・左下の $4 \times 4$ は同じ模様である
- 右下の $4 \times 4$ はすべて「⚪︎」である
というようになっています。
同様のことは、$16 \times 16$ でも成り立つと考えられます。つまり、
- 左上・右上・左下の $8 \times 8$ は、それぞれ $37$ 個の「⚪︎」がある
- 右下の $8 \times 8$ は、すべて「⚪︎」であって、$64$ 個の「⚪︎」がある
というようになっています。
よって、「⚪︎」のマスの個数は $37 \times 3 + 64 = 175$ 個と求められます。
(3)
$32 \times 32$ についても、同様に、
- 左上・右上・左下の $16 \times 16$ は、それぞれ $175$ 個の「⚪︎」がある
- 右下の $16 \times 16$ は、すべて「⚪︎」であって、$256$ 個の「⚪︎」がある
というようになっていると考えられます。
よって、「⚪︎」のマスの個数は $175 \times 3 + 256 = 781$ 個と求められます。
7 章： 中学受験算数の攻略ポイント
ここでは、実際に中学受験を目指す方々に向けて、偏差値別の攻略ポイントを書いていきます。なお、ここでいう偏差値は、四谷大塚の合格確率 80% 判定の偏差値のことを指すものとします。
偏差値 30 台の方へ
もしかしたら、算数に苦手意識があるかもしれないですね。でも大丈夫！ 算数は確かに天才的な思考力が必要な問題もあるのですが、偏差値 $55$ までは、基本問題が完璧に解ければ到達できるのです。 まずは、計算力を徹底的に鍛えましょう！
たとえば、次のような計算を確実にこなせるでしょうか。$□$ にあてはまる数を求めてみましょう。
(1) $99 \times 87 + 113 \times 99 = □$
(2) $3700 \mathrm{m}^{2} = □ \mathrm{km}^{2}$
(3) $\displaystyle 9.7 - \frac{5}{12} \div (□ + 1\frac{1}{3}) \times 3.8 = 8.7$
計算問題の答え
(1) $19800$
(2) $0.0037$
(3) $\displaystyle \frac{1}{4}$
このような計算問題に対して、自信をもって取り組めるようになることが大切です。算数で躓く原因は計算力にあるというケースはとても多いです。つるかめ算のような文章題に取り組む際にも、計算力があるのとないのとでは、習得しやすさに差が生まれます。数や規則性などの分野でも、計算力があれば数の感覚を磨きやすいです。
計算力を鍛えるためには、とにかく毎日計算に触れることが大切です。一例として、
- 四谷大塚： 『予習シリーズ 計算』 シリーズ
- 桜井信一, 馬渕教室： 『中学受験テキスト 下剋上算数』
といった教材を 1 つ決めて、毎日やり込みましょう。計算がスラスラできるようになれば、驚くほど算数がわかるようになってくるはずです！
偏差値 40 台の方へ
忘れられがちなことなのですが、四谷大塚基準で偏差値 $40$ を取れるような児童は、学校のクラスではとても勉強ができる側にいるはずです！ 学校の算数のテストではいつも満点近くをとることができるのに、合否判定テスト (四谷大塚) のような中学受験の模試では半分も解けない......そんな苦しみを抱えているかもしれません。
まずは、自信を持ちましょう。そして、問題を解いたときにミスに気付けるようになることを目指しましょう。偏差値 $40$ 台の生徒さんが模試を受けたときによくあることとして、「あとで落ち着いて問題を解いてみると、この問題も解けたし、あの問題も解けた......」となることがあります13。計算ミスさえしなければ、偏差値 $50$ は十分に狙えるはずなのです。
計算ミスを防ぐためには、「自分が何を求めたのか」を意識することが大切です。たとえば、次の問題を考えてみましょう。
自動車が同じスピードで、$30$ km 離れた場所へ、$30$ 分かけて到着しました。自動車は時速何 km で走っていたでしょうか。
「速さ = 距離 ÷ 時間」に当てはめて、何も考えずに $30 \div 30 = 1$ [km / h] と答えてしまった方もいるかもしれません。しかし、自動車の速度が時速 $1$ km などという答えは現実的でしょうか。人が歩くのでも時速 $4$ km 程度なので、明らかにおかしいですね。正しくは、$30$ 分は $0.5$ 時間なので、$30 \div 0.5 = 60$ [km / h] となります。
このように、間違った答えに対して「明らかにおかしいな......」と思える勘を磨くことがとても大切です。そのような勘が育てば、テストの点数も大きく上がるでしょう！
もう 1 つの大切なポイントは比の感覚を磨き上げることです。偏差値が 40 台の生徒さんを見ていると、比の感覚が十分に育っていないと感じることがよくあります。比は、文章題だけでなく、「速さ」「濃度」「平均算」「損益算」「平面図形」など、算数のあらゆる場面で活躍します。さらに、算数だけではなく、理科でも大活躍します。比の練習をたくさんしていきましょう。比を制する者は中受を制するといっても過言ではないでしょう！
偏差値 50 台の方へ
中学受験の算数では、偏差値 $55$ 付近に大きな壁があると言われています。偏差値 $55$ までであれば、基本問題をミスなく完璧にこなせれば到達できます。しかし、偏差値 $55$ から先へ進むためには、より高度な論理的思考力を要する問題が解けるようになる必要があるのです14。
しかし、やはり一歩一歩着実に階段を上がっていく他はありません。まずは、基礎をしっかりと盤石なものにしましょう。一例として、四谷大塚の『予習シリーズ』シリーズの問題を確実に解けるようにしておきましょう (他の参考書でもよいです)。
ここで、ひとつ注意しておきたいことは、「無闇に多くの参考書に手を出す必要はない」ということです。算数という科目には、ある参考書の問題をちゃんと理解して解けるようにすると、他の参考書の問題も自然に解けるようになる傾向がある、という特徴があります。逆に、1 つの参考書を完璧にできたと思ったら、そのときはぜひ、他の参考書の問題も解いてみてください。きっと、結構解けるようになっているはずです！
基礎が盤石になると、徐々に上の世界が見えて来るようになります。たとえば、基礎を 2 つ組み合わせれば解けるような問題が解けるようになります。できれば、6 年生の夏までにこの状態に到達したいところです。6 年生の夏までに基礎が固まっていれば、塾の夏期講習などで、難関校対策のコースに入り込めるはずです15。難関校対策のコースに入ることができれば、夏休み期間中にひたすら塾に通うだけでも、難しい問題にたくさん触れることができます。夏休み期間中は、塾から提供される問題をこなすだけでほとんどの時間を費やすような生活になるはずです。それでよいと思います。
そんな生活を繰り返していると、6 年生の秋頃には、いつの間にか難関校の問題が結構解けるようになっていることに気づくと思います。そうしたら、今度は過去問演習に取り組んでいきましょう！
偏差値 60 台の方へ
このレベルになると、そもそも該当する学校の数が絞られてきます。ですので、6 年生になる頃には、志望校がいくつか決まっているという生徒さんも多いでしょう。そこで、志望校に合わせたトレーニングが重要な意味を持ち始めます。早い段階で過去問演習をする必要はないのですが、志望校の過去問の傾向を早めに掴んでおくとよいでしょう。
同じ偏差値帯であっても、基本問題が中心でミスなく完璧にこなせることを重視する学校もあれば、難しい問題が中心でより多くの問題が解けることを重視する学校もあります。答えだけを書く問題を中心に出題する学校もあれば、すべての問題で記述をしっかり書かせる学校もあります。志望校の問題を解くために必要な能力を把握しておくことで、自分に足りない能力を意識することができ、日々のトレーニングを効率化できます。
また、このレベルであっても日々の計算練習だけは怠らないようにしましょう。計算力を鍛えれば、数の感覚が研ぎ澄まされていきます。そうすると、次のような効果があります。
- 整数の応用問題で、重要な気づきが得られやすくなる
- 暗算で解ける問題の幅が広がり、練習の効率化に繋がる
- 「この問題はなぜこの数値に設定されたのか」という出題者の意図の部分が読み取れるようになり、自分の答えが合っているという確信が得られやすくなる
偏差値 70 台の方へ
全国模試でベスト $100$ 位以内に入れるような高順位を何度も取っていると思います。このレベルだと、勉強自体が楽しくて、模試はゲーム感覚で楽しんでいる方も多いでしょう。そんな中でも、もし算数が特に好きでしたら、算数オリンピックなどに挑戦してみるのも面白いと思います！ 本物の天才パズルの世界が君を待っています！
8 章： 中学受験の光と影
ここまで「中学受験の算数」の世界を紹介してきましたが、中学受験そのものについても簡単に触れておきたいと思います。中学受験に対しては、各自がさまざまな思いを抱えていると思います。小学生のときに親の期待を背負いながら週 4〜5 回もの塾通いに苦しんだ者もいれば、反対に模試という全国対戦ゲームを楽しんだ者もいます。また、地方出身の方々など、そもそも周囲に中学受験に関する情報がなく、大人になってから中学受験のことを知ったという人もいます。もっと早くから知りたかったという思いを抱える人も少なくないでしょう。
中学受験に関する話題は、賛否両論の嵐が吹き荒れることも珍しくありません。人によって、歩んできた人生が大きく異なるためでもあります。中学受験の是非を論じるためには、多くの側面から考える必要があるでしょう。今回は、それらすべてを紹介することは到底できませんが、一端を綴ります。なお、個人的な経験に基づく話も多いことをあらかじめお断りしておきます。
8-1： 中学受験のメリット (学力面)
まず、純粋な学力面 (特に数学) について考えてみましょう。学校側から見たときに、中学受験を突破した生徒を中高一貫で指導できるメリットとしては
- 中学生のうちから数学 IA の指導に入れること
- 生徒が入学時点で、すでに数学 IA に含まれる要素の半分近くを学んでいる状態であること
が挙げられます。高校数学は中学数学の 3 倍程度の分量があるため、大学受験を目標と考えたときに、中学数学の習得に 3 年、高校数学の習得に 3 年をかけるのはバランスが悪いといえます。特に、難関大学を目指す上では、数学 IIIC をいかに早い段階で完成させられるかが鍵を握ります。実は、大学受験の数学の問題で難しいのは数学 IA であり、同じ単元をレベルアップしながらスパイラル学習していく戦略が有効ですが、数学 IIIC を終わらせるのに精一杯だと、その余裕がありません。
中学受験をすることで、多くの場合には、高校受験をスキップすることができます。そのおかげで、早い段階から高校数学を学ぶことができます。
8-2： 中学受験のメリット (環境構築面)
中学受験には、学力面だけでなく、中高生時代を過ごす環境を構築する面においてもメリットがあります (同時にデメリットもあります)。
公立中学は、その性質上、たまたま同時期に近くの地域で生まれたメンバーがクラスメートとなります。家庭環境や価値観などが大きく異なる生徒同士が、お互いに居心地の悪さを感じるというケースも少なくないでしょう。それに対して、中学受験をする場合は、自分が中高生活を送る環境をある程度決めることができます。学校ごとに個性があり、似た家庭環境で育ち、似た価値観を持つ人が集まりやすい傾向にあります。
8-3： 中学受験のデメリット (家庭環境面)
中学受験は、必ずしもいいことばかりとは限りません。中学受験の重圧によって、とても苦しい思いをしている子どもも多いのが実情です。たとえば、
- 親の期待が重たく、プレッシャーが苦しい
- テストがあるたびに、その点数が悪いことで親に怒られることが怖い
- 遊びたい盛りに、週 4〜5 日も塾通いをすることが辛い
- 小学校で仲のいい友達と離れ離れになってしまうことが寂しい
- 中学受験をするということについて、小学校でネガティブな目で見られてしまう
- 厳しい受験競争に晒されて、神経をすり減らしてしまう
などという現実があります。子どものパーソナリティや能力などを多角的に把握して、その子どもにとって本当に中学受験が幸せなものなのか、熟考することが求められると言えるでしょう16。
8-4： 中学受験の影 (社会的側面)
ここまで、中学受験のメリット・デメリットを「個人」について考えましたが、社会全体について考えることも必要でしょう。よく聞くのは
- 中学受験をするのは首都圏の子どもたちに偏っていて、地方ではそもそも中学受験をするという選択肢が認識されていない
- 仮に中学受験をするという選択肢が認識されていたとしても、自宅から通学可能な範囲内に、中学受験をするような学校がない
という悩みです。中学受験に対しては、地域ごとの教育格差を拡大しているものだというイメージを抱いている方も少なくないでしょう。
個人的な思いとしては、中学受験をすることで人生が良い方向に変わっていくタイプの子どもたちに対しては、住む地域によらず、中学受験の恩恵を受けられるようになったらよいと考えています。この問題は非常に難しく、社会全体で考えていく必要のある課題だと思います。
9 章： 本記事の先へ
本記事では、中学受験の算数で出題される分野を多くを解説してきました。しかしながら、まだまだ紹介しきれていない問題がたくさんあります。本記事を通して中学受験に関心を抱いた方へ向けて、さらに詳細を知りたい方のためのガイドを示します。
9-1： 本記事で扱えなかった分野
本記事で十分に扱えなかった分野を下の表に挙げます。これらの分野を扱えなかったことは心残りです。ぜひ、下の参考書籍などで補ってみてください。特に、「場合の数」については、また別途記事にしたいと思います。
| 大分野 | ポイント |
|---|---|
| 速さ | 速さは「比」の概念の応用といえます |
| 数の性質 | 最大公約数や素因数分解といった、整数の性質に関する問題もよく出題されます |
| 場合の数 | 何通りかを数える問題も定番ですね！ |
| 平面図形と比 | 平面図形において、面積比を求める問題など、比が絡む問題もよく出題されます |
| 立体図形 | 高度な空間認識能力が求められる問題も多いです |
9-2： 参考書籍
中学受験に向けて、参考になる書籍を挙げていきます。
書籍(1) 受験研究社： 『小学高学年 自由自在』
学校の算数の話から、中学受験にまで使える話まで、一冊にコンパクトにまとまっています。オールカラーで、ページを眺めるだけでも図鑑のように楽しめるのも魅力的です。説明も、とても分かりやすいです。大人の方に対しても、中学受験の算数の世界を知るための最初の一冊としてオススメです！
書籍(2) おおたとしまさ： 『勇者たちの中学受験~わが子が本気になったとき、私の目が覚めたとき』
中学受験というと、「どうやって成績が上がるか」に意識が集中しがちかもしれません。しかし、それと同じくらい大切なのは、親と子どもがいかに一緒に走っていくかだと思います。よく、中学受験は親子の二人三脚だとも言われますね。この本は、子どもとの向き合い方について、さまざまな気づきを与えてくれます。
書籍(3) 四谷大塚： 『予習シリーズ』 シリーズ
中学受験対策本としてお馴染みの『予習シリーズ』です。各科目について、4 年上、4 年下、5 年上、5 年下、6 年上、6 年下 (有名校対策と難関校対策) というように、学年別にまとまっています。理論上はこのシリーズのみで中学受験に挑戦できる程度に、中学受験に必要な知見がまとまっています。
書籍(4) 四谷大塚： 『予習シリーズ 計算』 シリーズ
予習シリーズには、計算力を集中的にトレーニングできる『予習シリーズ 計算』もあります。こちらもオススメです！
書籍(5) 桜井信一, 馬渕教室： 『中学受験テキスト 下剋上算数』
$1$ 日 $10$ 分で $10$ 問ずつ、$100$ 日間解いていくことで、$1000$ 問もの演習を積み上がるという本です！ ジリジリと難易度が上がっていく構成になっているので、気がついたら大きくレベルアップできるのが魅力的です。基礎編と難関校受験編があります。
書籍(6) 安浪京子, 富田佐織： 『カリスマ家庭教師が秘策を伝授! 中学受験「算数」教え方のコツ』
中学受験を志す子どもにどう教えたらいいか悩む親御さんも多いでしょう。この本は、そんな親御さんの悩みに向き合う本です。子どもが躓きやすいポイントを網羅していて、その対策方法をしっかりと解説してくれています。
書籍(7) 学参東京出版： 『中学への算数』 (月刊誌)
算数が大好きなら、東京出版が毎月発刊する『中学への算数』もオススメです！
- レベルアップ演習：上位 $3$ 割の中学を目指す人向け (難易度 ★☆☆☆☆〜★★☆☆☆ 相当)
- 日々の演習：上位 $1$ 割の中学を目指す人向け (難易度 ★★★☆☆〜★★★★☆ 相当)
- 発展演習：算数が得意な小学生向け (難易度 ★★★★★ 相当)
というように、読者のレベルに応じたコンテンツが用意されています。さらに、「算数の周辺」や「科学のお話」など、好奇心をくすぐるような特集記事もあります。
書籍(8) 難波博之： 『学校では絶対に教えてもらえない超ディープな算数の教科書』
この本は中学受験向けというよりは、これから中学校に入学する人が読むと学びが多そうです。題材は算数ですが、「定義を大切にすること」など、数学を学ぶ上での大切な考え方を説いています。大人になってから、算数や数学を学び直したい方にも最適でしょう。
書籍(9) ソニー・グローバルエデュケーション： 『５分で論理的思考力ドリル』
ソニー・グローバルエデュケーションは、論理的思考力というものを、$5$ つの思考回路「スキャン」「クリエイト」「リバース」「ノック」「ステップ」に分解して捉えました。これらの思考回路は、中学受験の算数の問題を解く際にも重要な役割を果たします。頭の体操として挑むのも楽しい本です。
書籍(10) 算数オリンピック委員会： 『算数オリンピックに挑戦』
中学受験の算数のみでは飽き足らない算数好きのための、ワクワクするような大会があります。それが、算数オリンピックです。過去問を集めた本も出版されているので、ぜひ挑戦してみてください！
-
文部科学省の資料では、小学校段階におけるプログラミング教育については、コーディング （プログラミング言語を用いた記述方法） を覚えることがプログラミング教育の目的であるとの誤解が広がりつつあることが、プログラミング教育が必要な理由の 1 つであるとしています。 ↩
-
この練習法における「中学受験レベルの算数能力」と、本記事で紹介する「中学受験の算数」とでは、想定レベルに乖離がある可能性が高いことには注意が必要です。しかしながら、中学受験の算数に触れることは、世界を目指すレベルに限らず、あらゆるレベル帯の競技プログラマにとって有益だと思います。 ↩
-
中学受験や大学受験において、学校・大学の偏差値とは、その学習塾におけるその偏差値の生徒が 80% の確率で合格できると想定されるような数値を表すことが多いです。また、大学受験の模試においては、80% の確率で合格できるだろうという判定は A 判定などとも呼ばれます。 ↩
-
明らかに難易度がおかしいと感じる問題がありましたら、気軽に意見を寄せていただければと思います。また、AtCoder に取り組んでいる方向けの補足として、茶色を目指すためには、★★★☆☆ までの素養があると有利だと思います。緑色を目指すためには、★★★★☆ までの素養と、一部の ★★★★★ の素養があると有利だと思います。 ↩
-
また、より一般に「ご石を並べたものを異なる並べ方で再配列する」という設定の問題もよく見られます。方陣算などとも呼ばれるものですね。 ↩
-
AtCoder においても、このテーマの類題が数多くあります。ぜひ、ABC 153 A - Serval vs Monster、ABC 173 A - Payment、ABC 192 A - Star、ABC 176 A - Takoyaki、ABC 139 B - Power Socket なども解いてみてください。 ↩
-
情報科学では、スタートの番号を $0$ にする方が一般的です。その場合、$n$ 個目の番号は $n-1$ と表されます。この $n-1$ という値が植木算そのものを表しているともいえます。 ↩
-
AtCoder でも、関連問題は多く出題されています。たとえば、ぜひ ABC 318 A - Full Moon や ABC 334 B - Christmas Trees などを解いてみてください！ ↩
-
ソニー・グローバルエデュケーションが論理的思考回路の 1 つとして提唱する「スキャン回路」は、図形問題では大活躍します。 ↩
-
AtCoder でも、ARC 104 A - Plus Minus など、和差算を題材とした問題が出題されています。ぜひ挑戦してみてください！ ↩
-
この問題は、ほぼそのままの問題が過去に AtCoder でも出題されています。ぜひ、ABC 183 B - Billiards を解いてみてください！ ↩
-
そもそも、模試を受けたあとに復習をしていない場合は、ぜひ復習をちゃんとやりましょう。本来解けたはずの問題を洗い出して、次からは解けるようになるための対策を考えることが大切です。 ↩
-
論理的思考の壁を偏差値 60 だと主張する人もいます。基本問題を早く正確に解ける人ならば、確かに偏差値 60 まで到達できる可能性はあると思います。いずれにしても、受験対策としては「基礎を盤石にする」という方針に変わりないですね。 ↩
-
塾によって体制は異なると思われます。塾に難関校対策のコースがないか、塾には通わずに自学している場合なども考えられます。その場合であっても、難関校の問題に自然に触れられるような環境を構築することが大切です。 ↩
-
たとえば、神経症傾向の大きな子どもにとっては、順位のつく競争に対してネガティブな感情を抱きやすいという研究報告もあります。 ↩