まずは挑戦してみよう
シェーダを自分でコーディングするなんて……
きっとお難しいんでしょ……
と、お思いの奥様方。そんなことはないんです。コツをつかめば意外と楽しめます。当連載では、シェーダというものに対して抱かれてしまいがちな、漠然とした 難しそう感 を払拭すべく、簡単なシェーダの記述とその基本について解説したいと思います。
前回:[連載]やってみれば超簡単! WebGL と GLSL で始める、はじめてのシェーダコーディング(3) - Qiita
想定する読者
当連載では、シェーダってなんか難しそう……とか、シェーダプログラミング始めてみたいけど……とか、なんとなく興味を持ってるけどシェーダを記述したことがない方を読者に想定しています。
たとえば Unity などのツール、あるいはマインクラフトのようなゲーム、またはモデリングソフトなどでもシェーダを自分で記述することができるような世の中です。きっとシェーダに触れた経験は無駄にはならないでしょう。
すぐに業務で活かすとか、そういう壮大な話はさておいてまずは気軽にシェーダに触れてみましょう。
難しい 3D の数学的知識はとりあえず要りません。もちろん難しいことをやろうとする場合は話が変わってきますが、当連載ではそのあたりの知識は求めません。ちょっとくらい、三角関数とかは出てきますがそんなに難しくないですから安心してください。
対象のシェーダ記述言語は GLSL
「シェーダ」という言葉には非常に広い意味が含まれるので、世の中にはシェーダといってもいろいろなものが存在しています。また、それを記述するための専用の言語にも、いくつか種類があったりして非常に初心者には敷居が高いのかなと思います。
当連載では GLSL というシェーダ専用言語を用います。
GLSL は 昨今話題の WebGL でも採用されているので、特別な開発環境の準備などをしなくても、ブラウザとテキストエディタさえあれば簡単に始められます。
また、当連載では著者自作の GLSL editor というオンラインでシェーダが記述できるエディタを使いますので、もはやブラウザとネット環境さえあればシェーダが書けます。気軽ですね。
それでは早速、前回に引き続き、シェーダプログラミングについて考えていきましょう。
見栄えのする描画結果を得るには
前回は時間の経過によってアニメーションするような、動的なシェーダの記述について解説しました。
今回は、前回の内容も踏まえつつ、もう少し模様に見えるようなものを画面に描き出すことに挑戦してみましょう。
比較的簡単に、しかも割と見栄えのする映像を作り出すポイントは、ずばり 光っぽい表現を入れる ことじゃないかなあと個人的には思います。幻想的な、何とも言えない光の表現には反射的に目を奪われるものです。
今回は最終的に光輝くオーブ(光の玉)を画面にレンダリングすることを目標に、ひとつやってみることにしましょう。
シェーダ内の座標を正規化する
さて、光のオーブを描く前に、事前の準備としてまずはシェーダ内の座標を扱いやすいように正規化することから始めてみましょう。
むむっ! 正規化なんて難しいことはわからないぞ!
と思った方もいるかもしれませんが、正規化と難しい言葉を使ってしまうとややこしい印象かもしれませんが、要は簡単に言うと、この場合 値を扱いやすいように調整すること を指しています。
思い返してみてほしいのですが、当連載でも既に登場している gl_FragCoord という GLSL の組み込み変数がありましたよね。これは、これから処理しようとしているピクセルの座標があらかじめ格納されている特殊な変数でした。
この組み込み変数を用いれば、処理対象のピクセルの座標を計算に用いることができるようになり、その結果スクリーン上の位置によって異なる色の出力ができるようになるわけですが……正直、そのまま gl_FragCoord の値を使うのは少々面倒です。
というのも、0 ~ 512 のような、非常に範囲の大きな数値を使ってしまうと計算がイメージしにくくなります。0 ~ 512 の範囲の 80% っていくつ? みたいに聞かれると、一瞬考えてしまいますよね。もしこれが、0 ~ 1 の範囲の中の 80% は? だったとしたら、即座に 0.8 という数値が出てくると思います。
このように、人間が数字を考える上でも、また 3D を含む座標系を考える意味でも、値が一定の範囲内に収まっていたほうがなにかと都合がいい場合が多いのですね。
正規化とは、この一定の範囲内に値が収まっている状態になるように、数値を調整することを言うんですね。
正規化のためのコード
さて、それでは具体的にどのようなコードを記述すれば、上手に正規化が行えるのでしょうか。
先に言っておくと、正規化する方法はいろいろ考えられますのでこう書かないと動かないよ! といった厳密な答えがあるわけではありません。
当連載では、座標の正規化を次のようなコードで実現します。
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y); // r は resolution
ちょっと横に長ったらしいですが、落ち着いて考えていきましょう。
何度も書いているように、GLSL editor ではスクリーンのサイズが、縦横いずれも 512px です。つまり gl_FragCoord の X と Y 要素にはそれぞれ 0 ~ 512 の範囲の値が、その処理されようとしているピクセル位置によって格納されていることになります。
そして、外部からデータが送られてくる uniform 変数である r には、スクリーンの大きさ、つまり 512 があらかじめ格納されています。
それを踏まえてよくよくコードを見てみましょう。
まず最初の左側の括弧のなかでは gl_FragCoord の値を二倍してから変数 r を減算していますね。つまり 0 ~ 512 の範囲を持つ gl_FragCoord が、二倍されたことによって 0 ~ 1024 となり、そこから resolution の 512 が引かれるわけです。
これによってまず、括弧の中身の値は -512 ~ 512 の範囲に変換されるのがわかりますね。
続けて、その変換済みの値を resolution で除算しています。resolution、つまり変数 r の中身は先ほども書いたように GLSL editor では 512 です。となると、先ほどの変換済み数値を 512 で割ることになるので、値はさらに変換されて -1 ~ 1 の範囲に整形されることになります。
これで、晴れて正規化は完了です。
簡単ですね。
正規化が済んだことによって、今までは……
- 左下を原点として 0 ~ 512 までの範囲を持つ座標
だったものが、スクリーンの中央が原点となり、上下左右には -1 ~ 1 の範囲を持つ座標系になるわけですね。座標が正規化されている状態であれば、計算がいろいろとやりやすくなるだけでなく、頭の中で数字をイメージする際にも非常にわかりやすくなります。
補足コラム
先ほどの正規化のコードでは、除算する値にmin関数を使っています。これはどうしてかというと、スクリーンのサイズが正方形ではなかった場合のことを考えての処置です。
GLSL editor ではスクリーンサイズが縦横共に 512px なのでいいのですが、大抵のモニターは横に幅広い縦横比になっていると思います。こういった場合、先ほどのコードのようにminなどをうまく利用しないとレンダリングされた映像が不自然に引き延ばされたような状態になってしまうことがあります。
GLSL editor 以外の環境でもコードの流用ができるように、このような記述になっているのですね。
光のオーブを描いてみる
さて、少々正規化の話が長くなってしまいましたが、最初に座標を正規化してあれば、あとは工夫して光を表現するだけです。
先ほども書いたように座標を正規化したことによって、 スクリーンの中心の位置が原点 になっています。まずこのことを頭に入れておきましょう。
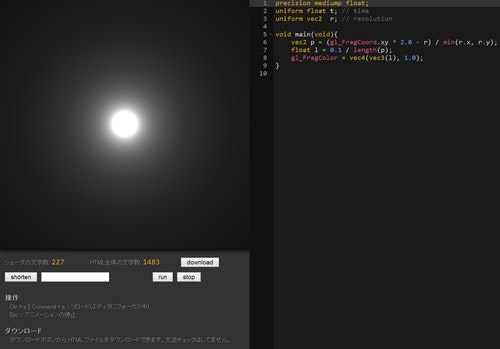
そして、この原点の位置に光のオーブを出すコードが次のようになります。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y); // 正規化
float l = 0.1 / length(p);
gl_FragColor = vec4(vec3(l), 1.0);
}
さて、これを実行するとどのような結果になるのかというと……
こんな感じになります。
見事に光り輝く丸い玉のようなものが画面に出ています。
こんな短いコードでこんな映像が出るのですから不思議ですね。
どうしてこのような結果が得られるのかを知るためには、コードの中で float 型の変数 l に値を入れている箇所について理解しないといけませんね。
該当するコードの部分だけを再度抜粋してみます。
float l = 0.1 / length(p);
さて、これを見ると初めて出てきた関数がありますね。length という関数がそれです。
この関数は、超いろいろ端折って簡潔に言うと、その名前からもわかる通り長さを計算してくれる関数です。
もう少し踏み込んで言うと、今回の例で言うならば 原点からどれくらいの距離があるか を計算してくれる関数だと考えるといいかもしれません。
※厳密な意味はいずれまた解説しますね
なぜ光のオーブのように見えるのか
length は先ほども書いたように、原点からどのくらいの距離があるのかを計算して返してくれます。
つまり、正規化済みの座標を渡すと、それが原点からどのくらい離れているのか、教えてくれるわけですね。
原点の位置は、スクリーンの中央部分です。そこから離れれば離れるほど length の戻り値は大きくなります。そして、その原点からの距離を使って 0.1 / length(p) のような計算をすると、どうなるのでしょう。
たとえば、0.1 / 1.0 を計算するとどうなるでしょう。この場合は言うまでもなく答えは 0.1 ですね。それでは 0.1 / 0.5 だとどうでしょうか。これを計算すると答えは 0.2 になりますね。ではさらに右項を小さくして 0.1 / 0.1 を計算したらどうなるでしょうか。
これは 1.0 になります。
つまり、0.1 を割り算する計算では、割る数が小さくなればなるほど答えは逆に 大きな数字になる わけですね。
こうして考えてみると……
- 原点はスクリーンの中央
- 原点に近いほど
lengthの戻り値は小さい - 0.1 を割る数が小さいほど計算結果は大きい数字になる
というわけで、原点に近ければ近いほど、結果的に計算結果(変数 l の中身)は大きな数字になるわけです。
これをそのまま RGB の値として出力しているので、スクリーンの中央、つまり原点に近い位置ほど色が強烈に明るくなり、そこから離れれば離れるほど暗くなっていくということだったんですね。
前回の内容を参考にアニメーションさせてみる
さて、光のオーブが出る仕組みはわかりました。
前回、せっかくアニメーションするための基本を習得したので、今回の内容との合わせ技で光の量が時間の経過によって変化するようにコードを修正してみましょう。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
float l = 0.1 * abs(sin(t)) / length(p);
gl_FragColor = vec4(vec3(l), 1.0);
}
さて、どこかどう変化したかわかるでしょうか。
変更したのは一行だけ、length 関数を使っているところのコードですね。
先ほどまでは 0.1 / length(p) となっていたところを、0.1 * abs(sin(t)) / length(p) というように修正しました。
これを GLSL editor に貼りつけて実行してみてください。見事に光の広がり具合がアニメーションして変化するようになったはずです。
今までとは違い、だいぶ見栄えのするものができるようになったのではないでしょうか。
さて、次回はもう少し踏み込んで、この光のオーブがスクリーン内を変幻自在に動き回るようにしてみましょう。
お楽しみに!
次回:[連載]やってみれば超簡単! WebGL と GLSL で始める、はじめてのシェーダコーディング(5) - Qiita