まずは挑戦してみよう
シェーダを自分でコーディングするなんて……
きっとお難しいんでしょ……
と、お思いの奥様方。そんなことはないんです。コツをつかめば意外と楽しめます。当連載では、シェーダというものに対して抱かれてしまいがちな、漠然とした 難しそう感 を払拭すべく、簡単なシェーダの記述とその基本について解説したいと思います。
前回:[連載]やってみれば超簡単! WebGL と GLSL で始める、はじめてのシェーダコーディング(4) - Qiita
想定する読者
当連載では、シェーダってなんか難しそう……とか、シェーダプログラミング始めてみたいけど……とか、なんとなく興味を持ってるけどシェーダを記述したことがない方を読者に想定しています。
たとえば Unity などのツール、あるいはマインクラフトのようなゲーム、またはモデリングソフトなどでもシェーダを自分で記述することができるような世の中です。きっとシェーダに触れた経験は無駄にはならないでしょう。
すぐに業務で活かすとか、そういう壮大な話はさておいてまずは気軽にシェーダに触れてみましょう。
難しい 3D の数学的知識はとりあえず要りません。もちろん難しいことをやろうとする場合は話が変わってきますが、当連載ではそのあたりの知識は求めません。ちょっとくらい、三角関数とかは出てきますがそんなに難しくないですから安心してください。
対象のシェーダ記述言語は GLSL
「シェーダ」という言葉には非常に広い意味が含まれるので、世の中にはシェーダといってもいろいろなものが存在しています。また、それを記述するための専用の言語にも、いくつか種類があったりして非常に初心者には敷居が高いのかなと思います。
当連載では GLSL というシェーダ専用言語を用います。
GLSL は 昨今話題の WebGL でも採用されているので、特別な開発環境の準備などをしなくても、ブラウザとテキストエディタさえあれば簡単に始められます。
また、当連載では著者自作の GLSL editor というオンラインでシェーダが記述できるエディタを使いますので、もはやブラウザとネット環境さえあればシェーダが書けます。気軽ですね。
それでは早速、前回に引き続き、シェーダプログラミングについて考えていきましょう。
光の表現を動かす
前回は光のオーブをレンダリングして、今までとはちょっと違って、多少見栄えのする感じになりました。
また、前々回の内容を踏襲しつつ光の強さが時間の経過によって変化するようにアニメーションも付けたりしましたね。
ここまで来ると、だいぶシェーダコーディングの基本が身についてきています。今回の内容までを習得すれば、もうその気になれば自分で工夫してシェーダが記述できるくらいにはなっていると思います。
頑張って取り組んでみてください。
さて、それでは今回は前回のコードを修正しながら、もう少しレンダリング結果に動きをつけてみます。前回のコードでは、光の強さを時間の経過によって変化させましたが、光のオーブがレンダリングされる位置はスクリーンの中央に固定されていました。
これをまずは任意の座標に動かせるようにしてみます。
length 関数の本当の意味
前回から登場している GLSL の組み込み関数である length ですが、この関数が何をやってくれるものなのか、先に確認しておきましょう。
3D の世界では数学の知識が欠かせません。ベクトルとか、行列とか、あまり 3D や数学的なことに詳しくない人でも、もしかしたら耳にしたことがあるかもしれません。
これらのいかにも難しそうな数学の知識は、絶対にないと困るというものでもないのですが、多少なりとも理解していたほうが何かといろいろな場面で役に立ちます。今まさに解説しようとしている length 関数も、実はベクトルと深いかかわりのある関数なんです。
ここで難しそうだと匙を投げるのは簡単ですが、実際は全然難しくないですからちょっと考えてみましょう。
ベクトルというのは、いろいろ数学的なことを言い始めると確かに面倒というかわかりにくい部分もあるのですが、超簡単に理解するなら 向き+大きさ(長さ) を表すものだと考えるのがいいですね。
- 向き
- 大きさ(長さ)
上記の二つの情報を表すのに、当連載でもたびたび登場している vec 系の型を用います。
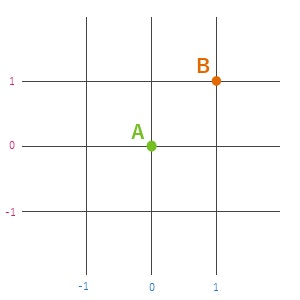
例えば、次のようなマス目で区切られたフィールドがあるとしましょう。
A という地点と B という地点、二つの座標がマス目上にあります。
このとき、A から B までの距離を表現したいとしたら、どんな風に表現したらいいでしょうか。
もし言葉で書くなら「右に1マス進んで上に1マス進む」と言えばいいでしょうか。これを数字だけで表したいわけです。横方向が X で縦方向が Y と考えると、これをこんな風に表現したら数字だけで表すことができそうだとは思いませんか?
v = (1, 1) ← X 方向に 1 移動して Y 方向に 1 移動する
すごく簡単に言うと、これこそがベクトルなんですね。A から B へ向かいたいとき、その方向を数字で表したもの、これがベクトルです。
今回の例では平面上にある A と B という二つの地点なのでベクトルも二次元で (横, 縦) のように書きましたが、これが三次元であれば (横, 縦, 奥行) という風に書けばいいんですね。
これでベクトルが方向を表すために利用できることはわかりました。しかし、ベクトルにはもう一つ、大きさを表す役割もあります。これはいったいどういうことなんでしょうか。
長さが知りたい!
先ほどのベクトルの例では、横と縦にそれぞれ 1 マス進むことで A から B に向かうベクトルを表現しました。しかし一方で、ベクトルの「大きさ」というのはどういうことなんでしょう。
たとえば先ほどの図を十倍して、A 地点はそのまま、B 地点が (10, 10) にあると想像してみてください。
この場合も、よくよく考えてみると A 地点から B 地点までの方向は同じですよね。変わっているのは方向ではなくて単純に距離です。
つまり、(1, 1) であっても (10, 10) であっても、はたまた (3, 3) であっても、これらのベクトルが指し示している 方向はいずれもまったく同じ です。違うのは、その距離ですよね。これこそがベクトルが大きさを表現できるという意味だったんです。
ちょっとわかりにくいかもしれませんが、落ち着いて考えてみましょう。
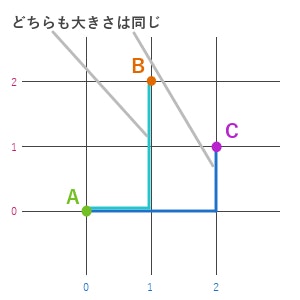
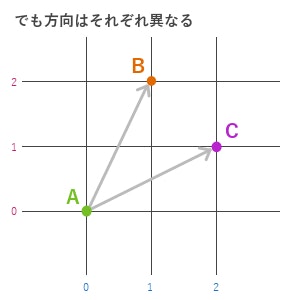
ベクトルは、先述のとおり「方向」と「大きさ」を表すことができます。方向は、要素同士の比率によって決まります。(1, 2) と (2, 1) では、指し示している方向が違っていますよね。
一方でベクトルの大きさは、単純に要素の大きさで決まります。(1, 2) というベクトルと (2, 1) というベクトルは同じ大きさです。これは以下の図を見るとわかりやすいと思います。方向は違っていますが、大きさは同じですね。
では先ほど図解したように、ベクトルで方向や大きさが表現できることはわかりました。しかし、二つの地点の間の距離を知りたい場合にはどうしたらいいでしょうか。
A と B という二つの地点を結ぶベクトル表現はわかりましたが、二点間の距離はベクトルを見ただけではわかりませんね。
ここで登場するのが length 関数です。
この関数は、A 地点が (0, 0) の状態、つまり始点が原点にある状態と仮定したときに、B 地点までどのくらいの距離があるのかを計算して返してくれます。
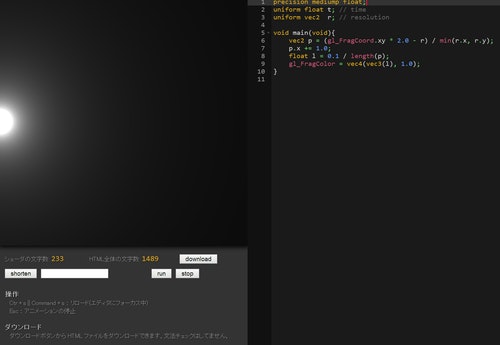
前回のシェーダでは、光のオーブが画面の中央に置かれている状態になっていました。これは、前回のコードを length の意味を踏まえて見てみればおのずとわかるのではないでしょうか。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
float l = 0.1 / length(p);
gl_FragColor = vec4(vec3(l), 1.0);
}
main 関数の冒頭一行目では、gl_FragCoord の値を利用して座標を正規化していたのでしたね。結果、変数 p の中には -1 ~ 1 の範囲の数値が得られるのでした。
そして length は A 地点を原点 (0.0, 0.0) として、引数に与えられた B 地点までの距離を測ってくれます。
length が原点からの距離を計測してくれるのだということがわかっていれば、光のオーブの位置を自由自在に動かすことができるようになります。要は、うまく差分を計算してやったうえで length に座標を与えてやるようにすればいいのです。
オーブを移動させる
それでは先ほどのコードの一部を、次のように変更したらどうなるのか、考えてみてください。
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
p.x += 1.0; // ← 正規化済みの座標の X に 1.0 を足す
float l = 0.1 / length(p);
gl_FragColor = vec4(vec3(l), 1.0);
}
正規化された座標が格納されている変数 p の X 要素に、1.0 を加えています。
1.0 を加えた状態の座標をそのまま length 関数に渡していますが、このようにするとレンダリング結果にはどのような変化が起こるのでしょうか。
正解は……
以下のようになります。
光のオーブが左側に移動しましたね!
先ほどのように、正規化済みの座標に 1.0 を加算した場合、本来 0.0 だった場所は 1.0 になり、同様に本来は -1.0 だった場所が 0.0 になります。
つまりこれを言い換えると、1.0 を加算したことによって、 本来は -1.0 だった場所が原点と同じ扱いになってしまった ということです。
そう考えてみると、光のオーブが左側に移動してしまったのも納得できますね。
そしてこれを応用すれば、光のオーブを右に寄せたり、あるいは上下に寄せたりするのも簡単です。数字を足したり引いたりするだけで、自在に原点の位置をオフセットして、光のオーブを移動させることができるようになったわけです。
サインやコサインを使って動かす
それでは最後に、サインやコサインをうまく利用して、光のオーブをスクリーン内のいろんなところに移動するようにシェーダのコードを改造してみましょう。
以前の連載記事でも書きましたが、サインやコサインを使うと時間の経過による処理を簡単に行うことができるようになります。三角関数を応用することで、アニメーション処理が楽になるのですね。
今回は光のオーブが曲線を描きながら画面内を移動するようにするため、以下のようにコードを書いてみましょう。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
p += vec2(cos(t), sin(t)) * 0.5;
float l = 0.1 / length(p);
gl_FragColor = vec4(vec3(l), 1.0);
}
main 関数の二行目でサインとコサインが出てきていますね。
先ほど解説したのと同じように、正規化済みの変数 p に、サインやコサインによって得られた値を加工してから加えています。
おさらいすると、sin や cos は引数にどのような値を与えられても、そこからサインやコサインを計算して -1 ~ 1 までの範囲の値を返してきます。そこから得られた値を変数 p に加えてやるわけですね。
上記のコードを実行すると、光のオーブが原点を中心に円を描くように移動するようになったはずです。実際に GLSL editor に貼りつけて実行してみるとわかると思います。
では、次のようなコードだったらどうでしょうか。
この場合はどんな動きになるか、実行する前にコードをよく見て予想してみてください。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
p += vec2(cos(t * 5.0), sin(t)) * 0.5;
float l = 0.1 / length(p);
gl_FragColor = vec4(vec3(l), 1.0);
}
どのような結果になるのかは、自分なりに予想を立ててから、実際に実行して確かめてみてください。
サインやコサインの使い方を覚えておくと、いろいろな場面で役に立つのでオススメです。
さて、今回はここまでです。
次回は、光のオーブから発展して、もう少し複雑な図形を描いてみましょう。また、繰り返し処理についても触れる予定です。
お楽しみに!
次回:[連載]やってみれば超簡単! WebGL と GLSL で始める、はじめてのシェーダコーディング(6) - Qiita