まずは挑戦してみよう
シェーダを自分でコーディングするなんて……
きっとお難しいんでしょ……
と、お思いの奥様方。そんなことはないんです。コツをつかめば意外と楽しめます。当連載では、シェーダというものに対して抱かれてしまいがちな、漠然とした 難しそう感 を払拭すべく、簡単なシェーダの記述とその基本について解説したいと思います。
前回:[連載]やってみれば超簡単! WebGL と GLSL で始める、はじめてのシェーダコーディング(5) - Qiita
想定する読者
当連載では、シェーダってなんか難しそう……とか、シェーダプログラミング始めてみたいけど……とか、なんとなく興味を持ってるけどシェーダを記述したことがない方を読者に想定しています。
たとえば Unity などのツール、あるいはマインクラフトのようなゲーム、またはモデリングソフトなどでもシェーダを自分で記述することができるような世の中です。きっとシェーダに触れた経験は無駄にはならないでしょう。
すぐに業務で活かすとか、そういう壮大な話はさておいてまずは気軽にシェーダに触れてみましょう。
難しい 3D の数学的知識はとりあえず要りません。もちろん難しいことをやろうとする場合は話が変わってきますが、当連載ではそのあたりの知識は求めません。ちょっとくらい、三角関数とかは出てきますがそんなに難しくないですから安心してください。
対象のシェーダ記述言語は GLSL
「シェーダ」という言葉には非常に広い意味が含まれるので、世の中にはシェーダといってもいろいろなものが存在しています。また、それを記述するための専用の言語にも、いくつか種類があったりして非常に初心者には敷居が高いのかなと思います。
当連載では GLSL というシェーダ専用言語を用います。
GLSL は 昨今話題の WebGL でも採用されているので、特別な開発環境の準備などをしなくても、ブラウザとテキストエディタさえあれば簡単に始められます。
また、当連載では著者自作の GLSL editor というオンラインでシェーダが記述できるエディタを使いますので、もはやブラウザとネット環境さえあればシェーダが書けます。気軽ですね。
それでは早速、前回に引き続き、シェーダプログラミングについて考えていきましょう。
複数のオーブが宙を舞う
前回の連載記事では、光のオーブを複雑に移動させる方法について扱いました。
サインやコサインといった三角関数を利用することで、かなり面白い動きを付けることができるのでしたね。
今回は、前回の内容を踏襲しつつ、まずは、より見た目にインパクトのある物量感を出してみましょう。前回まではオーブの個数が一個だけでしたが、これを複数個出せるようにしてみます。
今回はいきなりコードを掲載してしまいましょう。
前回もそうでしたが、まずはコードを見て、どんなふうにレンダリングされるのか想像してみるといいかもしれません。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
vec3 destColor = vec3(0.0);
for(float i = 0.0; i < 5.0; i++){
float j = i + 1.0;
vec2 q = p + vec2(cos(t * j), sin(t * j)) * 0.5;
destColor += 0.05 / length(q);
}
gl_FragColor = vec4(destColor, 1.0);
}
さて、このコードを実行するとどんな見た目になるんでしょうかね。
気になるところですが、まずは今回のコードで初めて登場した概念である for 文による繰り返し処理について触れておきます。
GLSL の for ステートメント
javascript などと基本的には同じ文法で書くことができる for 文ですが、GLSL 特有の注意事項がいくつかあります。
まず、初期化の時点で次のように書くと、これがエラーになるんですがどうしてだか想像つくでしょうか。
float j = 5.0;
for(float i = 0.0; i < j; i++){
// 何かの処理
}
普通に考えると何もおかしなところは無いように見えますよね……
でもこれはコンパイルが通りません。
どうしてかというと、ループの継続を判断する条件式の部分に、変数(上記の場合でいうと j)を使っているから NG なんですね。
GLSL における for 文の初期化では、継続判定の条件式にはコンパイル前に不定の値は利用できません。つまり、ここに関してはハードコーディングが必要ということです。
ですから次のようにすればエラーは起こりません。
for(float i = 0.0; i < 5.0; i++){
// 何かの処理
}
これだったら大丈夫です。
あとは、次のような書き方もダメです。
for(float i = 0.0; 5.0 < i; i++){
// 何かの処理
}
些細な違いなんですけどね……
とにかく書き方に厳密なルールがあるということは確かです。for 文による繰り返し処理を記述する際は、このあたり注意しましょう。
また、今回は掲載したコードの性質的に、繰り返し処理のカウンタとして一般的な int 型の整数ではなく float を使っていますが、ここで float でなくてはいけないということはありません。
むしろ、普通は int で繰り返し処理を記述したほうがいいでしょう。
ただ、たとえばそのカウンタの値によって係数が変化したりするような処理を書く場合、型のキャストが問題になることがあります。
以前の連載テキストでも書きましたが、整数型と浮動小数点型のデータを同時に計算に使おうとすると、GLSL ではエラーが発生してコンパイルが通りません。
for(int i = 0; i < 5; i++{
float f = i + 1;
}
たとえば上記のような記述は、整数と浮動小数点数データとが混在しているためエラーになってしまいます。
カウンタの役割を持つ変数 i が計算に利用できないのは不便ですよね。そこで、こういった場合には意図的に型をキャストするための文法を利用します。
明示的にキャストを行う場合には次のように書きます。
float f = float(i + 1);
C 言語などの場合は、キャストするのに (float)i といった書き方をしますね。GLSL は文法が C 言語とよく似ている割に、このような型のキャストはできません。イメージとしては、上記のコードで示したように型キャスト用の関数があって、その引数に値を渡すような感じになるんですね。
複数の光のオーブ
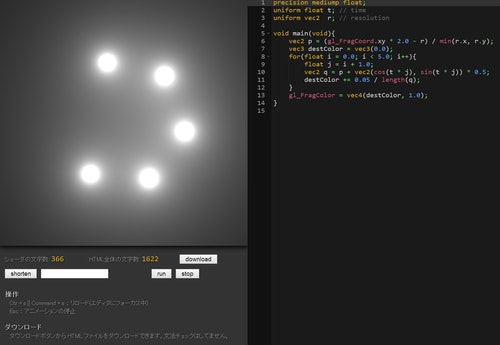
さて、for 文について理解できたら、冒頭で掲載したコードの実行結果がどのようになるのか、その様子を見てみましょう。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
vec3 destColor = vec3(0.0);
for(float i = 0.0; i < 5.0; i++){
float j = i + 1.0;
vec2 q = p + vec2(cos(t * j), sin(t * j)) * 0.5;
destColor += 0.05 / length(q);
}
gl_FragColor = vec4(destColor, 1.0);
}
こんな感じになります。
コードをよく見るとわかると思いますが、for 文によって繰り返し処理することで、複数のオーブをレンダリングさせています。
それぞれのオーブは、いずれも円を描くような軌道で移動し続けますが、移動する量を繰り返し処理のカウンタの大きさに応じて変えているので、それぞれが異なる速さでスクリーン内を移動するようになっています。
実際に GLSL editor で実行してみればわかると思いますが、光の強さは単純に for 文内では加算するように処理しているため、オーブ同士が座標的に重なっている場合にはかなり光の表現が強くなります。
これを工夫して改造することができたら、メタボールのような表現をすることもできそうですよね。
オーブ以外の光の形状
さて、光のオーブ、そしてオーブを複数描く、といったことができるようになりました。
これだけでも、オーブの移動する軌道や速さを変えるだけでかなり遊べます。また現状は完全に色を白黒で表現していますが、RGB をうまく調整すると非常にキレイな見た目にできるのでいろいろ調整してみると楽しいです。
ですか、オーブしか描けないのはちょっと味気ないので、比較的概念の簡単なリング状の光の輪にもチャレンジしてみましょう。
光の輪を描く仕組みは、実はオーブの概念をほんの少し工夫して修正すればいいのです。
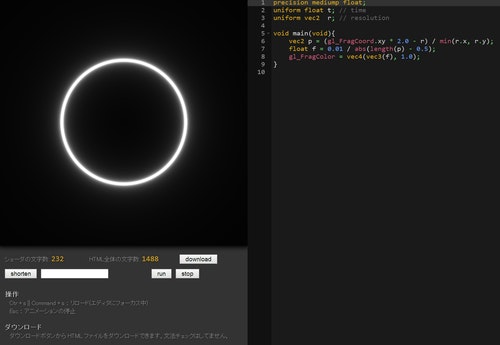
今度はこれまでとは逆に、コードはまだ掲載しませんが結果だけを見てみます。
どのようなコードを書いたら、こんな結果が得られるのでしょうね。
よーーーく見たらコード見えちゃいそうですけどそこはノリで!
このように、同じような光の表現を用いつつ、輪を描くように光を分散させるにはどうしたらいいか、想像がつくでしょうか。
ポイントになるのは、オーブをレンダリングするときに、どのような計算をして光の強さを調整していたのかをよく考えることですね。
まずは、オーブの場合のコードを再度掲載してみましょう。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
float f = 0.1 / length(p);
gl_FragColor = vec4(vec3(f), 1.0);
}
はい、これがオーブを描いた場合の GLSL のコードです。
ポイントは float 型の変数 f に値を代入している部分でした。
length 関数は原点からどのくらい離れているのか、その距離を返してくれる関数でした。原点に近ければ近いほど小さい値を、遠ければ遠いほど大きい値を返すわけです。
その数値を使って 0.1 を除算すると、結果的に原点に近い場所ほど光が強くなるという仕組みでしたね。
輪のような形に光を広げたいとすると、原点から 一定の距離にある場所ほど小さい値になる ようにしてやり、その数値を使って除算すればいいということになります。
ちょっとわかりにくいですね。
でも焦らずに考えてみましょう。
たとえば、原点(0.0, 0.0)から 0.5 離れた距離にある場所にリングを出したいとします。
その場合、length の戻り値が 0.5 になる場所ほど、計算結果が 0.0 に近づくようにすればいいわけです。
もう一度言います。length の戻り値が、0.5 に近づけば近づくほど、計算結果が 0.0 に近くなるような計算の方法を考えればいいんです!
はい、それではそろそろ正解のコードを掲載してみます。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
float f = 0.01 / abs(length(p) - 0.5);
gl_FragColor = vec4(vec3(f), 1.0);
}
さて、どうでしょう。
先ほどと同様に length が使われているコードをよく見てみてください。
length の戻り値から 0.5 を減算して、さらにそれを abs で包んでいますね。先ほども書いたように、輪のような模様を出すためには length の戻り値が 0.5 に近い場所ほど計算結果が 0.0 に近づくようにすればいいわけですから、上記のように単純に 0.5 を減算してやればいいのですね。
abs で包んでいるのにもちゃんと理由があって、もしこれを abs なしでやった場合には次のような感じになっちゃいます。
これ、画像でわかりますかね。
リングの内側だけ、ぼんやりとしたブラーが掛かっておらず、バッサリと黒一色になってしまっています。
よく考えてみればわかると思いますが、length はあくまでも原点からの距離を返してくるだけなので、abs を併用しない場合には当然、0.5 を引いたときに負の数値になってしまう領域が出てきます。
負の数値を計算に利用してしまったら、当然変数 f に入る値も負の数値になってしまうので、結果的に色が真っ黒になってしまうのですね。
輪の内側にも外側にも、ぼんやりと光のあふれたような表現をするためには、abs の存在が実は重要だったわけですね。
さあここからは応用だ!
さて、光の輪を出すためのコードがわかりました。
となると、ここまでの連載で扱ってきた for 文や、時間の経過によるアニメーションを駆使すると、かなりいろいろなことができるようになるはずです。
参考までに、ここまで紹介してきたテクニックを駆使して、もう少し見た目にインパクトのあるシェーダを書いてみました。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
vec3 destColor = vec3(1.0, 0.3, 0.7);
float f = 0.0;
for(float i = 0.0; i < 10.0; i++){
float s = sin(t + i * 0.628318) * 0.5;
float c = cos(t + i * 0.628318) * 0.5;
f += 0.0025 / abs(length(p + vec2(c, s)) - 0.5);
}
gl_FragColor = vec4(vec3(destColor * f), 1.0);
}
ちょっと複雑に見えますか?
でも、今まで解説してきたことの組み合わせだけでほとんどできています。
しいて言うなら、コードの中に出てきている謎の数字、0.628318 ですが、これは円周率を五分の一にした数値です。どうして円周率を五分の一にした数値を使って今回のコードを書いたのかは、次回以降、簡単に解説しようと思います。
実際に GLSL editor に貼りつけて実行してみると、面白いものが見れると思いますよ。
それでは第六回はここまで。
次回もお楽しみに!
次回:[連載]やってみれば超簡単! WebGL と GLSL で始める、はじめてのシェーダコーディング(7) - Qiita