まずは挑戦してみよう
シェーダを自分でコーディングするなんて……
きっとお難しいんでしょ……
と、お思いの奥様方。そんなことはないんです。コツをつかめば意外と楽しめます。当連載では、シェーダというものに対して抱かれてしまいがちな、漠然とした 難しそう感 を払拭すべく、簡単なシェーダの記述とその基本について解説したいと思います。
前回:[連載]やってみれば超簡単! WebGL と GLSL で始める、はじめてのシェーダコーディング(6) - Qiita
想定する読者
当連載では、シェーダってなんか難しそう……とか、シェーダプログラミング始めてみたいけど……とか、なんとなく興味を持ってるけどシェーダを記述したことがない方を読者に想定しています。
たとえば Unity などのツール、あるいはマインクラフトのようなゲーム、またはモデリングソフトなどでもシェーダを自分で記述することができるような世の中です。きっとシェーダに触れた経験は無駄にはならないでしょう。
すぐに業務で活かすとか、そういう壮大な話はさておいてまずは気軽にシェーダに触れてみましょう。
難しい 3D の数学的知識はとりあえず要りません。もちろん難しいことをやろうとする場合は話が変わってきますが、当連載ではそのあたりの知識は求めません。ちょっとくらい、三角関数とかは出てきますがそんなに難しくないですから安心してください。
対象のシェーダ記述言語は GLSL
「シェーダ」という言葉には非常に広い意味が含まれるので、世の中にはシェーダといってもいろいろなものが存在しています。また、それを記述するための専用の言語にも、いくつか種類があったりして非常に初心者には敷居が高いのかなと思います。
当連載では GLSL というシェーダ専用言語を用います。
GLSL は 昨今話題の WebGL でも採用されているので、特別な開発環境の準備などをしなくても、ブラウザとテキストエディタさえあれば簡単に始められます。
また、当連載では著者自作の GLSL editor というオンラインでシェーダが記述できるエディタを使いますので、もはやブラウザとネット環境さえあればシェーダが書けます。気軽ですね。
それでは早速、前回に引き続き、シェーダプログラミングについて考えていきましょう。
美しい花のような模様の秘密
前回の最後に掲載したコード。
何やら怪しげな数値を使って計算を行っていました。あれが一体なにをするためのものだったのか、簡単に説明しようと思います。
まずは、前回の最後に掲載したコード見てみましょう。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
vec3 destColor = vec3(1.0, 0.3, 0.7);
float f = 0.0;
for(float i = 0.0; i < 10.0; i++){
float s = sin(t + i * 0.628318) * 0.5;
float c = cos(t + i * 0.628318) * 0.5;
f += 0.0025 / abs(length(p + vec2(c, s)) - 0.5);
}
gl_FragColor = vec4(vec3(destColor * f), 1.0);
}
一見するとすごく複雑なことをやっているように見えますね。
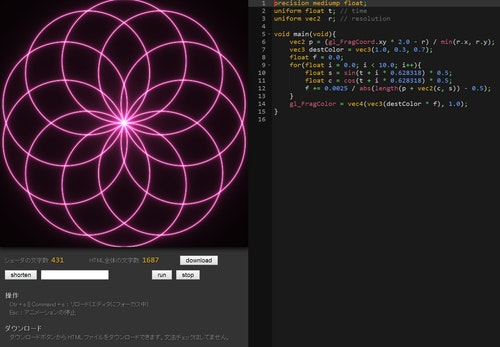
これ、実際に実行してみるとどうなるか、これを読まれている方の中に実際に GLSL editor に貼りつけて動作させてみたという人はいるでしょうか。このコードを実行すると、以下のような見た目の映像が出てきます。
※実物はアニメーションします
あらまあ、これは綺麗ですね。
どうして先ほどのコードでこんな模様が出るのかは、段階を追って考えていくとわかると思います。ポイントになるのは、for 文による繰り返し処理の中でなにが起こっているのかを理解することです。
float f = 0.0;
for(float i = 0.0; i < 10.0; i++){
float s = sin(t + i * 0.628318) * 0.5;
float c = cos(t + i * 0.628318) * 0.5;
f += 0.0025 / abs(length(p + vec2(c, s)) - 0.5);
}
さて、該当する部分を抜粋しました。
for 文による繰り返しは、初期化部分の式を見ると 10 回ループするようになっているのがわかりますね。レンダリング結果を見ても、リングが 10 個出ています。つまりループ 1 回につき 1 個のリングが描かれるようになっているわけです。
そして前回の連載記事の最後でもちょっとだけ触れた、謎の数値 0.628318 ですが、これは円周率を五分の一にしたものだと前回書きました。
なんで円周率?
しかもなんで五分の一?
謎ですね。
この謎を解くためには、ちょっとだけ聞きなれないキーワードについて理解する必要があります。そのキーワードとは、 ラジアン です。
ラジアンとはなんぞや
ラジアンを数学的に、厳密に、解説するつもりはありません。
簡単ですからちょっとだけ頑張ってください。
まず、円周率は 3.14159... でおなじみのあれです。これを記号で表すと π になり、読み方は「パイ」です。これはみなさん算数でやった記憶が結構残ってる言葉なんじゃないかなと思います。
そしてラジアンとは、このパイを使って角度を表現するときに使います。
普通、角度を表現するときって、~~度、みたいな言い方をしますね。これは 度数法 という角度の表現方法で、度数法だと 360 度でぐるりと円形に一周します。
度数法のぐるりと一周、つまり 360 度を、同じようにラジアンで表すとどうなるかというと……
ラジアンのぐるり一周は 2パイ です。
つまり 2π ですね。
要はどういうことかというと、ラジアンで角度を表現するときは 0 ~ (2 * 3.14159...) の範囲で角度を表現します。度数法の 180 度だったら、2π が 360 度に相当するわけですから……そう、πですね。
じゃあ、度数法で 90 度だったら?
もう簡単ですね。0.5πです。
ここまでくると、前回の最後に掲載したシェーダのコードで、パイの五分の一に相当する 0.628318 を使っていた理由がわかりませんか?
度数法の 360 度が 2πですから、パイの五分の一は、360 度の十分の一ですね。先ほどのシェーダの実行結果では、リングが 10 個出ていました。それらの 10 個のリングは等間隔に綺麗に並んでいますよね。これはつまり、0.628318 という数値の正体が、ラジアンをうまく利用してリングをそれぞれ等間隔に 10 個レンダリングするための数値だった――ということなんですね。
ラジアンがわかってると何がうれしいのか
ラジアンは三角関数、つまりサインやコサインと深い関わりを持っています。
たとえば、今までこんなコードを何回か書いてきましたね。
float f = sin(t); // t は time
この、サインの中に時間の経過を入れるタイプの記述は、何度か自分で使ったことがあればわかると思いますが、規則正しく反復するような動きになることが多いはずです。
そして、その反復する時間は、おおよそ 6.3 秒くらいで 1 ループするはずです。
どうしてかというと sin や cos は、その引数に ラジアンを受け取る ことを想定して実装されてるからです。
先ほども書いたように、度数法で言うところの 360 度は、ラジアンで表すと 2πです。ということは、経過時間が約 6.3 秒(2 * π)でちょうど一周するようになるんですね。コンパスで円を描くときに 360 度ぐるりと回したら元の位置にペン先が戻ってくるのと同じように、時間の経過が 2π倍になったときに、ちょうどループが一周して最初の位置に戻ってくるような、そんな動き方をするわけです。
このように、ラジアンがどういったものなのかを、なんとなくでもわかっているといろいろな面でスムーズに理解が得られる場合があります。また、ラジアンの求め方などの、ちょっと踏み込んだ数学的知識も、ないよりははるかにあったほうが有利でしょう。
ラジアンについて少しでも興味が湧いたなら、興味を持ったこのタイミングで勉強してしまうのがいいのではないかなと思います。絶対に今後シェーダコーディングを行っていくうえで役に立ちますしね。
簡単な記述で思わぬ図形が出てくる不思議
さて、ラジアンに関するちょっと小難しい話が続きましたが、ここからは路線を少し変えていきましょう。
サインやコサイン、あるいは length 関数や、mod 関数、abs 関数など、これまでの連載で登場してきた初歩的な関数たち。実は、現状すでに登場しているこういった基本的な関数などを組み合わせるだけでも、結構いろんな図形や模様が描けるのがシェーダコーディングの面白いところです。
ここからは、こういった比較的簡易なロジックの組み合わせで描画できる、いくつかの模様のプリセットを紹介していきましょう。
まずは、こんなコードはどうでしょうか。
※以下、main 関数の中身だけ掲載しますね
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
float f = p.x * p.y;
gl_FragColor = vec4(vec3(f), 1.0);
}
すごく簡易ですね。正規化した座標が入っている変数 p の、X 要素と Y 要素を掛け算しているだけという、なんとも簡単なコードです。
でも、これでどんな映像が出るのかは実行してみないとわからないかもしれませんね。
出し惜しみはせずに、見せちゃいましょう。
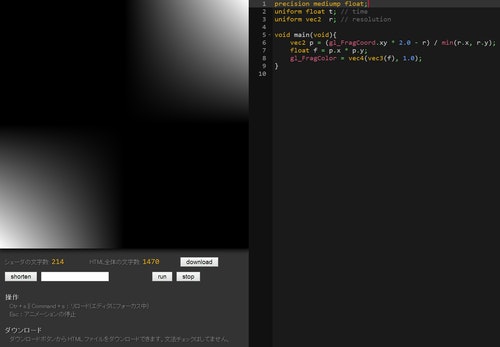
こんな感じになります。
なんだか角だけ色がついてます。
よくよく考えてみればわかりますね。座標同士を掛け算しているので、符号が同じ座標同士が掛け算される部分だけ、色がつくわけです。
では、続いてこれに少し手を入れて、こんな感じにするとどうなるでしょう。
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
float f = abs(p.x) * abs(p.y); // ← X と Y を abs 関数に通す
gl_FragColor = vec4(vec3(f), 1.0);
}
これのポイントは、先ほどの変数 p の各要素を abs を通して絶対値に変換している点です。
マイナスの数値になる座標も、これで強制的にプラスに変換されますので、先ほどまでは色がついていなかった部分にも、色がつくようになるはずですね。
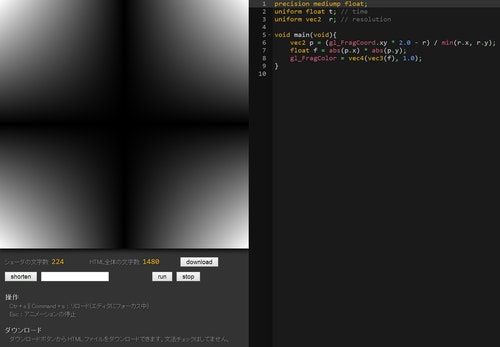
実行すると、こんな感じに。
まだまだ地味ですね……
もう少し改造してみましょう。
続いてはこんな風に修正。
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
float f = 0.001 / (abs(p.x) * abs(p.y)); // ← 0.001 を割る
gl_FragColor = vec4(vec3(f), 1.0);
}
先ほどは、黒い背景のなかで、四隅だけが白っぽく色が塗られたような感じになってましたが……
あれを光のオーブをレンダリングしたときのように、除算に利用してみるとどうなるでしょうか。
勘のいい人だったら、もしかしたらコードを見ただけで想像できたかも?
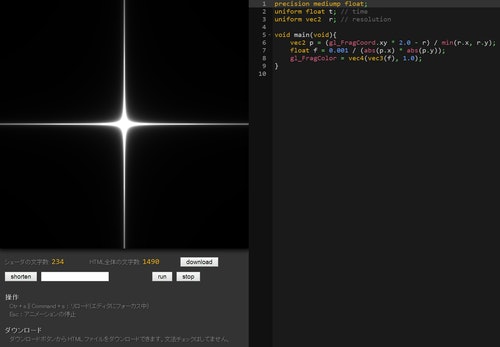
実際に動かしてみるとこんな感じになります。
一気に光っぽい感じになりましたね。
ここまでできたら、あとは座標を動かしてみたり、複数レンダリングして重ねてみたりするだけで、かなり美しい映像が出せるんじゃないでしょうか。
使っているのは、せいぜい掛け算と割り算、そして abs くらいのもんです。
こんな簡単にキレイな映像が出るなんて、面白いですね。
キラシール風シェーダ
さて、もう少し似たようなのやってみましょうか。
先ほどのコードとは括弧の括り方が違うだけの、次のようなコードだとどんなことになるでしょう。
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
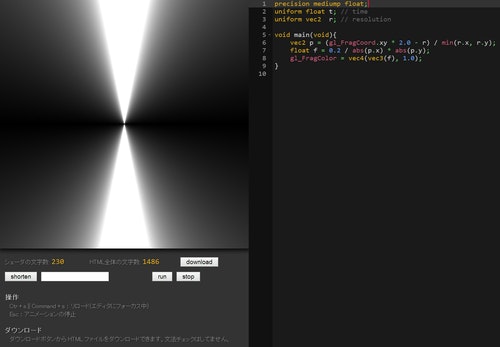
float f = 0.2 / abs(p.x) * abs(p.y); // ←外側の括弧をひとつ外しただけ
gl_FragColor = vec4(vec3(f), 1.0);
}
はい、ほんとに構造的には括弧一つを外しただけですね。
描画結果で光のように見える部分の比率を少し増やした感じにしたかったので、割られる数も 0.001 から 0.2 に変更しました。
たったこれだけの変更で……
見た目はこんな感じになります。
全然違う見た目になりましたね。
この模様、私は初めて目にしたとき思ったんです。
これはビッ●リマンのキラシールの柄やないかい!
でも、こんなにでっかく光の筋が描かれていてもキラシールに見えないので、これを複製してみます。
規則正しく模様を平面上に複製するときには、mod 関数をうまく利用するといいですね。
コードはこんな感じに。
precision mediump float;
uniform float t; // time
uniform vec2 r; // resolution
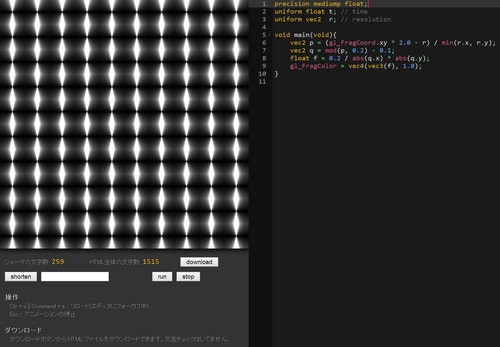
void main(void){
vec2 p = (gl_FragCoord.xy * 2.0 - r) / min(r.x, r.y);
vec2 q = mod(p, 0.2) - 0.1; // mod を通してから一度別の変数に座標を入れる
float f = 0.2 / abs(q.x) * abs(q.y); // その変数を使ってさっきと同じ計算をする
gl_FragColor = vec4(vec3(f), 1.0);
}
コメントにも記載した通り、mod 関数の中に一度変数 p の値を入れて計算し、その結果を別の変数 q にいったん入れておきます。
先ほどの abs を使っているコードの部分には、変数 q のほうを使うようにします。
これでどんな結果になるかと言うと……
こんな感じでズラッと並びます。
mod 関数は、割り算をした余りを返してくれる関数で、GLSL 以外の言語でもよく見受けられるものなので馴染みがある人が多いと思います。
上記のコードのように mod をうまく使ってやると、規則正しく複製されるような座標系を作ることができます。
どうしてこのようなことになるのかは、mod 関数の仕組みがわかっていれば簡単でしょう。
先ほどのコードの場合は、mod(p, 0.2) - 0.1 という計算をしています。この場合、変数 p の中身が大きい数値でも小さい数値でも、mod 関数の効果によって 0.0 ~ 0.19999... の範囲に変換されてしまいます。
そこからさらに 0.1 を減算することによって、結果は -0.1 ~ 0.09999... の範囲にさらに変換されます。こうなると、小さいスクリーンがいっぱい並んでいるのと同じような状態の座標系になるわけですね。その結果、先ほどのレンダリング結果のように、同じ模様がずらりとならんだような状態になるわけです。
いまいちキラシールに見えない?
さて mod 関数を利用してキラシールになるように模様を複製したものの……
正直、まだ全然キラシールに見えませんよね。
でも、これがアニメーションしていたら、その見せ方次第ではキラシールのように見せることができるんです。
ちなみに、それらの変更を加えたお手本コードがあるんですが、これは詳細な解説は次回するとして、実際に動作しているものをご覧いただくことにしましょう。
以下のリンクをクリックすると、GLSL editor に、あらかじめお手本コードが掛かれた状態で表示されます。
お手本コードは本当にキラシールのように見えるのか? 実際に実行して確かめてみてください。
そして、どうやればこのようなアニメーション処理ができるのかは、次回しっかり解説しようと思います。
ポイントは、座標系が 回転している ということです。
この仕組みの詳細については次回!
お楽しみに。
次回:[連載]やってみれば超簡単! WebGL と GLSL で始める、はじめてのシェーダコーディング(8) - Qiita