効果検証入門1章〜3章の読書メモ
セレクションバイアスとRCT
ビジネス現場では何らかの施策(介入、処置)の効果を計測したいというモチベーションがあるが、間違った方法で検証すると分析結果と真の効果に乖離(バイアス)が生じることがある。
特に、介入の効果を測る際に介入グループと非介入グループにおける結果を比較することが多いが、この際、グループ間における潜在的な傾向が違うことによって発生するバイアスをセレクションバイアスと呼ぶ。それゆえ、いかにバイアスを取り除けるかが効果検証における課題となる。
実際には介入を無作為に決定することで、介入以外の背景や要因を平均的に同一にすることが可能である。これをRCT (無作為化比較実験、Randomized Controlled Trial)やABテストと呼ぶ。
理想的な方法は同じサンプル $i$で介入ありの結果 $Y(1)$ と介入なし $Y(0)$ の結果を比較することだが、現実的にはRCTが困難な場合や既に手元にあるデータを用いて分析をしなければならない場合が多い。この様な場合、基本的には同じサンプルではどちらか一方の状態しか観測できない(=反実仮想)。それゆえ、介入グループと非介入グループの平均的な効果について考え、各グループの期待値の差**ATE (平均処置効果、Average Treatment Effect)**を用いる。($τ = E[Y(1)] - E[Y(0)]$ )
因果推論の必要性
ビジネスの場では、分析の都合を最優先したRCTはコストがかかるほか、倫理的な実行可能性の観点で実施が難しいことがある。こういった場合に計量経済学や因果推論が役に立つ。ただしこれらの手法はデータを入力すれば自動で結果が出力されるような代物ではなく、分析者が対象となる事象、特にセレクションバイアスについて正しく理解し分析を設計する必要がある。つまり、分析者が認知していないようなセレクションバイアスを減少することはできない。
ビジネス現場において、バイアスを含んだまま施策の効果を検証し、PDCAのループを回していくことは以下の問題を生み出すことになる。
- 真にKPIを改善しているか分からないものにコストを支払い続ける
- 蓄積される知見の多くがセレクションバイアスの作り方となる
つまり、実行可能ならばRCTを用いた検証、不可能な場合に因果推論などでバイアスの影響が少ない手法で検証することが重要。
回帰分析
介入効果を測るための回帰分析
回帰分析ではYの近似値に加えて、Yの条件付期待値E[Y|X]に対する推定値を得ている。
Y = E[Y|X] + u = \beta_{0} + \beta_{1}X + u\\
Y = E[Y|X, Z] + u = \beta_{0} + \beta_{1}X + \beta_{2}Z + u\\
Y = E[Y|X, Z] + u = \beta_{0} + \beta_{1}X + \beta_{2}X^{2} + \beta_{3}Z + u
- モデルには以下の変数を使用する
- 被説明変数 Y
- 介入変数 Z
- 共変量 X
本来知りたい効果 $E[Y|X, Z=1] - E[Y|X, Z = 0]$ は推定されたモデルのパラメーターを用いて以下の様に算出する
$$
\begin{equation}
E[Y|X, Z = 1] = \beta_{0} + \beta_{1}X + \beta_{2} X_{2} + \beta_{3} \times 1+ u \tag{1}
\end{equation}
$$$$\begin{equation}
E[Y|X, Z = 0] = \beta_{0} + \beta_{1}X + \beta_{2}X_{2} + \beta_{3}\times 0 + u\tag{2}
\end{equation}
$$
(1)から(2)を引くことで $E[Y|X, Z=1] - E[Y|X, Z = 0]$ が求まる。
$$\begin{equation}
E[Y|X, Z=1] - E[Y|X, Z = 0] = \beta_{3}\times 1 - \beta_{3}\times 0 = \beta_{3}
\end{equation}
$$
回帰分析におけるバイアス
回帰分析においてセレクションバイアスを小さく効果の推定をするためには共変量を正しく選択することが重要である。具体的には目的変数$Y$と介入変数$Z$に対して相関のある共変量(交絡因子)を加える。
また、本来は必要なのにモデルから抜けている変数を脱落変数と呼ぶ。脱落変数があるモデルにおける効果は本来の効果に**脱落変数バイアス (OVB : Omitted Variable Bias)**が含まれることになる。
OVB = 省略された共変量X_{omit}とYの相関\times介入変数ZとX_{omit}の相関
仮に脱落変数になり得る変数を加えたモデルの結果としてその推定値が統計的に有意でなくても取り除くべきではない。
基本的には効果を測定するための回帰分析においては介入変数以外に関する有意差検定の結果について気にする必要はない。
Conditional Independence Assumption
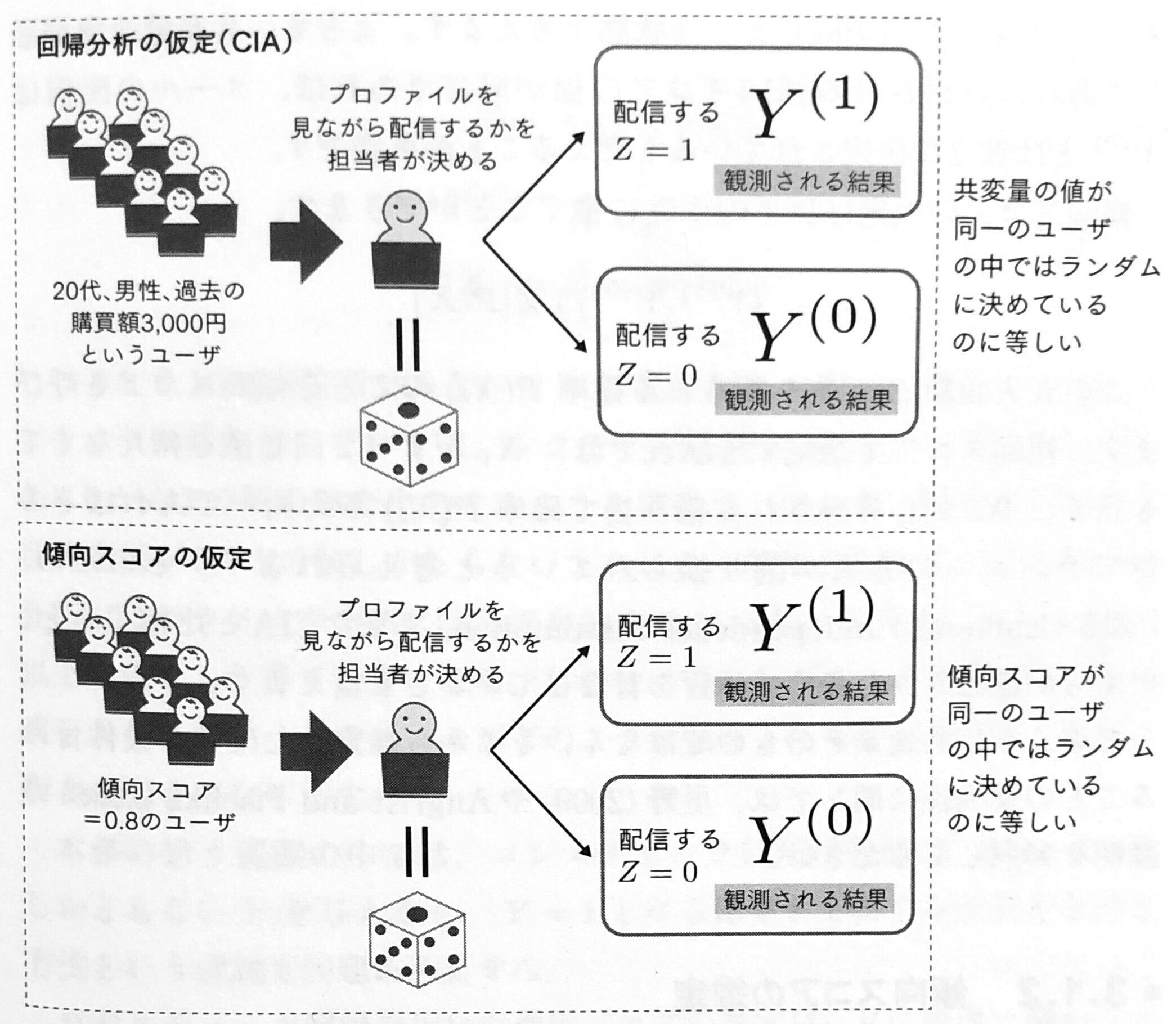
OVBが0になる状態では、共変量で条件付けたとき介入変数が目的変数とは独立な状況であり、**CIA (Conditional Independence Assumption)**と呼ばれる。つまり、共変量の値が同一のサンプルにおいて介入 $Z$ はランダムに割り当てられていることに等しいという考え方である。
効果検証のための回帰分析における分析ステップは以下の様になる。
- どのように介入の割り当てが決定されれるのかを考える
- 決定方法を表現できる共変量を選択する
- 選択した共変量とYの関係を考慮しモデルを決める
実際には上記のステップで分析した際に、CIAが担保できているか評価する際に生じる2つの障壁がある。
1. バイアスの評価
OVBはバイアスがどのように変化するかを示すだけであり、他のバイアスの大きさについては評価できない。それゆえ、分析者が残りのバイアスの発生理由とコントロール可能な共変量を仮定する必要がある。
2. 必要は共変量がデータにない場合
バイアスを発生させる要因がわかったとしてもそれを表現できるデータがなければバイアスを減らすことは不可能である。
Sensitivity Analysisという手法を用いることでデータにない変数がバイアスを起こすか評価することができる。この手法では重要だと考える共変量以外を除去した場合の効果の推定値を確認し、変動が小さければ他の変数による影響を受けにくく、データにない変数による影響も小さいと考える。
Post treatment bias
介入による影響を受ける変数を分析に用いることで生じるバイアスをPost Treatment biasと呼ぶ。これを避けるためには、介入の後のタイミンングで決定する変数を分析から除外することが必要である。
その他の議論
- 効果検証のためのモデルにおいてYに対する予測能力の評価は本質ではない
- 対数をとる場合
- 目的変数に対する介入効果が比率で扱われる必要があるときYの対数をとる
- 共変量と目的変数の関係が比率で扱われる必要があるとき共変量の対数をとる
- 介入変数以外の共変量間における多重共線性は大きな問題とはならない
傾向スコアを用いる方法
傾向スコアのアイデア
回帰分析による効果検証は共変量の選定が重要かつ難しい。傾向スコアとは介入が行われる確率のことで、共変量を用いて介入変数 $Z$ を予測するモデルを構築することで算出する。
- モデル:ロジスティック回帰、GBDTなど
- モデルの結果としては予測値が重要であり、例えばロジスティック回帰におけるパラメータは使用しない
傾向スコアを用いる方法では、介入の割り振り確率で条件付けたサンプル間において、介入が $Y$ とは独立に割り振られていると仮定する。それゆえ、共変量が同じ値を持たなくても良いので回帰分析におけるCIAより緩和された条件となる。
傾向スコアマッチング
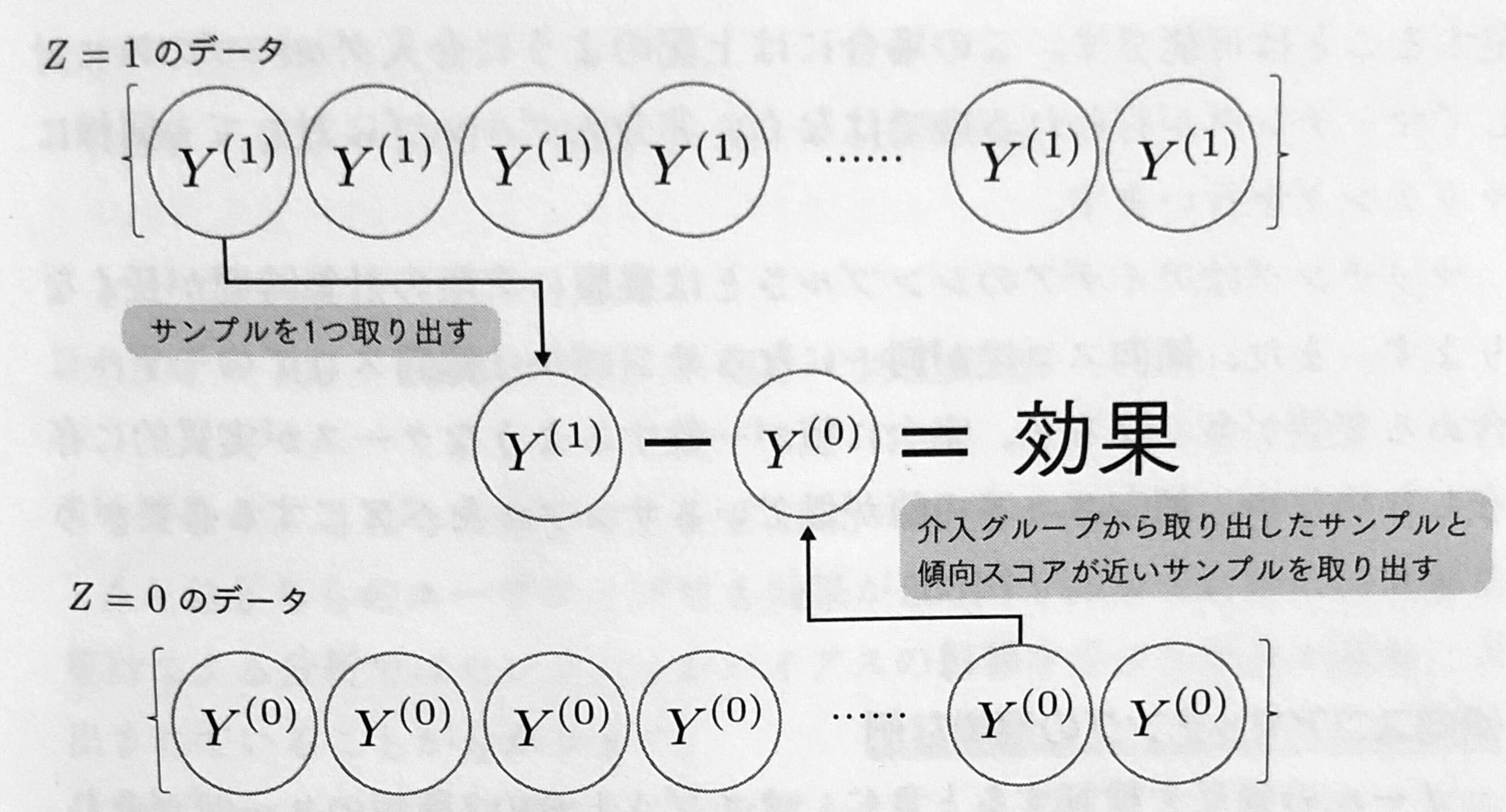
傾向スコアマッチングでは傾向スコアが近いサンプルペアを作り、効果を算出しその平均を取る。介入グループからサンプルを取り出し、非介入グループから傾向スコアが近いサンプルを取り出し、これをペアとする。ペア間でYの差を算出し、平均を取ったものを効果の推定量とする。
傾向スコアマッチングでは基本的にATT(Average Treatment effect on Treated)、つまり介入を受けたサンプルにおける効果を算出している。非介入グループに対してもマッチングを行うことでATE(Average Treatment effect)を算出することが可能である。
2.IPW(Inverse Probability Weighting:逆確率重み付き推定)
実際のデータにおいては、1つのサンプルでは $Z=1$ か $Z=0$ のどちらかの状態しか観測されない。つまり$Y^{(1)}$ は $Z=1$ となるサンプルのみにおいて観測され、$Y{(0)}$ は $Z=0$ となるサンプルのみにおいて観測される。
このデータを使って、$Y^{(1)}$と$Y^{(0)}$の平均を取ることは、$E[Y^{(1)}|Z=1]$ と $E[Y^{(0)}|Z=0]$の推定値となり、この差分を使って効果の推定を行うと、 セレクションバイアスを含む結果になってしまう。
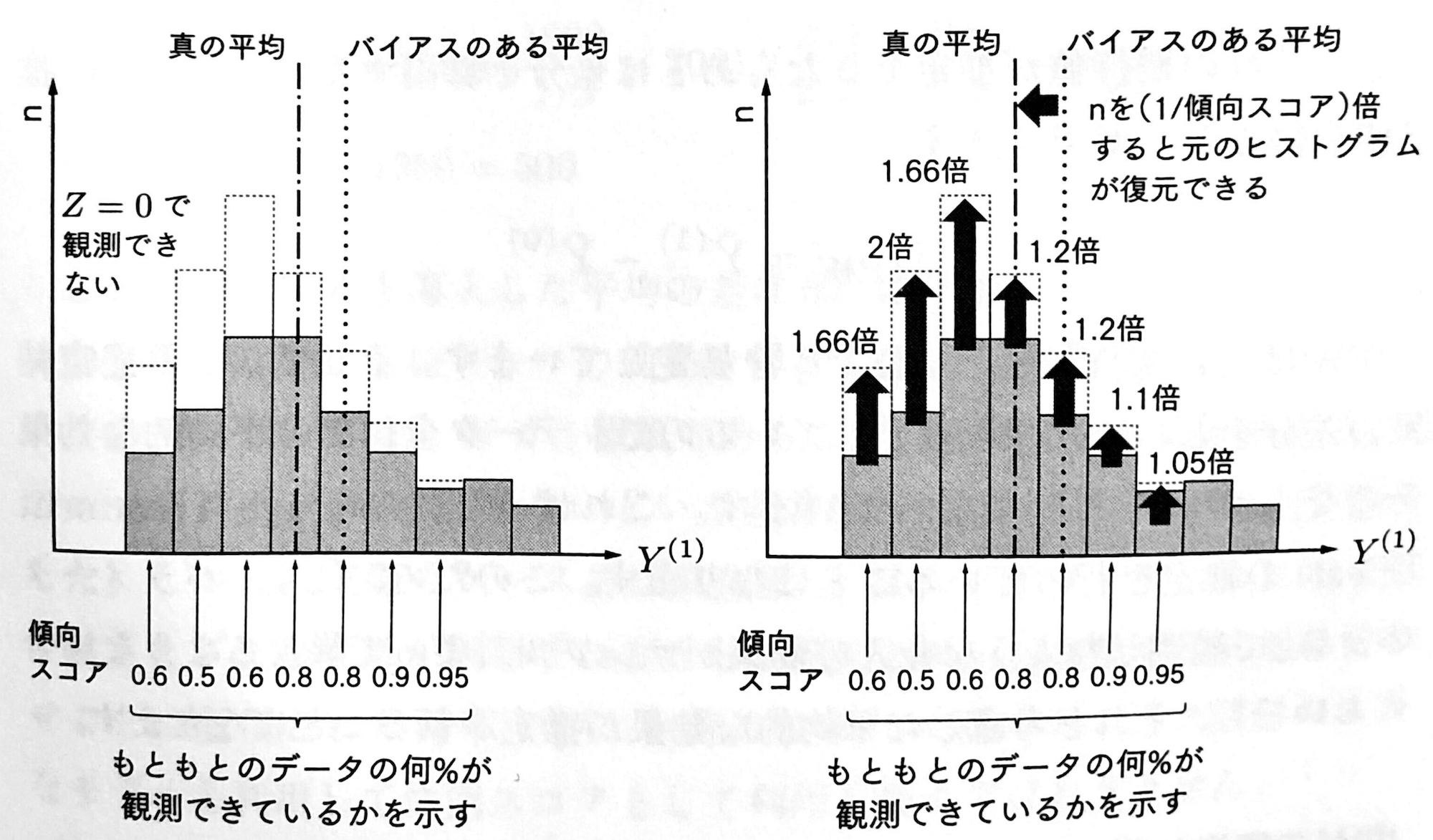
少し具体例で話すと、特徴量 $X$ を持つサンプルに関する介入が傾向スコア $P(X)$ に従って決定するという状況を想定する。仮にサンプルの $P(X) = 0.7$ となる場合、サンプルの70%は $Z=1$ として観測され、残りの30%は $Z=0$ として観測されていることになる。
つまり、$Z=1$となったサンプルは全体の中で P(X) が高い値のサンプルばかりとなり、$Z=0$ となったサンブルではデータセット全体の中で $1-P(X)$ が高い値のサンプルばかりとなっています。このとき、仮に $P(X)$ と $Y^{(1)}$ に正の相関があるとすると、$Y^{(1)}$ が小さいデータほど $Z=1$のデータには含まれないことになり、本来知りたい $E[Y^{(1)})]$よりも大きい値が推定されることになってしまう。
IPWは、傾向スコアを重みとした重み付き平均を取りその差分を取ることで、介入 / 非介入グループにおける傾向スコアの偏りに対するアイデア。介入を受けたサンプルの平均 $\bar{Y}^{(1)}$ と介入を受けなかったサンプルの平均 $\bar{Y}^{(0)}$ と効果$\hat{\tau}_{IPW}$は以下のように算出する。
\bar{Y}^{(1)}=\sum_{i=1}^{N} \frac{Z_{i} Y_{i}}{\hat{P}\left(X_{i}\right)} / \sum_{i=1}^{N} \frac{Z_{i}}{\hat{P}\left(X_{i}\right)}\\
\bar{Y}^{(0)}=\sum_{i=1}^{N} \frac{\left(1-Z_{i}\right) Y_{i}}{1-\hat{P}\left(X_{i}\right)} / \sum_{i=1}^{N} \frac{\left(1-Z_{i}\right)}{1-\hat{P}\left(X_{i}\right)}\\
\hat{\tau}_{IPW}=\bar{Y}^{(1)}-\bar{Y}^{(0)}
この数式が意味するところは、下図のように例えば $Z=1$ の平均値では本来観測されない$Z = 0$のサンプル分だけ重みを付けているということになる。
IPWでは $E[Y^{(1)}]$ と $E[Y^{(0)}]$ を推定しその差分を取ることで効果を推定しているので、 データ全体での平均的な効果ATEの推定を行っている。
傾向スコアの評価
良い傾向スコアを得るための基準としては以下が挙げられる
- データに対する説明力としてc統計量などの指標が一定値を上回っているか
- 傾向スコアによるマッチングや重み付けを行った後の共変量のバランスが取れているか
2を評価する指標として代表的なものにStandardized Differenceがあり、以下の式で算出する。この値が小さいほど、介入 / 非介入グループ間で共変量にバランスが取れていることになる。
量的変数 sd_{\mathrm{cont}}=\frac{\bar{x}_{1}-\bar{x}_{0}}{\sqrt{\left(s_{1}^{2}+s_{0}^{2}\right) / 2}}\\
2値変数 sd_{\mathrm{bin}}=\frac{\hat{p}_{1}-\hat{p}_{0}}{\sqrt{\left(\hat{p}_{1}\left(1-\hat{p}_{1}\right)+\hat{p}_{0}\left(1-\hat{p}_{0}\right)\right) / 2}}