はじめに

その性質からプログラミング入門によく使われるフィボナッチ数列。私はこのフィボナッチ数列が大好きで、プログラミングを楽しいと感じたきっかけであるとさえ思っています。
さて、個人的な話はさておき、今回はPython3でフィボナッチ数列を以下に示す3通りの方法で求めてみます。各々の求め方の話はネット上に転がっていますが、それらがまとまった解説ページは(私が探した限りでは)見つからなかったので、個人的な備忘録も兼ねて書いてみました。

一般項から求める方法
反復的な(forで回す)解法
再帰的な解法(メモ化も含む)

フィボナッチ数列の定義

フィボナッチ数列とは二つの初期条件(初項$F_0=0$, 第二項$F_1=1$)を持つ ¹ 漸化式$F_n=F_{n-1}+F_{n-2}$で表される数列です。具体的には$0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...$です。
この数列はもちろん数学的にも重要な意味を持つのですが、for構文や再帰関数の理解に最適なため、プログラミング入門で扱うのに適しています。

一般項から求める方法

フィボナッチ数列には一般項があり、それは以下の数式で表されます。

F_n=\frac{1}{\sqrt{5}}\left\{\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right\}

では、この式を使ってフィボナッチ数列の第n項を求めてみましょう。ただし、第n項のフィボナッチ数は$F_{n-1}$であることに注意しましょう。
ここでは、漸化式の計算について応用の広い代数計算モジュールであるsympyを使います。

general_term.py

import sympy as sym # sympyのインポート

def Fib(n):
    x = sym.symbols('x', nonnegative=True, integer=True)
    Fib = 1 / sym.sqrt(5) * (((1+sym.sqrt(5))/2)**(n-1) - ((1-sym.sqrt(5))/2)**(n-1))
    result = Fib.subs(x, n) # Fibの式のxにnを代入
    result = sym.simplify(result) # 式の整理
    return result

試しに$n=1,2,...,10$で計算してみます。

Fiblist = []
for n in range(1, 10):
    Fiblist += [Fib(n)]
print(Fiblist)
# [0, 1, 1, 2, 3, 5, 8, 13, 21]

実際の値と一致しているので成功してそうです。

ちなみにリスト内法表記を使うと以下のように書けます。こちらの方が簡略なので以降はこちらを使います。

print([Fib(n) for n in range(1, 10)])
# [0, 1, 1, 2, 3, 5, 8, 13, 21]

プログラミングのロジックとしてはこの数値計算をするだけの方法が最も簡単です。裏を返せばプログラミング入門には向かないということですが。

一般項の求解

sympyには漸化式（階差方程式）の解を求めることができる機能があるので、もし一般項の式を知らなくても導出してしまえばよいのです。

import sympy as sym
f = sym.simplify("f(n)") #求める解
s = sym.simplify("f(n)-f(n-1)-f(n-2)") # 漸化式(s=0となるように記述する)
ini = sym.simplify({"f(0)": 0, "f(1)": 1}) # 初期条件({0:0,1:1}としても良い)
Fib_general_term = sym.rsolve(s, f, ini) # 初期条件iniの漸化式sをfについて解く

print(Fib_general_term)
# sqrt(5)*(1/2 + sqrt(5)/2)**n/5 - sqrt(5)*(-sqrt(5)/2 + 1/2)**n/5

このように一般項の求解ができます。

反復的な(forで回す)解法

これがプログラミング入門としてフィボナッチ数列を扱う際の最もオーソドックスな解法でしょう。
私たちが「n番目のフィボナッチ数列を求めて」と言われて暗算する時も大抵はこの方法を使うと思います。
Python3では以下のように書くことができます。

repetition.py

def Fib(n):
    a, b = 0, 1
    if n == 1:
        return a
    elif n == 2:
        return b
    else:
        for i in range(n-2):
            a, b = b, a + b
        return b

出力を確認してみましょう。

print([Fib(n) for n in range(1, 10)])
# [0, 1, 1, 2, 3, 5, 8, 13, 21]

引数をとる自作関数が含まれ、if文やfor文の理解が不可欠なこのコードはやはりプログラミング入門に最適でしょう。

再帰的な解法

そもそもフィボナッチ数列は漸化式で再帰的に定義されているので、最も可読性の高いコードを書くことができるのはこの解法だと思います。
Pythonの基礎文法を学んだあとに少し発展的な内容として再帰関数を学ぶのに最適な解法です。

recursion.py

def Fib(n):    
    if n == 1:
        return 0
    elif n == 2:
        return 1
    else:
        return Fib(n-1) + Fib(n-2)

初期条件2つと漸化式を記述するだけなので(慣れれば)簡単です。
出力を確認してみます。

print([Fib(n) for n in range(1, 10)])
# [0, 1, 1, 2, 3, 5, 8, 13, 21]

それぞれの方法の演算速度

方法によって演算速度が異なります。それらを比較してみましょう。
演算速度はtimeモジュールを使うことで以下のように調べられます。

import time

start = time.time()
hoge() # 速度を調べたい処理
end = time.time()
print(f'処理にかかった時間は{end - start}秒です。')

前述した3通りの方法²でn回Fib(40)を計算して平均値を出します。
用いるコードは以下の通りです。

import time

n = 10 # 再帰法以外ではn=1000とする(処理時間が短くうまく計測できないため)

start = time.time()
for i in range(n):
    Fib(40)
end = time.time()

print(f'処理にかかった平均時間は{(end-start)/n}秒です。')

結果を以下の表にまとめました。

方法	処理にかかった平均時間(秒)
一般項を用いる解法	1.228e-03
反復的な解法	1.995e-06
再帰的な解法	24.52

環境によって速度は異なるのでこの値は絶対ではありませんが、重要なのはそれぞれの方法の相対的な処理時間です。
表を見ると再帰法が圧倒的に遅いことが分かります。

再帰法は何故遅い？

再帰法が遅い理由は端的に言うと「演算回数が多いから」です。この図をみてください。

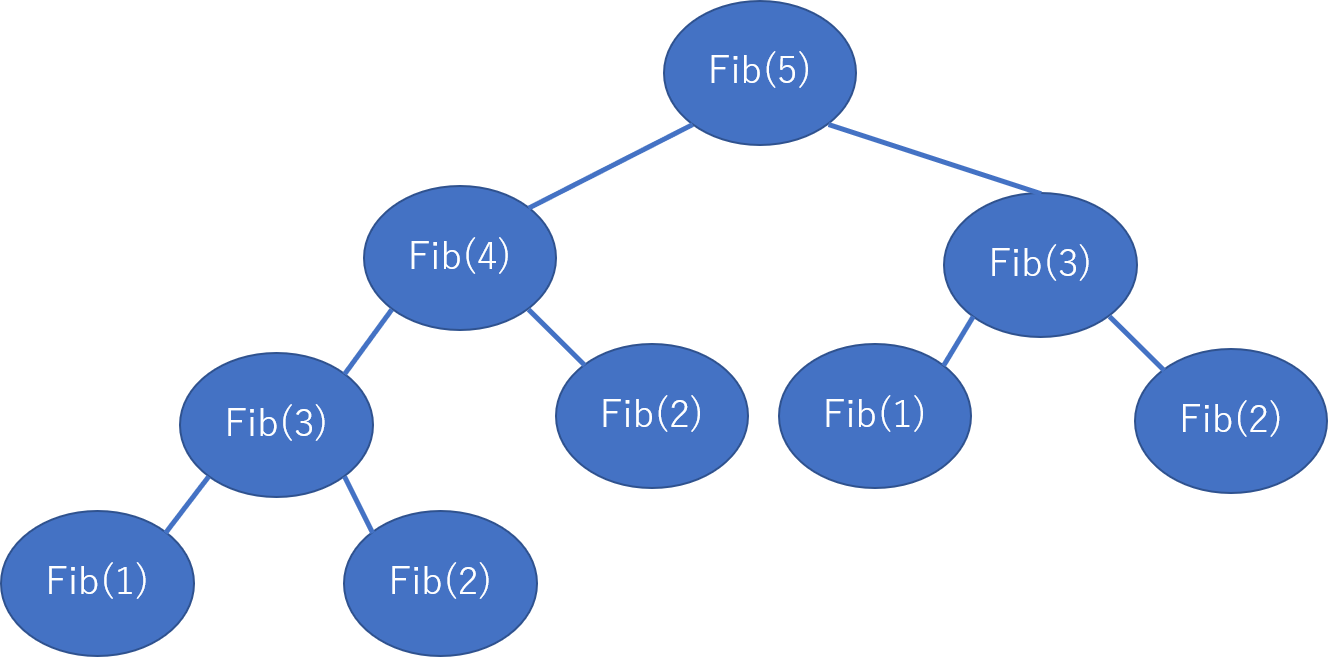
これは再帰法によるFib(5)の演算の概念図です。Fib(n)のnが大きくなると爆発的な勢いで演算回数が多くなります。

では他の方法はどうなのでしょうか。それぞれの方法のnに応じた演算回数の特徴を表にまとめました。

方法	演算回数の特徴
一般項を用いる解法	(内容は複雑だが)どんなnに対しても1回
反復的な解法	nに応じて演算回数が線形的に増加する
再帰的な解法	nに応じて演算回数が指数関数的に増加する

この特徴から、反復法より一般項の方が速いんじゃないかと思う人がいると思いますが、一般項の計算に用いている方法は全く最適化していないので反復法より遅いです(Fib(10000)でも試してみましたが、それでも反復法の方が5倍くらい速いです)。誰か最適化の方法を知っている人は教えてください。

さて、反復法は速く、再帰法は遅いというのが分かりました。でも再帰法は「あること」をすることで反復法並み、もしくはそれ以上の速さを手に入れることができます。それはメモ化です。

メモ化

再帰法はさきほど概念図に示した通り、何度も同じ関数を呼び出しています。その呼び出しのたびに演算をするため、処理が遅いのです。この問題を解決するのが「メモ化」です。

メモ化の理念

一度呼び出した関数を再び使う時に再演算しなくて済むように、一度呼び出した関数の戻り値をメモに保存しておいて、2回目以降呼び出されたときはメモに書かれた値を使う、というのがメモ化の理念です。
例えば、先ほど示した概念図をみて分かる通りFib(4)は4回、Fib(5)は8回関数を呼び出します。そのため、メモ化無しだとFib(6)を計算するのに12回関数を呼び出す必要があります。しかし、Fib(5)はすでに求めたFib(4)をわざわざもう一回求めなおしています。このFib(4)の戻り値をメモに保存して以降はそれを使うようにすると、Fib(6)は9回の呼び出しで済みます(Fib(3)もメモ化することで8回となります)。

メモ化の実装

関数が呼び出されたらメモに既にその関数の戻り値が保存されてないかを確認し、保存されていたらメモの値を返し、保存されていなかったらメモにその戻り値を書き込む。これがメモ化の根幹のアルゴリズムです。

実装例1

Pythonで再帰フィボナッチのメモ化で見た方法です。空リストと入れ子構造になったdefを使ってメモ化を実現しています。参照記事のコードを本記事の他コードと整合するように少し書き換えたものがこちらです。

recursion_memo1.py

def fib_memo(n):
    memo = ["EMPTY"] * (n+1)
    def _fib(n):
        if n == 1:
            return 0
        elif n == 2:
            return 1
        elif memo[n] != "EMPTY":
            return memo[n]
        else:
            memo[n] = _fib(n-1) + _fib(n-2)
            return memo[n]
    return _fib(n)

10000回Fib(40)を計算して平均値をとると、その平均処理速度は1.999e-05秒でした。単純な再帰法よりかなり速くなっています(構造が複雑な分、反復法よりは劣りますが)。

実装例2

辞書型を使う方法もあります。また、defを入れ子にせずとも、2つ引数を持つ関数にすればメモを保持できます。この方法は事前にメモがあればそれを使えるというメリットがあります。

recursion_memo2.py

def Fib(n, memo={}):
    if n == 1:
        return 0
    elif n == 2:
        return 1
    elif n in memo:
        return memo[n]
    else:
        memo[n] = Fib(n-1, memo) + Fib(n-2, memo)
        return memo[n]

同様に10000回Fib(40)を計算して平均値をとると、その平均処理速度は1.998e-07秒でした。
実装例1より単純な(速く計算できる)構造なため、反復法より速く演算できています。

実装例3

Pythonにはfunctoolsモジュールという高階関数用のモジュールがあり、それを使えば非常に簡単にメモ化が実装できます。ただ、ブラックボックスなのでメモ化のアルゴリズムの勉強にはなりません(モジュールのソースコードを読める人なら別ですが)。

recursion_memo3.py

from functools import lru_cache

@lru_cache(maxsize=None)
def Fib(n):
    if n == 1:
        return 0
    elif n == 2:
        return 1
    else:
        return Fib(n-1) + Fib(n-2)

同様に10000回Fib(40)を計算して平均値をとると、その平均処理速度は1.199e-07秒でした。
どの実装例よりも速く演算できています。実用的にはこの方法が最適でしょう。

補足:行列を使ったフィボナッチ数列の求め方

とある2*2行列のべき乗を使うとフィボナッチ数列を計算することができます。それには自然数nについて成り立つ以下の定理を用います。

A = \left(\begin{array}{rrr}1 & 1  \\1 & 0\end{array}\right)においてA^{n-1}の1行1列要素はF_nと等しい

これを用いてフィボナッチ数列を求めるプログラムをsympyで実装しましょう。ただし、第n項のフィボナッチ数は$F_{n-1}$であることに注意しましょう。

array.py

import sympy as sym

def Fib(n):
    if n == 1:
        return 0
    else:
        A = sym.Matrix([[1, 1],
                        [1, 0]])
        FibArray = A ** (n-2)
        return FibArray[0, 0]

#試しに計算してみる
print([Fib(n) for n in range(1, 10)])
# [0, 1, 1, 2, 3, 5, 8, 13, 21]

10000回Fib(40)を計算して平均値をとると、その平均処理速度は1.699e-04秒でした。反復法に一歩及ばないといったところでしょうか。逐次平方というメモ化に似たテクニックを使えばもっと速くなると思います。

おわりに

この記事ではPythonでフィボナッチ数列を求める色々な方法をまとめて紹介しました。フィボナッチ数列の面白さやプログラミングの楽しさが共有できたならば幸いです。
個人的な話をすると、この記事が私の初投稿なのですが、Markdown記法に慣れず、調べながら書いたので思ったより時間がかかってしまいました。
誤字脱字や誤った記述、更に良いアルゴリズム、気づいたこと、感想などがあればぜひコメントをください。

記事中に示したもの以外の参考文献

フィボナッチ数 - Wikipedia
sympyで「フィボナッチ数(Fibonacci number)」の一般項を出力してみた
 1.2.4 べき乗 - SCIP
フィボナッチ数列の任意の項を高速に計算する方法
 問題解決のPythonプログラミング

初項を1, 第二項を1とする場合もあるようですが、この記事では初項0, 第二項1で統一しています。 ↩
一般項の方法はgeneral_term_improved.pyの方を使います。 ↩

Pythonによるフィボナッチ数列の色々な求め方(一般項、反復法、再帰法)