More than 3 years have passed since last update.

LAPRASAdvent Calendar 2019

@donaldchi(池光龍)in

LAPRAS株式会社

Echo State Networkの詳細を解説してみる

Last updated at 2019-12-27Posted at 2019-12-25

前書き

**リザーバーコンピューティング(Reservoir Computing, 以降RC)**と言う種類のニューラルネットワークがあります。

RCは系列データを有効且つ高速に学習するためのアーキテクチャーを提供していて、データ量が少ない状況あるいは限られた資源(資金、計算能力)の元で系列データ処理モデルを構築したい場合、力を発揮しています。

今回はRCの代表的なモデルであるEcho State Network(ESN)を解説してみることで、ESN, RCに対する理解を深めて行きたいです。

ESNに関する記事は検索かけると沢山出てはいますが、今回は自分が調べたものの振り返りの意味も含め記事化します。

RNNとの違いから

系列データ学習で有効なモデルとして、RNNが知られています。RNNは過去のコンテキスト情報を記憶して置いて、新規入力が来た時に過去情報も共に考慮した処理を行う仕組みで前後の入力に相関のある系列データの学習に成功しています。

RCもRNNと同じく過去の情報を扱っています。しかし、違いとして、RNNは学習された重みで過去の情報を受け取る反面、RCは学習されていない重み(ランダム重み)で過去の情報を受け取っています。

まだ、学習に置いて、RNNは入力、過去情報の伝搬(マルコフ性抽出)、出力全般に置いて重み学習を行わなければならない反面、RCは入力、過去情報の伝搬(マルコフ性抽出)部分は固定されたランダム重みで計算を行い、出力の重みのみをタスクに最適な出力をだすように学習するため、非常に低い計算コストでモデルを構築することができます。

さらに、出力部分重みのみの学習になるため、入力、過去情報の伝搬部分はいろんなタスクで共通で使うことができます。

それではRC系モデルの構造を見ていきます。

RC系モデルの構造をみる

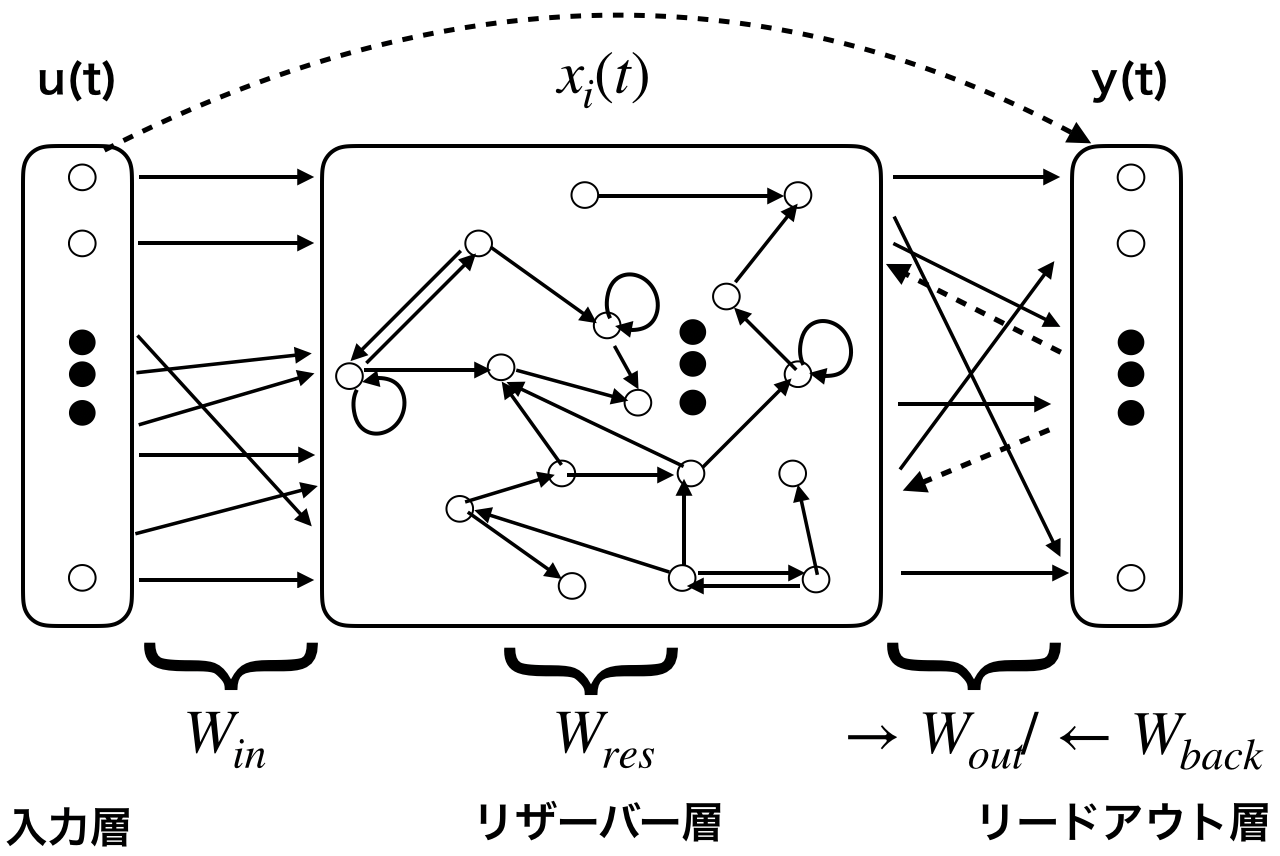
スクリーンショット 2019-12-24 14.17.13.png (217.7 kB)

各記号の定義と説明:

K : 入力データの次元
N : リザーバー層内のニューロン数; $K \ll N$
L : 出力データの次元
$u(t)$ : 時刻tでの入力データ; 次元: $(K, 1)$
$x_i(t) \in X(t)$ : 時刻tでのニューロン i の状態; 次元: $(1, N)$
$X(t)$ : 時刻tでリザーバー層のニューロン達が持つ状態; 次元: $(N, N)$
$y(t)$ : 時刻tでの出力データ; 次元: $(L, 1)$
$W_{in}$ : 入力層重み; 次元: $(K, N)$
$W_{res}$ : リザーバー層の重み; 次元: $(N, N)$
$W_{out}$ : 出力層重み; 次元: $(N, L)$
$W_{back}$ : 出力からのフィードバック重み; $(L, N)$
$f(x)$ : リザーバー層の活性化関数; 一般的にtanh, sigmoidを使う
$g(x)$ : 出力層の活性化関数; 一般的に恒等関数、sigmoidを使う

RC系モデルは、主に入力層(Input)、リザーバー層(Reservoir)、リードアウト層(Readout)三層からなります。

入力層からの情報はランダム値で初期化された重み($W_{in}$)によって変換され、リザーバー層の各ニューロンに渡されます。

リザーバー層はN個のニューロンがスパースでランダムに連結された再帰的なネットワークで構成されます。

各ニューロンはそれぞれ自分の状態$x_i(t)$を持っていて、この状態は現時刻tでの入力: $u(t)$と過去から得られた情報: $x_i(t-1)$、出力からのフィードバック: $y(t-1)$によって更新されます。

ニューロンの状態更新式

$x(t) = f(W_{in}u(t) + W_{res}x(t-1) + W_{back}y(t-1))$

リードアウト層は、リザーバー層のニューロンが持つ状態($X(t)$)と入力データ($u(t)$)を使って、出力の予測を行います。

出力
$z(t) = [X(t); u(t)]$
$y(t) = g(W_{out} z(t))$

z(t)は入力$u(t)$とニューロン状態$X(t)$の連結をさします。

ここまで、RC系モデルの大体の構造を説明しましたが、実は以下のような観点からRC系モデルには大量の変形が存在します。

入力ドリブン vs 入力とフィードバックドリブン
- 上では入力とフィードバック両方の情報を使ってリザーバー層の状態更新を行っていました。これはあくまで入力だけでは検知できないパターンが存在するタスクに限る話でそうでない場合はフィードバック情報を無視しても大丈夫です。

例えば、信号発声器の場合入力だけでは振動情報の学習ができないため、フィードバックもリザーバー層に入力させる
from http://www.scholarpedia.org/article/Echo_state_network

ニューロンモデルの種類
出力の計算でニューロン状態以外に入力データを使うかいなか
出力で使うモデル
- 上の説明では、MLPを想定した説明していますが、実は出力モデルとして色んなモデルが使えます。例えば、MLP, SVM, kNNなど。
出力が一つか複数あるか
- タスクによって変わるのは、出力部分の重み($W_{out}$)だけなので、同じリザーバーを使って同時に複数のタスクを解くことも考えられます。

Echo State Network (ESN)を理解する

Echo State Network(ESN) はRCの代表的なモデルの一つで上図のような構造をとっています。

ESNがうまく行く理由の一つ

ESNは入力データを低次元($K次元$)から高次元ニューロン状態空間($NxN$)へ非線型変換で写像することで、入力の線形分離を可能にします。これはカーネル法の発想と同じで、ESNの学習がうまくいく理由の一つとして挙げられます。

Echo state propertyについて

ESNのリザーバー層は非線型関数ニューロンモデルで表現されたニューロンの再帰的ネットワークで構成されています。ニューロン間連結の仕方と重みはランダムに決められるものの、過去の情報を持つニューロンの状態により、時系列パータンが学習されるようになります。

しかし、ESNは過去の記憶が時間によって消失していくという制限(Echo state property) をかけることで、短期な記憶情報のみを活かしています。

モデルがEcho state propertyを持つことにより、

ニューロンの状態がリザーバーへの入力データに漸近的に依存する
初期状態の影響が徐々になくなる

ということが起きます。

あくまで個人的な考えですが、ESNは短期で消失していく記憶を扱うコンセプトをとることで、ニューロン間のランダム結合による悪影響を一定水準に抑えめているのではないかと思います。
(ここはあとで調べたいし、まだ実験して見たいと思います。)

モデルにEcho state propertyを与えるためには、

条件: $w_{res}$のスペクトル半径(spectral radius) $\rho(W_{res}) < 1$

を満たす必要があります。これはこの条件の元で $\lim_{n\rightarrow \infty} \mathrm {W_{res}}^{n} = 0$になるため(from スペクトル半径)、ニューロンの状態が$W_{res}$をどんどんかけて更新して行くにつれ、過去の情報が消失して行くからです。

実際にプログラミングをするとき、$W_{res}$の決め方の一つとして、以下の式が使われたりします。

$W_{res} = W_{random} \frac{\rho_{desired}}{\rho(W_{random})}$

ESNの学習について

ESNはパラメーター$W_{out}$を求めるために、offline trainingでは最小二乗法を、online traningでは再帰的最小二乗法を使います。

offline trainingの場合はより有効な学習を行うためにパラメーター更新式に正則化項を与えています。
$W_{out} = Y_{target} X^T(XX^T + \lambda_rI))^{-1}$　($\lambda_r$ : 正則化係数)

出力フィードバックを受けるモデルの場合、モデルの安定化に寄与するという理由から、ニューロン状態更新式に一定のノイズを与える処理も行ったりします。(from : Echo state network)

ノイズを入れたニューロン状態更新式
$x(t) = f(W_{in}u(t) + W_{res}x(t-1) + W_{back}y(t-1)) + v(n)$　($v(n)$ : ノイズ)

$W_{res}$のスペクトル半径の場合、$\rho(W_{res})$値が大きければ大きいほど、記憶消失の速度が遅くなり、ニューロンがより長い記憶まで持つことになります。更に、リザーバー層で線形変換による状態更新が行われる場合、最長の記憶を持つことになり、$N$ステップ前の記憶まで保存されます。

リザーバー層内のニューロンの結合について、リザーバー層内で生成されるニューロン状態の多様性を保つため、ニューロン達はスパース且つランダムに結合されるべきだとモデル提案初期では主張されましたが、全結合のネットワークでも普通に性能がでることがわかっています。なので、スパース且つランダム結合のメリットとしては、計算量が減る以外のメリットはないらしいです。

似たようなアプローチ

Liquid State Machine (LSM)

Liquid State Machine(LSM)はESNとほぼ同時期に提案されたもう一つの代表的なRC系モデルです。LSMも構造上はESNと同じですが、ちょっと変わったニューラルネットワーク Reservoir Computingでも言及したように、生体模倣に充実度が高い、ニューロンの活動電位を表現したニューロンモデルを採用しています。

まだ、Fading MemoryというESNのEcho state propertyと似たようなコンセプトにより、過去一定期間内の記憶を時間によって消失する形で持つということを実現しています。

Weight Agnostic Neural Networks(WANN)

NeurIPS 2019で発表されたWeight Agnostic Neural Networksは元となる仮説が似ている印象だったので記載します。

WANNは

実際の生物を観察すると, 生まれたてにも関わらずに運動能力や認知能力をすぐに獲得する。NNs で言えばパラメータがまだランダムな状態でもある程度の能力が獲得できるということになる。

(from http://cympfh.cc/paper/weightanogstic.html)
と言う仮説を元に重み学習(ランダム重み)をしなくても特定能力(例えば、蛇は生まれた時から天敵を識別し、逃げるという能力を持つ。)を模擬できるネットワークを探すと言うアプローチを提案しています。

一方、ESN / LSMは生まれたてた状態(ランダム重み)からすぐに特定能力を獲得することを出力重みのみを学習することで実現しています。

まとめ

今回はESNについて調べた結果をちゃんと理解するために記事化しました。自分の理解度と調べた範囲の限界で間違ったことも書いてあるかもしれないので、ご指摘頂けると嬉しいです。

参照文献

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up