JuliaでDeep Learningを理解する: 3.3 Shallow network regions

Understanding Deep LearningのノートブックをJuliaで確認する。

3.3 Shallow network regions

JuliaでDeep Learningを理解する: 3.2 Shallow neural networks IIで活性化関数が領域を分割することを確認した。領域数はxの次元数Diと隠れユニットの数Dに依存する。その数はZaslavsky式で与えられる。

\begin{equation}N = \sum_{j=0}^{D_{i}}\binom{D}{j}=\sum_{j=0}^{D_{i}} \frac{D!}{(D-j)!j!} \end{equation}

Juliaで書くと

number_regions(Di, D) = sum([binomial(big(D), j) for j in 0:Di])

Int64の範囲を超えるのでbig(D)でBigInt型にしている。

inputdims = [1, 5, 10, 50, 100]
hiddenunits = 1:1000
fig = Figure()
ax = Axis(
    fig[1, 1],
    xlabel="隠れユニットの数",
    ylabel="領域の数",
    ytickformat=values -> rich.("10", superscript.(string.(Int.(values))))
)
for inputdim in inputdims |> reverse
    regions = log10.(number_regions.(inputdim, hiddenunits))
    lines!(ax, hiddenunits, regions, label="Dᵢ=$inputdim")
end
axislegend()

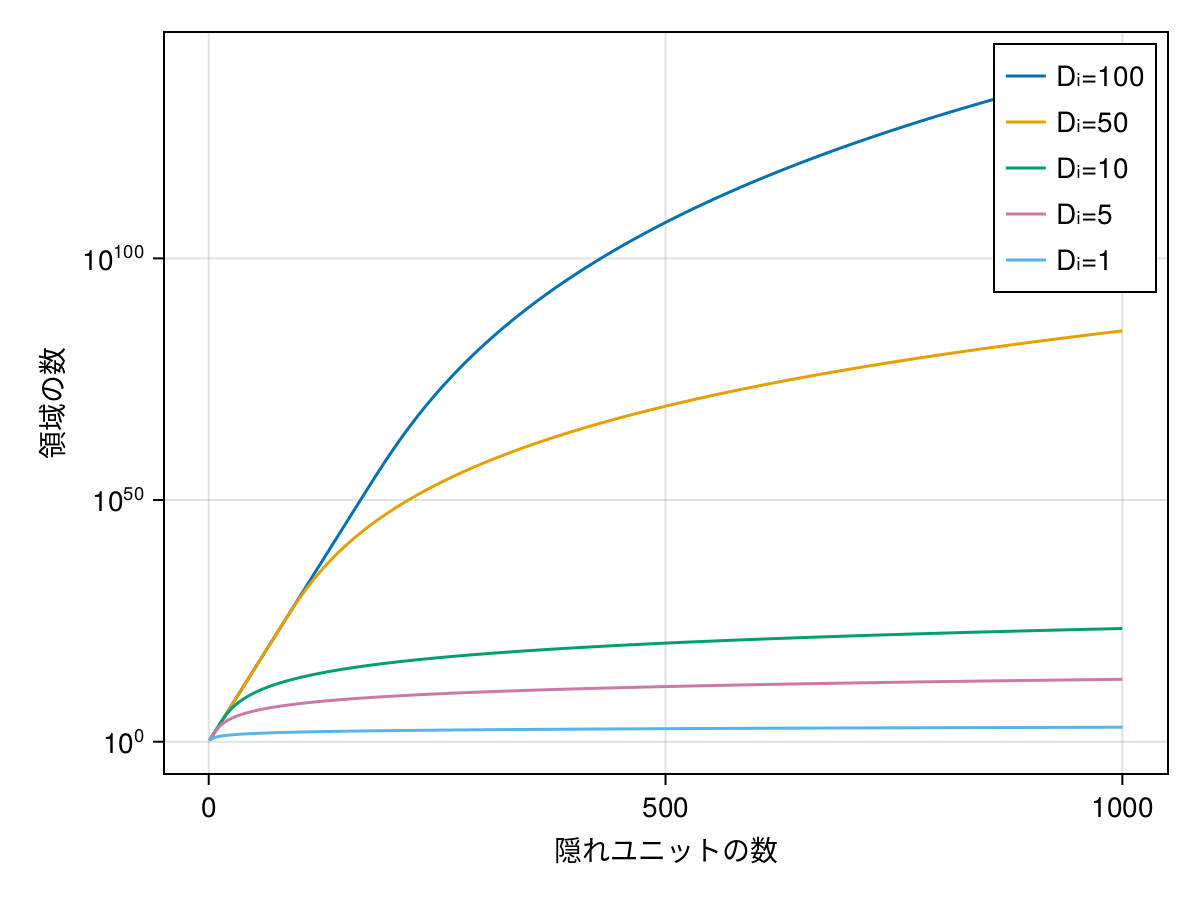
縦軸はlogスケールなので、急激に領域数が大きくなっていることがわかる。そして隠れユニット数より入力次元に強く依存する。これは次元の呪いとも関係がある。