AmazonBraketで学ぶ量子コンピュータ③

この記事について

量子コンピュータの勉強をはじめて最近一通りAmazonBraketを触り終えました。
最近登場したサービスであることもあり、少し丁寧なドキュメントを残しておくと後続の方が勉強しやすくなったり、参照してわからないところを調べる際に便利かなと思ったので
自分自身の理解向上も兼ねて記事にまとめていっています。

また、量子コンピュータ関係の他の記事は、下記で紹介しています。

※本記事は2021年2月に更新している記事です。更新などにより内容が変わっている可能性もあるのでご注意ください。

概要

本記事では量子コンピュータの導入部分に関して解説をしていこうと思います。
参照するのはこちらの2_Running_quantum_circuits_on_QPU_devices.ipynbというサンプルです。
こちらのサンプルではAmazonBraketで学ぶ量子コンピュータ①で紹介したよりも少しだけ応用的な内容が記載されています。
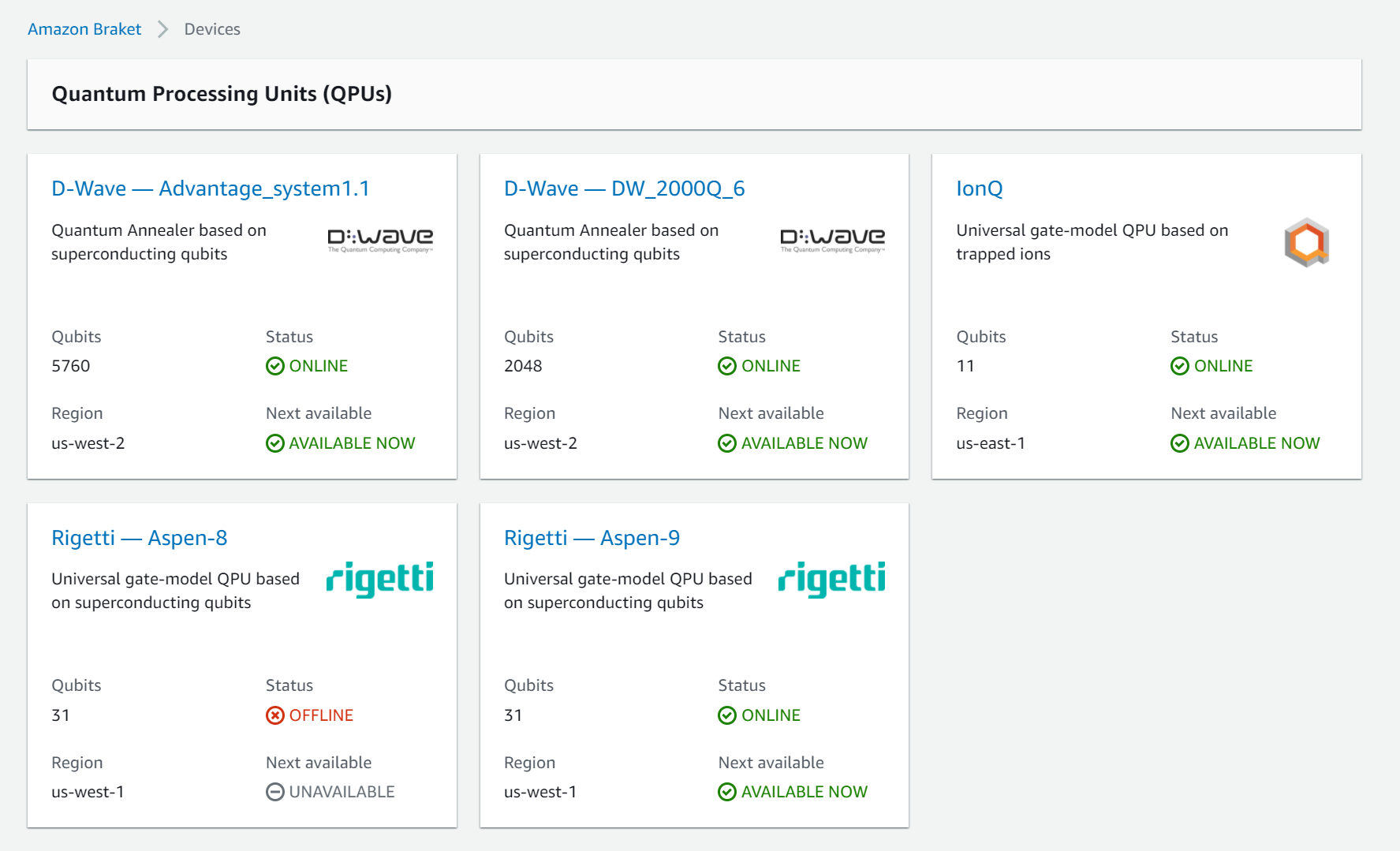
具体的には、以下に示される実機を実際に使ってみて量子回路の挙動を確かめてみよう！といったような内容になっています。
特に今回はIonQとRigetti-Aspen-8を対象としています。

前提知識

まず簡単に今回扱うサンプルを理解するために必要な量子コンピュータ（ゲート型）を扱うのに必要な前提知識を説明していきます。
とは言っても今まで扱ってきたサンプル解説から逸脱することはないので、はじめての方はAmazonBraketで学ぶ量子コンピュータ①という導入部分を説明している記事もありますのでそちらから読むのも良いかと思います。
何もないのも寂しいので本記事でも簡単に上記記事の内容を振り返ります。

量子ビットの表現

量子ビットは2次元複素ベクトル空間での正規直交基底として各ビットを表現します。
それぞれのビットはディラックによって考案されたケット表記を用いて以下のように表現されます。

|0 \rangle =\begin{pmatrix} 1 \\ 0 \end{pmatrix}, \ \ \ \ \  |1 \rangle =\begin{pmatrix} 0 \\ 1 \end{pmatrix}

重ね合わせ

特に、量子力学では「重ね合わせ」という特有の概念があります。
これは任意の量子状態を重み情報と位相情報が含まれた複素数 $\alpha, \beta$を用いて、以下のように表現できます。

|x\rangle = \alpha |0\rangle + \beta |1 \rangle = \alpha \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \beta \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} \alpha \\ \beta \end{pmatrix}

$|0 \rangle$ 状態は複素数の確率振幅$\alpha$ をもち、観測確率が $|\alpha|^2$で、$|1 \rangle$ 状態は確率振幅 $\beta$を持ち観測確率が $|\beta|^2$であることを示しており、以下のように規格化されています。

|\alpha|^2 + |\beta|^2 = 1

量子ゲート操作

量子ビットの操作は行列計算を用いた量子ゲート操作により実現されます。
例えば、何かしらの操作を行うことで $|0\rangle$が $|1\rangle$に変更され、$|1\rangle$ が $|0\rangle$に変更されるような回路$X$は以下のように定義されます。

X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}

上記、Xゲートは1量子ビットの反転操作を行うため、反転ゲートとも呼ばれます。

他にも1量子ビット操作では、位相・ビット反転ゲートのYゲートや位相反転ゲートのZゲート等が存在します。
以下のアダマールゲートを用いることで重ね合わせ状態を作ることができるのでそれも覚えておくと良いかと思います。

H = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}

2量子ビットの表記方法

2量子ビットは以下のように表すことができます。

\begin{split}\begin{equation}\begin{split}
    \left|{00}\right\rangle &= \begin{pmatrix}
        1 \begin{pmatrix}
            1  \\
            0
        \end{pmatrix} \\
        0 \begin{pmatrix}
            1  \\
            0
        \end{pmatrix}
    \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \\0 \end{pmatrix}~~~\left|{01}\right\rangle = \begin{pmatrix}
    1 \begin{pmatrix}
    0 \\
    1
    \end{pmatrix} \\
    0 \begin{pmatrix}
    0  \\
    1
    \end{pmatrix}
    \end{pmatrix} = \begin{pmatrix}0 \\ 1 \\ 0 \\ 0 \end{pmatrix}\end{split}
\end{equation}\end{split}

\begin{split}\begin{equation}\begin{split}\left|{10}\right\rangle = \begin{pmatrix}
    0\begin{pmatrix}
    1  \\
    0
    \end{pmatrix} \\
    1\begin{pmatrix}
    1 \\
    0
    \end{pmatrix}
    \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}
   \left|{11}\right\rangle = \begin{pmatrix}
    0 \begin{pmatrix}
    0  \\
    1
    \end{pmatrix} \\
    1\begin{pmatrix}
    0  \\
    1
    \end{pmatrix}
    \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\1 \end{pmatrix}\end{split}
\end{equation}.\end{split}

なのでベクトルのそれぞれの成分が以下のように対応していることがわかると思います。

\begin{pmatrix} |{00}\rangle \\ |{01}\rangle \\ |{10}\rangle \\ |{11}\rangle \end{pmatrix}

2量子ビットの操作

2量子ビットの操作で最も有名なものの一つがCNOTゲート（制御NOTゲート）でした。
これは0量子ビット目が$|1 \rangle $ の時に 1量子ビット目のビットを反転させる操作を行います。
具体的には、

CNOT =
\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 1\\
0 & 0 & 1 & 0
\end{pmatrix}

と示されます。

AmazonBraket

ここから実際にAmazonBraketを使って説明していきます。
環境を用意されていない方は、まずはこちらの記事やドキュメントなどを参考に環境を用意してください。

環境を用意すると以下のようにデフォルトでサンプルコードがGitHubからインポートされています。

今回はこの配下にある
getting_started/2_Running_quantum_circuits_on_QPU_devices.ipynb
を見ていきます。

事前準備

import

importにおいては特に特別なものは必要なく、量子にかんしては以下の通りのモジュールをインポートするだけで充分です。

# AWS imports: Import Braket SDK modules
from braket.circuits import Circuit, Gate, Observable
from braket.devices import LocalSimulator
from braket.aws import AwsDevice

S3バケットの登録

ローカルシミュレータ以外はS3に取得結果の情報を格納する動きになっています。
そのため、S3にバケットを用意してあげて、以下の変数に値を格納しておいてください。

# Enter the S3 bucket you created during onboarding in the code below
my_bucket = "amazon-braket-Your-Bucket-Name" # the name of the bucket
my_prefix = "Your-Folder-Name" # the name of the folder in the bucket
s3_folder = (my_bucket, my_prefix)

本体

実機で利用できる回路群

Amazon Braket では実機で使える回路群の確認を行うことができます。
応用的な回路を組む際、実機によって利用できる回路が異なるので一部の実機に関してはアルゴリズムなどに合わせて自ら回路を作成していく必要があることを意味します。
次のコードは

• SDK
• Rigetti-Aspen8
• IonQ

のそれぞれで使える回路群を示します。

# print all (the usual suspects) available gates currently available within SDK
gate_set = [attr for attr in dir(Gate) if attr[0] in string.ascii_uppercase]
print('Gate set supported by SDK:\n', gate_set)
print('\n') 

# the Rigetti device
device = AwsDevice("arn:aws:braket:::device/qpu/rigetti/Aspen-8")
supported_gates = device.properties.action['braket.ir.jaqcd.program'].supportedOperations
# print the supported gate set
print('Gate set supported by the Rigetti device:\n', supported_gates)
print('\n') 

# the IonQ device
device = AwsDevice("arn:aws:braket:::device/qpu/ionq/ionQdevice")
supported_gates = device.properties.action['braket.ir.jaqcd.program'].supportedOperations
# print the supported gate set
print('Gate set supported by the IonQ device:\n', supported_gates)

これを実行すると以下のような結果が返ってきます。

Gate set supported by SDK:
 ['CCNot', 'CNot', 'CPhaseShift', 'CPhaseShift00', 'CPhaseShift01', 'CPhaseShift10', 'CSwap', 'CY', 'CZ', 'H', 'I', 'ISwap', 'PSwap', 'PhaseShift', 'Rx', 'Ry', 'Rz', 'S', 'Si', 'Swap', 'T', 'Ti', 'Unitary', 'V', 'Vi', 'X', 'XX', 'XY', 'Y', 'YY', 'Z', 'ZZ']


Gate set supported by the Rigetti device:
 ['cz', 'xy', 'ccnot', 'cnot', 'cphaseshift', 'cphaseshift00', 'cphaseshift01', 'cphaseshift10', 'cswap', 'h', 'i', 'iswap', 'phaseshift', 'pswap', 'rx', 'ry', 'rz', 's', 'si', 'swap', 't', 'ti', 'x', 'y', 'z']


Gate set supported by the IonQ device:
 ['x', 'y', 'z', 'rx', 'ry', 'rz', 'h', 'cnot', 's', 'si', 't', 'ti', 'v', 'vi', 'xx', 'yy', 'zz', 'swap', 'i']

全部は説明しませんが、いくつかのポイントを押さえておきます。

	X, Y, Z, H, I, S, T	CNOT(CX), CY, CZ	Rx, Ry, Rz	XX, YY, ZZ	swap
SDK	○	○	○	○	○
Aspen-8	○	○	○	×	○
IonQ	○	○	○	○	○

上記よりほとんど基本的な回路が表現可能だということがわかりますが、
Aspen-8のみXX, YY, ZZ回路を表現できません。
例えば、ZZ回路は CNOT、CZ、CNOTを用いて表されるので自分で回路を作ってあげる必要があります。
とくにQAOAのような最適化アルゴリズムに用いる場合はZZ回路が必要とされるので注意が必要です。

他にもアルゴリズムに応じてデフォルトで回路が実装されていない場合がありますのでこちらのコードを実行してみて確認してみてください。

ベル状態の準備

次にベル状態を準備して、ローカルシミュレータで実行してみます。
Amazon Braketのサンプル上ではちょうど続きに位置しているので続けて実行していただければよろしいですが、
AmazonBraketで学ぶ量子コンピュータ①で紹介させていただいた内容とかぶっているため割愛させていただきます。
詳細を見てみたい方は上記を参考にしてみてください。
また、ローカルシミュレータは

低〜中程度のqubit数(𝑁<20-25)の高速実験に適しており、回路の深さは無制限である。

とのことです。
もちろん回路の深さを深くすると時間がかかりますし、qubitが多くても時間がかかるので注意してください。

Aspen-8（実機）での実行

Rigetti社の用意しているAspen-8に超伝導量子チップに回路を投入します。
キューの状態によっては、実際に回路が実行されるまでしばらく待たなければならない場合があります。
ただし、非同期実行のおかげで、すべてのタスクに関連付けられた一意のタスクIDを取得することでいつでも結果を参照することができます。

回路の実行プロセスは
AmazonBraketで学ぶ量子コンピュータ①で紹介させていただいた内容と同じように

① デバイスの定義
② 実行
③ 結果の取得
④ 結果の出力

の手順で実行することができます。
（以下のサンプルでは①デバイス定義と②実行の間で回路を定義したり、Z基底での測定を定義したりしています。）

# set up device ① デバイスの定義
rigetti = AwsDevice("arn:aws:braket:::device/qpu/rigetti/Aspen-8")

# 回路の定義
bell = Circuit().h(0).cnot(0, 1)  

# Z基底での測定
bell.expectation(Observable.Z() @ Observable.Z(), target=[0,1])

# run circuit with a polling time of 5 days ②実行
rigetti_task = rigetti.run(bell, s3_folder, shots=1000, poll_timeout_seconds=5*24*60*60)

# get id and status of submitted task　③ 結果の取得
rigetti_task_id = rigetti_task.id
rigetti_status = rigetti_task.state()
# print('ID of task:', rigetti_task_id)
print('Status of task:', rigetti_status)

「②実行」ではキューのタイムアウト時間を5日に設定していることがわかるかと思います。
実は今回は、上記サンプルでは「③結果の所得」までしか行えていません。
これは実機に投げる際に待ちが発生し、結果をすぐには取得できないため、今の状態を返してくれます。
標準的な状態としては「Status: CREATED」、「Status: QUEUED」、「Status: RUNNING」、「Status: COMPLETED」という状態（他にもCANCELED等もある）があり、おそらく実行直後は以下の通り、CREATEDになるかと思います。

Status of task: CREATED

ただし、注意したいのは実機が動いている時間であるかどうかということです。
そもそも実機が動いてない時間もあります。
もし実機が動いてない場合は以下のエラーが返ってきます。

DeviceOfflineException: An error occurred (DeviceOfflineException) when calling the CreateQuantumTask operation: Device is not available. Status = OFFLINE

動いている時間帯を確認したい場合は、こちらで確認できるので確認してみてください。

IonQ（実機）での実行

IonQに回路を投入します。Aspen-8に比べてキュー待ちが長い印象があるので結果がすぐに返ってこなくても気長に待つことをお勧めします。

一方でIonQにおいてもAspen-8と同じように実行できるので説明は割愛させていただきます。
サンプルコードを見てみると同じであることがわかるとおもいます。

唯一の違いは以下の通り実機の向き先を変更することのみです。

ionq = AwsDevice("arn:aws:braket:::device/qpu/ionq/ionQdevice")

Task Recovery

最後にタスクの復元の説明をします。
タスクのIDがわかれば AwsQuantumTask関数を用いてタスクを復元させることができます。

さらにタスクの状態がCOMPLETEDならば、タスクの詳細を取得できます。
例えば、以下のようなコードで結果を取得し、shot数がいくらであったか？そして、デバイスは何を使ったか？といったことを確認できます。

    rigetti_results = task_load.result()
    # print(rigetti_results)
    
    # get all metadata of submitted task
    metadata = task_load.metadata()
    # example for metadata
    shots = metadata['shots']
    machine = metadata['deviceArn']

また、Aspen-8の場合、回路最適化の結果等も以下の通り取得することができます。

    # get the compiled circuit
    print("The compiled circuit is:\n", rigetti_results.additional_metadata.rigettiMetadata.compiledProgram)
    

特にAspen-8はハードウェアとしてはRZ(θ), RX(k*π/2), CZ, XYがベースとなっているようで回路最適化を行い、これらの回路で表されるようになっているようです。
詳しくは こちらを見てみてください。

最後に

以上で「AmazonBraketで学ぶ量子コンピュータ③」を終わります。
今回は実機を使ってみたり、結果の復元を行ったりしてみました。
また別記事で他のBraketサンプルの解説を行ないながら量子コンピュータを学んでいける記事を書いていくので是非見てみてください。