この記事について
量子コンピュータの勉強をはじめて最近一通りAmazonBraketを触り終えました。
最近登場したサービスであることもあり、少し丁寧なドキュメントを残しておくと後続の方が勉強しやすくなったり、参照してわからないところを調べる際に便利かなと思ったので
自分自身の理解向上も兼ねて記事にまとめていこうと思います。
また、量子コンピュータ関係の他の記事は、下記で紹介しています。
※本記事は2021年2月に更新している記事です。更新などにより内容が変わっている可能性もあるのでご注意ください。
概要
本記事では量子コンピュータの導入部分に関して解説をしていこうと思います。
参照するのはこちらの0_Getting_started.ipynbというサンプルです。
こちらのサンプルは一般的なプログラミングでいうところのHello Worldを行っています。
説明に必要なコードは適宜こちらにも記載しながら説明していくのでよろしくお願いします。
前提知識
まず簡単に量子コンピュータ(ゲート型)を扱うのに必要な前提知識を説明していきます。
量子ビットの表現
量子コンピュータでのビット表現は既存の古典コンピュータのビット表現と大きく異なります。
古典ビットではビットを0, 1で表現しているのに対して、量子ビットでは2次元複素ベクトル空間での正規直交基底として各ビットを表現します。
それぞれのビットはディラックによって考案されたケット表記を用いて以下のように表現されます。
|0 \rangle =\begin{pmatrix} 1 \\ 0 \end{pmatrix}, \ \ \ \ \ |1 \rangle =\begin{pmatrix} 0 \\ 1 \end{pmatrix}
重ね合わせ
シュルテンゲルラッハの実験に代表されるように量子力学では「重ね合わせ」という特有の概念があります。
これは任意の量子状態を重み情報と位相情報が含まれた複素数 $\alpha, \beta$を用いて、以下のように表現できます。
|x\rangle = \alpha |0\rangle + \beta |1 \rangle = \alpha \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \beta \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} \alpha \\ \beta \end{pmatrix}
つまり量子ビット $|x \rangle$は$|0 \rangle$ と$|1 \rangle$の重ね合わせ状態からできています。
$|0 \rangle$ 状態は複素数の確率振幅$\alpha$ をもち、観測確率が $|\alpha|^2$で、$|1 \rangle$ 状態は確率振幅 $\beta$を持ち観測確率が $|\beta|^2$であることを示しており、以下のように規格化されています。
|\alpha|^2 + |\beta|^2 = 1
量子ゲート操作
量子ビットの操作は行列計算を用いた量子ゲート操作により実現されます。
例えば、何かしらの準備を行うことで $|0\rangle$を用意したとします。
これを $|1\rangle$に変更したいとき、以下のような操作を行わなければなりません。
|0\rangle \xrightarrow{X} |1\rangle
また、同じように$|1\rangle$ を用意した時に上記$X$の演算子は以下のように定義されるとします。
|1\rangle \xrightarrow{X} |0\rangle
つまり、 $X$ が $|0 \rangle, |1 \rangle $のそれぞれを入れ替える操作だとするとき、
|0 \rangle =\begin{pmatrix} 1 \\ 0 \end{pmatrix}, \ \ \ \ \ |1 \rangle =\begin{pmatrix} 0 \\ 1 \end{pmatrix}
なので
X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}
となります。
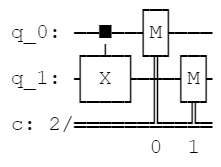
これを回路で示すと以下のようになります。
(回路の可視化はQiskitを用いて行っています。)

上記回路図は入力ビットに対してXゲートを操作した後、観測を行っているものとなります。(回路図上で示されるMという回路が観測を行うことを示しており、観測すると0, 1で示されるので二重線で表されています。)
$|0\rangle$ で入力を用意すると $|1\rangle$が観測され、$|1\rangle$ で入力を用意すると $|0\rangle$が観測されます。
上記、Xゲートは1量子ビットの反転操作を行うため、反転ゲートとも呼ばれます。
他にも1量子ビット操作では、位相・ビット反転ゲートのYゲートや位相反転ゲートのZゲート等が存在します。
以下のアダマールゲートを用いることで重ね合わせ状態を作ることができるのでそれも覚えておくと良いかと思います。
H = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}
2量子ビットの表記方法
AmazonBraketを使った説明に入る前に量子ビットが増えた状態だとどんな演算が行われるかの話を少しだけしていきます。
あまり増やして考えすぎても難しいだけなので2量子ビットの表記方法を整理します。
2つの演算子$A$と$B$を用意した時、それぞれが片方ずつの量子ビットに作用すると考えるとテンソル積を用いて以下のように示されます。
A\otimes B = \begin{pmatrix}
A_{00} \begin{pmatrix}
B_{00} & B_{01} \\
B_{10} & B_{11}
\end{pmatrix} & A_{01} \begin{pmatrix}
B_{00} & B_{01} \\
B_{10} & B_{11}
\end{pmatrix} \\
A_{10} \begin{pmatrix}
B_{00} & B_{01} \\
B_{10} & B_{11}
\end{pmatrix} & A_{11} \begin{pmatrix}
B_{00} & B_{01} \\
B_{10} & B_{11}
\end{pmatrix}
\end{pmatrix}.
ここで$A_{ij}, B_{kl}$はそれぞれの行列成分を示します。
つまり、2量子ビットは以下のようにテンソル積を用いて表すことができます。
\begin{split}\begin{equation}\begin{split}
\left|{00}\right\rangle &= \begin{pmatrix}
1 \begin{pmatrix}
1 \\
0
\end{pmatrix} \\
0 \begin{pmatrix}
1 \\
0
\end{pmatrix}
\end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \\0 \end{pmatrix}~~~\left|{01}\right\rangle = \begin{pmatrix}
1 \begin{pmatrix}
0 \\
1
\end{pmatrix} \\
0 \begin{pmatrix}
0 \\
1
\end{pmatrix}
\end{pmatrix} = \begin{pmatrix}0 \\ 1 \\ 0 \\ 0 \end{pmatrix}\end{split}
\end{equation}\end{split}
\begin{split}\begin{equation}\begin{split}\left|{10}\right\rangle = \begin{pmatrix}
0\begin{pmatrix}
1 \\
0
\end{pmatrix} \\
1\begin{pmatrix}
1 \\
0
\end{pmatrix}
\end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}
\left|{11}\right\rangle = \begin{pmatrix}
0 \begin{pmatrix}
0 \\
1
\end{pmatrix} \\
1\begin{pmatrix}
0 \\
1
\end{pmatrix}
\end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\1 \end{pmatrix}\end{split}
\end{equation}.\end{split}
なのでベクトルのそれぞれの成分が以下のように対応していることがわかると思います。
\begin{pmatrix} |{00}\rangle \\ |{01}\rangle \\ |{10}\rangle \\ |{11}\rangle \end{pmatrix}
2量子ビットの操作
2量子ビットの表記方法がわかったので最後に2量子ビットの操作について例を挙げて簡単に触れておきます。
2ビットの量子演算を行うのに最も頻繁に用いられるものはCNOTゲート(制御NOTゲート)です。
これは0量子ビット目が$|1 \rangle $ の時に 1量子ビット目のビットを反転させる操作を行います。
(今回は0量子ビット目を制御ビットと考えましたが、1量子ビット目を制御ビットと考えて「1量子ビット目が$|1 \rangle $ の時に 0量子ビット目のビットを反転させる操作」と考えても問題ありません。反転させる方をターゲットビット、条件を与える方を制御ビットと覚えておけば良いと思います。)
具体的には、
\begin{pmatrix} |{00}\rangle \\ |{01}\rangle \\ |{\color{blue}1\color{red}0}\rangle \\ |{\color{blue}1\color{red}1}\rangle \end{pmatrix} \xrightarrow{CNOT} \begin{pmatrix} |{00}\rangle \\ |{01}\rangle \\ |{\color{blue}1\color{red}1}\rangle \\ |{\color{blue}1\color{red}0}\rangle \end{pmatrix}
の操作を行う演算を示します。
かなりかいつまんで説明すると上記は $|10\rangle, |11\rangle$の反転だととらえて、上記は以下のような行列計算を示すことができます。
CNOT =
\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 1\\
0 & 0 & 1 & 0
\end{pmatrix}.
回路図に示すと以下のようになります。
ここではかなり簡単にCNOTの話を記載しましたが、もう少し詳細を知りたい方はこちらを参考にしてみてください。
AmazonBraket
ここから実際にAmazonBraketを使って説明していきます。
まずはこちらの記事やドキュメントなどを参考に環境を用意してください。
環境を用意すると以下のようにデフォルトでサンプルコードがGitHubからインポートされています。
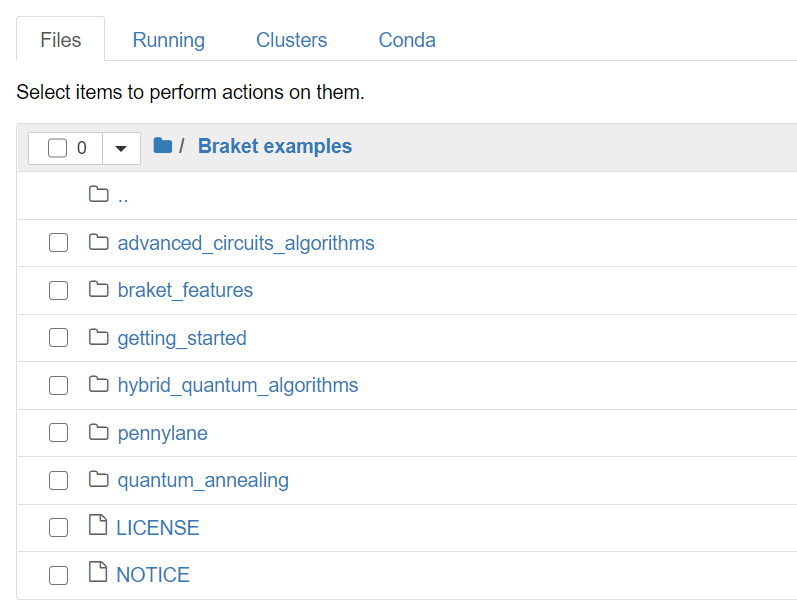
今回はこの配下にある
getting_started/0_Getting_started.ipynb
を見ていきます。
全体概要
こちらでは導入としてベル回路の作成を行い、シミュレータで実際に量子回路を実行し、結果を観測しています。
ベル回路では以下のようにアダマールゲートと制御NOTゲートを組み合わせて量子もつれ状態を作る回路を作成していきます。
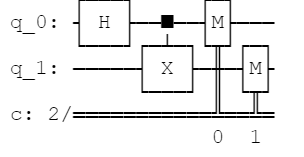
はじめに $|00 \rangle$の状態を用意します。
その後、0ビット目にアダマールゲートを適用すると以下のような量子状態となります。
\Bigl(\frac{1}{\sqrt{2}} |0 \rangle + \frac{1}{\sqrt{2}} |1 \rangle \Bigr) \ |0 \rangle = \frac{1}{\sqrt{2}} |00 \rangle + \frac{1}{\sqrt{2}} |\color{blue}1\color{red}0 \rangle
これに制御NOTゲートを適用すると0番目の量子ビットが1の時に1番目の量子ビットが反転するので最終的に以下の量子状態をとることになります。
\frac{1}{\sqrt{2}} |00 \rangle + \frac{1}{\sqrt{2}} |\color{blue}1\color{red}1\rangle
これを観測すると、00状態と11状態が半分ずつの確率で取り出せることがわかります。
解説
ここからは実際にサンプルコードを使って解説していきます。
import
可視化をするために matplotlibをインポートする以外はAmazonBraketのSDKをインポートすることになります。
回路設計を行う上では常にCircuitモジュールをインストールすることになるのであまり気にする必要はありませんが、
デバイスを使用する際にローカルシミュレータを使用するときは LocalSimulatorモジュールをインストールしなければならないので気をつけてください。
回路の定義
AmazonBraketを使用する際は簡単に回路を定義できます。
ベル回路、つまり
「アダマールゲートを0量子ビットに適用した後、0量子ビット目を制御ビットとし、1量子ビット目をターゲットビットとして定義したCNOTゲート」
を適用するような回路は以下のように定義します。
# build a Bell state with two qubits. Here 'cnot(control=0, target=1)' can be simplified as 'cnot(0,1)'
bell = Circuit().h(0).cnot(control=0, target=1)
これでベル回路の定義ができました。
実行
量子コンピュータを実行する際は以下のような手順で実行します。
① デバイスの定義
② 実行
③ 結果の取得
④ 結果の出力
「①デバイスの定義」では今回紹介のサンプルではローカルシミュレータを定義していますが、こちらを実機に向けることで変更点はこの箇所のみで量子コンピュータを実行できるようになります。
あまりほかのソースコードを変えずに実機の向き先を変えることができるので便利な機能の一つと言えます。
「②実行」ではどのような定義した回路を実行することができます。サンプルコードでは shots数(サンプリング回数)を定義していますが、こちら定義しなかった場合はデフォルトの1024回が実行されることになります。
(AmazonBraketで実機を使用する場合はタスク数とshots数が課金単位となりますので是非確認の上使用してみてください。Localsimulatorではタスク数とshots数には依存せず料金を気にせずに実行できるので料金面気にする場合はLocalsimulatorで行うのが良いかと思います。)
「③結果(観測値)の取得」では実際に観測された値を取得することができます。
※どのような値が取得できるかは別記事で紹介します。特にLocalsimulatorはあくまで古典コンピュータでシミュレートするため様々な情報を取得することができるのでうまく使ってみてください。
「④結果の出力」では「③結果(観測値)の取得」で取得された結果を出力します。
ソースコードに示すと以下の通りになります。
# ① デバイスの定義
device = LocalSimulator()
# ② 実行
result = device.run(bell, shots=1000).result()
# ③ 結果(観測値)の取得
counts = result.measurement_counts
# ④ 結果の出力
print(counts)
実際に出力された結果は以下になります。
Counter({'11': 505, '00': 495})
ランダム性のあるものなので毎回結果が異なります。
試しに何度も実行してみると良いかと思います。
少しだけ補足すると、量子コンピュータの実機だともちろんランダム性をもともと備えているので上記のようなサンプリング結果となります。
ローカルシミュレータとはいえ、上記の量子コンピュータの性質をエミュレートしているため、同じようにランダム性のある結果を取得できます。
可視化
最後に可視化です。
可視化は以下の通り、matplotlibを使って行われます。
# plot using Counter
plt.bar(counts.keys(), counts.values())
plt.xlabel('bitstrings')
plt.ylabel('counts')
期待通り、およそ1:1の確率で 11, 00 が獲得されたことがわかるかと思います。
最後に
以上で「AmazonBraketで学ぶ量子コンピュータ①」を終わります。
今回は導入部分の解説を行ってみました。
また別記事で他のBraketサンプルの解説を行ないながら量子コンピュータを学んでいける記事を書いていくので是非見てみてください。