マクドナルドの記事を量子コンピュータでやってみた

こんな記事を見つけました

最近、こんな記事を見つけました。
「マクドナルドで一日分の栄養を取れる組み合わせを計算したら衝撃の結果に」
私も数理最適化をかじっている者なので何かやってみたいな。
と思ったのところ、せっかくなので今勉強中の量子コンピュータでやっちゃいましょう。
と思ってしまったのでやってみます。
上記記事と構成をなるべく同じにしてわかりやすくするというスタンスは保ちつつ、量子コンピュータの特性を踏まえて変えなければならないところもあるのでその辺も明確にしていこうと思います。

また、量子コンピュータ関係の他の記事は、下記で紹介しています。

定式化

目的関数

目的関数については参照している記事に準拠して
「一日必要な栄養素を満たす最もカロリーの低い商品の組み合わせ」とします。
金に糸目をつけないことも準拠します。

制約

基本的な制約は上記記事と同じで以下の栄養素を満たすように最適化していきます。

栄養素	基準量
たんぱく質 (g)	179※1
脂質 (g)	75※1
炭水化物 (g)	675※1
ナトリウム (mg)	5000
カリウム (mg)	3000
カルシウム (mg)	738
リン (mg)	600
鉄 (mg)	6.3
ビタミンA (μg)	625
ビタミンB1 (mg)	1.4
ビタミンB2 (mg)	1.6
ナイアシン (mg)	15
ビタミンC (mg)	100
コレステロール (mg)	0
食物繊維 (g)	21
食塩相当量 (g)	5

ただし、量子コンピュータの特性上、いくつか別の制約を追加します。

変更する制約

ここでは変更する制約に関して述べていきます。

1. 「最低限必要な栄養素」ではなく、「なるべく基準量と同じぐらい」という制約
2. それぞれの商品を複数頼むことはできない

といった制約をかけることとします。
1つ目の制約も2つ目の制約もなしにはできますが、現状の量子コンピュータでは多くの変数を扱うことができないため、変数の節約も含めて上記のような制約をかけています。

QUBO (Quadratic Unconstrained Binary Optimization：制約なし二次形式二値変数最適化)

量子コンピュータで最適化問題を解くには、QUBO (Quadratic Unconstrained Binary Optimization：制約なし二次形式二値変数最適化)形式に問題を書き換える必要があります。
こちらの説明を引用させていただくとQUBOとは

Quadratic Unconstrained Binary Optimization (制約なし二次形式二値変数最適化)の略。D-Wave 2000QまでのD-Waveマシンがネイティブに扱える問題の形式。
0または1, あるいは +1または-1といった二値のみを取れる被最適化変数$x_i$に対して、目的関数が変数の2次の項までで記述ができ（$x_ix_jx_k$などの3次以上の項を含まない）、かつ、$\Sigma^{N}_{i=1}x_i<C$のような明示的な制約を含まない問題に対する最適化のことを意味している。

といった問題のことです。
特にポイントなのは「$\Sigma^{N}_{i=1}x_i<C$のような明示的な制約を含まない」といった点にあります。
これはあくまで明示的な制約を含まない。といっているので工夫してやることで制約を表すことができます。

とりあえずQUBOがどんな式で表されるかを示すと、以下のように示されます。

f = \sum_{i=1}^n \sum_{j=1}^i q_{ij} x_i x_j

ここで $x_i$は $0, 1$ のいずれかの値をとり、$q_{ij}$ は$1\leq j\leq i\leq n$に対する$x_{i}$と$x_{j}$の相互作用を示します。（ちなみに$i = j$の時、$x_i = x_j, x_ix_j = x_i^{2} = x_i$ となります。($x_i = {0, 1}$)）

2. それぞれの商品を複数頼むことはできない

といった制約はこの0, 1変数しか取れない構造によるものだということがわかったかと思います。

マクドナルド問題定式化

今回解きたい問題の定式化をしていきます。
まず目的関数は

f_{obj} = \sum_{i=1}^n a_{i} x_i

$a_{i}$は$i$番目の商品のカロリーを示します。これを最小化していきます。

次に制約です。明示的な制約を含むことができないのでどうするかというと、QUBOの定式にペナルティ付きで埋め込んであげます。
つまり、重みをかけて最適化関数に入れてあげることでなるべく守ってくれ～。という処理を加えるイメージです。
$k$番目の栄養素に対する基準値を $b_k$ とし、それぞれの商品$i$に対する $k$番目の要素の含有量を$c_{ik}$とすると

f_{con} = \sum_{k=1}^N \bigl( \sum_{i=1}^n c_{ik}x_i - b_k \bigr)^2

と示されます。
例えば、$k$番目の栄養素の基準値$b_k$が100の時に、$ \sum_{i=1}^n c_{ik}x_i$で示される栄養を取りすぎて $ \sum_{i=1}^n c_{ik}x_i = 150$ も栄養素をとってしまったとします。
その時には$(150 - 100)^2 = 2500$が目的関数に加えられるわけです。
これをなるべく小さく、つまり、$ \sum_{i=1}^n c_{ik}x_i = 100$になるように最適化する構造をとります。
ここで

1. 「最低限必要な栄養素」ではなく、「なるべく基準量と同じぐらい」という制約

という制約を思い出してください。
上記2乗した定式化だと栄養素の基準値$b_k$より小さくても大きくても$f_{con}$の値が大きくなることがわかるかと思います。
定式化を工夫すれば小さい場合のみや大きい場合のみといった制約のかけ方もできますが、今回は大きく外さなければ良さそうなので定式化としてはこのままとして、制約の意味を少しだけ変えました。

最終的に、制約を満たしながら元の目的関数を最適化したいので、

f = \sum_{i=1}^n a_{i} x_i + A \sum_{k=1}^N \bigl( \sum_{i=1}^n c_{ik}x_i - b_k \bigr)^2

といったQUBOを最適化していくことになります。（$A$はペナルティ）

実装

マクドナルドで一日分の栄養を取れる組み合わせを計算したら衝撃の結果に

商品の数が96個、栄養素の数が16個なので、とても人間の手では解けません。そこでコンピューターの力を借ります。

といった点、本記事でも変わりません。
なので量子コンピュータに解かせるわけですが、そもそも定式化も面倒なのが今回です。
ということで、先人の知恵を借りようかと思います。
定式化ではPyQUBOというQUBO化のツールを使用します。

また、今回使う量子コンピュータはAmazonBraketで提供している「D-Wave — Advantage_system1.1」です。
使ってみたい方は是非、「こちらの記事」等を参照に使ってみてください。

定式化部分

PyQUBOを用いて定式化をお行います。
詳しくはドキュメントを参照していただけると幸いです。

from pyqubo import Array, Binary, Placeholder, Constraint

# 変数の定義
AA = Binary("AA")
AB = Binary("AB")
AC = Binary("AC")
AD = Binary("AD")
AE = Binary("AE")
AF = Binary("AF")
AG = Binary("AG")
AH = Binary("AH")
AI = Binary("AI")
AJ = Binary("AJ")
AK = Binary("AK")
AL = Binary("AL")
AM = Binary("AM")
AN = Binary("AN")
AO = Binary("AO")
AP = Binary("AP")
AQ = Binary("AQ")
AR = Binary("AR")
AS = Binary("AS")
AT = Binary("AT")
AU = Binary("AU")
AV = Binary("AV")
AW = Binary("AW")
AX = Binary("AX")
AY = Binary("AY")
AZ = Binary("AZ")
BA = Binary("BA")
BB = Binary("BB")
BC = Binary("BC")
BD = Binary("BD")
BE = Binary("BE")
BF = Binary("BF")
BG = Binary("BG")
BH = Binary("BH")
BI = Binary("BI")
BJ = Binary("BJ")
BK = Binary("BK")
BL = Binary("BL")
BM = Binary("BM")
BN = Binary("BN")
BO = Binary("BO")
BP = Binary("BP")
BQ = Binary("BQ")
BR = Binary("BR")
BS = Binary("BS")
BT = Binary("BT")
BU = Binary("BU")
BV = Binary("BV")
BW = Binary("BW")
BX = Binary("BX")
BY = Binary("BY")
BZ = Binary("BZ")
CA = Binary("CA")
CB = Binary("CB")
CC = Binary("CC")
CD = Binary("CD")
CE = Binary("CE")
CF = Binary("CF")
CG = Binary("CG")
CH = Binary("CH")
CI = Binary("CI")
CJ = Binary("CJ")
CK = Binary("CK")
CL = Binary("CL")
CM = Binary("CM")
CN = Binary("CN")
CO = Binary("CO")
CP = Binary("CP")
CQ = Binary("CQ")
CR = Binary("CR")
CS = Binary("CS")
CT = Binary("CT")
CU = Binary("CU")
CV = Binary("CV")
CW = Binary("CW")
CX = Binary("CX")
CY = Binary("CY")
CZ = Binary("CZ")
DA = Binary("DA")
DB = Binary("DB")
DC = Binary("DC")
DD = Binary("DD")
DE = Binary("DE")
DF = Binary("DF")
DG = Binary("DG")
DH = Binary("DH")
DI = Binary("DI")
DJ = Binary("DJ")
DK = Binary("DK")
DL = Binary("DL")
DM = Binary("DM")
DN = Binary("DN")
DO = Binary("DO")
DP = Binary("DP")
DQ = Binary("DQ")
DR = Binary("DR")

# 元の目的関数
obj = 395*AA+ 545*AB+ 532*AC+ 441*AD+ 498*AE+ 478*AF+ 387*AG+ 311*AH+ 1067*AI+ 428*AJ+ 527*AK+ 489*AL+ 776*AM+ 38*AN+ 389*AO+ 475*AP+ 395*AQ+ 457*AR+ 307*AS+ 431*AT+ 345*AU+ 364*AV+ 465*AW+ 256*AX+ 60*AY+ 979*AZ+ 659*BA+ 525*BB+ 323*BC+ 292*BD+ 374*BE+ 319*BF+ 121*BG+ 419*BH+ 420*BI+ 550*BJ+ 396*BK+ 695*BL+ 1*BM+ 553*BN+ 768*BO+ 728*BP+ 486*BQ+ 594*BR+ 693*BS+ 655*BT+ 542*BU+ 655*BV+ 406*BW+ 584*BX+ 498*BY+ 709*BZ+ 356*CA+ 724*CB+ 434*CC+ 473*CD+ 642*CE+ 625*CF+ 471*CG+ 579*CH+ 558*CI+ 83*CJ+ 31*CK+ 287*CL+ 23*CM+ 10*CN+ 1034*CO+ 252*CP+ 8*CQ+ 249*CR+ 6*CS+ 243*CT+ 275*CU+ 148*CV+ 810*CW+ 270*CX+ 109*CY+ 145*CZ+ 33*DA+ 161*DB+ 304*DC+ 211*DD+ 1057*DE+ 1844*DF+ 44*DG+ 517*DH+ 410*DI+ 225*DJ+ 235*DK+ 337*DL+ 59*DM+ 257*DN+ 295*DO+ 232*DP+ 108*DQ+ 7*DR

# それぞれの栄養素に対する制約項（差の二乗を計算）
con1 = (12.5*AA+ 14.5*AB+ 19*AC+ 16.7*AD+ 20.2*AE+ 15.5*AF+ 22.3*AG+ 19.2*AH+ 61.9*AI+ 19.9*AJ+ 26.5*AK+ 27.3*AL+ 39.5*AM+ 0*AN+ 14.2*AO+ 21.5*AP+ 15*AQ+ 26.5*AR+ 15.8*AS+ 17.1*AT+ 14*AU+ 15.2*AV+ 20*AW+ 12.8*AX+ 0*AY+ 34.1*AZ+ 26.2*BA+ 26*BB+ 14.4*BC+ 15.9*BD+ 17.7*BE+ 8*BF+ 0*BG+ 17.2*BH+ 10.4*BI+ 20.3*BJ+ 15.7*BK+ 29.7*BL+ 0*BM+ 19.4*BN+ 35.3*BO+ 25.8*BP+ 30*BQ+ 33.3*BR+ 39.8*BS+ 40.6*BT+ 23.2*BU+ 42*BV+ 23.5*BW+ 26.1*BX+ 23*BY+ 34.8*BZ+ 20.6*CA+ 41.4*CB+ 22.7*CC+ 25.5*CD+ 27.2*CE+ 39*CF+ 26.7*CG+ 21.4*CH+ 32.4*CI+ 5.2*CJ+ 0.2*CK+ 3*CL+ 0.4*CM+ 0.5*CN+ 13.4*CO+ 15.3*CP+ 0.5*CQ+ 15*CR+ 0.2*CS+ 14.8*CT+ 5*CU+ 3.8*CV+ 47.3*CW+ 15.8*CX+ 0.3*CY+ 1.2*CZ+ 0.2*DA+ 3.8*DB+ 3.7*DC+ 1.9*DD+ 38.2*DE+ 60.6*DF+ 0.4*DG+ 6.7*DH+ 5.3*DI+ 2.9*DJ+ 5.9*DK+ 8*DL+ 3.2*DM+ 5.4*DN+ 5.9*DO+ 5.3*DP+ 0.4*DQ+ 0.4*DR - 0.65)**2
con2 = (17.4*AA+ 29.4*AB+ 21.1*AC+ 20*AD+ 23.2*AE+ 30.2*AF+ 18.9*AG+ 13.5*AH+ 65.5*AI+ 21.7*AJ+ 30.7*AK+ 26.6*AL+ 43.1*AM+ 0*AN+ 20.2*AO+ 30.6*AP+ 25.1*AQ+ 25*AR+ 13.4*AS+ 23*AT+ 15.5*AU+ 17.3*AV+ 21.9*AW+ 9.4*AX+ 6.7*AY+ 51.3*AZ+ 42.7*BA+ 28.3*BB+ 13.9*BC+ 13.3*BD+ 20.8*BE+ 8.6*BF+ 0*BG+ 23.7*BH+ 23.8*BI+ 33.2*BJ+ 18.1*BK+ 49.7*BL+ 0*BM+ 25.5*BN+ 36.1*BO+ 50*BP+ 26.5*BQ+ 34.2*BR+ 43.2*BS+ 39.1*BT+ 28.7*BU+ 40.1*BV+ 21*BW+ 31.6*BX+ 24*BY+ 34.7*BZ+ 16.9*CA+ 43.4*CB+ 18.6*CC+ 28.4*CD+ 43.5*CE+ 36.2*CF+ 23.7*CG+ 38.3*CH+ 33.1*CI+ 3*CJ+ 1.5*CK+ 18*CL+ 0*CM+ 0.1*CN+ 51.8*CO+ 13.1*CP+ 0.2*CQ+ 12.9*CR+ 0*CS+ 12.8*CT+ 18.9*CU+ 3.9*CV+ 51.6*CW+ 17.2*CX+ 11.2*CY+ 9.6*CZ+ 0.1*DA+ 4.4*DB+ 18.1*DC+ 10.7*DD+ 60.3*DE+ 103.4*DF+ 2.3*DG+ 25.9*DH+ 20.6*DI+ 11.3*DJ+ 7*DK+ 10.6*DL+ 0.8*DM+ 5.5*DN+ 10.7*DO+ 5.5*DP+ 10.9*DQ+ 0*DR - 25) ** 2
con3 = (47.7*AA+ 55.8*AB+ 66.6*AC+ 48.4*AD+ 52.4*AE+ 36.4*AF+ 31*AG+ 27.1*AH+ 57.5*AI+ 38.9*AJ+ 36.8*AK+ 35.5*AL+ 57.5*AM+ 9.5*AN+ 38.1*AO+ 27.3*AP+ 27.2*AQ+ 31.4*AR+ 30.8*AS+ 39.2*AT+ 37.7*AU+ 37*AV+ 47.3*AW+ 30.3*AX+ 0*AY+ 92.9*AZ+ 40.2*BA+ 41.8*BB+ 35.8*BC+ 26.4*BD+ 29.1*BE+ 52.7*BF+ 30.2*BG+ 34.3*BH+ 41.9*BI+ 42.4*BJ+ 42.4*BK+ 31.2*BL+ 0.1*BM+ 62.8*BN+ 76*BO+ 44.1*BP+ 31*BQ+ 38.9*BR+ 36.8*BS+ 35.5*BT+ 48*BU+ 31.4*BV+ 30.8*BW+ 49.1*BX+ 47.6*BY+ 64.4*BZ+ 30.3*CA+ 41.8*CB+ 45*CC+ 29.1*CD+ 35.5*CE+ 36.3*CF+ 38.2*CG+ 37.6*CH+ 32.7*CI+ 9.6*CJ+ 4.3*CK+ 28.3*CL+ 5.6*CM+ 2.3*CN+ 128.5*CO+ 18.2*CP+ 1.1*CQ+ 18.3*CR+ 1.2*CS+ 17.2*CT+ 21.1*CU+ 24.7*CV+ 39.2*CW+ 13.1*CX+ 1.6*CY+ 13.3*CZ+ 7.7*DA+ 26.4*DB+ 31.5*DC+ 26.8*DD+ 90.4*DE+ 167.7*DF+ 5.2*DG+ 64.3*DH+ 51*DI+ 28*DJ+ 37.7*DK+ 53.4*DL+ 9.7*DM+ 46.8*DN+ 44.1*DO+ 40.6*DP+ 2*DQ+ 1.2*DR - 62.5) ** 2
con4 = (919*AA+ 986*AB+ 1296*AC+ 994*AD+ 1216*AE+ 829*AF+ 813*AG+ 649*AH+ 2326*AI+ 816*AJ+ 1052*AK+ 1129*AL+ 1714*AM+ 4*AN+ 996*AO+ 789*AP+ 722*AQ+ 1132*AR+ 747*AS+ 1060*AT+ 850*AU+ 813*AV+ 1139*AW+ 542*AX+ 36*AY+ 1673*AZ+ 962*BA+ 1007*BB+ 644*BC+ 636*BD+ 837*BE+ 711*BF+ 1*BG+ 890*BH+ 971*BI+ 1193*BJ+ 1030*BK+ 1358*BL+ 254*BM+ 1309*BN+ 2082*BO+ 1308*BP+ 965*BQ+ 987*BR+ 1223*BS+ 1300*BT+ 1501*BU+ 1435*BV+ 898*BW+ 1565*BX+ 1355*BY+ 1778*BZ+ 693*CA+ 1310*CB+ 816*CC+ 989*CD+ 1142*CE+ 1428*CF+ 1340*CG+ 1245*CH+ 1554*CI+ 84*CJ+ 2*CK+ 222*CL+ 210*CM+ 1*CN+ 830*CO+ 791*CP+ 152*CQ+ 730*CR+ 91*CS+ 639*CT+ 55*CU+ 83*CV+ 1517*CW+ 506*CX+ 283*CY+ 307*CZ+ 182*DA+ 318*DB+ 154*DC+ 217*DD+ 1426*DE+ 2346*DF+ 182*DG+ 415*DH+ 329*DI+ 181*DJ+ 155*DK+ 268*DL+ 37*DM+ 135*DN+ 118*DO+ 118*DP+ 222*DQ+ 384*DR - 25) ** 2
con5 = (119*AA+ 237*AB+ 328*AC+ 212*AD+ 343*AE+ 255*AF+ 297*AG+ 183*AH+ 860*AI+ 366*AJ+ 432*AK+ 379*AL+ 536*AM+ 7*AN+ 262*AO+ 235*AP+ 170*AQ+ 358*AR+ 232*AS+ 277*AT+ 246*AU+ 258*AV+ 345*AW+ 214*AX+ 0*AY+ 730*AZ+ 477*BA+ 372*BB+ 198*BC+ 148*BD+ 230*BE+ 254*BF+ 0*BG+ 266*BH+ 167*BI+ 256*BJ+ 172*BK+ 415*BL+ 2*BM+ 138*BN+ 610*BO+ 433*BP+ 405*BQ+ 551*BR+ 617*BS+ 565*BT+ 445*BU+ 574*BV+ 340*BW+ 460*BX+ 430*BY+ 596*BZ+ 322*CA+ 588*CB+ 342*CC+ 338*CD+ 428*CE+ 523*CF+ 467*CG+ 294*CH+ 401*CI+ 206*CJ+ 7*CK+ 30*CL+ 103*CM+ 137*CN+ 2260*CO+ 256*CP+ 5*CQ+ 259*CR+ 8*CS+ 251*CT+ 191*CU+ 179*CV+ 786*CW+ 262*CX+ 6*CY+ 194*CZ+ 45*DA+ 112*DB+ 219*DC+ 55*DD+ 1654*DE+ 3046*DF+ 14*DG+ 1130*DH+ 897*DI+ 492*DJ+ 280*DK+ 347*DL+ 118*DM+ 235*DN+ 253*DO+ 215*DP+ 16*DQ+ 30*DR - 3000) ** 2
con6 = (64*AA+ 33*AB+ 20*AC+ 103*AD+ 38*AE+ 51*AF+ 146*AG+ 171*AH+ 259*AI+ 42*AJ+ 134*AK+ 217*AL+ 250*AM+ 1*AN+ 33*AO+ 183*AP+ 158*AQ+ 216*AR+ 121*AS+ 124*AT+ 31*AU+ 62*AV+ 39*AW+ 30*AX+ 1*AY+ 257*AZ+ 123*BA+ 143*BB+ 75*BC+ 137*BD+ 122*BE+ 134*BF+ 0*BG+ 50*BH+ 79*BI+ 188*BJ+ 174*BK+ 200*BL+ 1*BM+ 97*BN+ 48*BO+ 76*BP+ 149*BQ+ 47*BR+ 140*BS+ 223*BT+ 39*BU+ 223*BV+ 124*BW+ 130*BX+ 37*BY+ 48*BZ+ 33*CA+ 149*CB+ 80*CC+ 125*CD+ 73*CE+ 232*CF+ 139*CG+ 231*CH+ 394*CI+ 27*CJ+ 4*CK+ 10*CL+ 4*CM+ 13*CN+ 45*CO+ 33*CP+ 23*CQ+ 12*CR+ 2*CS+ 10*CT+ 134*CU+ 121*CV+ 31*CW+ 10*CX+ 4*CY+ 5*CZ+ 2*DA+ 60*DB+ 44*DC+ 5*DD+ 43*DE+ 76*DF+ 5*DG+ 22*DH+ 18*DI+ 10*DJ+ 174*DK+ 181*DL+ 89*DM+ 143*DN+ 144*DO+ 136*DP+ 3*DQ+ 3*DR - 738) ** 2
con7 = (102*AA+ 149*AB+ 319*AC+ 214*AD+ 320*AE+ 149*AF+ 274*AG+ 211*AH+ 596*AI+ 171*AJ+ 300*AK+ 334*AL+ 428*AM+ 1*AN+ 227*AO+ 211*AP+ 121*AQ+ 318*AR+ 184*AS+ 301*AT+ 222*AU+ 225*AV+ 319*AW+ 109*AX+ 2*AY+ 273*AZ+ 273*BA+ 275*BB+ 205*BC+ 235*BD+ 215*BE+ 0*BF+ 1*BG+ 172*BH+ 372*BI+ 535*BJ+ 499*BK+ 245*BL+ 0*BM+ 143*BN+ 588*BO+ 246*BP+ 332*BQ+ 273*BR+ 402*BS+ 436*BT+ 400*BU+ 435*BV+ 242*BW+ 475*BX+ 395*BY+ 583*BZ+ 167*CA+ 392*CB+ 328*CC+ 273*CD+ 265*CE+ 422*CF+ 312*CG+ 296*CH+ 461*CI+ 80*CJ+ 4*CK+ 26*CL+ 8*CM+ 16*CN+ 497*CO+ 282*CP+ 18*CQ+ 266*CR+ 3*CS+ 264*CT+ 140*CU+ 125*CV+ 758*CW+ 253*CX+ 10*CY+ 47*CZ+ 5*DA+ 0*DB+ 75*DC+ 23*DD+ 754*DE+ 1255*DF+ 11*DG+ 249*DH+ 198*DI+ 108*DJ+ 187*DK+ 218*DL+ 70*DM+ 154*DN+ 167*DO+ 151*DP+ 7*DQ+ 9*DR - 600) ** 2
con8 = (0.8*AA+ 0.9*AB+ 0.8*AC+ 1.1*AD+ 0.9*AE+ 1.1*AF+ 2.1*AG+ 1.3*AH+ 5.2*AI+ 1.9*AJ+ 2.1*AK+ 1.9*AL+ 3.1*AM+ 0*AN+ 0.8*AO+ 1.7*AP+ 0.8*AQ+ 2*AR+ 1.2*AS+ 0.8*AT+ 0.7*AU+ 0.7*AV+ 0.9*AW+ 1.2*AX+ 0*AY+ 6.2*AZ+ 2.9*BA+ 2.2*BB+ 0.5*BC+ 1.3*BD+ 1.3*BE+ 3.3*BF+ 0*BG+ 1.1*BH+ 2*BI+ 3.1*BJ+ 2.5*BK+ 2.3*BL+ 0*BM+ 1*BN+ 1.4*BO+ 1.8*BP+ 2.8*BQ+ 3.2*BR+ 3.4*BS+ 3.2*BT+ 1.1*BU+ 3.5*BV+ 1.9*BW+ 1.1*BX+ 1*BY+ 1.3*BZ+ 1.9*CA+ 3.8*CB+ 0.6*CC+ 2.1*CD+ 1.7*CE+ 3.2*CF+ 2.2*CG+ 1.1*CH+ 2*CI+ 1.1*CJ+ 0*CK+ 0.1*CL+ 0.1*CM+ 0.2*CN+ 2.6*CO+ 0.5*CP+ 0*CQ+ 0.5*CR+ 0*CS+ 0.4*CT+ 0.3*CU+ 0*CV+ 1.4*CW+ 0.5*CX+ 0*CY+ 0.3*CZ+ 0.1*DA+ 1.4*DB+ 2.9*DC+ 0.3*DD+ 2.2*DE+ 4*DF+ 0.1*DG+ 1.3*DH+ 1*DI+ 0.6*DJ+ 0.5*DK+ 1.5*DL+ 0*DM+ 0.2*DN+ 0.4*DO+ 0.1*DP+ 0.1*DQ+ 0.1*DR - 6.3) ** 2
con9 = (8*AA+ 10*AB+ 11*AC+ 60*AD+ 10*AE+ 11*AF+ 131*AG+ 118*AH+ 149*AI+ 63*AJ+ 114*AK+ 147*AL+ 127*AM+ 0*AN+ 25*AO+ 118*AP+ 48*AQ+ 118*AR+ 61*AS+ 62*AT+ 13*AU+ 13*AV+ 12*AW+ 14*AX+ 99*AY+ 141*AZ+ 141*BA+ 74*BB+ 28*BC+ 118*BD+ 61*BE+ 0*BF+ 0*BG+ 8*BH+ 9*BI+ 125*BJ+ 115*BK+ 123*BL+ 0*BM+ 9*BN+ 14*BO+ 17*BP+ 141*BQ+ 78*BR+ 129*BS+ 161*BT+ 35*BU+ 137*BV+ 71*BW+ 72*BX+ 22*BY+ 16*BZ+ 23*CA+ 93*CB+ 30*CC+ 71*CD+ 14*CE+ 124*CF+ 82*CG+ 108*CH+ 217*CI+ 7*CJ+ 1*CK+ 7*CL+ 9*CM+ 27*CN+ 0*CO+ 7*CP+ 3*CQ+ 10*CR+ 6*CS+ 4*CT+ 255*CU+ 42*CV+ 69*CW+ 23*CX+ 3*CY+ 0*CZ+ 3*DA+ 8*DB+ 4*DC+ 1*DD+ 46*DE+ 69*DF+ 1*DG+ 0*DH+ 0*DI+ 0*DJ+ 61*DK+ 61*DL+ 10*DM+ 47*DN+ 47*DO+ 47*DP+ 5*DQ+ 0*DR - 625) ** 2
con10 = (0.09*AA+ 0.16*AB+ 0.13*AC+ 0.11*AD+ 0.16*AE+ 0.19*AF+ 0.13*AG+ 0.13*AH+ 0.31*AI+ 0.17*AJ+ 0.24*AK+ 0.18*AL+ 0.23*AM+ 0*AN+ 0.11*AO+ 0.18*AP+ 0.15*AQ+ 0.13*AR+ 0.1*AS+ 0.11*AT+ 0.12*AU+ 0.15*AV+ 0.16*AW+ 0.1*AX+ 0*AY+ 0.25*AZ+ 0.25*BA+ 0.17*BB+ 0.11*BC+ 0.14*BD+ 0.14*BE+ 0*BF+ 0*BG+ 0.26*BH+ 0.3*BI+ 0.32*BJ+ 0.23*BK+ 0.28*BL+ 0*BM+ 0.1*BN+ 0.26*BO+ 0.32*BP+ 0.16*BQ+ 0.21*BR+ 0.28*BS+ 0.22*BT+ 0.16*BU+ 0.18*BV+ 0.13*BW+ 0.16*BX+ 0.17*BY+ 0.26*BZ+ 0.12*CA+ 0.22*CB+ 0.17*CC+ 0.16*CD+ 0.39*CE+ 0.19*CF+ 0.25*CG+ 0.2*CH+ 0.14*CI+ 0.1*CJ+ 0*CK+ 0.04*CL+ 0.02*CM+ 0.03*CN+ 0.61*CO+ 0.1*CP+ 0*CQ+ 0.31*CR+ 0.22*CS+ 0.09*CT+ 0.05*CU+ 0.05*CV+ 0.28*CW+ 0.09*CX+ 0.01*CY+ 0.05*CZ+ 0.01*DA+ 0*DB+ 0.08*DC+ 0.05*DD+ 0.5*DE+ 0.9*DF+ 0.01*DG+ 0.31*DH+ 0.24*DI+ 0.13*DJ+ 0.07*DK+ 0.09*DL+ 0.03*DM+ 0.07*DN+ 0.07*DO+ 0.07*DP+ 0.01*DQ+ 0.01*DR - 1.4) ** 2
con11 = (0.06*AA+ 0.16*AB+ 0.09*AC+ 0.14*AD+ 0.12*AE+ 0.19*AF+ 0.36*AG+ 0.31*AH+ 0.54*AI+ 0.16*AJ+ 0.25*AK+ 0.3*AL+ 0.38*AM+ 0*AN+ 0.09*AO+ 0.37*AP+ 0.17*AQ+ 0.28*AR+ 0.16*AS+ 0.16*AT+ 0.09*AU+ 0.1*AV+ 0.12*AW+ 0.09*AX+ 0*AY+ 0.51*AZ+ 0.51*BA+ 0.24*BB+ 0.09*BC+ 0.31*BD+ 0.18*BE+ 0*BF+ 0*BG+ 0.21*BH+ 0.2*BI+ 0.46*BJ+ 0.41*BK+ 0.45*BL+ 0*BM+ 0.08*BN+ 0.2*BO+ 0.35*BP+ 0.42*BQ+ 0.26*BR+ 0.35*BS+ 0.4*BT+ 0.14*BU+ 0.39*BV+ 0.22*BW+ 0.21*BX+ 0.14*BY+ 0.2*BZ+ 0.15*CA+ 0.35*CB+ 0.13*CC+ 0.23*CD+ 0.36*CE+ 0.37*CF+ 0.24*CG+ 0.32*CH+ 0.41*CI+ 0.06*CJ+ 0.01*CK+ 0.01*CL+ 0.01*CM+ 0.02*CN+ 0.07*CO+ 0.09*CP+ 0.01*CQ+ 0.09*CR+ 0.01*CS+ 0.08*CT+ 0.24*CU+ 0.2*CV+ 0.31*CW+ 0.1*CX+ 0.01*CY+ 0.01*CZ+ 0*DA+ 0*DB+ 0.03*DC+ 0*DD+ 0.24*DE+ 0.38*DF+ 0*DG+ 0.03*DH+ 0.03*DI+ 0.01*DJ+ 0.29*DK+ 0.3*DL+ 0.13*DM+ 0.23*DN+ 0.26*DO+ 0.23*DP+ 0*DQ+ 0.01*DR - 1.6) ** 2
con12 = (1*AA+ 3.3*AB+ 7.9*AC+ 2.3*AD+ 8.1*AE+ 3.6*AF+ 2.6*AG+ 1.2*AH+ 10.7*AI+ 3.9*AJ+ 4.8*AK+ 4.3*AL+ 6.2*AM+ 0*AN+ 5*AO+ 2.9*AP+ 2.9*AQ+ 4.1*AR+ 2.5*AS+ 5*AT+ 5.3*AU+ 5.6*AV+ 8.2*AW+ 2.5*AX+ 0*AY+ 3.9*AZ+ 3.9*BA+ 4.4*BB+ 1.4*BC+ 1.3*BD+ 2.6*BE+ 0*BF+ 0*BG+ 4.3*BH+ 4.2*BI+ 4.2*BJ+ 2.6*BK+ 5.4*BL+ 0*BM+ 1.3*BN+ 15.8*BO+ 6.6*BP+ 4.1*BQ+ 6.6*BR+ 7.5*BS+ 7*BT+ 9.5*BU+ 7.2*BV+ 4.1*BW+ 9.5*BX+ 9.8*BY+ 15.7*BZ+ 4*CA+ 7.5*CB+ 2.1*CC+ 4.1*CD+ 7.3*CE+ 6.4*CF+ 4.9*CG+ 3.6*CH+ 4.1*CI+ 1*CJ+ 0*CK+ 0.1*CL+ 0.3*CM+ 0.2*CN+ 12.5*CO+ 7.7*CP+ 0.1*CQ+ 7.6*CR+ 0*CS+ 7.6*CT+ 0.2*CU+ 0.2*CV+ 21.3*CW+ 7.1*CX+ 0*CY+ 0.9*CZ+ 0.2*DA+ 0*DB+ 0.8*DC+ 0.3*DD+ 20.5*DE+ 33.9*DF+ 0.1*DG+ 6.3*DH+ 5*DI+ 2.7*DJ+ 0.3*DK+ 0.6*DL+ 0.1*DM+ 0.4*DN+ 0.4*DO+ 0.3*DP+ 0.1*DQ+ 0.1*DR - 15) ** 2
con13 = (1*AA+ 1*AB+ 1*AC+ 6*AD+ 1*AE+ 1*AF+ 1*AG+ 0*AH+ 2*AI+ 6*AJ+ 17*AK+ 7*AL+ 2*AM+ 0*AN+ 1*AO+ 0*AP+ 0*AQ+ 1*AR+ 1*AS+ 1*AT+ 0*AU+ 0*AV+ 1*AW+ 1*AX+ 0*AY+ 1*AZ+ 1*BA+ 2*BB+ 0*BC+ 6*BD+ 7*BE+ 0*BF+ 0*BG+ 6*BH+ 0*BI+ 0*BJ+ 5*BK+ 6*BL+ 0*BM+ 1*BN+ 2*BO+ 2*BP+ 1*BQ+ 6*BR+ 17*BS+ 7*BT+ 1*BU+ 1*BV+ 1*BW+ 1*BX+ 0*BY+ 1*BZ+ 1*CA+ 2*CB+ 0*CC+ 7*CD+ 6*CE+ 0*CF+ 17*CG+ 1*CH+ 1*CI+ 8*CJ+ 5*CK+ 0*CL+ 19*CM+ 15*CN+ 40*CO+ 0*CP+ 0*CQ+ 0*CR+ 0*CS+ 0*CT+ 0*CU+ 0*CV+ 3*CW+ 1*CX+ 0*CY+ 1*CZ+ 1*DA+ 0*DB+ 0*DC+ 0*DD+ 22*DE+ 43*DF+ 0*DG+ 20*DH+ 16*DI+ 9*DJ+ 0*DK+ 0*DL+ 0*DM+ 3*DN+ 0*DO+ 0*DP+ 0*DQ+ 0*DR - 100) ** 2
con14 = (66*AA+ 56*AB+ 49*AC+ 47*AD+ 50*AE+ 56*AF+ 248*AG+ 231*AH+ 187*AI+ 49*AJ+ 73*AK+ 74*AL+ 109*AM+ 0*AN+ 37*AO+ 255*AP+ 45*AQ+ 76*AR+ 38*AS+ 50*AT+ 35*AU+ 35*AV+ 49*AW+ 26*AX+ 18*AY+ 478*AZ+ 458*BA+ 69*BB+ 40*BC+ 228*BD+ 47*BE+ 21*BF+ 0*BG+ 54*BH+ 30*BI+ 254*BJ+ 227*BK+ 294*BL+ 0*BM+ 126*BN+ 93*BO+ 105*BP+ 274*BQ+ 93*BR+ 118*BS+ 119*BT+ 69*BU+ 127*BV+ 64*BW+ 82*BX+ 66*BY+ 92*BZ+ 52*CA+ 121*CB+ 68*CC+ 73*CD+ 103*CE+ 113*CF+ 68*CG+ 79*CH+ 99*CI+ 0*CJ+ 0*CK+ 7*CL+ 0*CM+ 0*CN+ 23*CO+ 44*CP+ 1*CQ+ 43*CR+ 0*CS+ 43*CT+ 116*CU+ 12*CV+ 188*CW+ 63*CX+ 7*CY+ 4*CZ+ 0*DA+ 11*DB+ 5*DC+ 2*DD+ 136*DE+ 210*DF+ 2*DG+ 11*DH+ 9*DI+ 5*DJ+ 17*DK+ 17*DL+ 4*DM+ 14*DN+ 14*DO+ 14*DP+ 6*DQ+ 0*DR - 0) ** 2
con15 = (2.9*AA+ 0.8*AB+ 1.9*AC+ 0.9*AD+ 2.8*AE+ 1.7*AF+ 1.5*AG+ 1.7*AH+ 3.2*AI+ 2.3*AJ+ 2.4*AK+ 1.9*AL+ 3.2*AM+ 0.2*AN+ 2.2*AO+ 1.7*AP+ 1.7*AQ+ 1.7*AR+ 1.5*AS+ 2.2*AT+ 1.9*AU+ 2.5*AV+ 2.8*AW+ 1.5*AX+ 0*AY+ 6.1*AZ+ 3.2*BA+ 2.6*BB+ 2.1*BC+ 1.1*BD+ 1.7*BE+ 2.8*BF+ 0*BG+ 1.5*BH+ 1.6*BI+ 1.7*BJ+ 1.8*BK+ 2*BL+ 0*BM+ 3.9*BN+ 4*BO+ 1.8*BP+ 1.6*BQ+ 2.3*BR+ 2.5*BS+ 2*BT+ 2.9*BU+ 1.8*BV+ 1.6*BW+ 2.9*BX+ 2.5*BY+ 3.9*BZ+ 1.6*CA+ 2.7*CB+ 3*CC+ 1.8*CD+ 1.5*CE+ 1.8*CF+ 2.3*CG+ 1.7*CH+ 1.7*CI+ 2.9*CJ+ 0*CK+ 0.5*CL+ 0.4*CM+ 0.8*CN+ 12*CO+ 1.1*CP+ 0*CQ+ 1.2*CR+ 0.1*CS+ 1.1*CT+ 0.2*CU+ 0.3*CV+ 2.6*CW+ 0.9*CX+ 0.1*CY+ 1.5*CZ+ 0.3*DA+ 1.3*DB+ 2.3*DC+ 1*DD+ 7.7*DE+ 14.6*DF+ 0.3*DG+ 6*DH+ 4.8*DI+ 2.6*DJ+ 0.7*DK+ 1.7*DL+ 0.1*DM+ 1*DN+ 1.1*DO+ 0.7*DP+ 0.1*DQ+ 0.1*DR - 21) ** 2
con16 = (2.3*AA+ 2.5*AB+ 3.3*AC+ 2.5*AD+ 3.1*AE+ 2.1*AF+ 2.1*AG+ 1.6*AH+ 6*AI+ 2.1*AJ+ 2.7*AK+ 2.9*AL+ 4.4*AM+ 0*AN+ 2.5*AO+ 2*AP+ 1.8*AQ+ 2.9*AR+ 1.9*AS+ 2.7*AT+ 2.2*AU+ 2.1*AV+ 2.9*AW+ 1.4*AX+ 0.1*AY+ 4.2*AZ+ 2.4*BA+ 2.6*BB+ 1.6*BC+ 1.6*BD+ 2.1*BE+ 1.8*BF+ 0*BG+ 2.3*BH+ 2.5*BI+ 3*BJ+ 2.6*BK+ 3.4*BL+ 0.6*BM+ 3.3*BN+ 5.3*BO+ 3.3*BP+ 2.4*BQ+ 2.5*BR+ 3.1*BS+ 3.3*BT+ 3.8*BU+ 3.6*BV+ 2.3*BW+ 4*BX+ 3.4*BY+ 4.5*BZ+ 1.8*CA+ 3.3*CB+ 2.1*CC+ 2.5*CD+ 2.9*CE+ 3.6*CF+ 3.4*CG+ 3.2*CH+ 3*CI+ 0.2*CJ+ 0*CK+ 0.6*CL+ 0.5*CM+ 0*CN+ 2.1*CO+ 2*CP+ 0.4*CQ+ 1.9*CR+ 0.2*CS+ 1.6*CT+ 0.1*CU+ 0.2*CV+ 3.9*CW+ 1.3*CX+ 0.7*CY+ 0.8*CZ+ 0.5*DA+ 0.8*DB+ 0.4*DC+ 0.6*DD+ 3.6*DE+ 6*DF+ 0.5*DG+ 1.1*DH+ 0.8*DI+ 0.5*DJ+ 0.4*DK+ 0.7*DL+ 0.1*DM+ 0.3*DN+ 0.3*DO+ 0.3*DP+ 0.6*DQ+ 1*DR - 5) ** 2

# 最後にペナルティを定義してQUBO形式の目的関数化
A = Placeholder("A")
H = obj + A * (con1 + con2 + con3 + con4 + con5 + con6 + con7 + con8 + con9 + con10 + con11 + con12 + con13 + con15 + con16)

model = H.compile()

# QUBOのモデル化（ペナルティを1300に定義する）
qubo, offset = model.to_qubo(feed_dict={'A': 1300.0})

value_array = ["AA", "AB", "AC", "AD", "AE", "AF", "AG", "AH", "AI", "AJ", "AK", "AL", "AM", "AN", "AO", "AP", "AQ", "AR", "AS", "AT", "AU", "AV", "AW", "AX", "AY", "AZ", "BA", "BB", "BC", "BD", "BE", "BF", "BG", "BH", "BI", "BJ", "BK", "BL", "BM", "BN", "BO", "BP", "BQ", "BR", "BS", "BT", "BU", "BV", "BW", "BX", "BY", "BZ", "CA", "CB", "CC", "CD", "CE", "CF", "CG", "CH", "CI", "CJ", "CK", "CL", "CM", "CN", "CO", "CP", "CQ", "CR", "CS", "CT", "CU", "CV", "CW", "CX", "CY", "CZ", "DA", "DB", "DC", "DD", "DE", "DF", "DG", "DH", "DI", "DJ", "DK", "DL", "DM", "DN", "DO", "DP", "DQ", "DR"]

# D-Waveで使用できるように整数タプルの辞書型に変更
Q = {}
for i in range(len(value_array)):
    for j in range(len(value_array)):
        if((value_array[i], value_array[j]) in qubo):
            Q[(i, j)] = qubo[value_array[i], value_array[j]]

D-Waveの変数定義と実行

AmazonBraket上のD-Waveでは、いくつかの変数を定義する必要があるので定義していきます。
細かい説明はあまりしない想定なのでぜひドキュメントを読んでいただけると幸いです。

D-Waveの変数定義（chainstrengthはquboの最大値としました。）
import も一緒にしておきます。

from braket.ocean_plugin import BraketDWaveSampler
from dwave.system.composites import EmbeddingComposite
chainstrength = max(qubo.values())
numruns = 10000  

AmazonBraket特有のS3の定義
(AmazonBraketでは結果を格納するS3の定義をする必要があるため、定義します。)

# Please enter the S3 bucket you created during onboarding in the code below
my_bucket = "amazon-braket-Your-Bucket-Name" # the name of the bucket
my_prefix = "Your-Folder-Name" # the name of the folder in the bucket
s3_folder = (my_bucket, my_prefix)

実行します。

sampler = EmbeddingComposite(BraketDWaveSampler(s3_folder,'arn:aws:braket:::device/qpu/d-wave/Advantage_system1'))
sampler = EmbeddingComposite(sampler)
response = sampler.sample_qubo(Q, chain_strength=chainstrength, num_reads=numruns)

結果

結果を表示します．．．。

ValueError: no embedding found

．．．。
まあ、そうなりますよね。。。
簡単に説明すると上記のエラーは変数を量子ビットに割り当てきれなかったときに出るようなエラーです。
D-Waveは今のところ量子ビットにすると5760量子ビットを扱うことができるわけですがこれを古典ビットとマッピングすると意外に使えるビット数は少ないんですよね。。。。
今回は100近くの変数だったのでまあまあきつかったようです。。。

まあだから求まらなかったのですが、、、
ここまで書いたし、しかもここまで読んでいただいた方に申し訳ないのでウルトラCとして別案をやってみます。

それでもあきらめない！

最近こんなSDKが誕生しました。
Fixstars Amplify
というあらゆるイジングマシンに対応したアプリケーション開発を実現するためのクラウドプラットフォームです。
これを利用してD-Waveを利用することもできるのですが、なんとこちらのツール、量子コンピュータではありませんが、
最大ビット数100,000以上のイジングマシンを利用できます。
一応、前述したQUBO形式の最適化問題はイジングマシンで解くことができるのですが、イジングマシンは量子であっても、GPUベースであっても、デジタル回路であっても問題はありません。

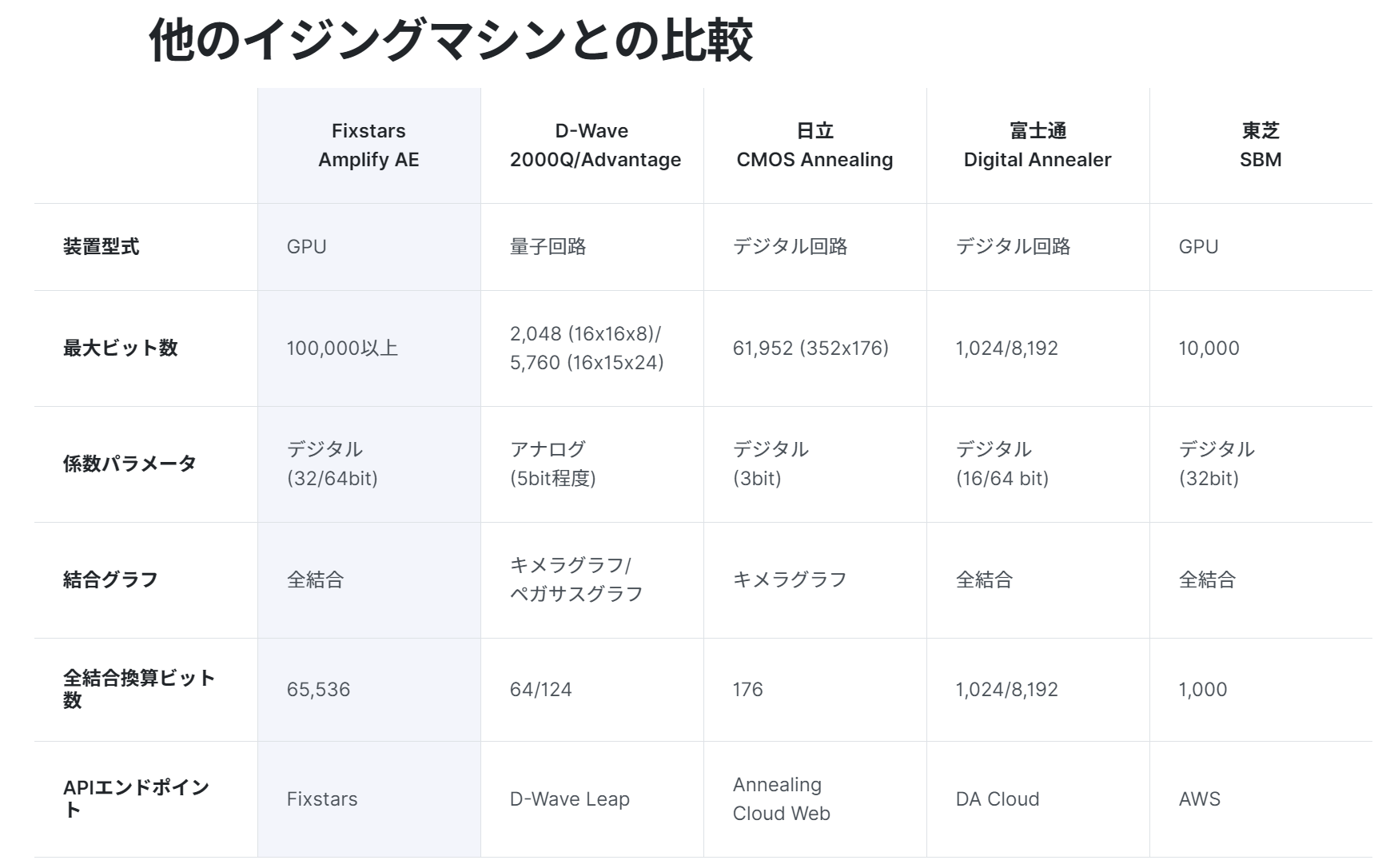
引用：https://amplify.fixstars.com/engine

イジングモデル（QUBOモデル）をハードウェアで解きやすくしているのが上記マシンのセットであり、こうやってイジングモデル（QUBOモデル）が解きやすくなることは最適化がより身近になってきた感じがするのでうれしい限りです。

ということで「Fixstars Amplify AE」で解きましょう。

まずはユーザ登録

こちらの無料ユーザ登録画面よりユーザ登録を行ってください。
ユーザ登録をして少し時間がたつとアクセストークンが発行されるのでアクセストークンを大事に保管しておいてください。
後で使います。

インストール

困ったときのpipです。
それだけでインストールできます。
もしかしたらwindowsマシンにはインストールできないかもしれません。定かではない。。。。
とりあえず私はAWS SageMaker上にインストールしました。

pip install amplify

定式化

D-Waveと定式化は一緒なので省略します。
以下の部分まで実行して入れば続きでできます。

# D-Waveで使用できるように整数タプルの辞書型に変更
Q = {}
for i in range(len(value_array)):
    for j in range(len(value_array)):
        if((value_array[i], value_array[j]) in qubo):
            Q[(i, j)] = qubo[value_array[i], value_array[j]]

Amplifyのモデル定義

Amplify では以下のようにモデルを定義します。
import もとりあえず以下のようにimportしていれば大丈夫です。

from amplify import (
    BinaryPoly,
    BinaryQuadraticModel,
    gen_symbols,
    Solver,
    decode_solution,
)
from amplify.client import FixstarsClient


model = BinaryPoly(Q)

Amplifyの実行

では、Amplifyの実行をしていきます。
上記で取得したトークンの設定を忘れずに行ってください。

client = FixstarsClient()
client.token = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxx" # 取得したトークンの設定
client.parameters.timeout = 1000    # タイムアウト1秒

solver = Solver(client)
result = solver.solve(model)
for solution in result:
    print(f"energy = {solution.energy}\nvalues = {solution.values}")

結果は以下のようになります。

energy = -11873929762.39
values = {56: 0, 11: 0, 70: 0, 19: 0, 78: 0, 39: 0, 18: 0, 77: 0, 8: 0, 16: 0, 58: 0, 13: 0, 14: 0, 73: 1, 20: 0, 87: 0, 95: 0, 36: 0, 84: 0, 64: 0, 32: 0, 3: 0, 52: 0, 22: 0, 81: 0, 55: 0, 37: 0, 21: 0, 1: 0, 60: 0, 65: 1, 6: 0, 34: 0, 93: 0, 94: 0, 35: 0, 54: 0, 40: 0, 43: 0, 38: 0, 45: 0, 46: 0, 66: 0, 7: 0, 88: 0, 89: 0, 30: 0, 44: 0, 74: 0, 15: 0, 26: 0, 85: 1, 41: 0, 57: 0, 76: 0, 63: 0, 4: 0, 42: 0, 53: 0, 75: 0, 67: 0, 27: 0, 68: 0, 49: 0, 79: 0, 72: 1, 91: 0, 69: 0, 48: 0, 86: 1, 9: 0, 25: 0, 24: 0, 33: 0, 82: 0, 62: 1, 28: 0, 51: 0, 92: 0, 59: 0, 23: 0, 29: 0, 90: 1, 50: 0, 2: 0, 47: 0, 10: 0, 31: 0, 61: 0, 17: 0, 5: 0, 12: 0, 71: 0, 0: 0, 80: 0, 83: 0}

各変数のインデックスを整数にしたので少しわかりにくくなっています。

結果の復元

上記ではやや結果がわかりにくいので復元します。

name = ["えびフィレオ:", "ごはんてりやき:", "ごはんチキンフィレオ:", "ごはんベーコンレタス:", "てりやきチキンフィレオ:", "てりやきマックバーガー:", "エグチ(エッグチーズバーガー):", "エッグマックマフィン:", "ギガビッグマック®:", "グラン ガーリックペッパー:", "グラン クラブハウス:", "グラン ベーコンチーズ:", "グランドビッグマック®:", "ストロベリージャム:", "スパチキ(スパイシーチキンバーガー):", "ソーセージエッグマフィン:", "ソーセージマフィン:", "ダブルチーズバーガー:", "チーズバーガー:", "チキチー(チキンチーズバーガー):", "チキンクリスプ:", "チキンクリスプマフィン:", "チキンフィレオ:", "ハンバーガー:", "バターパット:", "ビッグブレックファスト デラックス(ハッシュポテト含む):", "ビッグブレックファスト(ハッシュポテト含む):", "ビッグマック®:", "フィレオフィッシュ:", "ベーコンエッグマックサンド:", "ベーコンレタスバーガー:", "ホットケーキ:", "ホットケーキシロップ:", "マクポ(ベーコンマックポーク):", "マックグリドル ソーセージ:", "マックグリドル ソーセージエッグ:", "マックグリドル ベーコンエッグ:", "メガマフィン:", "塩・コショウ:", "倍えびフィレオ:", "倍てりやきチキンフィレオ:", "倍てりやきマックバーガー:", "倍エグチ(倍エッグチーズバーガー):", "倍グラン ガーリックペッパー:", "倍グラン クラブハウス:", "倍グラン ベーコンチーズ:", "倍スパチキ(倍スパイシーチキンバーガー):", "倍ダブルチーズバーガー:", "倍チーズバーガー:", "倍チキチー(倍チキンチーズバーガー):", "倍チキンクリスプ:", "倍チキンフィレオ:", "倍ハンバーガー:", "倍ビッグマック®:", "倍フィレオフィッシュ:", "倍ベーコンレタスバーガー:", "倍マクポ(倍ベーコンマックポーク):", "炙り醤油風 ダブル肉厚ビーフ:", "炙り醤油風 ベーコントマト肉厚ビーフ:", "チーズチーズてりやきマックバーガー:", "チーズチーズダブルチーズバーガー:", "えだまめコーン:", "りんご&クリーム:", "クリームブリュレパイ:", "ケチャップ:", "サイドサラダ:", "シェアポテト:", "シャカチキ チェダーチーズ:", "シャカチキ チェダーチーズ味シーズニング:", "シャカチキ レッドペッパー:", "シャカチキ レッドペッパー味シーズニング:", "シャカチキ(チキンのみ):", "スジャータアイスバニラ:", "ソフトツイスト:", "チキンマックナゲット 15ピース:", "チキンマックナゲット 5ピース:", "トリュフ香るパルメザンチーズソース:", "ハッシュポテト:", "バーベキューソース:", "プチパンケーキ:", "ベルギーショコラパイ:", "ホットアップルパイ:", "ポテナゲ大:", "ポテナゲ特大:", "マスタードソース:", "マックフライポテト(L):", "マックフライポテト(M):", "マックフライポテト(S):", "マックフルーリー® オレオ®クッキー:", "マックフルーリー® 超 オレオ®:", "ヨーグルト:", "ワッフルコーン ストロベリー:", "ワッフルコーン チョコ&アーモンド:", "ワッフルコーン プレーン:", "伊勢海老と紅ズワイガニソース:", "低カロリー玉ねぎ:"]
for solution in result:
    for i in range(len(value_array)):
        print(value_array[i] + ": " + name[i] + " " + str(solution.values[i]))

AA: えびフィレオ: 0
AB: ごはんてりやき: 0
AC: ごはんチキンフィレオ: 0
AD: ごはんベーコンレタス: 0
AE: てりやきチキンフィレオ: 0
AF: てりやきマックバーガー: 0
AG: エグチ(エッグチーズバーガー): 0
AH: エッグマックマフィン: 0
AI: ギガビッグマック®: 0
AJ: グラン ガーリックペッパー: 0
AK: グラン クラブハウス: 0
AL: グラン ベーコンチーズ: 0
AM: グランドビッグマック®: 0
AN: ストロベリージャム: 0
AO: スパチキ(スパイシーチキンバーガー): 0
AP: ソーセージエッグマフィン: 0
AQ: ソーセージマフィン: 0
AR: ダブルチーズバーガー: 0
AS: チーズバーガー: 0
AT: チキチー(チキンチーズバーガー): 0
AU: チキンクリスプ: 0
AV: チキンクリスプマフィン: 0
AW: チキンフィレオ: 0
AX: ハンバーガー: 0
AY: バターパット: 0
AZ: ビッグブレックファスト デラックス(ハッシュポテト含む): 0
BA: ビッグブレックファスト(ハッシュポテト含む): 0
BB: ビッグマック®: 0
BC: フィレオフィッシュ: 0
BD: ベーコンエッグマックサンド: 0
BE: ベーコンレタスバーガー: 0
BF: ホットケーキ: 0
BG: ホットケーキシロップ: 0
BH: マクポ(ベーコンマックポーク): 0
BI: マックグリドル ソーセージ: 0
BJ: マックグリドル ソーセージエッグ: 0
BK: マックグリドル ベーコンエッグ: 0
BL: メガマフィン: 0
BM: 塩・コショウ: 0
BN: 倍えびフィレオ: 0
BO: 倍てりやきチキンフィレオ: 0
BP: 倍てりやきマックバーガー: 0
BQ: 倍エグチ(倍エッグチーズバーガー): 0
BR: 倍グラン ガーリックペッパー: 0
BS: 倍グラン クラブハウス: 0
BT: 倍グラン ベーコンチーズ: 0
BU: 倍スパチキ(倍スパイシーチキンバーガー): 0
BV: 倍ダブルチーズバーガー: 0
BW: 倍チーズバーガー: 0
BX: 倍チキチー(倍チキンチーズバーガー): 0
BY: 倍チキンクリスプ: 0
BZ: 倍チキンフィレオ: 0
CA: 倍ハンバーガー: 0
CB: 倍ビッグマック®: 0
CC: 倍フィレオフィッシュ: 0
CD: 倍ベーコンレタスバーガー: 0
CE: 倍マクポ(倍ベーコンマックポーク): 0
CF: 炙り醤油風 ダブル肉厚ビーフ: 0
CG: 炙り醤油風 ベーコントマト肉厚ビーフ: 0
CH: チーズチーズてりやきマックバーガー: 0
CI: チーズチーズダブルチーズバーガー: 0
CJ: えだまめコーン: 0
CK: りんご&クリーム: 1
CL: クリームブリュレパイ: 0
CM: ケチャップ: 0
CN: サイドサラダ: 1
CO: シェアポテト: 0
CP: シャカチキ チェダーチーズ: 0
CQ: シャカチキ チェダーチーズ味シーズニング: 0
CR: シャカチキ レッドペッパー: 0
CS: シャカチキ レッドペッパー味シーズニング: 0
CT: シャカチキ(チキンのみ): 0
CU: スジャータアイスバニラ: 1
CV: ソフトツイスト: 1
CW: チキンマックナゲット 15ピース: 0
CX: チキンマックナゲット 5ピース: 0
CY: トリュフ香るパルメザンチーズソース: 0
CZ: ハッシュポテト: 0
DA: バーベキューソース: 0
DB: プチパンケーキ: 0
DC: ベルギーショコラパイ: 0
DD: ホットアップルパイ: 0
DE: ポテナゲ大: 0
DF: ポテナゲ特大: 0
DG: マスタードソース: 0
DH: マックフライポテト(L): 1
DI: マックフライポテト(M): 1
DJ: マックフライポテト(S): 0
DK: マックフルーリー® オレオ®クッキー: 0
DL: マックフルーリー® 超 オレオ®: 0
DM: ヨーグルト: 1
DN: ワッフルコーン ストロベリー: 0
DO: ワッフルコーン チョコ&アーモンド: 0
DP: ワッフルコーン プレーン: 0
DQ: 伊勢海老と紅ズワイガニソース: 0
DR: 低カロリー玉ねぎ: 0

これでもわかりづらいので1となっている商品だけ表示します。

for solution in result:
    for i in range(len(value_array)):
        if(solution.values[i] == 1):
            print(value_array[i] + ": " + name[i] + " " + str(solution.values[i]))

CK: りんご&クリーム: 1
CN: サイドサラダ: 1
CU: スジャータアイスバニラ: 1
CV: ソフトツイスト: 1
DH: マックフライポテト(L): 1
DI: マックフライポテト(M): 1
DM: ヨーグルト: 1

なかなか健康かな～とおもいつつ、マックフライポテト(L), (M)が両方含まれてしまいました。

そして再度サラダが．．．。
最適化民はサイドサラダ好きなんですね笑笑笑

一つだけの制約にしておいてよかった気がします笑

ちなみにカロリーを（ほぼ手動で）復元すると

objective = 31 + 10 + 275+ 148+ 517 + 410 + 59  
# CK: りんご&クリーム(31) + CN: サイドサラダ(10) + CU: スジャータアイスバニラ(275) + CV: ソフトツイスト(148) + DH: マックフライポテト(L)(517) + DI: マックフライポテト(M)(410) + DM: ヨーグルト(59)
objective

1450

1450kcalとなるそうです。
なんか思ったより小さくなったぞ笑

量子コンピュータでサイドサラダ王にはなれなかった

今回は以下の記事を参考にしてみました。
https://qiita.com/takobaya391076/items/49b15c1fa36734b3fa53
上記記事では0, 1という縛りもなくやっているため、サイドサラダ王になれたそうですが、量子コンピュータで実行すると変数が増えちゃってサイドサラダ王になれないんですよね。
他にも制約がかけづらかったり。。。
とはいえ、まだまだ発展途上なのでハードウェア的にアップデートあればまた結果は変わってくるのではないかとも思います。
ペナルティも割と適当においてますしね。
結構サクッと定式化とかしちゃったのでもっと考えれば良い感じの結果になった気もします。
とはいえ、マックフライポテト(L), (M)もなかなかな結果ですし、スジャータアイスバニラって何なんですかね笑

以上で～～～す！