量子回路学習 QCL: Quantum Circuit Learning をさらっと実装してみた

この記事について

本記事では、量子コンピュータで機械学習を行うために用いられる量子回路学習（Quantum Circuit Learning）というアルゴリズムをさらっと解説をしていこうと思います。多くの書籍や記事では、数学的背景等も一緒に述べているものが多く、QCLをとりあえず使いたい。といったユーザに対しては少し情報が多めになっており、わかりづらいということもあるかと思います。本記事はそういった方のために、数学的背景はまず置いておいて、まず使おうといった趣旨で書かせていただきます。

量子コンピュータ関係の他の記事は、下記で紹介しています。

概要

VQEやQAOAではエネルギー期待値を最小化するようにパラメータ付き量子回路のパラメータを最適化することにより、所望の結果を求めることができます。量子回路学習（QCL）はこれを拡張し、パラメータ付き量子回路の出力と訓練出力の差を最小化するようにパラメータの最適化を行います。

QCLを用いた学習はニューラルネットワークによる学習と似ています。ニューラルネットワークはパラメータを持つ線形変換と非線形関数を用いてパラメータ最適化によって教師データと突き合わせることにより出力を近似させます。量子回路学習では量子回路のテンソル積構造を用いることで出力を近似します。つまり、ニューラルネットワークの各層に隠れている重み付きパラメータが量子回路に含まれる複数の回転ゲートのパラメータに対応します。

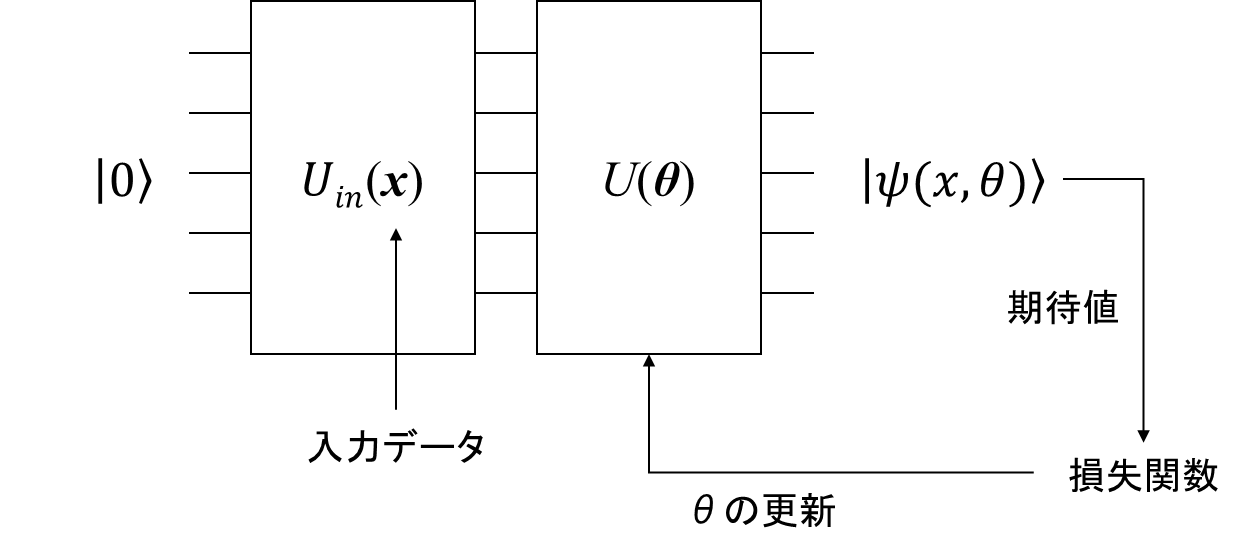
以下の図で簡単に説明すると、インプットデータを $U_{in}(x) $でエンコードし、$U(\theta) $で示されるパラメータ付き回路（回転ゲート）を用いることで出力を得ます。$U(\theta) $はパラメータ付き回路なので出力される値（期待値）を用いて損失関数を計算し、学習の情報を獲得し、次の$\theta$の更新に適用します。

手順

入力データ$x_i$、$x_i$から予測したい正解データ（教師データ）$y_i$が与えられているとき、以下の手順でQCLのフローとなります。

1. $U_{\text{in}}(x)$という、入力$x$から決まるある回路（とりあえずなんでも良い）を用意し、$x_i$の情報を埋め込んだ入力の状態 ${|\psi_{in}(x_i)\rangle}$ を作る
2. 入力状態にパラメータ$\theta$に依存したゲート$U(\theta)$をかけたものを出力状態${|\psi_{\rm out}(x_i, \theta)\rangle = U(\theta)|\psi_{\rm in}(x_i)\rangle }$とする
3. 出力状態を測定し、測定値を得る（例：1番目のqubitの$Z$の期待値$\langle Z_1\rangle = \langle \psi_{\rm out} |Z_1|\psi_{\rm out} \rangle$）
4. 関数 $f(x)$ （定義域、地域が合うように定義された関数、ソフトマックスやシグモイド、定数倍等）で最終的なモデル出力 ${y_i}$に変換する
5. 正解データ${y_i}$とモデルの出力${y(x_i, \theta)}_i$の間の乖離を表す「コスト関数$L(\theta)$」を計算し、コスト関数を最小化する$\theta=\theta^*$を求める
6. 所望のモデル $y(x, \theta^*)$ を得る。

（参考：Quantum Native Dojo）

未知のデータ$\tilde{x}$を予測したい時は$U_{in}(\tilde{x})$でエンコードし、上記で獲得された $\theta^* $ を使った $U(\theta^* )$ を実行して、予測値 $y(\tilde{x}, \theta^* )$を取得します。

例

具体的な回路を2量子ビットの量子回路を用いて見てみます。
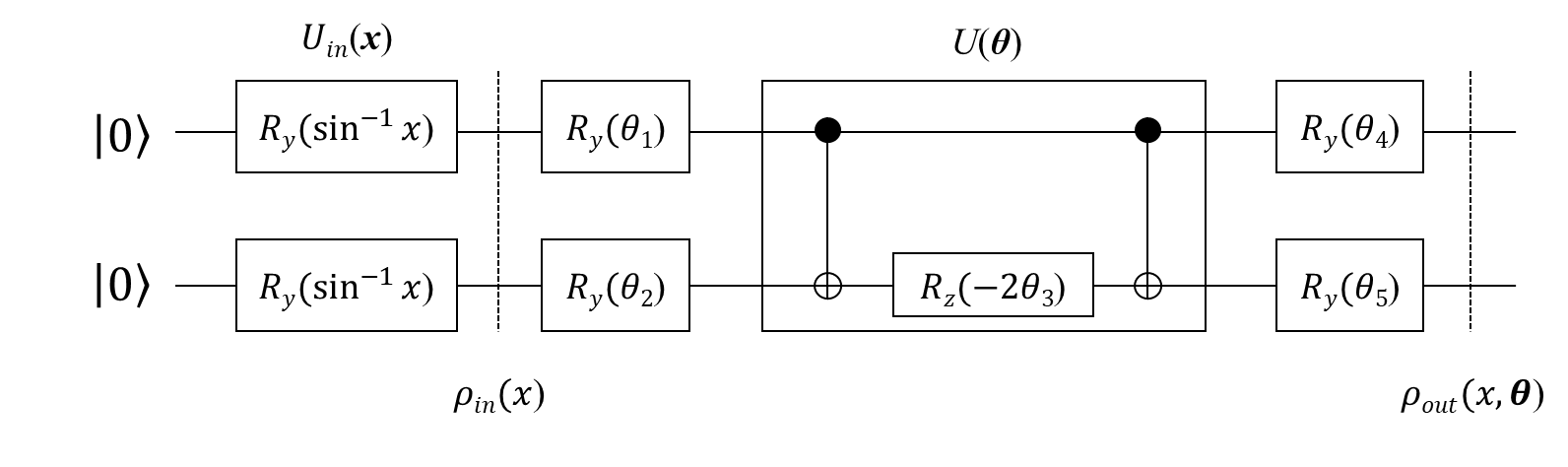
例えば1次元のデータ$x$に対して線形となるような $2sin^{-1}x$を引数とするY軸回転ゲートを$U_{\text{in}}(x)$をインプットのエンコードとして使用すると、以下のように簡単に量子回路を示すことができます。

これも立派な量子回路学習の回路で実際にこの回路図は「量子コンピューティング 基本アルゴリズムから量子機械学習まで」で紹介されています。「量子コンピューティング 基本アルゴリズムから量子機械学習まで」では、$2sin^{-1}x$を引数とするY軸回転ゲートが数学的にどう重要なのかも記載されているので興味ある方は是非見てみてください。
$U(\theta)$ の回路もそれなりに意味のあるものにはなっていますが、私の感覚としては意外といろんな回路が使えそうです。実際に上記の書籍では、様々な量子回路が紹介されていたり、最近よく開催されている量子アルゴリズムコンテスト等では量子回路学習における効率的な回路設計がテーマになっていたりすることもあります。

実験

では、実際に量子回路学習やってみましょ～。
ぶっちゃけ、こちらのQuantum Native Dojoやこちらの記事にやり方が書いてるので、今回は Quantum Native Dojoを見ながら少し独自性を出していこうと思います。上記でも示した以下の回路を用いて量子回路学習を実践していきます。（なのでちゃんとした解説を見たい方はQuantum Native Dojoも見てみてると良いと思います。）

問題の定義

問題の定義はQuantum Native Dojoに記載されているものと同じものを用いていこうと思います。つまり、sinxの関数近似をしていこうと思います。
Quantum Native Dojoと同じようにsinxにノイズを加えた教師データを用意します。

import numpy as np
import matplotlib.pyplot as plt
from functools import reduce

## [x_min, x_max]のうち, ランダムにnum_x_train個の点をとって教師データとする.
x_min = - 1.; x_max = 1.;
num_x_train = 50

## 学習したい1変数関数
func_to_learn = lambda x: np.sin(x*np.pi)

## 乱数
random_seed = 0
np.random.seed(random_seed)

#### 教師データ
x_train = x_min + (x_max - x_min) * np.random.rand(num_x_train)
y_train = func_to_learn(x_train)

# sin関数にノイズを付加
mag_noise = 0.05
y_train = y_train + mag_noise * np.random.randn(num_x_train)

plt.plot(x_train, y_train, "o"); plt.show()

出力はこんな感じ

Qulacsのインストール

この実験はローカルのJupyter Notebookでやっているので環境に合わせてQulacsをインストールしておきます。

!pip install qulacs

初期状態の定義

今回は2量子ビットの回路を定義します。※Quantum Native Dojoは3量子ビットで定義されているので異なります。

from qulacs import QuantumState, QuantumCircuit
########  パラメータ  #############
nqubit = 2 ## qubitの数
state = QuantumState(nqubit) # 初期状態 |00>
state.set_zero_state()
print(state.get_vector())

エンコードの定義

$U_{in}(x)$を定義します。今回はあくまで上記の図の回路を定義して量子回路学習を行いたいのでここでは$sin(x)$の逆関数を入力とするY回転ゲートを定義します。

# xをエンコードするゲートを作成する関数
def U_in(x):
    U = QuantumCircuit(nqubit)

    angle_y = np.arcsin(x)

    for i in range(nqubit):
        U.add_RY_gate(i, angle_y)
    return U

学習回路の定義

$U(\theta)$を定義します。くどいですが、今回はあくまで上記の図の回路を定義します。
なので以下のように個別に一つずつ定義していきます。

from qulacs import ParametricQuantumCircuit
U_out = ParametricQuantumCircuit(nqubit)

angle = 2.0 * np.pi * np.random.rand()
U_out.add_parametric_RY_gate(0,angle)
angle = 2.0 * np.pi * np.random.rand()
U_out.add_parametric_RY_gate(1,angle)

U_out.add_CNOT_gate(0,1)
angle = 2.0 * np.pi * np.random.rand()
U_out.add_parametric_RZ_gate(1,-2 * angle)
U_out.add_CNOT_gate(0,1)

angle = 2.0 * np.pi * np.random.rand()
U_out.add_parametric_RY_gate(0,angle)
angle = 2.0 * np.pi * np.random.rand()
U_out.add_parametric_RY_gate(1,angle)

パラメータの初期値リストの取得と更新関数の定義

このあたりから、Quantum Native Dojoとあまり変わらない実装になるので、もしすでに読まれていて学習されている方はしばらく読み飛ばしても問題ありません。最後のおちへGoしてください！
という背景もあるのでなるべく簡易的な説明で以下は書いていきます。

後々、最適化させるためにパラメータの初期値を取得しておく必要があります。なのでこちらでパラメータの初期値を取得しておきます。

# パラメータthetaの初期値のリストを取得しておく
parameter_count = U_out.get_parameter_count()
theta_init = [U_out.get_parameter(ind) for ind in range(parameter_count)]
theta_init

出力はこんな感じ

[5.536134662197809,
 3.652245172807698,
 -11.080213340854174,
 4.351304311534335,
 4.556907034931878]

パラメータを更新する関数は以下の通りに定義します。

# パラメータthetaを更新する関数
def set_U_out(theta):
    global U_out

    parameter_count = U_out.get_parameter_count()

    for i in range(parameter_count):
        U_out.set_parameter(i, theta[i])

測定する計算基底の定義

今回はZ基底で測定するので以下の通り定義します。

# オブザーバブルZ_0を作成
from qulacs import Observable
obs = Observable(nqubit)
obs.add_operator(2.,'Z 0') 

予測値の取得とコスト関数の定義

# 入力x_iからモデルの予測値y(x_i, theta)を返す関数
def qcl_pred(x, U_out):
    state = QuantumState(nqubit)
    state.set_zero_state()

    # 入力状態計算
    U_in(x).update_quantum_state(state)

    # 出力状態計算
    U_out.update_quantum_state(state)

    # モデルの出力
    res = obs.get_expectation_value(state)

    return res

# cost function Lを計算
def cost_func(theta):
    '''
    theta: 長さc_depth * nqubit * 3のndarray
    '''
    # U_outのパラメータthetaを更新
#     global U_out
    set_U_out(theta)

    # num_x_train個のデータについて計算
    y_pred = [qcl_pred(x, U_out) for x in x_train]

    # quadratic loss
    L = ((y_pred - y_train)**2).mean()

    return L

初期状態

ここで初期状態を見てみます。
初期状態を可視化してみます。

# パラメータthetaの初期値のもとでのグラフ
xlist = np.arange(x_min, x_max, 0.02)
y_init = [qcl_pred(x, U_out) for x in xlist]
plt.plot(xlist, y_init)

何とも言えない感じ。。。笑
まあ初期状態だから仕方ないでしょう。。。
ここからどう学習してどのような解を得られるかが重要となります。

学習（最適化）

参考にしたQuantum Native Dojoと同じように scipy.optimize.minimizeを使って最適化していきます。

from scipy.optimize import minimize
result = minimize(cost_func, theta_init, method='Nelder-Mead')
# 最適化後のcost_functionの値
result.fun

出力として、0.18550728036269387が得られました。
あまり最適化されてない。。。？笑
やや不安な思いも抱えながら、可視化してみます。

可視化

以下の通り、こちらもQuantumNativeDojoに書かれているコードをそのまま使っています。

theta_opt = result.x
set_U_out(theta_opt)
# プロット
plt.figure(figsize=(10, 6))

xlist = np.arange(x_min, x_max, 0.02)

# 教師データ
plt.plot(x_train, y_train, "o", label='Teacher')

# パラメータθの初期値のもとでのグラフ
plt.plot(xlist, y_init, '--', label='Initial Model Prediction', c='gray')

# モデルの予測値
y_pred = np.array([qcl_pred(x, U_out) for x in xlist])
plt.plot(xlist, y_pred, label='Final Model Prediction')

plt.legend()
plt.show()

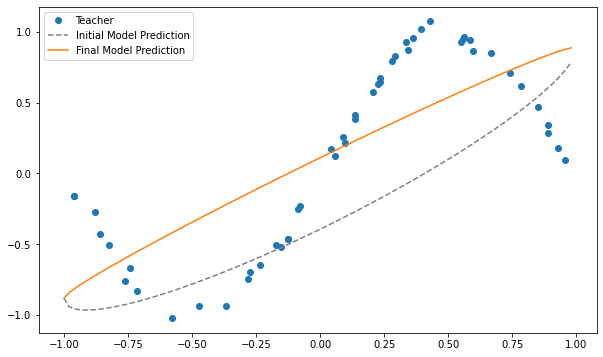
．．．。ということで全然最適化されてませんね笑

2量子ビットで定義した以下の回路だとこの問題は結構厳しかったということがわかりました笑

おまけ

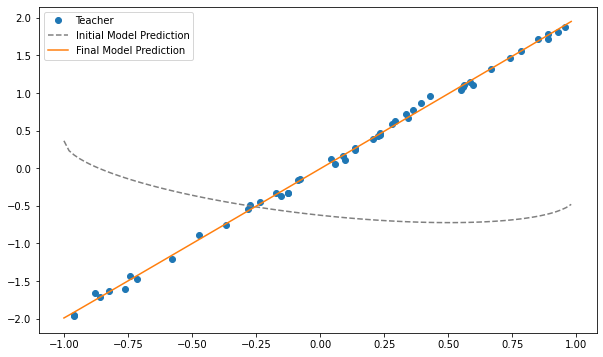
上記だとあまりにもかわいそうなので $y = 2x$の式の近似を行ってみました。
結果だけ示しますが、以下のようにかなり近似できていることがわかります。

こんな感じで量子回路学習で近似することができます。

ちなみに、、、
$y = sin(x)$ の近似を以下のように1量子ビットのZ回転ゲートを加えてみると、、、

まあまあ結果が改善します。

QAOAの線形項の追加みたいなものでしょうかね。（参考: QAOAの回路を丁寧に計算しながら作る話）
こういった形で少しの変化で結果が大きく変わるのでいろんな回路を構築してみるのも面白いと思います。
ということで何となく雰囲気が伝わったかな。。。と思います。

最後に

最近では結構量子アルゴリズム等の参考文献やSDKも整理されてきていてちょっと調べるだけで様々な実装を行うことができるようになりました。
今回の実装も文献でいうとQuantum Native Dojoを参考にさせていただき、Qulacsを使うことで簡単に実装できました。実際に変更したところは$U_{in}(x)$, $U(x)$の部分だけだったこともこの記事を読んでいただいた方にはわかっていただけると思います。
是非、はじめましての方もこういった文献を読んで手軽に量子回路を実装いただければと思います。
また、今回の記事はさらっと試しにQCLを実装してみた記事になっているので数学的な背景等は結構無視してしまっています。（なので結果もちゃんと出ていません笑）もし有識者の方がいれば是非、「ここでこうすると良い結果を得られるよ～」とか、「こういう背景を踏まえてやるとうまくいくよ。」、「元の文献だとこういうところに気を使ってやっているはずだ」等のコメントがあれば泣いて喜びます。
最後まで読んでいただきありがとうございます。