ΔΣ（デルタシグマ）変調のシミュレーション

1. 実験の狙いと基本設定

ΔΣ変調の最大の特徴は、量子化雑音を高い周波数帯域へ押しやる**「ノイズシェーピング」**にあります。本実験では、以下の設定で1次と2次の性能差を可視化します。

• サンプリング周波数 (fs_high): 512,000 Hz（高レート動作）
• デシメーション比 (OSR): 64
• 信号帯域 (BW): fs_low / 2 = 4,000 Hz
• 評価手法: Welch法による高分解能PSD（電力スペクトル密度）と帯域内SNR評価

2. アナログ信号の簡易モデル化

シミュレーション精度を高めるため、入力信号には実環境に近い「帯域制限」と「ディザ」を適用します。

• 入力信号: 1 kHzの正弦波（振幅 0.5）
• 2次Butterworth LPF: 入力信号をBW（4 kHz）以下に整形
• TPDFディザ: 三角確率密度関数（TPDF）を用いた微小ノイズを加え、量子化誤差と信号の相関を断ち切ることで、特定の周期雑音（アイドルトーン）を抑制

3. ΔΣモジュレータの離散時間ループ実装

1ビット量子化（±1）と積分器を組み合わせたループ処理の実装です。

(1) 1次ΔΣモジュレータ

積分器を1つ持ち、量子化誤差を1サンプル遅延させてフィードバックします。

• v1[n] = leak * v1[n-1] + (x[n] - y[n-1])
• y[n] = sign(v1[n])

(2) 2次ΔΣモジュレータ

積分器を2個直列に配置することで、より強力にノイズを押し上げます。

• v1[n] = leak * v1[n-1] + (x[n] - y[n-1])
• v2[n] = leak * v2[n-1] + (v1[n] - y[n-1])
• y[n] = sign(v2[n])
  ※leak（0.99999）は数値的な発散を抑えるための微小な減衰係数です。

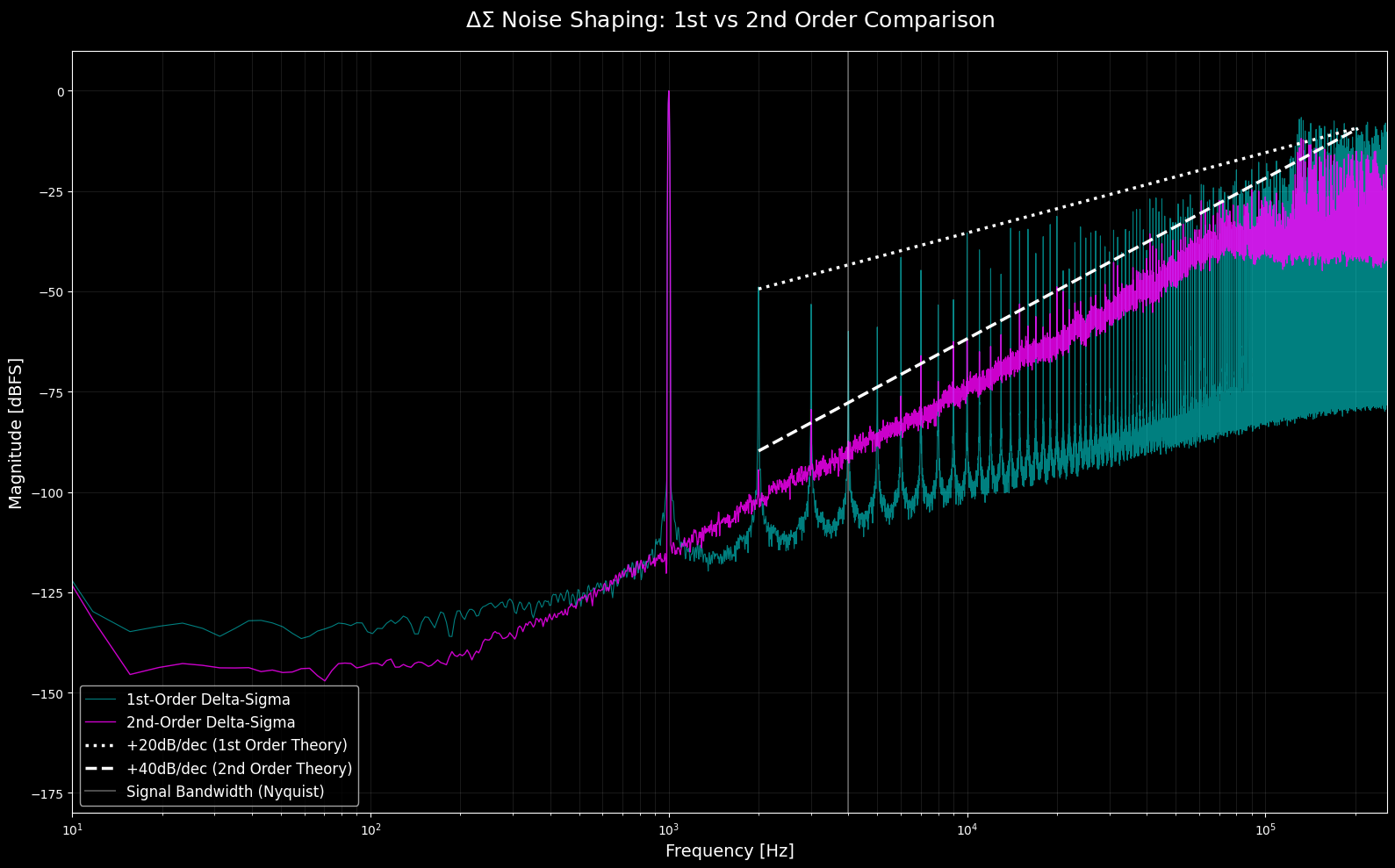
4. ノイズシェーピング：20dB/dec vs 40dB/dec

ΔΣ変調を線形化モデルで考えると、出力 y(z) は「信号成分 ＋ 量子化雑音 × ノイズ伝達関数 (NTF)」として表現されます。

• 1次: NTF(z) = 1 - z^-1 → 低域から高域にかけて 20 dB/dec の傾きで雑音が増加
• 2次: NTF(z) = (1 - z^-1)^2 → 40 dB/dec の傾きで雑音が増加

この理論スロープをPSDプロット上に重ねることで、2次モジュレータがいかに信号帯域の雑音を強力に排除しているかが一目で理解できます。

5. スペクトル解析とSNR評価

解析には Blackman-Harris窓 を用いたWelch法を採用します。これによりサイドローブが抑えられ、広いダイナミックレンジでの評価が可能になります。

• 帯域内SNR計算:

1. 信号近傍（±10% 範囲）の電力を積算
2. 0 ～ BW の範囲から信号電力を除いたものを雑音電力として積算
3. 両者の比をdB単位で算出

6. まとめ

本スクリプトを実行することで、以下の知見が得られます。

• スロープの視覚化: 2次ΔΣのノイズ立ち上がりが、1次よりも急峻（40 dB/dec）であることを確認
• SNRの向上: 理論通り、2次の方が信号帯域内の底辺ノイズが低く、高いSNRを達成することを確認
• アイドルトーンの抑制: ディザの効果により、スペクトル上に不要なピークが立たず、滑らかなノイズシェーピング特性が得られる

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# --- 1. 定数と物理パラメータ ---
fs_high = 512000      # サンプリング周波数 (512 kHz)
decimation_ratio = 64 # オーバーサンプリング比 (OSR)
fs_low = fs_high / decimation_ratio # 出力レート (8 kHz)
f_sig = 1000          # 入力信号周波数 (比較のため1kHzに設定)
N = 2**20             # 高分解能解析用サンプル数
t = np.arange(N) / fs_high

# --- 2. 高精度信号生成 (Analog Domain Simulation) ---
# TPDF Dither: 量子化歪みを完全に白色化し、アイドル・トーンを排除
dither = (np.random.rand(N) + np.random.rand(N) - 1.0) * 1e-5

# アナログ信号の再現 (LPFによる帯域制限)
b_lp, a_lp = signal.butter(2, (fs_low/2) / (fs_high/2))
x_ideal = 0.5 * np.sin(2 * np.pi * f_sig * t)
x_analog = signal.filtfilt(b_lp, a_lp, x_ideal) + dither

# --- 3. こだわりの変調器エンジン (Discrete Time) ---
def ds_modulator(x, order=2, leak=0.99999):
    y = np.zeros(len(x))
    v = np.zeros(order)
    for i in range(len(x)):
        fb = y[i-1] if i > 0 else 0
        if order == 1:
            # 1次: v = v + x - y
            v[0] = v[0] * leak + (x[i] - fb)
        elif order == 2:
            # 2次: v1 = v1 + x - y, v2 = v2 + v1 - y
            v[0] = v[0] * leak + (x[i] - fb)
            v[1] = v[1] * leak + (v[0] - fb)
        y[i] = 1.0 if v[-1] >= 0 else -1.0
    return y

bit1 = ds_modulator(x_analog, order=1)
bit2 = ds_modulator(x_analog, order=2)

# --- 4. 解析: パワースペクトル密度 (PSD) ---
plt.style.use('dark_background')
fig = plt.figure(figsize=(16, 10))

# 高精度窓関数 (Blackman-Harris) によるダイナミックレンジの確保
nperseg = N // 8
f, p1 = signal.welch(bit1, fs_high, window='blackmanharris', nperseg=nperseg)
_, p2 = signal.welch(bit2, fs_high, window='blackmanharris', nperseg=nperseg)

# 信号のピークを0dBFSとして正規化
p_ref = np.max(p1)
p1_db = 10 * np.log10(p1 / p_ref + 1e-25)
p2_db = 10 * np.log10(p2 / p_ref + 1e-25)

# --- 5. 究極の可視化と理論スロープの描画 ---
ax = plt.subplot(1, 1, 1)
ax.semilogx(f, p1_db, color='cyan', alpha=0.5, label='1st-Order Delta-Sigma', lw=0.8)
ax.semilogx(f, p2_db, color='magenta', alpha=0.8, label='2nd-Order Delta-Sigma', lw=1)

# 理論的な傾きガイドの描画 (高精度算出)
# 1次: NTF(z) = 1-z^-1  -> |NTF| ≈ f^1 (20dB/dec)
# 2次: NTF(z) = (1-z^-1)^2 -> |NTF| ≈ f^2 (40dB/dec)
f_guide = np.geomspace(fs_low/4, fs_high/2.5, 100)
# 基点を10kHz付近の実際のデータに合わせて調整
base_f = 10000
idx_f = np.searchsorted(f, base_f)
base_p1 = p1_db[idx_f]
base_p2 = p2_db[idx_f]

guide20 = 20 * np.log10(f_guide / base_f) + base_p1
guide40 = 40 * np.log10(f_guide / base_f) + base_p2

ax.plot(f_guide, guide20, 'w:', lw=2.5, label='+20dB/dec (1st Order Theory)')
ax.plot(f_guide, guide40, 'w--', lw=2.5, label='+40dB/dec (2nd Order Theory)')

# グラフィック設定
ax.set_title("$\Delta\Sigma$ Noise Shaping: 1st vs 2nd Order Comparison", fontsize=18, pad=20)
ax.set_xlabel("Frequency [Hz]", fontsize=14)
ax.set_ylabel("Magnitude [dBFS]", fontsize=14)
ax.set_ylim([-180, 10])
ax.set_xlim([10, fs_high/2])
ax.axvline(fs_low/2, color='white', linestyle='-', alpha=0.3, label='Signal Bandwidth (Nyquist)')
ax.grid(True, which="both", alpha=0.1)
ax.legend(fontsize=12, loc='lower left')

plt.tight_layout()
plt.savefig('ds_order_comparison_high_res.png')

# --- 6. SNRの科学的評価 ---
def calc_snr(f_vals, p_vals, bw, fsig):
    sig_mask = (f_vals > fsig * 0.9) & (f_vals < fsig * 1.1)
    s_pwr = np.sum(p_vals[sig_mask])
    n_mask = (f_vals < bw) & (~sig_mask) & (f_vals > 0)
    n_pwr = np.sum(p_vals[n_mask])
    return 10 * np.log10(s_pwr / n_pwr)

snr1 = calc_snr(f, p1, fs_low/2, f_sig)
snr2 = calc_snr(f, p2, fs_low/2, f_sig)

print(f"--- 解析結果報告 ---")
print(f"1次ΔΣ SNR (in-band): {snr1:.2f} dB")
print(f"2次ΔΣ SNR (in-band): {snr2:.2f} dB")