日本Androidの会秋葉原支部ロボット部 Advent Calendar 2020 9日目です。
映画のアイアンマンやアップグレード(アマゾンプライムビデオ)を見て、ロボットアームが欲しい!と思ったので、作ってみることにしました。
作ったもの
FS90Controller - Github
1リンクアーム - YouTube
2リンクアーム - YouTube
材料
(2リンクアームの場合)
- サーボモータ FS90 2個
- ESP32DevKitCv4 1個
- 単3×4電池ボックス 1個
- 単3電池 4本
- マイクロUSBケーブル 1本
- アームは3Dプリンタで作成
ロボットアームって?
人の腕のような働きをする機械だそうです。
どうやって実現する?
運動学、動力学・・・。とりあえず運動学から勉強することに決めました。
運動学
物体の運動を、変位(位置や速度など)で記述する古典的な力学の一部門。ロボットの運動学には、順運動学と逆運動学があります。
- 順運動学 : 各関節の変位から手先の位置や姿勢を求める
- 逆運動学 : 手先の位置や姿勢から各関節の変位を求める
以降、1リンク~3リンクの運動学の式を淡々と見ていきます。
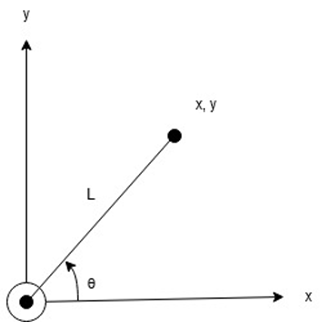
1リンクの運動学
- 順運動学
x = Lcos\theta\\
y = Lsin\theta
- 逆運動学
\theta = tan^{-1}(\frac{y}{x})
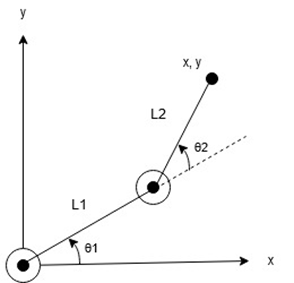
2リンクの運動学
- 順運動学
x = L_1cos\theta_1 + L_2cos(\theta_1 + \theta_2)\\
y = L_1sin\theta_1 + L_2sin(\theta_1 + \theta_2)
- 逆運動学
逆運動学の導出には2つの方法があるようです。
- 順運動学の式から変形
- 余弦定理
以下は順運動学の式からの変形で導出した逆運動学の式です。
\begin{aligned}
\theta_1 &= \pm cos^{-1}(\frac{x^2 + y^2 + L^2_1 + L^2_2}{2L_1\sqrt{x^2 + y^2}}) + tan^{-1}(\frac{y}{x})\\
\theta_2 &= tan^{-1}(\frac{y - L_1sin\theta_1}{x - L_1cos\theta_1}) - \theta_1
\end{aligned}
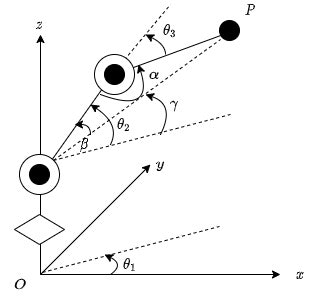
3リンクアームの運動学
順運動学
\begin{aligned}
x &= (L_2cos(\theta_2) + L_3cos(\theta_2 + \theta_3))cos(\theta_1)\\
y &= (L_2cos(\theta_2) + L_3cos(\theta_2 + \theta_3))sin(\theta_1)\\
z &= L_2sin(\theta_2) + L_3sin(\theta_2 + \theta_3) + L_1
\end{aligned}
逆運動学
余弦定理を使って求めました。
\begin{aligned}
\overline{OP} &= \sqrt{x^2 + y^2}\\
\alpha &= cos^{-1}(\frac{L_2^2 + L_3^2 - \overline{OP}^2}{2L_2L_3})\\
\beta &= cos^{-1}(\frac{L_2^2 + \overline{OP}^2 - L_3^2}{2L_2\overline{OP}})\\
\gamma &= sin^{-1}(\frac{z - L_1}{\overline{OP}})\\
\theta_1 &= tan^{-1}(\frac{y}{x})\\
\theta_2 &= \gamma \mp\beta\\
\theta_3 &= \pm(\pi - \alpha)
\end{aligned}
アームとアプリケーション作成
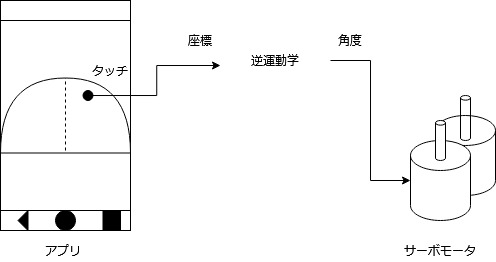
サーボモータは秋月電子で購入したFS90を使いました。アーム部分は3Dプリンタでデザインしたものを使っています。ついでにスマホで操作するためにAndroidアプリを作りました。動作は下の図のようになります。