DeepLearningは、既にいろんな機械学習の基盤として実用されていますが、個人でそれを利用するだけでなく、少しでも理解したいと思っていました。
そんな時、Chainerで線画着色を実装した方の記事をみました。 (http://qiita.com/taizan/items/cf77fd37ec3a0bef5d9d)
画像系は学習過程を見てわかりやすいし、そもそもDeepLearningの最初は画像処理だった、ということで、これを出来るだけソースのコピーをせずにTensorflowで実装してみました。
なお、実際には始める前にデータセットの収集から始めました。大体20万枚くらいは集めましたが、この収集については特に書くことがない(頑張るだけ)ので省略します。実際には収集と変換だけで2週間以上かかってます。
学習用画像について
学習用のデータは、次のような画像になるように加工しています。
- 高さ・幅はそれぞれ128px
- 線画はオリジナルを変換したものをリサイズ
- リサイズ時の補完形式はINTER_AREA
- ちなみに、これがINTER_CUBICだと、シャギーが発生してしまい、色々とオリジナルと異なる感じになってしまいます
わりと効くのはINTER_AREAで画像縮小することで、これをしないと余計なシャギーが発生したり、線画がガタガタになったりで、ちゃんと(?)学習が進まないケースが多くありました。
着色の学習(最初のアプローチ)
着色の学習を行うとして大事なのは、 何が特徴変数となるか を考えてみました。着色をする、ということは、少なくとも線画の特徴を残しつつ、空白の部分に色を付ける必要があります。
若干流れは違いますが、こういう生成系のネットワークで、AutoEncoderというものがあることを知りました。元々は機械学習のデータ生成とかで利用されているもののようで、すでにMNISTの画像を利用したAutoEncoderみたいなのは色々見られます。
http://qiita.com/kenmatsu4/items/99d4a54d5a57405ecaf8
AutoEncoderをCNNで実装する場合、大体は以下のような流れになります。
- Convolution+max poolingを利用して特徴を抽出して、高解像度から多数の特徴を抽出する
- 抽出した特徴量から、deconvolutionで画像を復元する
- deconvolutionという場合とfractional convolutionという場合があり、アップスケールする場合のconvolutionは、fractional convolutionというのが正しいようです
- deconvolutionした画像と教師画像を、loglossと呼ばれる損失関数の値を最小化するように最適化する
loglossとはこれです。バイナリエントロピーとも呼ばれています。
DeepLearningとか機械学習とかの数式ではlogが非常によく出てくるので、指数対数の法則を思い出しながら数式を見てました。。。
Kerasでは、Kerasの利用例としてautoencoderの実装というのが公式で公開されています。kerasでは損失関数の一つとして、loglossが用意されているので、全体として非常にわかりやすい記述になっています。
損失関数としては、これの他にオリジナルとの二乗誤差を最小化する、という方法も利用されているようです。
しかし、愚直にAutoEncoderの入力を線画、出力を元絵としても、そもそも線が消えてしまって何がなんやら、という形になってしまいました。(線画から線画ならそれなりになってきます。そりゃそうだ)
U-Net
そこで、大元のQiitaの記事でも利用していると記載されている、U-Netを調べてみました。
U-Netは、元々癌細胞の検出において、Image Segmentationを行うために利用されたものです。Convolution+DownsamplingとUpsampling+Convolutionを組み合わせて、全体としてU字を描いたようなアーキテクチャになっていることから、このような名前になったようです。
特徴として、Downsamplingした特徴量を、同じ層のUpsamplingした層に加算する、ということを行っています。これは、ある程度特徴量の次元を減らして行くと、そこから復元する際に、元の特徴量が速やかに失われていってしまうため、元々の画像の特徴を残し、かつ強調するためのようです。特に高解像度の画像を利用していると、これが顕著です。
(512x512の画像を、64x64くらいまで落とす程度であれば、ギリギリ元の特徴量が残った状態にできる。32x32だとほとんど失われる)
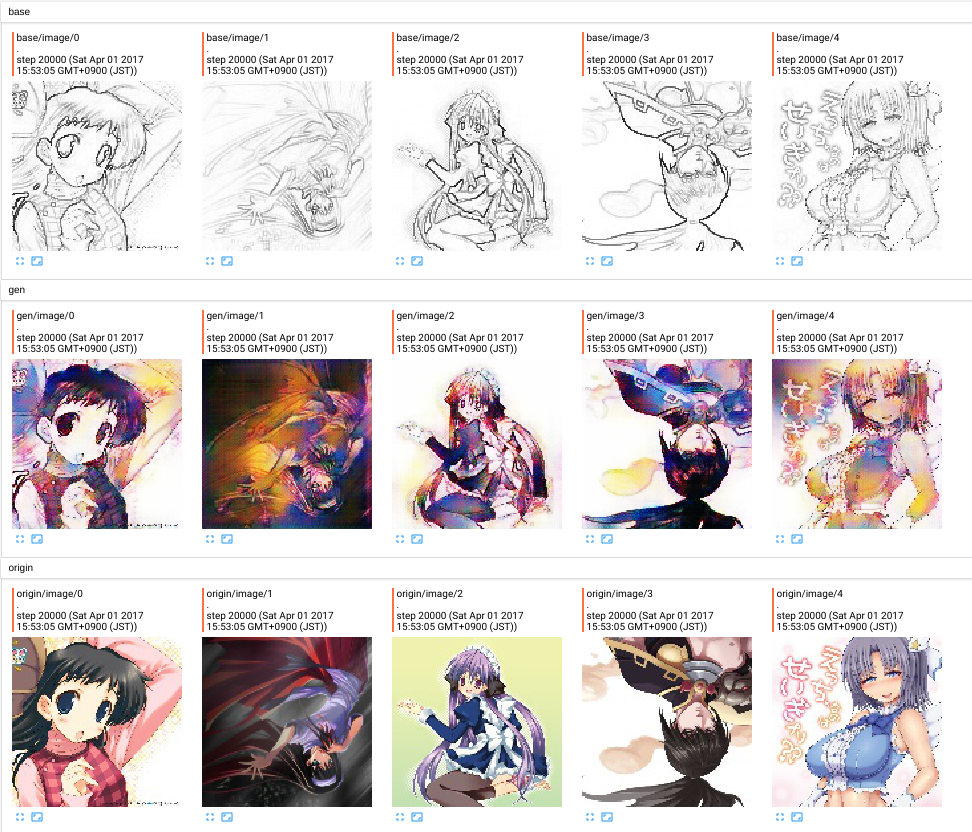
U-Netの導入前後で、AutoEncoderにおけるGenerator部分の精度が全く違います。最初は線部分にも色んな色がついてきますが、学習が進むにつれ、U-Netの効果で線部分(=分離)はかなりいい感じになってきます。
ただし、線画以外の部分については、影とかは徐々にそれっぽくなってはきますが、色が一様になってしまう問題に当たりました。
学習している間の画像を見ていくと、最初は何らかの色(RGBのどれか一色)が強いんですが、その色がどんどん元の線画と同じような色になっていって、そこで収束してしまう感じです。具体的に言うと、全体がセピア色的な感じになったり、要は全体として均一であれば誤差の平均としては0になるよね、という感じです。
(そりゃそうだって感じですが・・・)
このときは誤差関数として二乗誤差の平均を利用していました
さて困った、ということでAutoEncoderというか、生成系で色々調べていくと、DCGANに行き着きました。
DCGAN
DCGANは、この論文が元とされる、敵対的ネットワークを利用した教師なし学習を、DeepLearningに適用したネットワークです。
https://arxiv.org/pdf/1511.06434.pdf
GANの原論文は https://papers.nips.cc/paper/5423-generative-adversarial-nets.pdf 。
なお、論文の中で出てくる KL-divergenceとJS-divergenceというのがさっぱりわかりませんでした。
こちら http://blog.vingow.com/tech/numpy-jensen-shannon/ を参考にしてなんとなく理解できましたが、
改めて(この分野では)数学って大事なんや・・・って思い知らされました
DCGANについて、非常に参考になるページがこれです(ぶっちゃけ実装がかなりそのまま載ってるので、参考にし過ぎないようにするのが大変です)
https://bamos.github.io/2016/08/09/deep-completion/
https://elix-tech.github.io/ja/2017/02/06/gan.html
DCGANでは、GANを導入する上で重要なポイントを挙げています。
- Batch normalizationをGenerator/Discriminator両方に入れる
- Batch normalizationについては https://deepage.net/deep_learning/2016/10/26/batch_normalization.html を参考にしてください。やってることはいまいちわかってません(ぉ
- Max Poolingを利用せず、Strided convolutionを利用する
- 画像サイズを減らす際に、kernel sizeとstrideを大きくしたConvolutionを利用します
- 基本的にReluだけを利用する
- DiscriminatorはLeakyRelu、Generatorの最終層はTanhを利用する、と原論文では書いてます
- Discriminatorではfully-connected(Denseとも呼ばれるらしい)をしない
- 私はflattenして行列かけて、というシンプルな形(これがfully-connectedらしいですが)にしました
なお、DCGANの論文で一番(?)有効なのは、Batch normalizationとADAM Optimizerの導入だった、と記述している方もいました。
ちなみに、これ以外にも
- ADAMのLearning rateはかなり低くする
- ADAMのbeta1は0.5程度から始めてみる
というのが重要とされていました。
ただ、実際に実装してみると、そもそも収束も何も、Discriminatorが強くなりすぎる問題が出てきました。GANの学習はかなり不安定ということは、色んな所で言われているのを見ましたが、それをまざまざと見せつけられた感じです。
DCGANのチューニング大会
GANそのものの学習が安定しないことについては、以下でも言及されています。
https://www.slideshare.net/DaisukeOkanohara/dnn-62218756
さらに色々見ていくと、 https://www.slideshare.net/pfi/iibmp2016-okanohara-deep-generative-models-for-representation-learning の中で紹介されていたページで、Generatorにおける学習が進まない問題に対して新しい低減をしているのを見つけました。
アドレスの.vcを見てベンチャーキャピタル?ってなったのは私だけじゃないはず。それは置いておいて、 この中では、GANの原論文でGeneratorにおける D(G(z)) を最小化する式について、理論上の 1 - D(G(z)) では、学習の初期でGeneratorが未熟な際に却下されやすくなり、結果として学習が進まないため、 D(G(z)) を最小化している、という一文を取り上げています。
実際、Discriminatorの学習の方がパラメータが明らかに少ない分進みやすく、Generatorは進みづらいため、最初の方では、DiscriminatorはGeneratorに対して容易く却下する=正解の分布から出てきた確率が低い、となり、back propagationが非常に小さくなってしまいます。
import math
probability = 0.01
math.log(0.99) # => -0.010050...
math.log(0.9) # => -0.10050...
記事の著者は、この非線形変換によって、収束を早くする効果はあるが、経験的に安定して収束しないと書いています。また、この変換を行うことで、理論上JSダイバージェンスを基礎としていた部分との理論的な繋がりが切れ、一体何を最小化しているのかがわからなくなっているとも書いています。元々良くわかっていない人からするとそうなんや・・・としかなりませんが、確かに実用重視な感じはします。
そこで、Generatorの学習を行うための式として、新しい形式を提案しています。新しい形式は、元々のJSダイバージェンスの代わりに、 KLダイバージェンス KL[Q||P] を利用しています。これは、D(G(x) と 1 - D(G(x)) 間の差異の大きさを表し、この距離を最小化する、という式に帰着させています(きっと)。記事中では、Generatorの更新式として、次のようなものはどうか?としています。
\theta_{t+1} \leftarrow \theta_{t} + \varepsilon_{t} \frac{\partial}{\partial \theta} \mathbb{e}_{z \backsim Z} \log \frac{D(G(z;\theta_{t});\psi_{t+1})}{1 - D(G(z;\theta_{t});\psi_{t+1})}
記号だけ見てると暗号です。偏微分も習っていない人からすると何がなんやらもうわかりませんが、ここでは右式のlog〜を最小化すればいい、ということのようです。
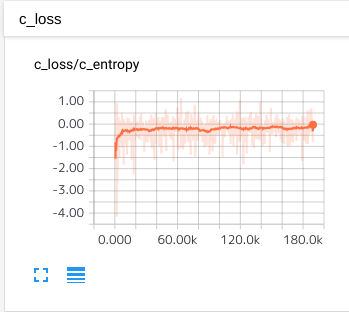
原論文では、GANにおける本物の分布におけるDiscriminatorの結果と、生成物の分布におけるDiscriminatorの結果を加算したものの最小値(不正確ですが感覚的に)は、 log(4)=約1.39 であることが証明されています。なので、Discriminatorがいい感じかどうかの判定基準の一つとして、この損失関数の値がこの値に収束していっているか、を見るという手段があります。
Generator側の判断基準については、DCGANでは今の所無いらしいので、基本的に目視で見ないとなりません。
着色の様子を見てみる
Tensorflow最大(個人的に)の特徴である、Tensorboardを利用すると、学習途中の画像がどんな感じか、というのを手軽に見ることが出来ます。
進めてみるとこんな感じになっていきました。油断するとDiscriminatorが強くなりすぎてあっという間によくわかんないものになってしまうのが玉に瑕です。
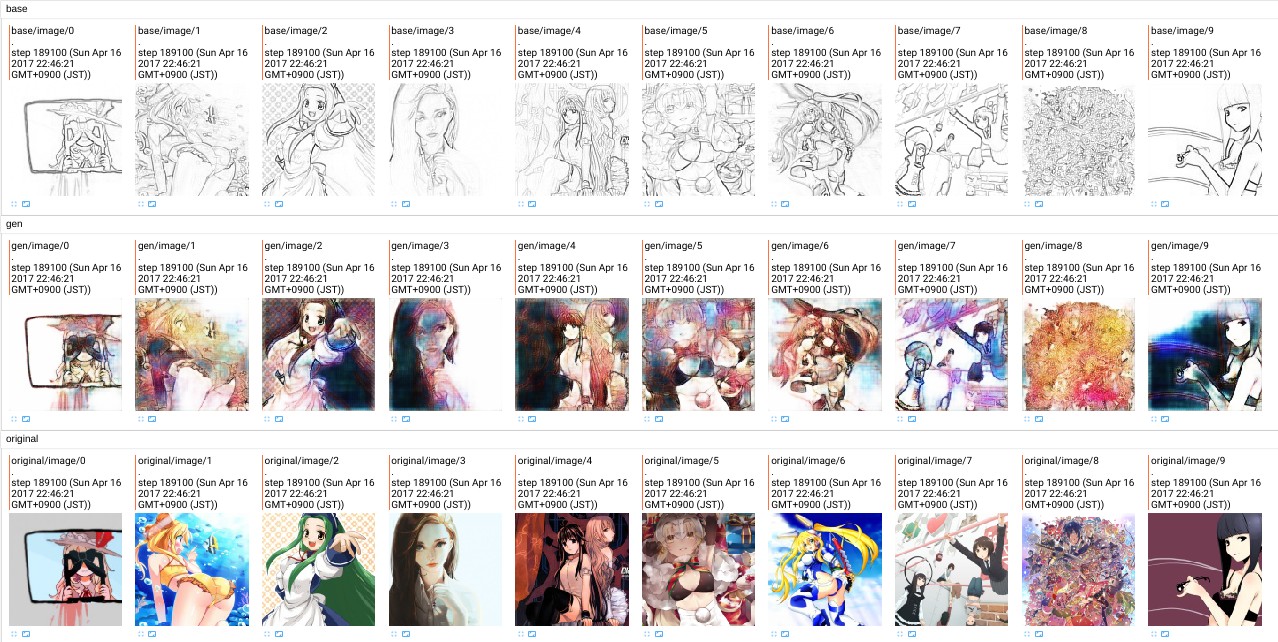
また、損失関数としてL1 distanceを加えたりしています。加える前後ではこれくらいの差が出来ます。
L1 Loss追加。40000step経過(1step=画像10枚)
何となく見るとわかりますが、この程度のiterationではまだまだ甘いと言わざるを得ません(データセットは画像15万枚程)。また、結構色の付き方も癖があり、特定の色にかたよる傾向が結構強いです。モードの崩壊というほどのものなのかはまだなんとも言えませんが・・・。
Wasserstein GANを試す
つい数カ月前、新しいGAN系のアルゴリズムが出ました。wassersteinはドイツ語のようで、ワッサーステインと読むようです。
GANの問題点であった
- 学習が不安定
- モードの崩壊が起こる
というのを、新しいアルゴリズムを持って改善できる、という内容です。一通り読んで見た感じだと、JS divergenceやKL divergenceは有用な勾配が無くなるケースがあるから不安定だけど、提案しているEM distanceだとちゃんと勾配があるから、基本的に不安定になることもないし、そもそも崩壊することもないよ、という主張(と理解しました)のようです。書いてある内容自体、かなり高度な数学の話であるため、詳細まで読んでも全く理解ができませんし、Appendixにあった証明は言わずもがなです。
しかし、アルゴリズムをみた感じは結構シンプルな実装になりそうでした。
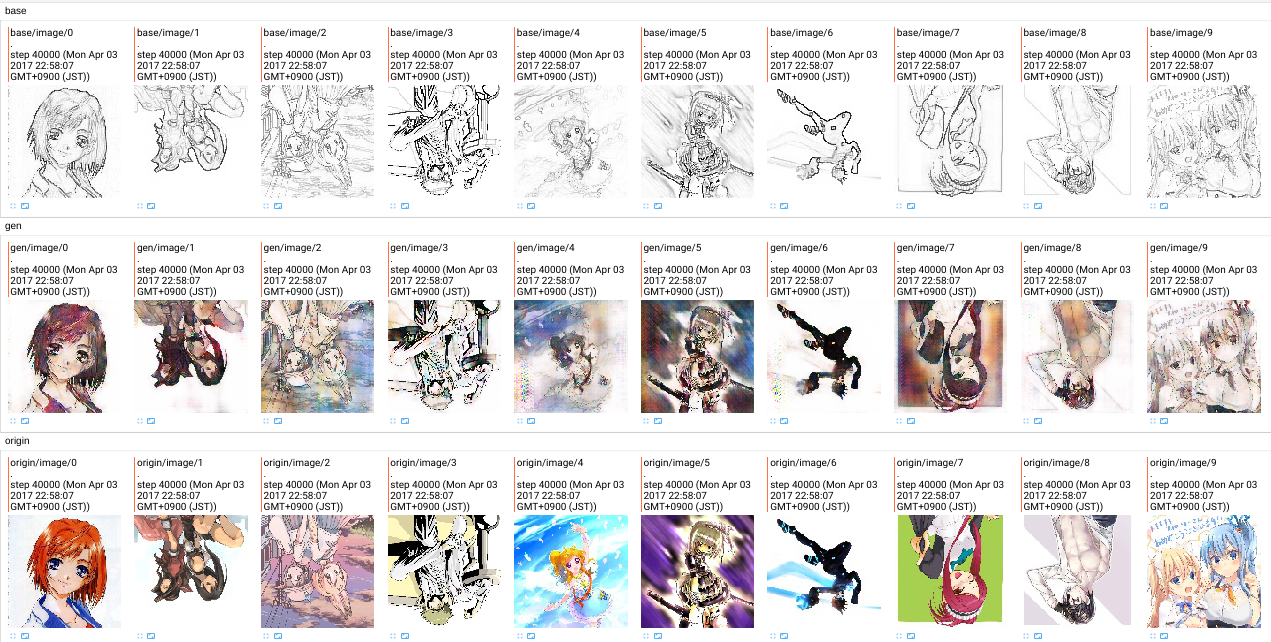
内部で言っている critic と、GANでいうDiscriminatorが同じものを指している、となんとなく理解できると、DCGAN的な実装からそこまで変更しなくてもいけそう、という感じだったので、今のネットワークに適用してみました。
WGANは学習が安定する代償として、学習がかなり遅い、という副作用があります。上の画像は19万ほど回していますが、これでも恐らく原論文の1/10程度です。(stepの数え方がちょっと違うので)
また、L1 lossの追加も行っているため、その辺りのハイパーパラメータの調整が結構難儀します。
これから
まだWGANの学習が収束していないので、ある程度収束するまではしばらく回して見ようと思います。19万回すのに8時間とかかかりましたんで、収束するまでは一週間とかかかるんじゃなかろうか・・・。
収集した画像には、収集元から取得したタグとかも含まれているので、これを利用したりもしてみたいです。そういったことをしている論文も見つけているので、色々と試していこうと思います。