学習率最適化手法
学習率とは、勾配降下法において、「勾配に沿って一度にどれだけ降りていくか」を決めるもの。
学習率の値が大きい場合
→最適値にいつまでもたどり着かず発散してしまう
学習率の値が小さい場合
→発散することはないが、小さすぎると収束するまでに時間がかかってしまう
大域局所最適値に収束しづらくなる
その解決のために考えだされたのが学習率最適化手法である。
代表的なもの4つ
・モーメンタム
・AdaGrad
・RMSProp
・Adam
Adam ※現在最も使われている!!
モメンタム×RMSprop両方を使っている
・モメンタムの、過去の勾配の指数関数的減衰平均
・RMSpropの、過去の勾配の2乗の指数関数的減衰平均
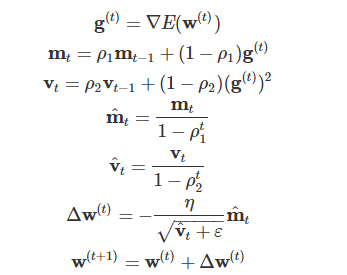
【実装例】Adam
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
# batch_normalizationの設定 ================================
# use_batchnorm = True
use_batchnorm = False
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
use_batchnorm=use_batchnorm)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
beta1 = 0.9
beta2 = 0.999
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
if i == 0:
m = {}
v = {}
learning_rate_t = learning_rate * np.sqrt(1.0 - beta2 ** (i + 1)) / (1.0 - beta1 ** (i + 1))
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
if i == 0:
m[key] = np.zeros_like(network.params[key])
v[key] = np.zeros_like(network.params[key])
m[key] += (1 - beta1) * (grad[key] - m[key])
v[key] += (1 - beta2) * (grad[key] ** 2 - v[key])
network.params[key] -= learning_rate_t * m[key] / (np.sqrt(v[key]) + 1e-7)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
【確認テスト】

①モメンタム (前回の重みを利用!!)

Vt=「前回の重みと慣性の積」-「誤差をパラメーターで微分したものと学習率の積」
《メリット》
・局所最適解にはならず、大域的最適解となる
・谷間についてから最も低い位置(最適地値)にいくまでの時間が早い
②AdaGrad (
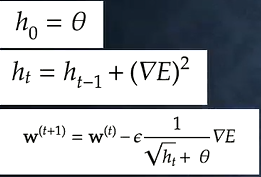
誤差をパラメーターで微分したものと再定義した学習率の積を減算する
《メリット》(これまでの学習率を活用)
・勾配の緩やかな斜面に対して、最適値に近づける
⇒課題:学習率が徐々に小さくなるので、鞍点問題を引き起こすことが多い
③RMSprop
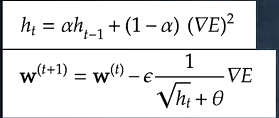
Adagradの進化形。誤差をパラメーターで微分したものと再定義した学習率の積を減算する
前回の学習率をどれだけ利用するかをパラメーターαで調整できる
《メリット》
・局所的最適解にはならず、大域的最適解となる。
・ハイパーパラメーターの調整が必要な場合が少ない