ターニングポイントを探せ！ 【change finderで時系列の変化点抽出】

#背景
私結構、歴史の本が好きでたまに読んでます。最近は失敗の本質を読みました。この本、太平洋戦争のターニングポイントでどういう事が起こっていたかを組織論の観点で語っていて、とても面白かったです。
この本を読みながら、「ターニングポイントって後から振り返って定量的に把握できるものだろうか？」という疑問を持ちました。
そしたらありました。時系列の変化点を抽出するアルゴリズムが。

#異常検知・変化検知の問題の種類
そもそも、異常検知・変化検知ってどういう問題があるんでしょうか。
異常検知入門
の12ページを参考に、3分類してみました。

タスク	概要
外れ値検出問題	静的。あるデータ点が分布から大きく外れているか
変化点検出問題	動的。対象に変化が起きたか否か、その時点はどこか
異常状態検出	動的。今の対象の状態が異常か正常か。

さらに具体的に書き始めると超長文になってしまうので今回はスキップします。
異常検知・変化検知の概要を知りたい方は異常検知と変化検知のまとめ　数式なしの記事がオススメです。

今回はこの中の「変化点検出」について時系列データの変化点検出に使用されるアルゴリズムの紹介とpythonにモジュールがあるので実際に試してみました、という内容です。

#時系列の変化点抽出のアルゴリズム
※ここからのアルゴリズムの話は、以下の資料を参考にまとめ直したものになります。
SDARアルゴリズムと統計的手法による時系列からの外れ値と変化点の検出
異常値検知のための基本的モデルの考察

##従来提唱されてきた変化点検知アルゴリズム
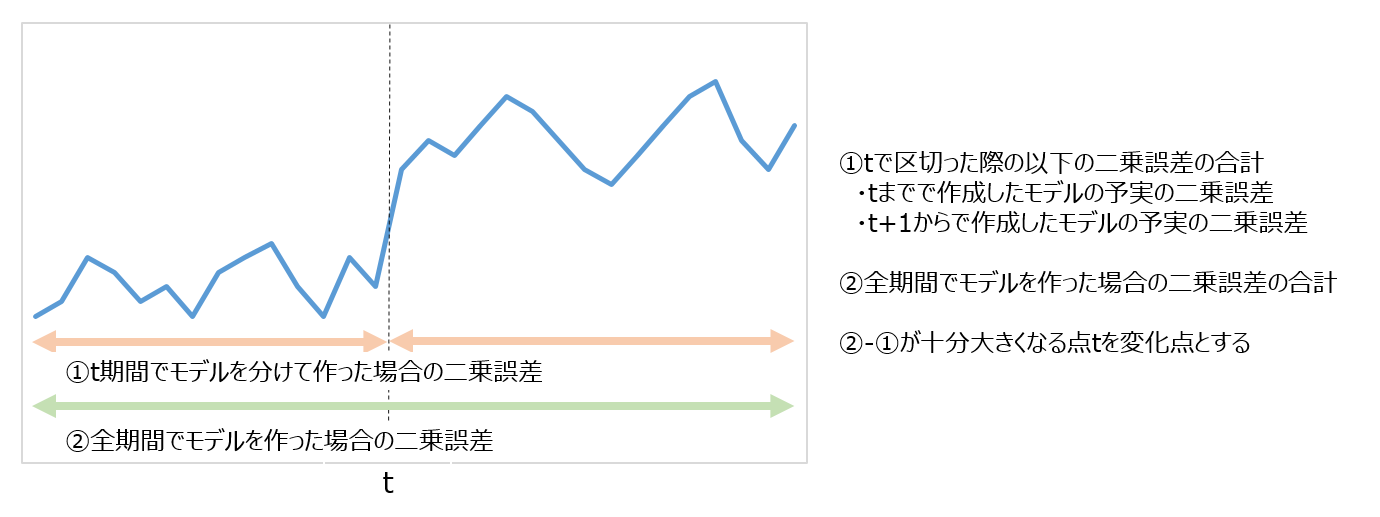
従来提唱されてきた考え方は非常にシンプルです。
①時系列データの全体を使って構築した時系列モデル（ARモデルなど）
②ある時点tで区切って分けて構築した時系列モデル
の両方を用意し、

①お互いのモデルで未来の予測値を算出
②お互いのモデルで予測値と実測値を比較して、実績値との二乗誤差の計算
を行い、

「時系列データの全体を使って構築した時系列モデルの二乗誤差」から
「ある時点tで区切って分けて構築した時系列モデルの二乗誤差」を引いて
それが十分大きくなる場合に
「tで変化が発生している」と定義する、というものです。

##（参考）時系列のARモデル
一応参考のために、ARモデルの数式だけ記載しておきます。
詳しい解説などは他文献・WEBサイトなどでご確認ください。
d次元のARモデルは次のように記述できます。

z_t = \sum_{i=1}^{k}A_iz_{t-i}+\varepsilon

$A_i$は係数行列、$\varepsilon$は平均0、分散共分散行列が$\Sigma$であるノイズになります。

##従来のアルゴリズムの問題点
上記のアルゴリズムには、以下のような問題がありました。

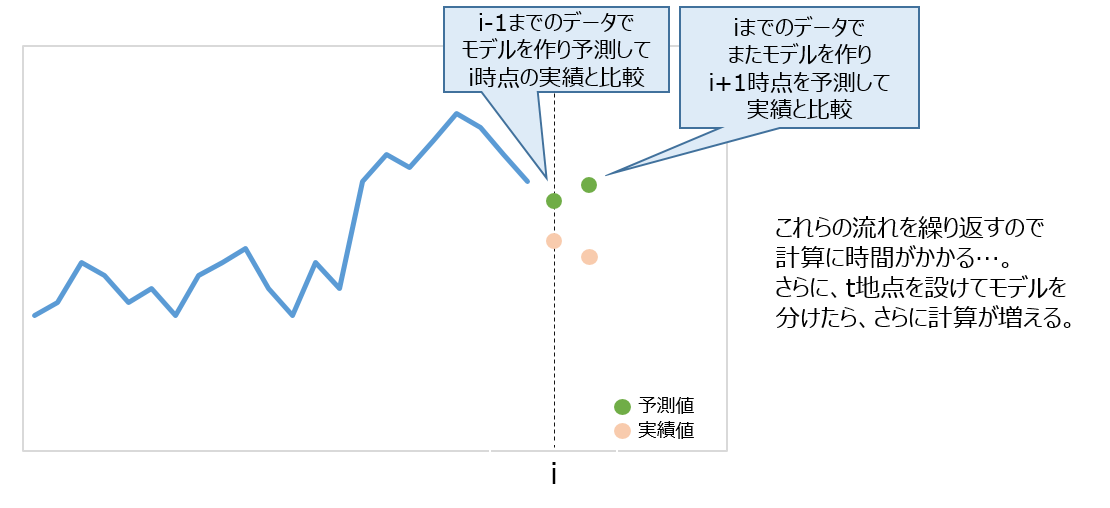
###①計算時間が膨大

• 未来のt+1時点を予測する度にt地点までのデータを使って新しくパラメータを計算し直す必要がある
• しかもt地点を探索的に探す必要もあり、計算量が膨大になる

###②非定常なデータに対応できない

• ここで規定している時系列モデルは定常性を持ったデータに適用することが前提のため、非定常なデータには対応できない
• 変化が発生しているデータを扱う関係上、上記の仮定を置くのが難しい

#変化点検出の手法の１つ Change Finder
上記のような問題点を解決するために、ARモデルの構築についてパラメータなどの計算をオンライン処理で行ったSDAR（Sequentially Discounting Auto Regressive）アルゴリズムを使った「Change Finder」という手法が生み出されました。

① 時系列データ毎に変化スコアを算出し、高いスコアの部分を「変化」とみなす
② パラメータ計算は最尤推定（をちょっと応用した）方法で簡易的に求めている
③ データが更新された場合のパラメータは、過去のパラメータと更新されたデータから求めている
　- ②と③によって、従来の方法から計算量が減る
④ モデルのパラメータを求める際、過去のデータの影響を小さくするような「忘却パラメータ」を設定する
　- 上記を適切に設定することによって、過去の時系列データの性質が違ってもその影響を小さくすることができ、非定常なデータにもある程度対応が可能になる
④ 外れ値・変化点を区別して抽出
　- 上記を区別するため、学習を二段階で実施している（後述）

要するに「従来よりも早くて正確！」ということです。

#SDARモデル
SDARモデルでは、時系列データからARモデルに基づく確率密度関数を求め、その対数尤度関数を近似して求めます（今回の記事では対数尤度関数省略。知りたい方はこちらをご確認ください。）モデルのパラメータは、求めた対数尤度関数に忘却係数を掛け合わせた値が最大化する時の値を推定します。

具体的には以下になります。
確率過程$p$に対して $ x^{t-1} = x_1,x_2,…,x_{t-1}$を与える$x_t$の条件付き密度関数を考えるために、$ p(x_t | x^{t-1}) $のような表記法を用いたとき、SDARモデルのパラメータ$A$,$\mu$,$\Sigma$は$I$が最大となる時の値を用います。

I = \sum_{i=1}^{t}(1-r)^{t-i}\log P(x_i|x^{i-1},A_1,…,A_k,\mu,\Sigma)

ここで$r$は忘却パラメータ、$A$はARモデルのパラメータ、$k$はARモデルの次数、$\Sigma$は分散共分散行列です。

また、今回の記事では対数尤度関数の導出やユールウォーカー方程式を使ったパラメータの導出については省略します。知りたい方はこちらの論文の該当箇所をご確認ください。

#Change Finderでの変化点算出方法まとめ
###第一段階学習
①SDARモデルで、各時点における時系列モデル（＝各時点までのデータを元にした確率密度関数）を構築
②①で構築したモデルを元に、次の時点の実測値が出てくる尤度を求める
③この確率の対数損失を求め、外れ値スコアとする

外れ値スコアは以下のように計算します。

Score(x_t) = -\log P_{t-1}(x_t|x^{t-1})

###外れ値スコアの平滑化
幅$W > 0$を設定して、その幅の中で外れ値スコアを平滑化する。
平滑化を行うことで、外れ値の状態ではなく、その状態が長く続いているかどうか（＝変化しているかどうか）を判別することができます。

一応数式でも表すと、t時点における平滑化されたスコアを$y_t$とおくと以下のように計算できます。

y_t = \frac{1}{W}\sum_{t=t-W+1}^{t}Score(x_i)

###第二段階学習
①平滑化で得られたスコアをさらにSDARモデルで学習
②①で構築したモデルを元に、次の時点の実測値が出てくる「確率」（忘却係数による調整あり）を求める
③この確率の対数損失を求め、変化点スコアとする

#サンプルコード
こちらのサンプルコードをそのまま引用させて頂きました。3種類の正規分布に従う乱数を発生させて、その変化点を見ています。

# -*- coding: utf-
import matplotlib.pyplot as plt
import changefinder
import numpy as np
data=np.concatenate([np.random.normal(0.7, 0.05, 300), 
np.random.normal(1.5, 0.05, 300),
np.random.normal(0.6, 0.05, 300),
np.random.normal(1.3, 0.05, 300)])

cf = changefinder.ChangeFinder(r=0.01, order=1, smooth=7)

ret = []
for i in data:
    score = cf.update(i)
    ret.append(score)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(ret)
ax2 = ax.twinx()
ax2.plot(data,'r')
plt.show()

結果は、以下のようになりました。
赤線が元のデータで、青線が変化点スコアになります。

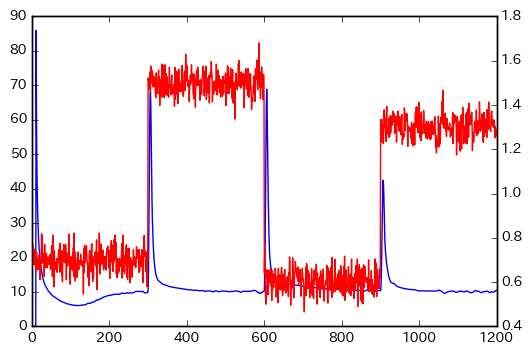
#changefinderで設定しているパラメータ
上のサンプルコードだとchangefinder.ChangeFinder(r=0.01, order=1, smooth=7)というパラメータを設定しました。
それぞれのパラメータの簡易的な説明をします。

$r$：忘却パラメータ
で、確率密度関数を算出する際どの程度過去の影響をコントロールするかを示しています。SDARモデルの数式を見てわかるように、この値を小さくすると過去の影響が大きくなり、変化点のバラツキが大きくなります。

order：ARモデルの次数
どこまで過去の値をモデルに組み込むかを設定します。このパラメータの決め方をどう捉えるかは私の中でまだ答えがありません。（シンプルに次数をAICやBICベースで決めても非定常なデータだとあまり意味が無いし、定常性を持つように加工してから次数を推定したところでこのモデルを当てはめる時系列データ自体は非定常だし…）

smooth：平滑化の範囲
ここを長くすれば長くするほど外れ値ではなく「変化」が捉えられますが、大きくしすぎるとそもそも変化そのものが捉えづらくなります。

#某企業の株価の変化点抽出
上記はサンプルデータを作成して変化点を抽出しましたが、
企業の株価から、その企業のターニングポイントを可視化することはできるのかちょっとやってみました。
以下、データ分析や分析システム提供を主事業にする「某企業」の株価の変化点を確認してみました。

最初に、必要なライブラリをインポートします。

# -*- coding: utf-

## 今回使用したライブラリやおまじない
# changefinder周りで必要なもの

import changefinder
#必要に応じて:pip install changefinder
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from statsmodels.tsa import ar_model

# スクレイピング周りで必要なもの

import urllib2
import requests
import lxml
from bs4 import BeautifulSoup
import time

次に、株価データを取得します。
今回はこのサイトからデータを取得しました。

## データ取得

dates = []
stock = []

for i in xrange(1,7):
    #今回は某企業の2011-2016の株価を取得します
    url = urllib2.urlopen('http://k-db.com/stocks/3655-T/1d/201' + str(i))
    #一応スリープ入れる
    time.sleep(5)
    soup = BeautifulSoup(url)
    #日付の数を取得
    n_dates = len(soup.find_all("td",{"class": "b"}))
    for j in range(n_dates):
        date = str(soup.find_all("td",{"class": "l"})[j].text)
        stock_day = float(soup.find_all("td",{"class": "b"})[j].text)
        dates.append(date)
        stock.append(stock_day)

stock_pd = pd.Series(stock,index=dates).sort_index()
print stock_pd.head(10)

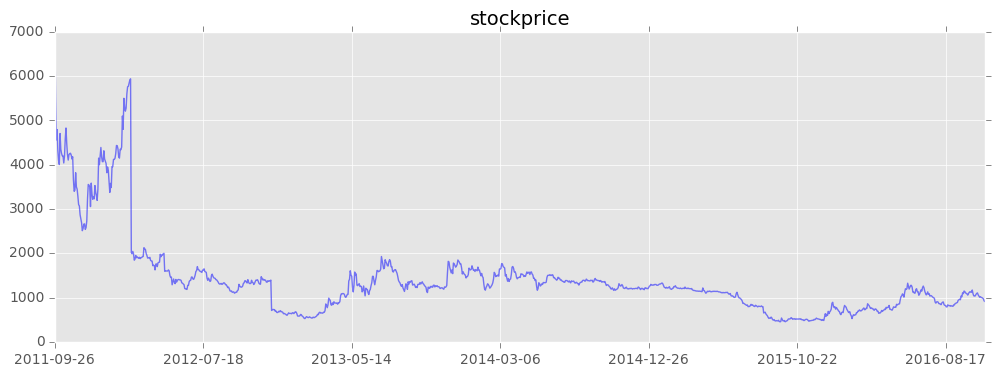
取得したデータを可視化してみます。

## 可視化

plt.style.use('ggplot')
stock_pd.plot(figsize = (12,4),alpha = 0.5,color = 'b')
plt.title('stockprice', size=14)

この某企業は、2011年～2012年で株価が高く、そこから下がって
そこからは（若干下がりつつも）安定した動きをしているように見えます。

さて、ではいよいよchangefinderで変化スコアの算出です。

## change finder

cf = changefinder.ChangeFinder(r = 0.01, order = 3, smooth = 14)

change = []
for i in stock_pd:
    score = cf.update(i)
    change.append(score)

change_pd = pd.Series(change,index=dates)

stock_price = stock_pd.plot(figsize = (12,4), alpha = 0.5, color = 'b',x_compat=True)
ax2 = stock_price.twinx()
ax2.plot(change_pd, alpha=0.5, color = 'r')
plt.title('stockprice(blue) & changescore(red)', size=14)

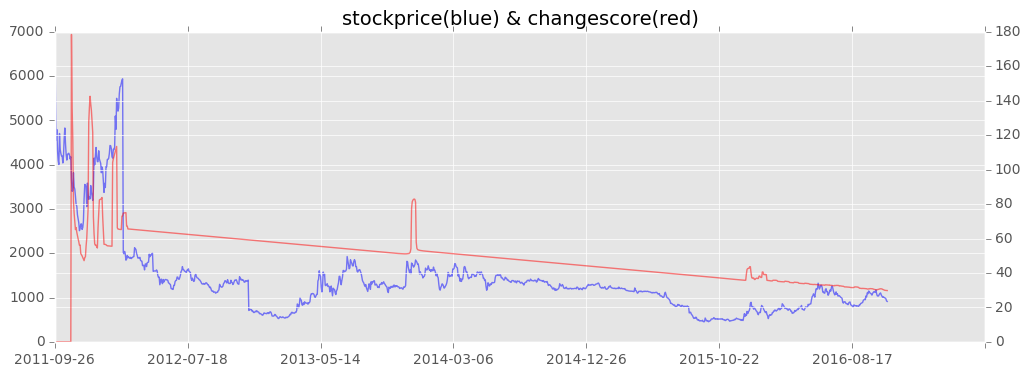
結果は以下のようになりました。

2011年～2012年にかけて変化の連続ですね。その後は2014年1月頃にも変化があるように見えます。
実はこの企業、2011年9月に東証1部に上場しているのです。なので最初は株価が安定していなかったことがわかりますね。あと、2014年1月あたりだと、某企業との合弁会社設立を行ったりしているので、経営的にかなり攻めていた？時期と言えるかもしれません。
後は変化点が低いですね。基本的にあまり強烈な変化でガタガタすることなく、安定している企業…ということができるかも？？

#まだわからないこと
①このアルゴリズムですが、実際動かすと「パラメータを変えるとすぐに変化点が変わってしまう」ことがわかります。とはいえ、各パラメータの適切な決め方がわからなかったので、今回は「探索的に」結果を確認しながらパラメータを決めていきました。ここらへんのうまい調整の仕方、わかる方いればご教授頂けると幸いです…。
②本当に非定常データにも「対応できている」と言えるのだろうか？確かに忘却パラメータ次第で過去の影響は小さくなっているが、何をもってして「非定常でも大丈夫」と言い切れるのかはまだ納得がいっていない。

#その他
また、今回はARモデルをベースに変化点抽出をしましたが、changefinderには
ARIMAモデルベースで変化スコアを算出するメソッドも存在します。
ここはまだ理論まで見ていないので、今後気が向いたら記載します。

#まとめ

• 時系列の変化点抽出に、オンライン処理＋忘却効果を考えたSDARモデルを使ったchangefinderというアルゴリズムがある
• 伝統的な変化点抽出のロジックよりは計算が簡単＋非定常にも対応可能（らしい）
• パラメータチューニングなどは今後改善の余地あり（むしろ教えてください）