異常検知と変化検知のまとめ 数式なし

この記事は、「Machine Learning Advent Calendar 2015」の17日目の記事になります。

「異常検知と変化検知」の本は良書だったので買うのに迷っている人のためにまとめてみました。
間違いがあれば、ご指摘頂けると幸いです。

数式を見て厳密に理解したい方は書籍購入をおススメします。
またコードに直すときはアルゴリズムが必要です。
本書籍ではアルゴリズムも記述してくれいてるのでおススメできます。
本記事ではアルゴリズムには言及しません。

#この記事で得られるもの

１：異常検知における手法の種類
２：異常検知における手法をどのシーンで使用するか
３：異常検知における機械学習をどのように応用するか

以上です。

#本記事の見方

利用シーンと簡単な手法を記述したので、利用シーン

##異常検知の基本的な所だけ抑えたい

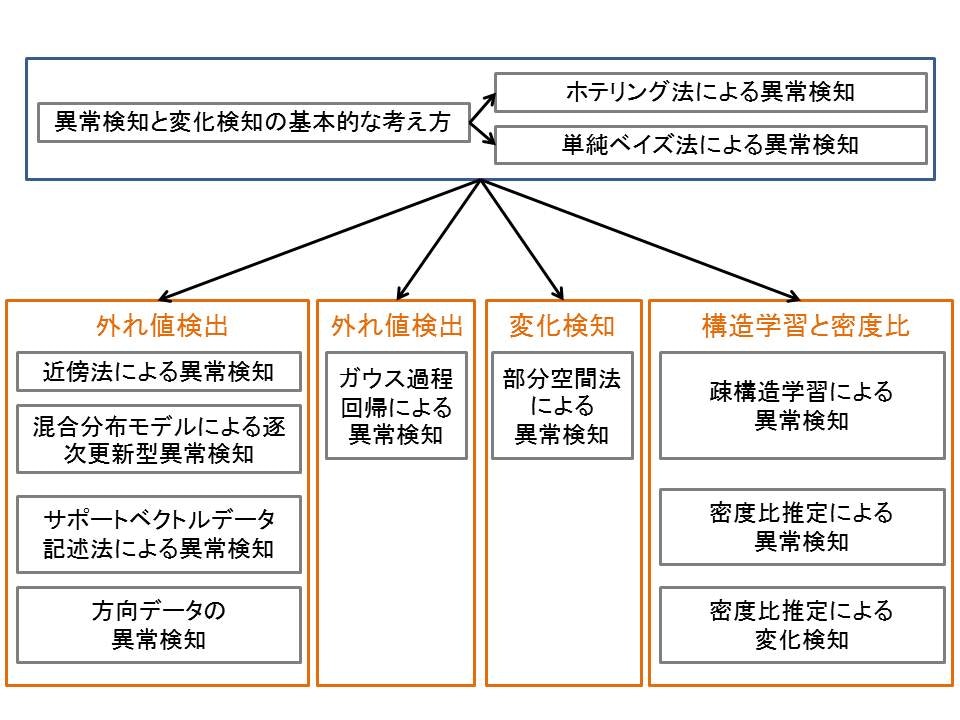
異常検知と変化検知の基本的な考え方
ホテリング法による異常検知
単純ベイズ法による異常検知

##シーンに応じた異常検知の手法を把握したい

近傍法による異常検知
混合分布モデルによつ逐次更新型異常検知
サポートべクトルデータ記述法による異常検知
方向データの異常検知
ガウス過程回帰による異常検知
部分空間法による異常検知
疎構造学習による異常検知

#最新の最適化手法まで抑えたい

密度比推定による異常検知
密度比推定による変化検知

全体像

上側の基礎を基に応用範囲について説明していきます。

#異常検知と変化検知の基本的な考え方

異常検知は異常な値を観測した瞬間に異常を検知して欲しいものですが、そのためには正常なデータが何かを把握する必要があります。
正常なデータがどのように表れるかを把握すれば、異常なデータはそれとは異なるようなデータであれば異常と判断できます。
では正常なデータはどのように判断すれば良いでしょう。

ここで使う考え方が確率分布です。確率分布を把握するとすべてのデータを把握しなくても正常なデータが取りうるだろう値を予測できる点が良い点です。

確率分布の良さはデータをもっとも良く表す確率分布を推定することが出来れば、データの推定は容易になります。
全てのデータに対して推定する必要がなく、確率分布の推定さえできれば良いということが利点です。

##確率分布の推定精度を測る指標

正常標本精度：正常のデータ当てれた精度

異常標本精度：異常なデータを当てれた精度

上記のバランスを取った値がF値といわれる値です。

F値：正常標本精度と異常標本精度の調和平均
（ROC曲線で調査することもある）

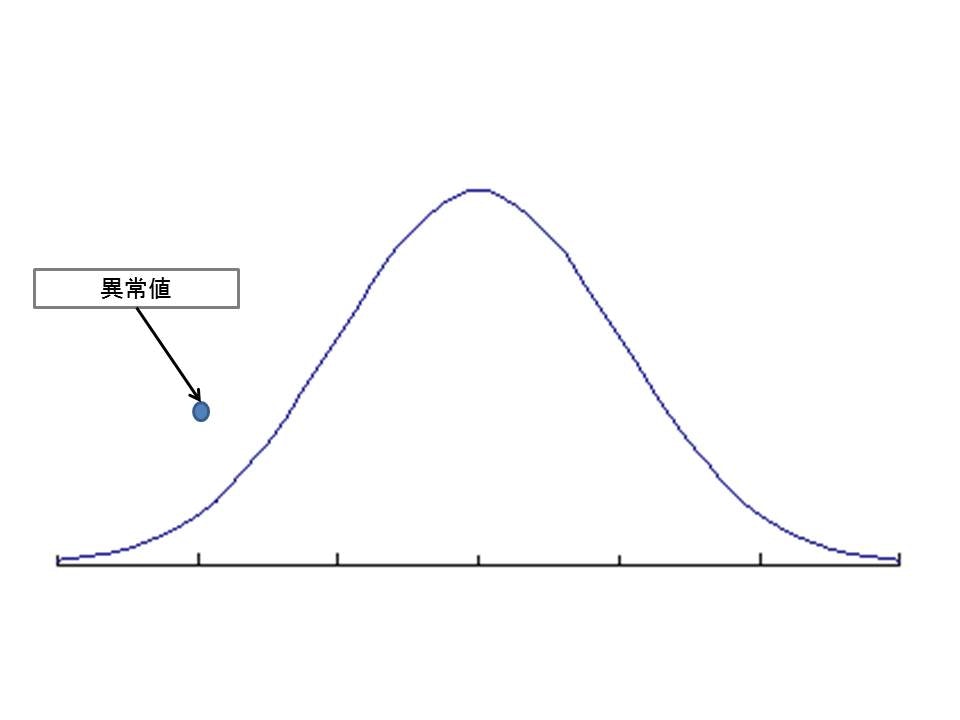
下記の例だと極端ですが、データが正規分布に従うと仮定して、異常値が検出された場合に把握できることが分かると思います。

#ホテリング法による異常検知

##利用シーン

データが多変量正規分布に従う時（ランダムなデータなど）の異常度検出の方法。
この多変量正規分布を最尤推定し、（平均と分散を推定する）得られたデータとのマハラノビス距離を計算することで一定の距離以上離れたものは異常と判断する手法。

##理由：
マハラノビス距離はデータのばらつきに左右されない距離なので、ばらつきの多いデータの異常度を測るときに有効。
ただしマハラノビス距離はカイ2乗分布に従うため、カイ2乗分布に当てはめて問題を解く必要がある。

#単純ベイズ法による異常検知

##利用シーン

変数が多い場合に変数切り分けて問題を解く手法がナイーブベイズです。

例えば迷惑メールフィルタの場合

迷惑メールになる要素が

1:リンクが多い
2:文章が異常に長い
3:画像が貼ってある
4:文章に適切でない単語が含まれる。（単語の数文だけ0と1で表される次元）
：

##理由
次元数が多い場合に各次元が独立だと仮定し、ベイズの決定則を使用すれば1次元の問題に変換して最尤推定が可能になる。

独立と仮定すると共分散の非対角成分が0とおいたものを扱えるので単純な平均と分散を計算する問題にラベルなしデータでも扱える。

##多項分布

###利用シーン
想定する分布が正規分布ではない場合

・各商品の閲覧回数
・各ジャンルの本の貸出回数

頻度専用の分布として多項分布で問題を解く場合も同様に独立として考えることができます。
ただし一度も表れないケースも考慮に入れる必要があるためスムージングと呼ばれる処理が行われています。

多項分布を推定するときに事前知識を考慮する事前分布のパラメータを使用する。この時の事前分布はディリクレ分布でベイズの定理を用いて事後確率を推定する。

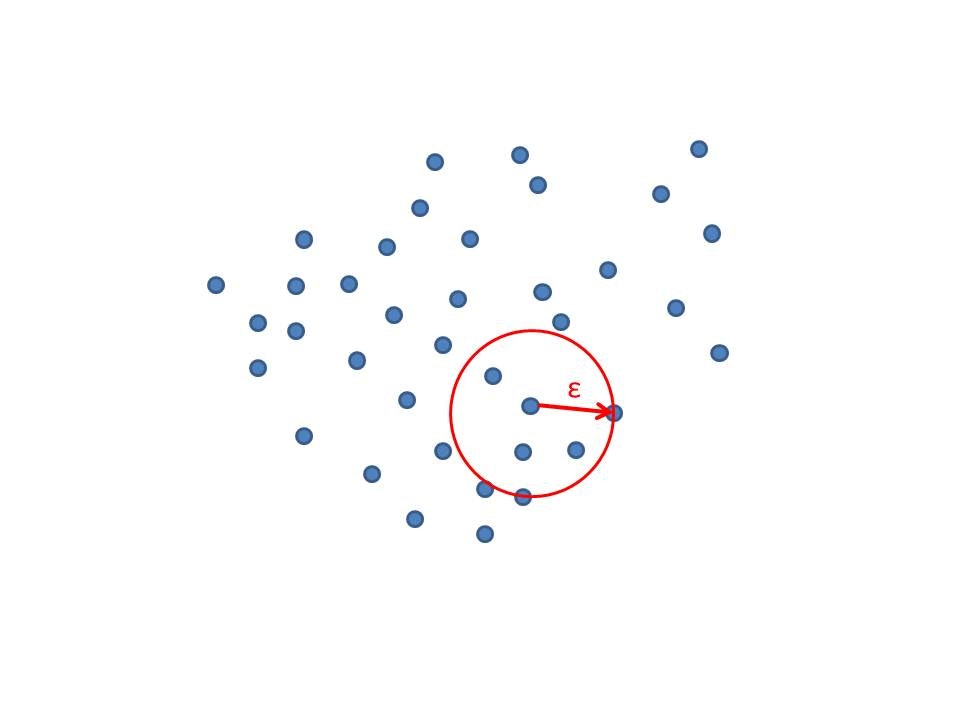
#近傍法による異常検知

##利用シーン
ホテリングの手法が有効なのはデータが一定値の周りに集中しているような状況のみです。
そのような制約がない手法として、近傍法があります。

下図のように近傍を取る点を与えてその半径εが大きい点を取るようなデータは異常度を疑う手法。

##手法
kの初期値に依存するため、半径εの設定はユークリッド距離で設定されています。
距離が適切でない場合は局所はずれ値度という手法が用いられます。

##マージン最大化近傍法

###利用シーン
ユークリッド距離の変わりに行列Aを半正定値行列と見立てて、データから学習することでより性能が向上できます。
分類したいグループとそうでないグループのマージンを最大化する手法をとるともっとも識別能力が上がるのでこの手法が使用されます。

##手法
最適化の手法には劣勾配と固有値計算が組み合わされて使用されます。

劣勾配とは通常の微分では計算できないような角の部分だけ正の項を入力して後は外す手法です。

固有値計算は変換する行列を固有値分解して負の固有値を0で置き換えることです。

確率モデルでも、データの近傍にしかデータが発生しないという定理の元に成り立ちます。

#混合分布モデルによつ逐次更新型異常検知

##利用シーン
実データはいろんな状態を含んだモデルが多く存在します。例えば発汗量と消費カロリーの関係性では運動時と平常時では観測される値が異なることが直観的もわかると思います。
混合分布モデルによる逐次更新型異常検知は直観を異なる複数のモードを持つ系の列にしたものであります。

##手法
EM法を用いて最適化（解析的に求まらないため）

最適化の手法には逐次更新とバッチ更新があります（逐次更新の場合は忘却率を用意して、過去の値を引きづりすぎないようにします）

#サポートべクトルデータ記述法による異常検知

##利用シーン

異常と正常を分けているベクトルは少数でそれはサポートベクトルと呼ばれる。
カーネルトリックを用いて、複雑な最適化問題を簡単な問題にしたい場合に使用する。

##手法

双対問題で問題を解きやすい形に置き換えて、カーネルトリックにより別の次元で単純な分類できる問題に置き換えて、サポートベクトルと呼ばれる識別面のみをよく表すベクトルで異常度を検知する手法です。
注意点として、カーネルトリックによる別空間への写像は特殊なテクニックでパラメータに依存するので確認してから使用が必要です。

#方向データの異常検知

##利用シーン
長さが揃っているデータで方向が異なるもの扱う分布を使用します。（大量の文書における各文書の単語の頻度ベクトルを規格化した場合など）

##手法
フォンミーゼス・フィッシャー分布（平均方向と集中度のパラメータを持つ）
方向データに対して有効な分布
異常度のカイ2乗分布により異常と検知する。

#ガウス過程回帰による異常検知

##利用シーン
入力と出力を観測して応答異常検知が可能なためシーンで使用します。

##手法
観測モデルと滑らかさを制御するモデルの２つで構成されます。

観測モデル
＊正規分布を考慮して、ノイズを含んだ予測を行います。
滑らかさを制御するモデル
＊正規分布で分散がデータの類似度を表します。

予測までのステップ

１：データの分布を求めます
２：データの分布と事前分布から事後分布を求めます
３：予測分布を求めます

予測分布はリッジ回帰にカーネルトリックを適用したものです

#部分空間法による異常検知

##利用シーン
変化が起こるが正常時のモデルと異常時のモデルが明らかに異なる場合のケースです。

##手法
正常状態の正規分布と異常状態の正規分布の比率で異常を検知します。
局所的な値で異常を検知せずに累積統計量を用いて、境界の値を超えているかどうかを検知します。
集約窓を使用して統計量を算出し、異常がないかどうかを検出します。

##特異スペクトル変換

###利用シーン
フォンゼス・フィッシャー分布を使用することで方向データを扱えるので、ノイズに強くなる利点があるため、部分空間でも特にノイズが多い場合に使用します。

###手法
フォンゼス・フィッシャー分布を使用して、部分空間同士の距離を評価することで変化度を計算する手法です。
特異値分解を行うことによってノイズ除去と同等の効果を発揮させます。

固有値分解をスペクトル分解と呼ぶ所に由来します。

計算量が多いのでランチョス法で計算量の改善は行います。

#疎構造学習による異常検知

##利用シーン

多変量の変数で表される観測業務で使用

各変数間の関係性に着目して、その変数の寄与度合を予測します。

直接相関と間接相関を区別して、行わないと相関関係のないものも相関関係があると勘違いしてしまいます。

例として”教会と殺人のパラドックス”があります。
教会の数と殺人の数に正の相関が見られたことです。
これは都市の人工という変数を介して相関が出た例ですが、明らかに適切でないことが予想できます。

##手法

1：多変量正規分布を用いて、各変数間の関係性を表す。これによってすべての変数のペアを考える必要がなくなり、期待値と共分散のみでデータを表すことで可能になります。
2：この多変量正規分布の精度行列を求めれば、変数間の相関関係が求まります。
3：今回、求めたい行列の前提としてノイズに強い疎な行列を前提にします。
4：その場合は疎な事前分布をもつラプラス分布を事前分布として、最大事後確率推定により、精度行列を推定する方がよいです。
5：行列の最適化の場合はブロック座標降下法を使用して、変数を一塊として最適化を行います。

###異常度計算時

あるデータが得られたときにそのデータと他のデータの条件付き確率を計算し、全体に対しての各値の異常度を計算

正常なデータと異常値を含むデータのカルバック・ライブラー・ダイバージェンス距離を計算します。

計算が少々ややこしいので密度比推定の手法が重宝されます。

#密度比推定による異常検知

この手法が強力な点はノイズに左右されづらく、応用範囲が広い点です。概念としては直接値を推定せずに密度比を推定するので理解しづらい点がありますが、理解できるとその強力さに脱帽します。

##利用シーン
正常なデータをもとに異常なデータを含むであろうデータの中から異常データを検出する時
個々のデータを見ずにデータ全体を見るため、個々のデータのノイズが載らずに精度が高くなる可能性があります。

##手法
カルバック・ライブラー密度比推定手法

１：密度比を表す基本モデルとして線形モデルを仮定
２：線形モデルに使用するパラメータは密度比ともとの確率分布の情報理論的距離（カルバック・ライブラーダイバージェンス）が近くなるように推定

最小化手法：最小2乗密度比推定法

#密度比推定による変化検知

##利用シーン
カルバック・ライブラーダイバージェンスではノイズの影響を受けやすい。特に構造学習においては個々の値のノイズが全体に影響してしまう。
センサデータなどのノイズが不可避なデータに対して、分布変化検知問題を解くには別の尺度が必要です。

##手法

ピアソン・ダイバージェンス：対数関数を含まないため、カルバック・ライブラーダイバージェンスよりも異常値にロバスト（変化に強い）
相対ピアソン・ダイバージェンス：異常値に関する感度とロバスト性をコントロールする関数があるため、用途によって調整可能です。

構造変化検知でも、一つ一つの値を導出するとノイズがのり、精緻な推定が難しいため、正確なデータの精度行列と異常値を含むデータの精度行列の差を取って、カルバック・ライブラーダイバージェンスを用いて、密度比を直接推定します。

#参考

統計処理ソフトウェアRについてのTips
http://minato.sip21c.org/swtips/R.html

多項分布
http://www.weblio.jp/content/%E5%A4%9A%E9%A0%85%E5%88%86%E5%B8%83

「異常検知と変化検知」
http://www.amazon.co.jp/dp/4061529080?_encoding=UTF8&isInIframe=0&n=465392&ref_=dp_proddesc_0&s=books&showDetailProductDesc=1#product-description_feature_div