ドコモ先進技術研究所アドベントカレンダー17日目の記事です。
はじめまして。ドコモ2年目社員の泉澤です。
配属当初の業務は主に5G時代コアネットワークやスタジアム向けWi-Fiの技術に関する研究開発に携わってきましたが、
今年の夏から新たな試みとして、“マルチエージェントシミュレーション(MAS)による制度設計”について研究を進めています。
「こんなことやっているよ」という研究紹介と共に、有識者の方々からコメントを頂けたら嬉しいなという想いから、私も執筆してみることにしました。
今回執筆する内容は、先週学会で発表させていただいた研究概要となります。
内容としては「どんなルールを作れば人々が協力し会える社会は生まれるのか」について、進化ゲーム理論に基づくMASを実装することにより検討していきます。
その中でも、シェアリングエコノミーにおけるC2Cサービスに焦点を当てて書き進めていきたいと思います。
そもそもシェアリングエコノミーって何?
シェアリングエコノミーとは、個人が持て余している遊休資産を他の個人も利用可能にする経済活動の総称です。
ちょっと何言ってるか分かりませんね。
これまで、モノの売り買いを行う相手は、企業などの法人が一般的でした。しかし近年、モノの売り買いは法人だけでなく、一般の個人同士で行われることが増えてきています。
(Airb○bやU○erと聞けば、ピンと来る方もいるかもしれませんね)
シェアリングエコノミーにおけるサービス(C2Cサービス)では、自身の遊休資産を提供する個人(提供者)と、その遊休資産を利用する個人(利用者)との間で取引が行われるのが特徴です。
この遊休資産には、居住空間やモノ、カネのような目に見える有形の資産だけでなく、人の時間やスキルなど目に見えない無形の資産をも含んでいます。

ビジネスモデルの例として、C2Cサービス事業者の多くは、提供者と利用者とをマッチングさせ、個人間の取引で生じた金銭の一部を手数料として徴収することにより収益を獲得しています。
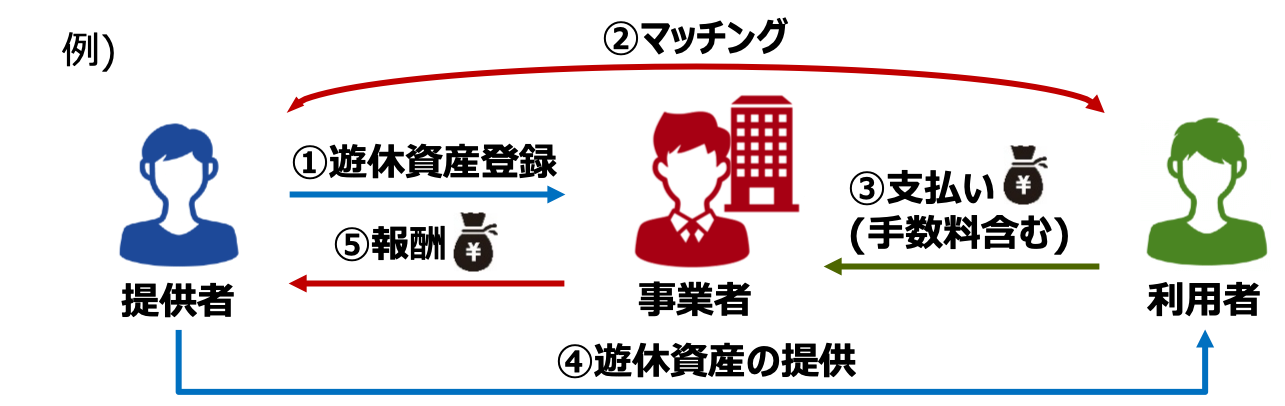
近年、スマートフォンの普及やSNSの発達により、提供者と利用者とのマッチングが容易になったことから、C2Cサービスの市場は世界的に拡大しています。
これによって、シェアリングエコノミーは”就業機会の創出”、”環境負荷の低減”、”消費者利益の増加”など、様々な経済的・社会的効果をもたらす活動して世界的に注目されているといえるでしょう。

C2Cサービスの課題
しかし、C2Cサービスの発展とともに、個人同士のトラブルは急増しています。このトラブルは提供者と利用者の両者が原因を生み出しているんですね。
前者の例では、利用者の期待に反して粗悪な資産が提供されることなどがあります。
また後者の例では、提供者の意向に反して利用者が資産を損傷や盗難、紛失してしまうことなどが挙げられます。
これらの原因の共通点は、取引相手の意向に反して不誠実な行動を取る個人が存在することです。
したがって、C2Cサービス事業者が事業による収入を増加させるためには、市場に誠実な行動を取る個人を増やすことでトラブルを減らし、提供者と利用者の両者に対して安心安全な取引を担保する必要があります。
C2Cサービス事業者が導入する相互評価制度
C2Cサービス事業者の多くは、個人間のトラブルを未然に防ぐため、相互評価制度を導入しています。
相互評価制度とは、個人同士の取引を終了する毎に提供者と利用者が互いの対応について主観的評価を行う制度です。一般的に、5段階評価による評価付けを行う方法が多く採用されていますね。

相互評価が蓄積されると、個人は取引を行う前に相手の性格や取引における応対品質、あるいは提供される資産の品質や資産の扱い方など、取引を行う上で重要となる相手が誠実な行動を取るかどうかを窺い知ることができます。
これにより、低い評価点がつけられている個人との取引を避けることで、起こりうるトラブルを未然に回避することが可能です。
このような相互評価制度の導入によって、個人は誠実な取引相手を予測することができます。しかし現状、個人間のトラブルは未だに存在します。
これは、自身の評価内容に捉われず不誠実な行動を取り続ける個人が一部存在するためです。
そのため、より安心安全なC2Cサービスを提供するためには、相互評価制度に加え、相手の意向に沿って誠実な行動を取らせる制度設計を行う必要があります。
今回のアプローチ方針
安心安全なC2Cサービスの実現に向けて、事業者は制度設計にコスト(予算)をかければかけるほど誠実な行動を取る個人が増えることは明らかです。
(極端な話、「サービスを誠実に利用してくれたら、100億円あげちゃう」って言われたら「よし、ちゃんとルールを守ってみるか!」となりますよね)
しかし、事業者にも制度設計にかけられるコストには上限があるわけです。
このことから、事業者がサービスにかけるコストと誠実な行動を取る個人の割合との間にはトレードオフの関係にあることがわかります。

そのため、今回はC2Cサービスにおける誠実な個人の増加に向けた制度設計を、進化ゲーム理論に基づくマルチエージェントシミュレーションを用いて実装し、誠実な個人の増減におけるパラメータ閾値を明らかにしていきます。
そのまえに、進化ゲーム理論って何?
社会環境下における人々の意思決定はとても複雑です。
例えば、常に学習し続けて自身の利益を最大化させようとする個人がいたり、一方で、将来のことを全く鑑みずに直近のことばかり考える個人や、長年の勘を頼りに行動を変えようとしない個人、突然デタラメな行動を取る個人がいたりなど、世の中には様々な意思決定が存在します。
進化ゲーム理論は、このような考えに基づいて、時間の経過とともに個人が定常的に取る/淘汰される意思決定(戦略)を学習し、最終的に生き残っていく戦略を探る方法論です。
もともと、進化ゲーム理論は生物の進化を解析するために進化生物学へ取り組まれた学術分野でしたが、今では社会学や経済学などの諸分野に応用され盛んに研究が行われています。
ゲームの定義
今回は、C2Cサービスで起こり得る社会経済現象について関連研究を元にゲームを定義していきます。
C2Cサービスにおける人々は、個人間取引に向けて以下の4戦略から選択可能とします。
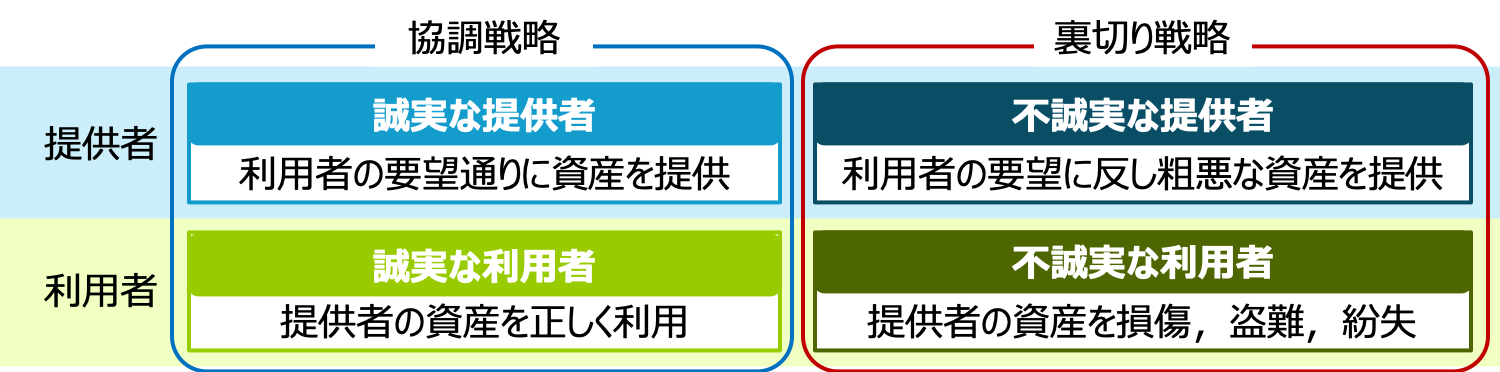
■ 協調戦略
- 誠実な提供者
利用者の要望通りに資産を提供する誠実な提供者
- 誠実な利用者
提供者の意向に沿って正しく資産を利用する誠実な利用者
■ 裏切り戦略
- 不誠実な提供者
利用者の要望に反してサービス品質が著しく低い資産を提供する不誠実な提供者
- 不誠実な利用者
提供者の意向に反して資産を損傷や盗難、紛失などを行う不誠実な利用者
C2Cサービスにおける提供者と利用者は、個人間取引時に取った戦略に応じて利得を獲得します。
今回定義するゲームの利得構造は以下のように設定しました。
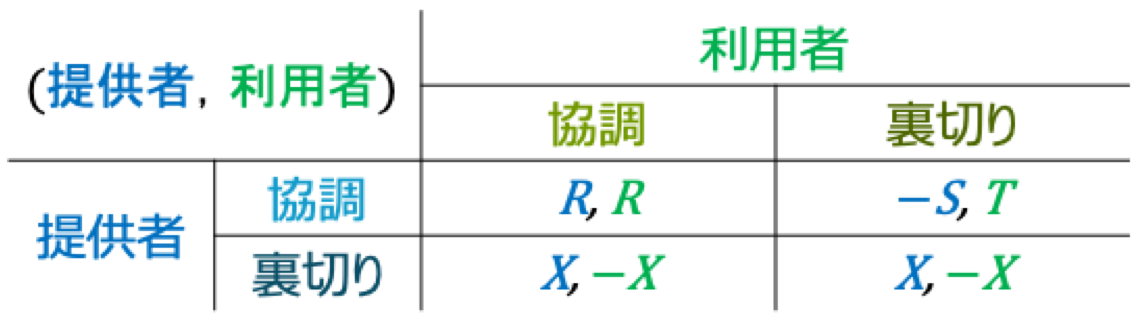
利得構造における青色の利得は提供者が獲得し、緑色の利得は利用者が獲得します。
各利得の関係性は以下のように示されます。
$$ 2R>T>R>S>X≧0 $$
この利得構造で…
■ 提供者と利用者の双方が協調戦略を取った場合
両者は誠実に取引を行おうとするので、提供者と利用者の双方は報酬Rを獲得します。
■ 提供者が協調戦略を、利用者が裏切り戦略を取った場合
提供者は、自身の資産を利用者によって損傷や盗難、紛失されてしまうため、獲得する利得が負の値となります。
利用者は、提供者の資産を自由気ままに利用するので、本来の報酬R以上の利得Tを獲得します。
■ 提供者が裏切り戦略を取った場合
提供者は、利用者の戦略に左右されずに粗悪な資産を提供します。そのため、利用者はどちらの戦略を取ろうと期待に沿った資産を利用することができないので、獲得する利得が負の値となります。
今回のシミュレーションでは、利得Tを1.0、利得Sを0.5、利得Xを0.25に設定してみました。
今回考える制度設計について
C2Cサービスを行う個人らに誠実な行動(協調戦略)を取らせる制度設計を考えます。
今回は、各個人の評価内容に応じて変化するインセンティブもしくはペナルティを個人に付与する制度設計を検討してみます。
具体的に説明すると
評価点の高い個人は、本来の取引報酬Rに加えて、取引相手との評価点に応じたインセンティブを獲得します。
対して、評価点の低い個人は、本来の取引報酬Rから取引相手との評価点さに応じたペナルティが引き去られていくという内容です。
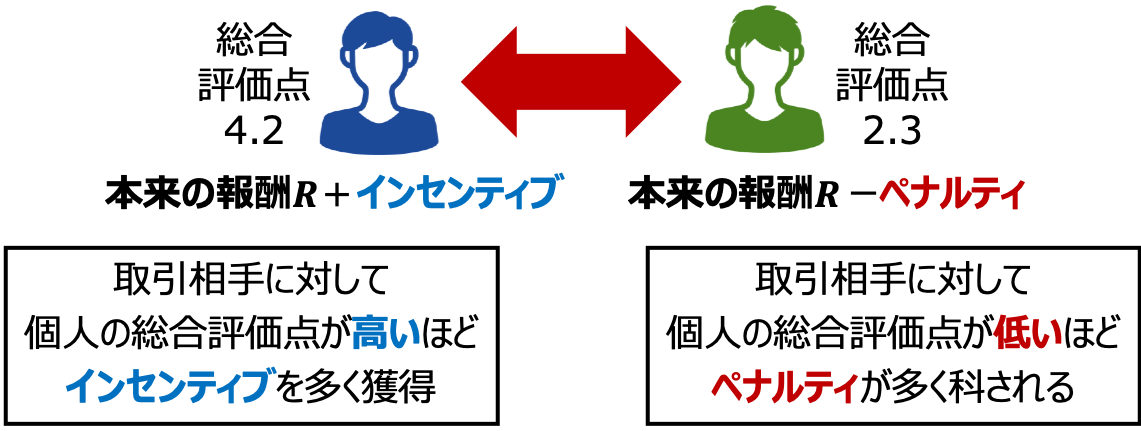
本制度において、ある個人iが獲得する報酬*Ri*は以下に示します。
R_i = \left\{
\begin{array}{ll}
R\biggl[1+\alpha_{Gain}\biggr(\frac{|Rep_i-Rep_j|}{Rep_{max}-Rep_{min}}\biggr)\biggr] & (Rep_i \geqq Rep_j) \\
R\biggr[1-\alpha_{Loss}\biggr(\frac{|Rep_i-Rep_j|}{Rep_{max}-Rep_{min}}\biggr)\biggr] & (Rep_i \lt Rep_j)
\end{array}
\right.
ここで、αGainとαLossは付与するインセンティブおよびペナルティを決定する重み付け係数を表し、RepiとRepjはそれぞれ個人iと取引相手jが持つ総合評価点です。
また、*RepmaxとRepmin*はそれぞれ最大と最小の評価点を表しています。今回のシミュレーションでは5段階評価による相互評価を採用するため、Repmax=5、Repmin=1とします。
先ほど述べた利得構造でRとしていた報酬を各個人の評価点に基づくRiとして利得の計算を行なっていきます。
今回のシミュレーションでは、本来の取引報酬であるRと、インセンティブおよびペナルティを決定する重み付け係数*RepiとRepj*をそれぞれ可変させて評価を行います。
マルチエージェントシミュレーションとは?
それでは、これまで説明してきたゲームの定義および今回の制度設計に基づいて、マルチエージェントシミュレーションの実装を行うことにより、起こりうる社会経済現象を評価していきます。
説明が遅くなっていましましたね。マルチエージェントシミュレーションについてです。
マルチエージェントシミュレーション、通称MASとは、ある社会環境下における個人らの意思決定を模擬するエージェントを仮想空間上に多数配置し、エージェント同士の関わり合いによって創発される社会経済現象をシミュレートしていく手法です。

このMASにより実装した社会環境下で、各エージェントは自身の利得を最大化する戦略(今回の場合は協調戦略または裏切り戦略)のどちらを取るかを学習し、個人間取引を繰り返し行った後に、最終的に生き残る戦略を決定します。
シミュレーションの流れ
シミュレーションの流れは次の通りです。
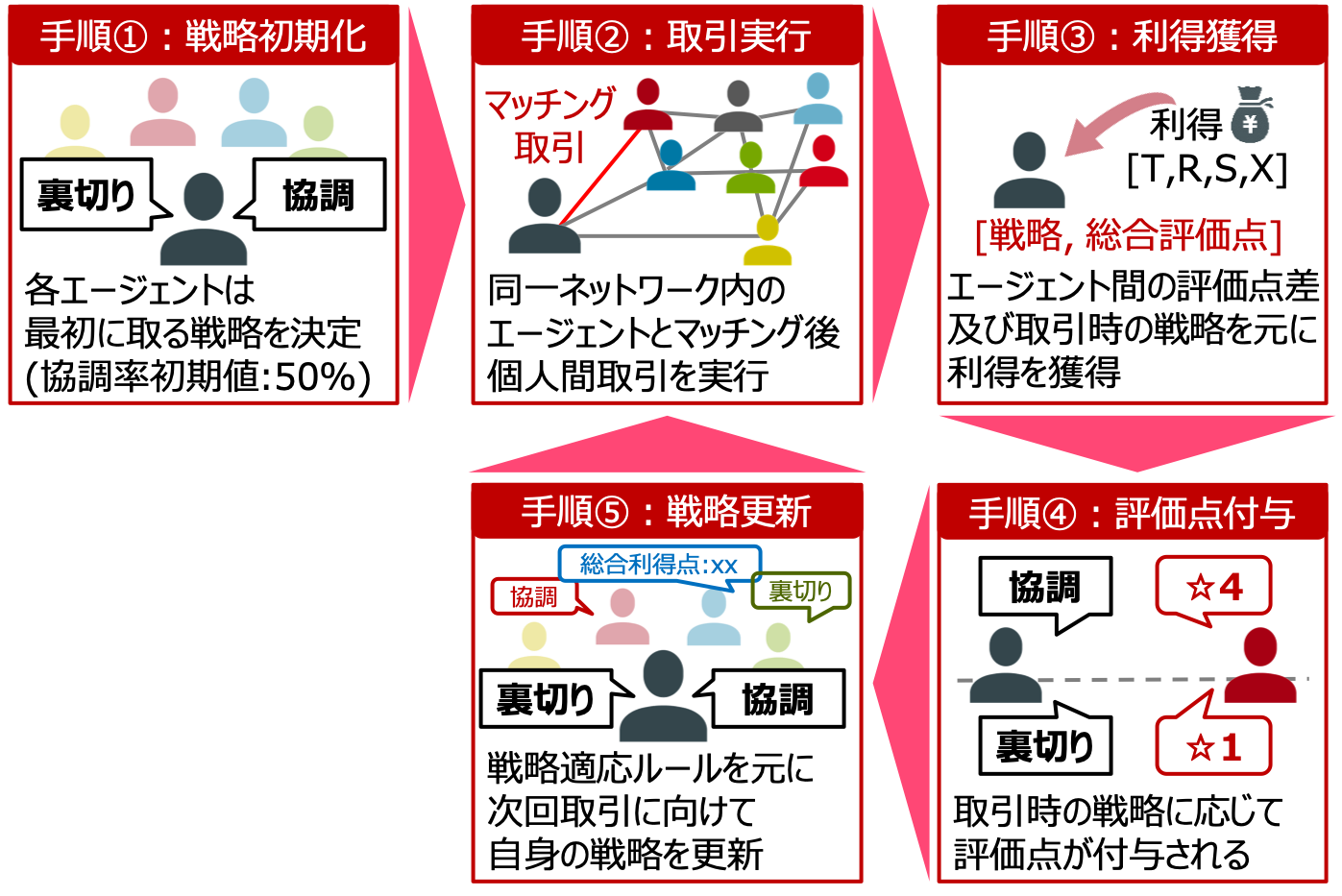
■手順①:戦略初期化
まず、各エージェントは個人間取引に向けて、最初に取る戦略(協調or裏切り)を決定します。
今回は、協調戦略を取るエージェントの割合が50%となるように戦略をランダムに割り振っていきます。
■手順②:取引実行
エージェントは、同じネットワーク内でリンクされた隣人らの中から取引相手を一人ランダムで選択し、提供者もしくは利用者として個人間取引を行います。
■手順③:利得獲得
取引終了後、エージェントは自身と取引相手の戦略と総合評価点を元に利得を獲得します。
■手順④:評価点付与
利得獲得後、エージェントは取引時に取った戦略に基づき、取引相手から評価点を付与されます。
■手順⑤:戦略更新
最後に、エージェントは戦略適応ルールを元に、次回取引に向けて自身の戦略を変更するか決定します。
この手順②から⑤までを繰り返し行い、最終的に生き残る戦略を評価していきます。
評価環境
ネットワークモデル
ネットワークモデルは、複雑ネットワーク呼ばれる学術分野において、実世界の社会ネットワークを模擬するモデルとして知られるバラバシ・アルバートのスケールフリーモデルを採用しました。
このモデル上において、全エージェント数を100、平均次数を8と設定しています。
戦略適応ルール
先ほど説明した手順⑤における戦略適応ルールでは、Fermi関数のPairwise比較を採用しています。
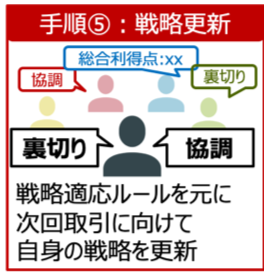
このモデルでは、上記のネットワークでリンクされたエージェントの中からランダムな隣人jを一人選択し、自身と相手の利得差に応じて、実際に隣人の戦略を模倣するか否かを決定するモデルです。
このモデルは以下の式で示されます。
P_{i←j} = \frac{1}{1+\exp\Bigl(\frac{\Pi_i-\Pi_j}{\kappa}\Bigl)}\ [\mathrm{%}]
これは、あるエージェントiが隣人エージェントjの戦略を模倣する確率を表しています。ここで、Πはあるエージェントが獲得した累計利得を表しています。今回、温度係数*κは0.1に設定しました。
この式では、エージェントi*は累積利得が隣人エージェントの累積利得より下回っている程、隣人エージェントの戦略を模倣する確率が高くなることを表しています。
エージェントの戦略に応じた評価付け
手順4において、各エージェントは自身が取った戦略(協調or裏切り)に応じて、取引相手から評価点を以下の確率で付与されるものとします。
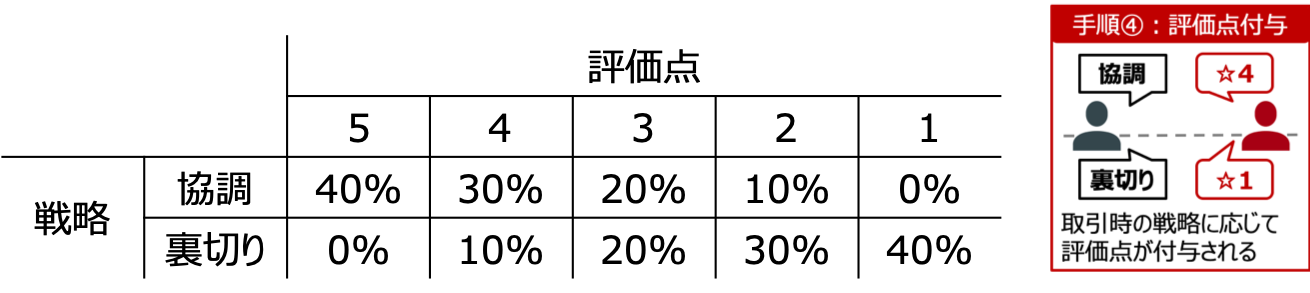
エージェントの取引実行率
先ほど説明した手順②において、本評価では、個人が取引相手の評価点を元に取引を行うか否かを意思決定する選択バイアスを設定します。
具体的には、個人らは取引相手の評価点が高いほど取引に応じる確率が高くなり、対して、取引相手の評価点が低いほど取引を行う確率が低くなります。
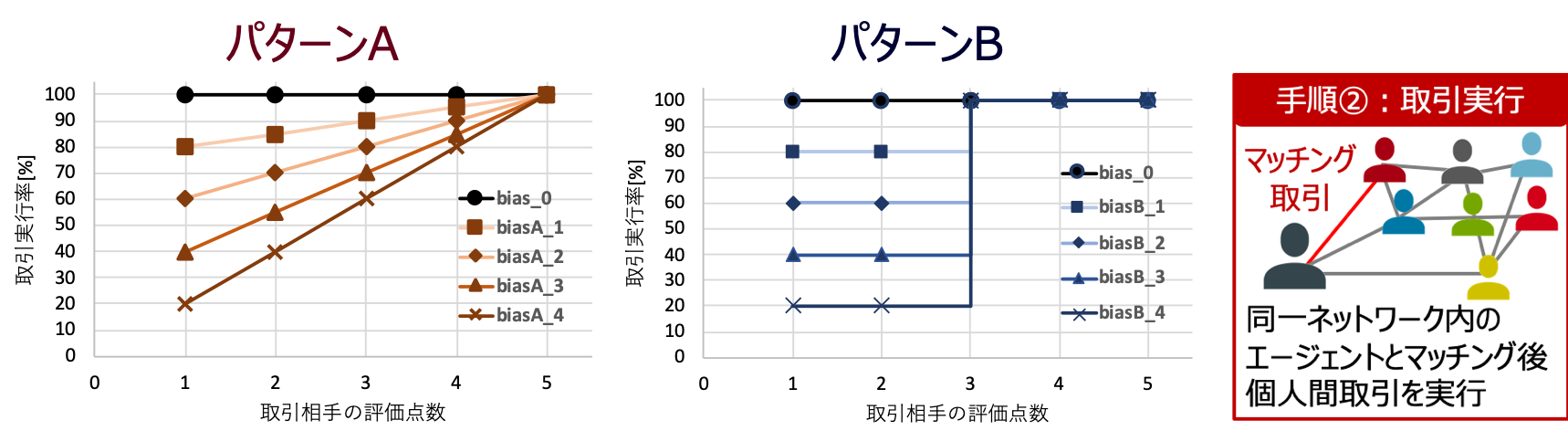
今回は、取引実行率が線形に変化するパターンAと、評価点3を閾値に取引実行率がステップ状に変化するパターンBを用意します。
選択バイアスがない、つまり相手の評価点に左右されずに必ず取引を実行するシナリオと、
各パターンにおいて取引実行率が異なる4通りのシナリオをそれぞれ評価していきます。
評価結果
選択バイアスが無の場合
選択バイアスが無い場合、本来の報酬Rの値を0.9としたときの**協調率(協調戦略を取る個人の割合)**を表す結果は以下のようになりました。
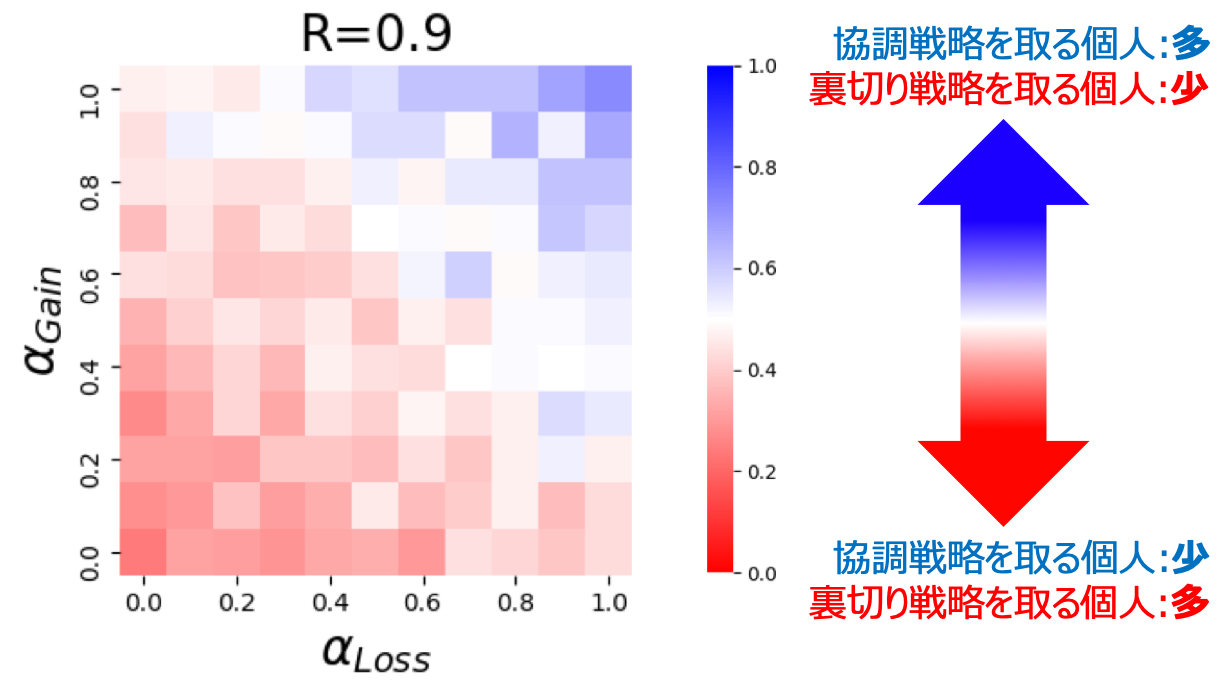
このとき、横軸はαLossを、縦軸はαGainを表し、それぞれ0から1まで0.1刻みに変化させた際の協調率を示します。
この図では、各利得のパラメータが表す領域が青いほど協調率を取る個人の数が多くなり、領域が赤いほど裏切り戦略を取る個人が多くなることを表しています。
選択バイアス有との比較
次は、本来の報酬Rが0.8および0.9の場合の利得パラメータに応じた協調率について、選択バイアスがある場合とない場合との結果を比較します。
次の結果では、選択バイアスがない場合シナリオと、各パターンでバイアスが最も顕著なシナリオをピックアップしています。
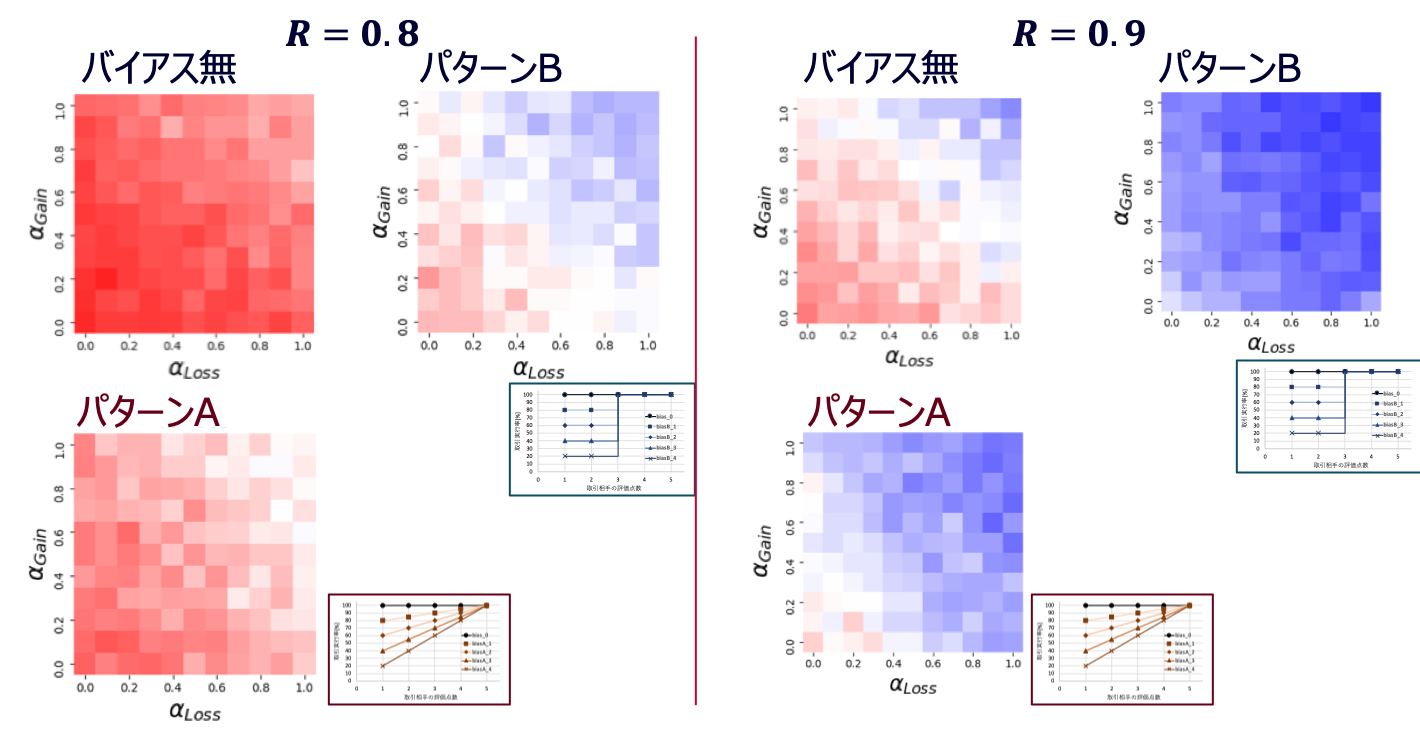
選択バイアスの有無を比較すると、選択バイアスが生じることによって青い領域は拡大していることがわかるかと思います。
このことから、裏切り戦略を取る個人は取引実行率が低下するため、協調戦略を取る個人の数は増加することが推察されます。
つまり、裏切り戦略を取る個人は、取引を行う機会が失われると利得を増やすことができなくなるため、獲得する利得の大小に関わらず協調戦略を取る必要があると学習していくことが考えるられるわけです。
そのため、C2Cサービス事業者は、評価点の低い個人に対して取引を行わせづらくさせる仕組みを導入することで、個人に支払うコストを抑えつつ協調戦略を取る個人を増加可能であることが示唆されます。
所望の協調率を達成する利得パラメータ条件
次は、所望とする協調率(協調戦略を取る個人の割合)を満たすために必要な各利得パラメータ条件を確認するため、先ほどの結果を元に線形回帰分析を行います。
今回の分析では、所望とする協調率を**50%とし、必要な各利得パラメータ条件を確認しました。
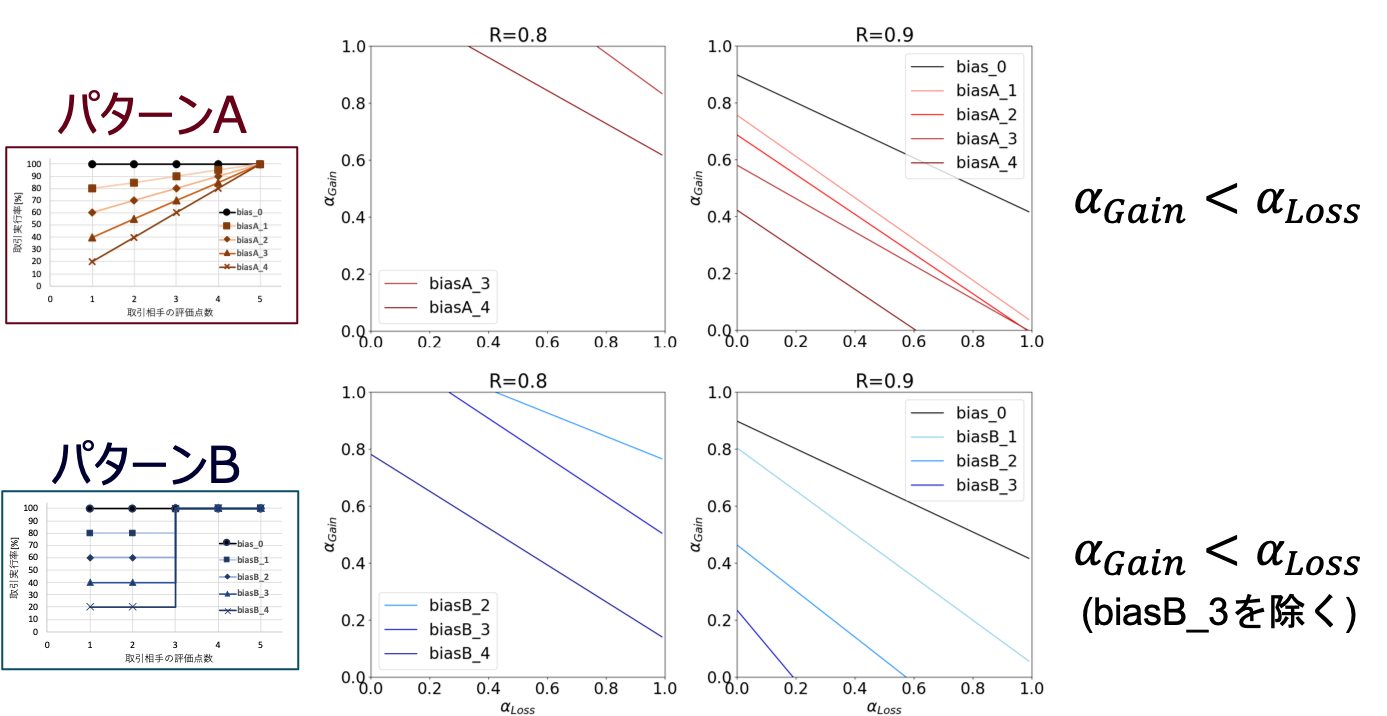
協調率50%**を達成する各パラメータはシナリオ毎に異なり、選択バイアスが強く働くほど必要となる各パラメータの値は小さくなっていますね。
また、グラフの傾きに着目すると、例外を除く全てのシナリオでは、*αGainよりもαLoss*の方が、必要な利得パラメータの値が大きくなっていることがわかります。
つまり、C2Cサービスを行う個人は、ペナルティを課されることよりもインセンティブを付与されることを動機付けとし、協調戦略を取る傾向があると推察することができます。
終わりに
進化ゲーム理論に基づくマルチエージェントシミュレーションは、ある制度を施すと人々がどのように行動するのかを評価するのに適していますが、モデルの構築についてまだまだ課題の多い技術手法です。
今回はシミュレーション上の評価を行いましたが、実世界での社会実験もやってみたいですね。
ここまで、この記事をご覧いただいた皆様に感謝申し上げます。